【数据结构】图的广度优先遍历
一.广度优先遍历的基本思想
(1)访问顶点v;
(2)依次访问v的各个未被访问的邻接点v1,v2,v3……,vk;
(3)分别从v1,v2,v3……,vk出发依次访问他们未被访问的邻接点,并使“先被访问顶点的邻接点”先于“后被访问的邻接点”被访问。直至图中所有与顶点v有路径相通的顶点都被访问到。
二.广度优先遍历的伪代码
1.初始化队列Q;
2.访问顶点v;visited[v]=true;顶点v入队列Q;
3.while(队列Q非空)
3.1 v=队列Q的队头元素出队;
3.2 w=顶点v的第一个邻接点;
3.3while(w存在)
3.3.1 如果w未被访问,则访问顶点w;visited[w]=1;顶点w入队;
3.3.2 w=顶点v的下一个邻接点
三.代码实现
template<class T>
void MGraph<T>::BFSTraverse(int v){bool visited[vertexNum]=false;queue<int> Q;int w,i=0,count=0;cout<<vertex[v]<<endl;visited[v]=true;++count;Q.push(v);if(count==vertexNum){return;}while(!Q.empty()){v=Q.front();//队头元素出队Q.pop();for(i=0;i<vertexNum;i++){if(arc[v][i]&&!visited[i]){//w未被访问w=i;cout<<vertex[w]<<endl;visited[w]=true;++count;Q.push(w);}}}}template <class T>
void ALGraph<T>::BFSTraverse(int v){bool visited[vertexNum]=false;queue<int> Q;int w,i=0,count=0;cout<<adjList[v].vertex<<endl;visited[v]=true;++count;Q.push(v);if(count==vertexNum){return;}while(!Q.empty()){v=Q.front();//队头元素出队Q.pop();struct ArcNode *p=adjList[v].firstEdge;while(p){if(!visited[p->adjvex]){w=p->adjvex;cout<<adjList[w].vertex<<endl;visited[w]=true;++count;Q.push(w);}else{p=p->next;}}}
}
四.总结
广度优先:确定起始节点后,全部邻接点(分支)同时开始遍历;
深度优先:先从一个邻接点(分支)开始遍历,直至该分支全部遍历完成,再遍历按顺序的下一个分支。
相关文章:

【数据结构】图的广度优先遍历
一.广度优先遍历的基本思想 (1)访问顶点v; (2)依次访问v的各个未被访问的邻接点v1,v2,v3……,vk; (3)分别从v1,v2,v3……...

AM@函数展开成幂级数@间接法@常用麦克劳林幂级数展开公式
文章目录 间接法推导幂级数展开常用麦克劳林幂级数展开公式应用例例例 间接法推导幂级数展开 已知函数的幂级数展开公式间接推导其他函数幂级数 使用原始的推导公式推导函数的幂级数展开是繁琐不便的,需要分别计算各项系数 a n f ( n ) ( 0 ) n ! a_{n}\frac{f^{(n)}(0)}{n!}…...

LeetCode994.腐烂的橘子
看完题我觉得这不是和上一道岛屿的题一样简单嘛,然后写了将近2个小时才写出来,我的思路就是,用check()先对grid检查一下,是否有以下情况: (如果有1的周围都是空,则这个位置用不腐烂,…...
【开源】基于Vue和SpringBoot的康复中心管理系统
项目编号: S 056 ,文末获取源码。 \color{red}{项目编号:S056,文末获取源码。} 项目编号:S056,文末获取源码。 目录 一、摘要1.1 项目介绍1.2 项目录屏 二、功能模块2.1 普通用户模块2.2 护工模块2.3 管理员…...
【音视频基础】AVI文件格式
AVI文件采用的是RIFF文件结构方式。波形音频wave,MIDI和数字视频AVI都采用这种格式存储。 AVI文件的整体结构如下图所示 构造RIFF文件的基本单元叫做数据块(Chunk),每个数据块包含3个部分 4字节的数据块标记(或者叫…...
,剑指offer,力扣)
图书馆整理I(从尾到头打印列表),剑指offer,力扣
目录 题目地址: 我们直接看题解吧: 解题方法: 难度分析: 审题目事例提示: 解题思路(辅助栈): 代码(递归): 代码(列表插入): 相似题目对…...

C++编写的多线程自动爬虫程序
目录 引言 一、程序的设计 二、程序的实现 三、程序的测试 四、优化与改进 五、代码示例 总结 引言 随着互联网的快速发展,网络爬虫程序已经成为数据采集、信息处理的重要工具。C作为一种高效的编程语言,具有高效的并发处理能力和丰富的网络编程…...

SMB信息泄露的利用
一、背景 今天分享SMB信息泄露,SMB(Server Message Block)网络通信协议,早些时候被用于Web链接和客户端与服务器之间的信息通信,现在大部分Web页面使用HTTP协议,在web领域应用较少。另一方面SMB协议还是被…...
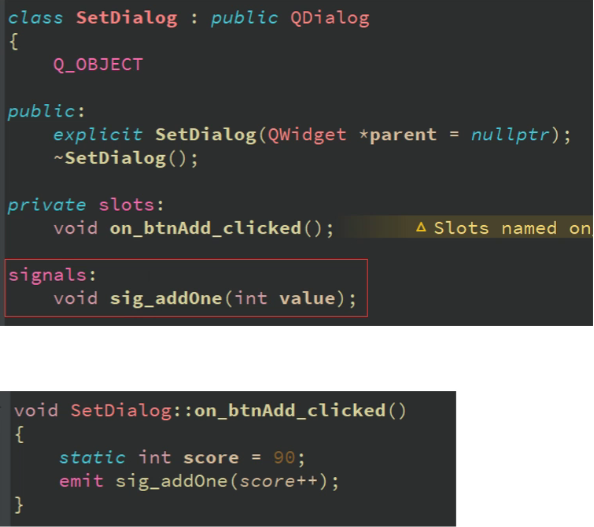
QT自定义信号,信号emit,信号参数注册
qt如何自定义信号 使用signals声明返回值是void在需要发送信号的地方使用 emit 信号名字(参数)进行发送 在需要链接的地方使用connect进行链接 ct进行链接...

06.webpack性能优化--构建速度
优化babel-loaderhappyPackIgnorePluginparalleUglifyPluginnoParse自动刷新 1 happypack多进程打包 js单线程,开启多进程打包提高构建速度(特别是多核CPU) const HappyPack require(happypack)module.exports smart(webpackCommonConf,…...

11-15 周三 softmax 回归学习
11-15 周三 softmax 回归学习 时间版本修改人描述2023年11月15日11:17:27V0.1宋全恒新建文档 简介 softmax分享可以参考什么是softmax 回归估计一个连续值,分类预测一个离散类别。 恶意软件的判断 回归和分类 分类可以认为从回归的单输出变成多输出 B站学习 softm…...

React新手必懂的知识点
react思想:组件化开发 React 的核心概念是组件化开发,将用户界面拆分成独立的可复用组件。学习如何创建和使用 React 组件,以及组件之间的数据传递和通信是非常重要的。 React的思想就是拆分组件与使用组件。 import React from react;// 定…...

es为什么这么快
es为什么这么快的方式 es的基于Lucene开源搜索引擎,负责文件存储和搜索,支持http请求,以json形式展示 这样介绍你有可能有点迷糊我们详细解释 es 使用的倒排索引的方式,进行数据存储方式,给每一个字段创建索引&…...
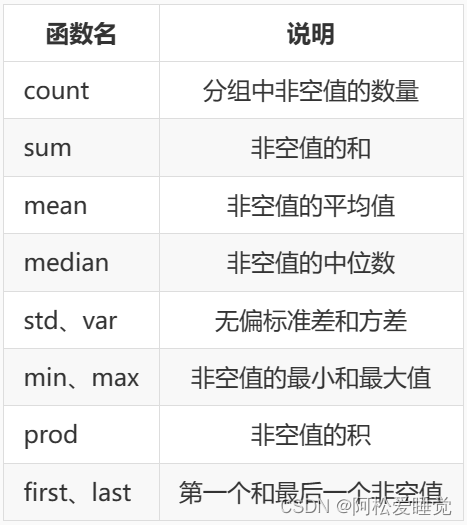
Pandas分组聚合_Python数据分析与可视化
Pandas分组聚合 分组单列和多列分组Series 系列分组通过数据类型或者字典分组获取单个分组对分组进行迭代 聚合应用单个聚合函数应用多个聚合函数自定义函数传入 agg() 中对不同的列使用不同的聚合函数 分组聚合的流程主要有三步: 分割步骤将 DataFrame 按照指定的…...
VMware17虚拟机Linux安装教程(详解附图,带VMware Workstation 17 Pro安装)
一、安装 VMware 附官方下载链接(VM 17 pro):https://download3.vmware.com/software/WKST-1701-WIN/VMware-workstation-full-17.0.1-21139696.exe 打开下载好的VMware Workstation 17 Pro安装包; 点击下一步; 勾选我…...
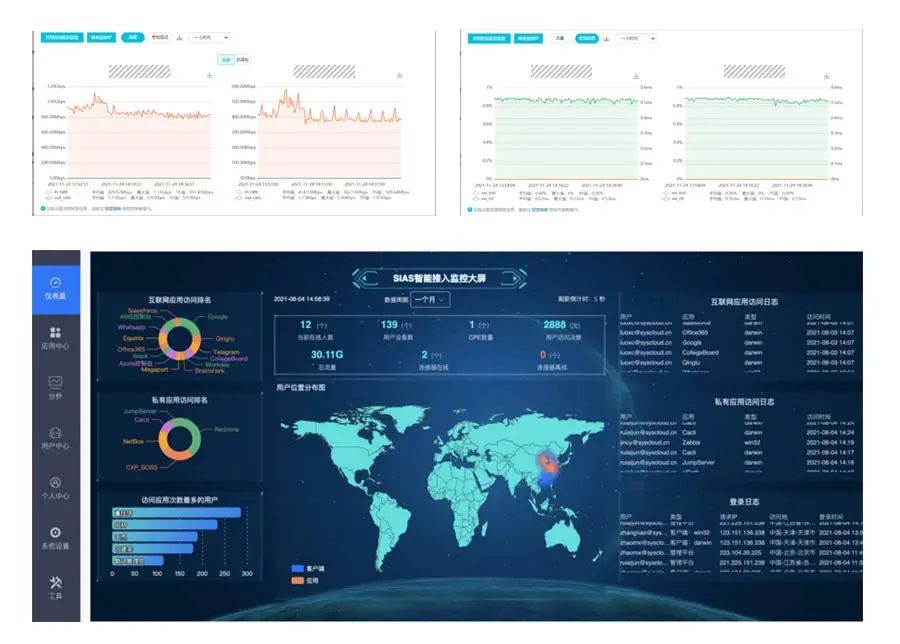
基于SDN技术构建多平面业务承载网络
随着企业数字化的浪潮席卷各个行业,传统网络架构面临着更为复杂和多样化的挑战。企业正在寻找一种全面适应数字化需求的网络解决方案。随着软件定义网络(SDN)的发展,“多业务SDN一张网”解决方案为企业提供了一种全新的网络架构&a…...
关于卓越服务的调研报告
NetSuite知识会发起的本次调研从2023年11月2日开始,到11月12日结束。16日已向参与调研的朋友邮件回复,感谢您的付出!今朝分享此报告,各位同学参考。 调研问题与反馈总结 问题1:您能想到哪些服务组织能够提供高满意度&…...

ubuntu22.04换源
1、系统信息 lsb_release -a No LSB modules are available. Distributor ID: Ubuntu Description: Ubuntu 22.04.3 LTS Release: 22.04 Codename: jammy2、进入 /etc/apt/ 目录: cd /etc/apt/ 3、备份默认源文件 sudo cp sources.list sources.list_bak 4、编…...
03. Python中的语句
1、前言 在《Python基础数据类型》一文中,我们了解了Python中的基础数据类型,今天我们继续了解下Python中的语句和函数。 2、语句 在Python中常用的语句可以大致分为两类:条件语句、循环语句。 2.1、条件语句 条件语句就是我们编码时常见…...
Linux CentOS7 添加网卡
一台主机中安装多块网卡,有许多优势。可以实现多项功能。 为了学习网卡参数的设置,可以为主机添加多块网卡。与添加磁盘一样,要在VMware中设置。利用图形化方式或命令行查看或设置网卡。本文仅初步讨论添加、查看与删除网卡,有关…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

Caliper 配置文件解析:fisco-bcos.json
config.yaml 文件 config.yaml 是 Caliper 的主配置文件,通常包含以下内容: test:name: fisco-bcos-test # 测试名称description: Performance test of FISCO-BCOS # 测试描述workers:type: local # 工作进程类型number: 5 # 工作进程数量monitor:type: - docker- pro…...

LOOI机器人的技术实现解析:从手势识别到边缘检测
LOOI机器人作为一款创新的AI硬件产品,通过将智能手机转变为具有情感交互能力的桌面机器人,展示了前沿AI技术与传统硬件设计的完美结合。作为AI与玩具领域的专家,我将全面解析LOOI的技术实现架构,特别是其手势识别、物体识别和环境…...
