TS的函数如何定义类型
如何接受arguments参数
function add(...args: string[]) {let list4: IArguments = arguments;}add('1', '2')自定义一个args
interface A1 {callee: Function,length: number,[index: number]: any}function adds(...args: string[]) {let list4: A1 = arguments;}adds('1', '2')多个参数
function add1(a: number, b: number): number {return a + b;}const add2 = (a: number, b: number): number => {return a + b;}默认值
const add3 = (a: number = 10, b: number = 15): number => {return a + b;}可选参数
const add4 = (a?: number, b?: number): void => {}定义一个对象参数
interface User {name: string,age: number}function getName(data: User): User {return data;}定义this参数
//ts 可以定义this 必须是第一个参数
interface Obj {list: number[],add: (this: Obj, num: number) => void}let obj: Obj = {list: [1, 2, 3, 4],add(this: Obj, num: number) {this.list.push(num);console.log(this.list)}}相关文章:

TS的函数如何定义类型
如何接受arguments参数 function add(...args: string[]) {let list4: IArguments arguments;}add(1, 2) 自定义一个args interface A1 {callee: Function,length: number,[index: number]: any}function adds(...args: string[]) {let list4: A1 arguments;}adds(1, 2) …...
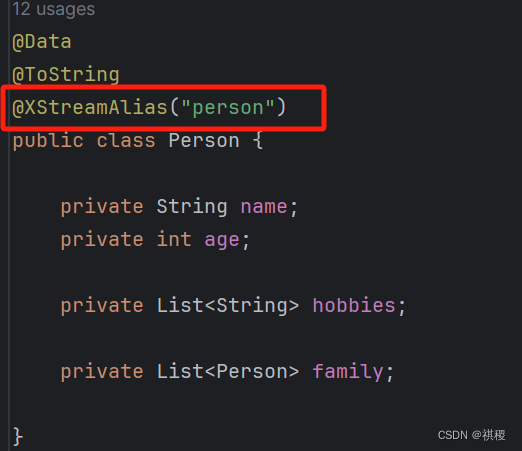
xstream实现xml和java bean 互相转换
目录 pom引用java bean 类XML 转换工具类测试类执行结果注意问题 JAXB方式见: JAXB实现XML和Bean相互转换 Java中实现XML和Bean的转换的方式或插件有以下几种: JAXB(Java Architecture for XML Binding):JAXB是Java …...

斯坦福机器学习 Lecture1 (机器学习,监督学习、回归问题、分类问题定义)
https://www.bilibili.com/video/BV1JE411w7Ub?p1&vd_source7a1a0bc74158c6993c7355c5490fc600 笔记如下 机器学习的定义:不需要明确编程就能让计算机去学习做某件事情 另一个定义 什么是监督学习? 给定一组 (x,y) 样本,学习一个 x-&g…...

五、Linux目录结构
1.基本介绍 1.Linux的文件系统是采用级层式的树状目录结构,在此结构中的最上层是根目录"r/",然后在此目录下再创建其他的目录。 2.深刻理解linux树状文件目录是非常重要的 3.记住一句经典的话:在Linux世界里,一切皆文件…...

C/C++数据结构之中缀表达式转换为后缀表达式,删除堆栈元素
在这篇博客中,我们将深入分析一个使用C编写的栈和表达式计算程序。该程序不仅实现了基本的栈操作,还提供了中缀表达式转后缀表达式和删除堆栈中的元素等实用功能。通过逐一讲解每个函数的功能,我们将更全面地理解这个程序的实现。 资源获取&a…...

uni-app下,页面跳转后wacth持续监听的问题处理
uni-app下,页面跳转后wacth持续监听的问题处理 好久没写博客了,最近碰到了一个uni-app(vue2)开发小程序的问题,个人觉得很典型,所以拿出来给各位做个参考。 需求场景: 全局轮询用户权限。简单…...

Python技术栈 —— 语言基础
Python基础 语法拾遗List与Tuple的区别yield关键字for in enumeratefor in zip 精彩片段测量程序用时 语法拾遗 List与Tuple的区别 ListTuple建立后是否可变可变不可变建立后是否可添加元素可添加不可添加 # list and tuple List [1, 2, 3, 4, 5] Tuple (1, 2, 3, 4, 5) p…...

redis cluster搭建
k8s部署 Redis Insight k8s部署redis集群_mob6454cc6c6291的技术博客_51CTO博客 占用的内存竟然这么小,才200M左右 随便选个节点进去,看能否连接上其他节点 redis-cli -h redis-cluster-v1-0.redis-cluster.project-gulimall.svc.cluster.local 再创建个…...

windows 11 本地运行ER-NeRF及pytorch3D安装
ER-NeRF本地运行只要梳理好依赖版本,运行起来就很顺畅 conda create -n ernerf python3.10 创建本项目虚拟环境conda install pytorch1.12.1 torchvision0.13.1 cudatoolkit11.3 -c pytorch 若windows有多个版本的cuda,需要在环境变量中切换至cuda 11.3&…...

mysql客户端navicat的一些错误合集
关于mysql的客户端的使用的一些问题 问题描述: 在使用navicat prenium客户端的时候,连接数据库出现 Table ‘performance_schema.session_variables’ doesn’t exist 错误 解决方案: 首先找到mysql的bin目录 然后winR 进入到cmd界面 输入…...
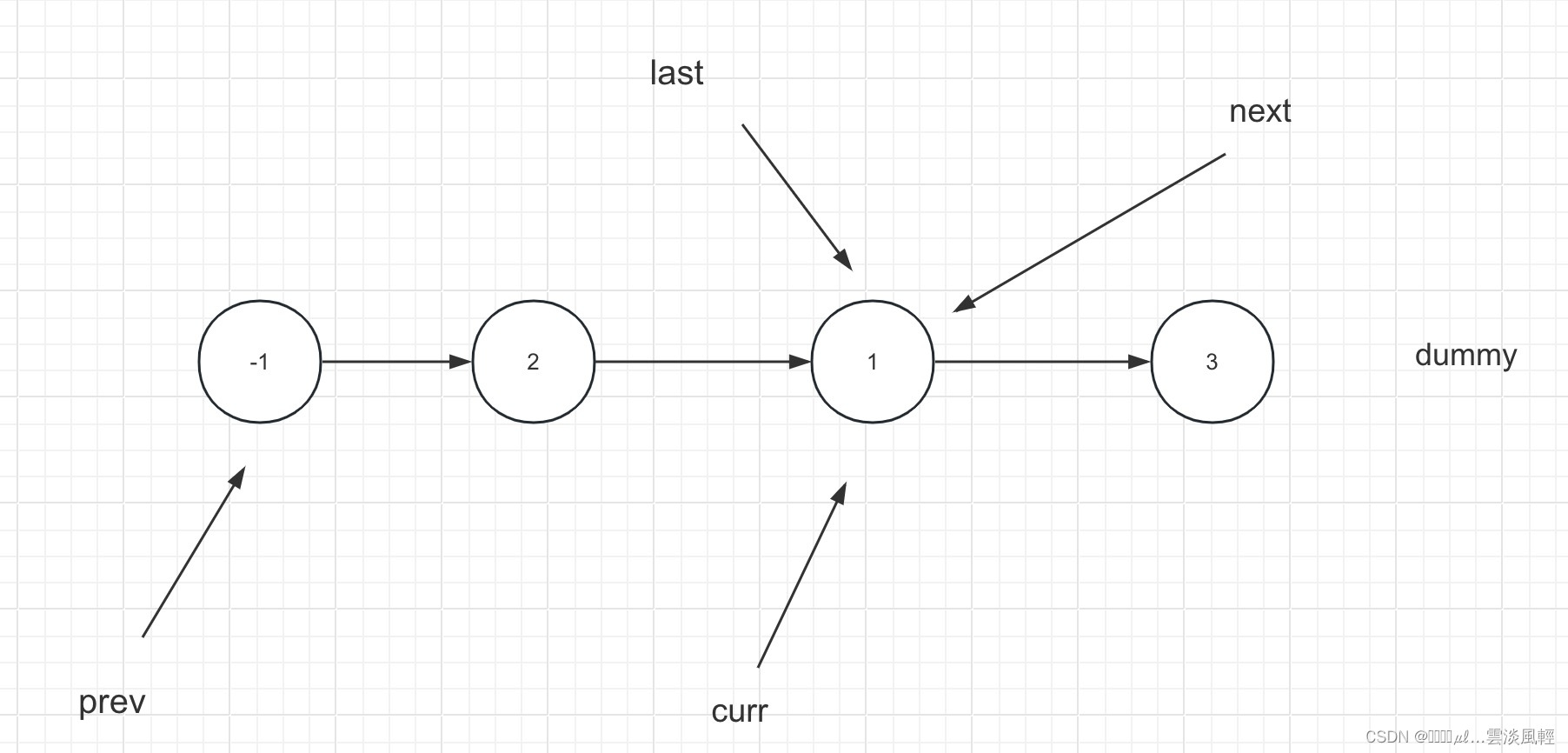
【力扣面试经典150题】(链表)K 个一组翻转链表
题目描述 力扣原文链接 给你链表的头节点 head ,每 k 个节点一组进行翻转,请你返回修改后的链表。 k 是一个正整数,它的值小于或等于链表的长度。如果节点总数不是 k 的整数倍,那么请将最后剩余的节点保持原有顺序。 你不能只…...
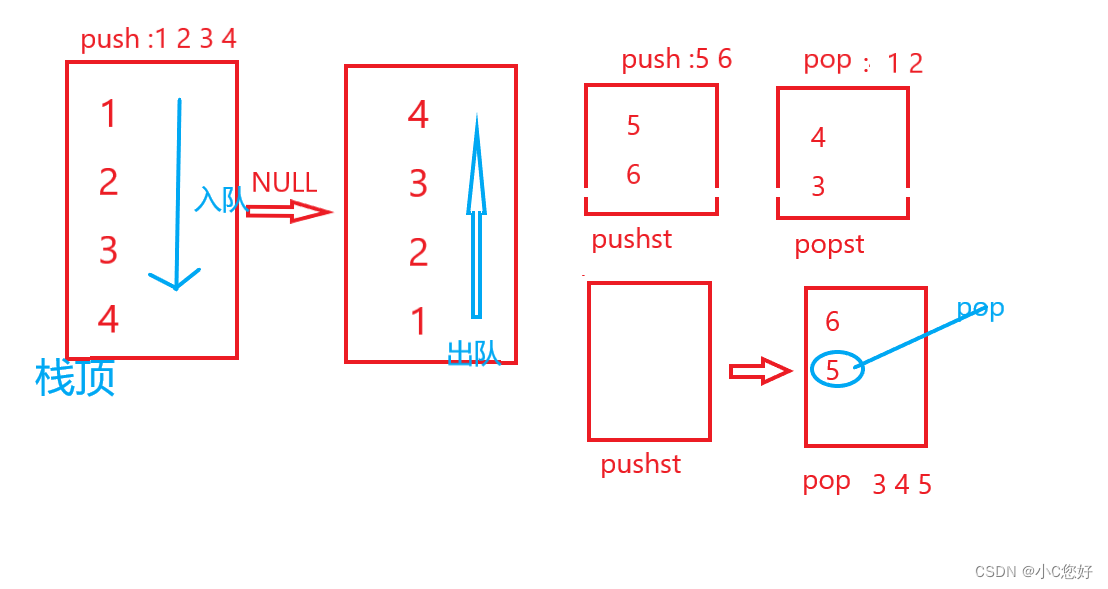
数据结构刷题
空间复杂度:临时开辟的空间、空间是可以重复利用的 递归为O(n) 时间复杂度:程序执行次数 消失的数字 力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台 思路1:利用连续的特点求等差和然后减去所有元素得到的就是消…...

【Android】设置全局标题栏
序言 在做项目的时候,有时候需要一个全局统一的标题栏,保证项目风格的统一,但是如果在每个activity上面都写一遍这个标题栏就很麻烦了,我们经常用的方法就是写个基类Activity,然后当某个Activity需要这个统一的标题栏…...

R语言的入门学习
目录 准备工作导入csv数据集选择前200行作为数据集展示数据集的前/后几N行宏观分析删除缺失值构建直方图导出为图片 R语言常见图像类型例1:散点图例2:散点矩阵图 准备工作 安装教程: R语言和RStudio的下载安装(非常简便舒适&…...

【开源】基于Vue和SpringBoot的民宿预定管理系统
项目编号: S 058 ,文末获取源码。 \color{red}{项目编号:S058,文末获取源码。} 项目编号:S058,文末获取源码。 目录 一、摘要1.1 项目介绍1.2 项目录屏 二、功能模块2.1 用例设计2.2 功能设计2.2.1 租客角色…...

nacos集群部署
GitHub - nacos-group/nacos-k8s: This project contains a Nacos Docker image meant to facilitate the deployment of Nacos on Kubernetes using StatefulSets. 需要修改两个文件 --- apiVersion: v1 kind: Service metadata:name: nacos-headlessnamespace: project-guli…...

9、传统计算机视觉 —— 边缘检测
本节介绍一种利用传统计算机视觉方法来实现图片边缘检测的方法。 什么是边缘检测? 边缘检测是通过一些算法来识别图像中物体之间,或者物体与背景之间的边界,也就是边缘。 边缘通常是图像中灰度变化显著的地方,标志着不同区域的分界线。 在一张图像中,边缘可以是物体的…...
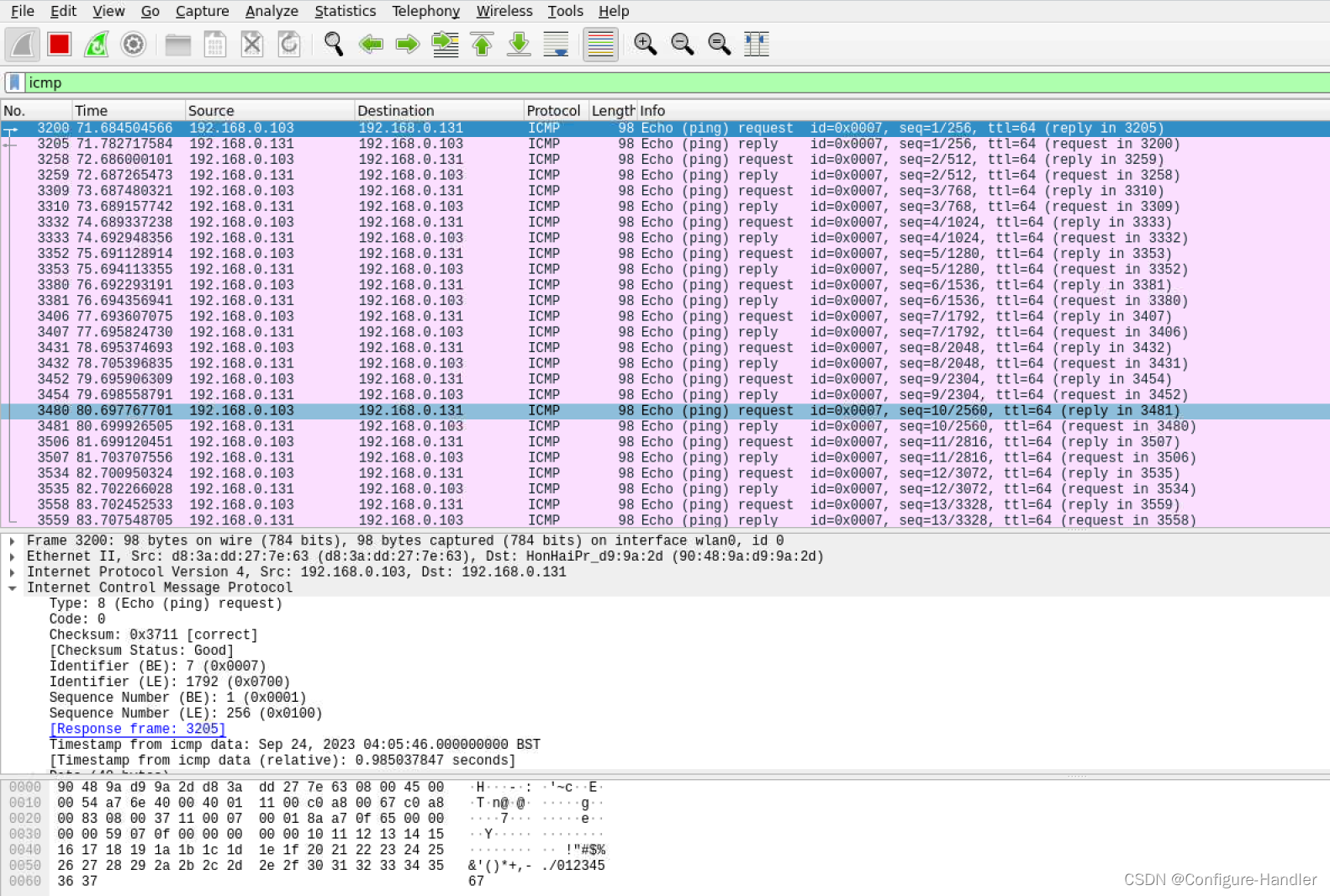
Linux tc 使用
tc模拟延时丢包等网络故障依赖的内核驱动 /lib/modules/5.15.0-52-generic/kernel/net/sched/sch_netem.ko有些系统并不是默认就安装上该驱动的,如果没有安装该驱动,构造网络故障时会报错。 root:curtis# tc qdisc change dev enp4s0 root netem delay…...

从0开始学习JavaScript--JavaScript 数字与日期
JavaScript中的数字和日期是处理数值计算和时间相关任务的核心。本文将深入研究JavaScript中数字的表示、常见运算,以及日期对象的创建、格式化等操作,并通过丰富的示例代码,可以更全面地了解和应用这些概念。 JavaScript数字基础 JavaScri…...

从关键新闻和最新技术看AI行业发展(2023.11.6-11.19第十期) |【WeThinkIn老实人报】
Rocky Ding 公众号:WeThinkIn 写在前面 【WeThinkIn老实人报】旨在整理&挖掘AI行业的关键新闻和最新技术,同时Rocky会对这些关键信息进行解读,力求让读者们能从容跟随AI科技潮流。也欢迎大家提出宝贵的优化建议,一起交流学习&…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...

android RelativeLayout布局
<?xml version"1.0" encoding"utf-8"?> <RelativeLayout xmlns:android"http://schemas.android.com/apk/res/android"android:layout_width"match_parent"android:layout_height"match_parent"android:gravity&…...

数据结构:递归的种类(Types of Recursion)
目录 尾递归(Tail Recursion) 什么是 Loop(循环)? 复杂度分析 头递归(Head Recursion) 树形递归(Tree Recursion) 线性递归(Linear Recursion)…...

Python训练营-Day26-函数专题1:函数定义与参数
题目1:计算圆的面积 任务: 编写一个名为 calculate_circle_area 的函数,该函数接收圆的半径 radius 作为参数,并返回圆的面积。圆的面积 π * radius (可以使用 math.pi 作为 π 的值)要求:函数接收一个位置参数 radi…...
