二叉搜索树实现
树的导览
树由节点(nodes)和边(edges)构成,如下图所示。整棵树有一个最上端节点,称为根节点(root)。每个节点可以拥有具有方向的边(directed edges),用来和其他节点相连。相连的节点之中,在上者称为父节点(parent),在下者称为子节点(child)。
一些基本概念:
- 节点的度:一个节点含有的子树的个数,如果最多只允许两个子节点,即为二叉树
- 叶节点:无子节点,即度为 0 的节点称为叶节点
- 兄弟节点:不同的节点拥有相同的父节点
- 路径长度:根节点到任何节点之间有唯一路径,路径所经过的边数
- 节点的深度:根节点到任一节点的路径长度,根节点的深度永远为 0
- 节点的高度:某节点到其叶节点的路径长度
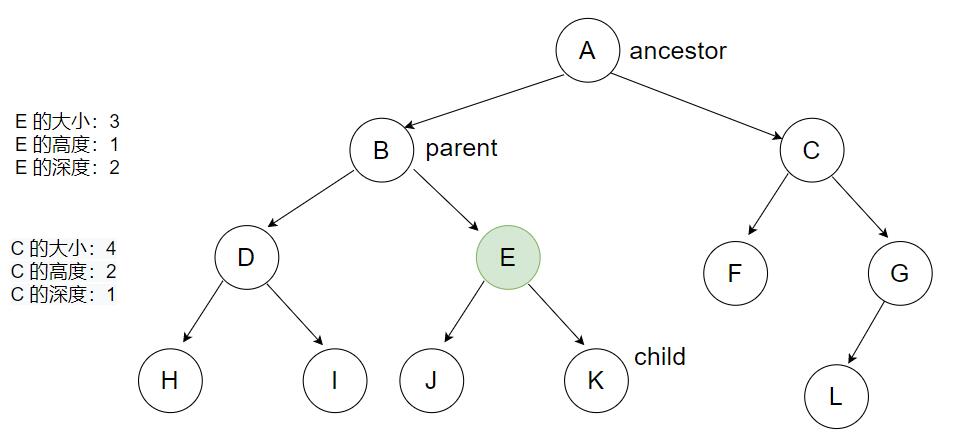
二叉搜索树的概念
二叉搜索树可以提供对数时间的元素插入和访问,是一种特殊的二叉树,具有以下规则:
- 任何节点的键值一定大于其左子树中的每一个节点的键值
- 任何节点的键值一定小于其右子树中的每一个节点的键值
因此二叉搜索树的最左节点是最小元素,最右节点是最大元素。
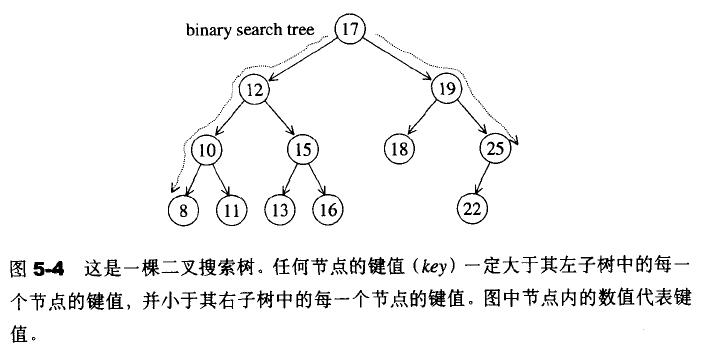
二叉搜索树的实现
节点的定义
该节点设计很简单:
- 包含三个成员变量:节点值、左孩子指针、右孩子指针
- 构造函数:将成员变量初始化
/// @brief 二叉树的节点
/// @tparam K 节点值的类型
template<class K>
struct BSTreeNode {BSTreeNode(const K& key = K()) : _key(key), _left(nullptr), _right(nullptr){}K _key; // 节点值BSTreeNode<K>* _left; // 左指针BSTreeNode<K>* _right; // 右指针
};
接口总览
文章完整代码:BinarySearchTree · 秦国维/data-structure
template<class K>
class BSTree {typedef BSTreeNode<K> Node;
public:Node* Find(const K& key);Node* _FindR(Node* _root, const K& key);Node* FindR(const K& key);bool Insert(const K& key);bool _InsertR(Node*& _root, const K& key);bool InsertR(const K& key);bool Erase(const K& key);bool _EraseR(Node*& root, const K& key);bool EraseR(const K& key);
private:Node* _root = nullptr;
};
查找
根据二叉搜索树的特性,可以在二叉搜索树快速的找到指定值:
- 若 key 值大于当前节点的值,在当前节点的右子树中查找
- 若 key 值小于当前节点的值,在当前节点的左子树中查找
- 若 key 值等于当前节点的值,返回当前节点的地址
- 若找到空,查找失败,返回空指针
非递归
/// @brief 查找指定 key 值
/// @param key 要查找的 key
/// @return 找到返回节点的指针,没找到返回空指针
Node* Find(const K& key) {Node* cur = _root;while (cur != nullptr) {// key 值与当前节点值比较if (key > cur->_key) {cur = cur->_right;} else if (key < cur->_key) {cur = cur->_left;} else {return cur;}}return nullptr;
}
递归
Node* _FindR(Node* root, const K& key) {if (root == nullptr) {return nullptr;}// key 值与当前节点值比较if (key > root->_key) {// key 值大于当前节点的值,递归到右子树查找return _FindR(root->_right, key);} else if (key < root->_key) {// key 值小于当前节点的值,递归到左子树查找return _FindR(root->_left, key);} else {return root;}
}Node* FindR(const K& key) {return _FindR(_root, key);
}
插入
根据二叉搜索树的性质,插入操作也很简单:
- 如果是空树,将插入的节点作为根节点
- 如果不是空树,利用性质找到该插入的位置,将节点插入
插入新元素时,从根节点开始,遇到键值较大的就向左,遇到键值较小的就向右,一直到尾端,即为插入点。
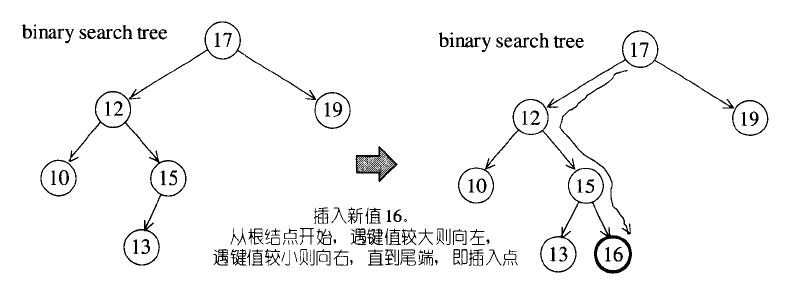
非递归
使用非递归插入函数时,需要定义一个 parent 指针,该指针用来指示插入节点的父节点,以便将新节点插入。
/// @brief 在二叉搜索树中插入指定节点
/// @param key 节点的 key 值
/// @return 成功返回 true,失败返回 false
bool Insert(const K& key) {if (_root == nullptr) {// 第一个插入的节点,构建为根_root = new Node(key);return true;}// 先找到要插入的位置Node* parent = nullptr;Node* cur = _root;while (cur != nullptr) {if (key > cur->_key) {parent = cur;cur = cur->_right;} else if (key < cur->_key) {parent = cur;cur = cur->_left;} else {// 已经有该值了,插入失败return false;}}// 创建要插入的节点cur = new Node(key);// 看插入节点在父节点哪边if (key > parent->_key) {parent->_right = cur;} else {parent->_left = cur;}return true;
}
递归
递归版本的插入相对于非递归版本更简单,要注意的是 Node* 参数一定要传引用,这样才能改变父亲指针的指向。
bool _InsertR(Node*& _root, const K& key) {if (_root == nullptr) {// 因为传递的是引用,所以可以直接改变指向_root = new Node(key);return true;}// 判断 key 与当前节点值大小关系if (key > _root->_key) {// key 更大就递归到右子树插入return _InsertR(_root->_right, key);} else if (key < _root->_key) {// key 更小就递归到左子树插入return _InsertR(_root->_left, key);} else {return false;}return false; // 为了消除编译警告
}bool InsertR(const K& key) {return _InsertR(_root, key);
}
删除
删除相对与插入就复杂的多了,需要考虑三种情况:
- 待删除节点没有子树
- 待删除节点有一个子树
- 待删除节点有两个子树
下面就来讨论这三种情况:
待删除节点没有子树
这种情况比较简单,直接将指向该节点的指针置空即可。
待删除节点有一个子树
如果节点 Q 只有一个子节点,就直接将 Q 的子节点连至 Q 的父节点,并将 Q 删除。

待删除节点有两个子树
这时就比较复杂了,需要使用替换法。如果 Q 有两个节点,就以右子树的最小节点取代 Q(左子树的最大节点也可以)。
右子树最小节点获取方法:从右子节点开始,一直向左找到底。
为什么右子树最小节点可以替换当前节点?
因为右子树最小节点一定大于当前节点左子树中的所有节点,又一定小于右子树中的其他节点,故不会破坏二叉搜索树的规则。
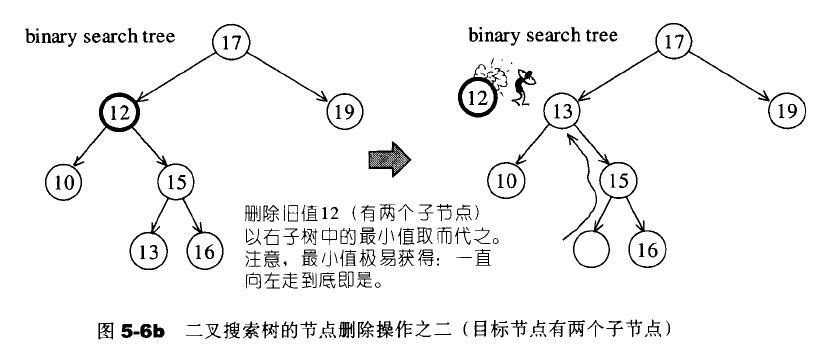
非递归
该实现版本同样需要定义一个 parent 指针,以便将其孩子托付给父亲。
/// @brief 在二叉搜索树中删除指针节点
/// @param key 删除节点的 key
/// @return 删除成功返回 true,失败返回 false
bool Erase(const K& key) {Node* parent = nullptr;Node* cur = _root;// 先找要删除节点的位置while (cur != nullptr) {if (key > cur->_key) {// 大于就到右子树中找parent = cur;cur = cur->_right;} else if (key < cur->_key) {// 小于就到左子树中找parent = cur;cur = cur->_left;} else {// 找到要删除的节点了if (cur->_left == nullptr) {// cur 左孩子为空,即只有一个右孩子或没有孩子if (parent == nullptr) {// 如果要删除的是根节点,更换新根_root = _root->_right;} else {if (parent->_left == cur) {parent->_left = cur->_right;} else {parent->_right = cur->_right;}}// 释放掉 cur 指向的空间delete cur;cur = nullptr;} else if (cur->_right == nullptr) {// 此时说明只有左孩子if (parent == nullptr) {// 如果要删除的是根节点,更换新根_root = _root->_left;} else {if (parent->_left == cur) {parent->_left = cur->_left;} else {parent->_right = cur->_left;}}// 释放掉 cur 指向的空间delete cur;cur = nullptr;} else {// 此时有左右孩子,需要使用替换法删除Node* minParent = cur;Node* min = cur->_right;// 先找到右子树的最左节点while (min->_left != nullptr) {minParent = min;min = min->_left;}// 将最小节点的值替换到 cur 上cur->_key = min->_key;if (minParent->_left == min) {// 最小节点位于父节点的左边,将它的右子树托付给父节点minParent->_left = min->_right;} else {// 最小节点位于父节点的右边,这时就是 cur 的右子树没有左子树// minNode->_left 一定为空,写成这样比较对称minParent->_right = min->_left;}delete min;min = nullptr;} // end of if (cur->_left == nullptr)return true;} // end of if (key > cur->_key)} // end of while (cur != nullptr)// 没找到要删除的节点,返回 falsereturn false;
}
递归
递归版本的删除相对于非递归版本更简单,要注意的是 Node* 参数一定要传引用,这样才能改变父亲指针的指向,将节点删除。
bool _EraseR(Node*& root, const K& key) {if (root == nullptr) {// 没找到要删除的节点返回 falsereturn false;}if (key > root->_key) {// key 更大就到右子树中删除_EraseR(root->_right, key);} else if (key < root->_key) {// key 更小就到左子树中删除_EraseR(root->_left, key);} else {Node* del = root;if (root->_left == nullptr) {// 此时左为空或左右为空,只需要将右子树给父节点即可// 左右为空时,右子树为空,不会违反规则root = root->_right;} else if (root->_right == nullptr) {// 此时右为空,只需要将左子树给父节点root = root->_left;} else {// 有两个孩子,需要替换法删除Node* min = root->_right;while (min->_left != nullptr) {min = min->_left;}// 把最小的节点的值换上root->_key = min->_key;// 递归到右子树,将 minnode 删掉// 一定要 return,否则会重复释放return _EraseR(root->_right, min->_key);}delete del;del = nullptr;return true;}return false; // 为了消除编译警告
}bool EraseR(const K& key) {return _EraseR(_root, key);
}
相关文章:

二叉搜索树实现
树的导览 树由节点(nodes)和边(edges)构成,如下图所示。整棵树有一个最上端节点,称为根节点(root)。每个节点可以拥有具有方向的边(directed edges)…...
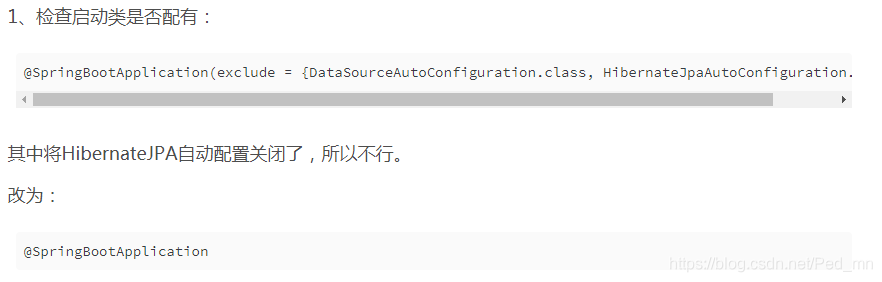
解决Spring Data Jpa 实体类自动创建数据库表失败问题
先说一下我遇到的这个问题,首先我是通过maven创建了一个spring boot的工程,引入了Spring data jpa,结果实体类创建好之后,运行工程却没有在数据库中自动创建数据表。 找了半天发现是一个配置的问题! hibernate.ddl-auto节点的配…...

Elasticsearch:创建一个简单的 “你的意思是?” 推荐搜索
“你的意思是” 是搜索引擎中一个非常重要的功能,因为它们通过显示建议的术语来帮助用户,以便他可以进行更准确的搜索。比如,在百度中,我们进行搜索时,它通常会显示一些更为常用推荐的搜索选项来供我们选择:…...
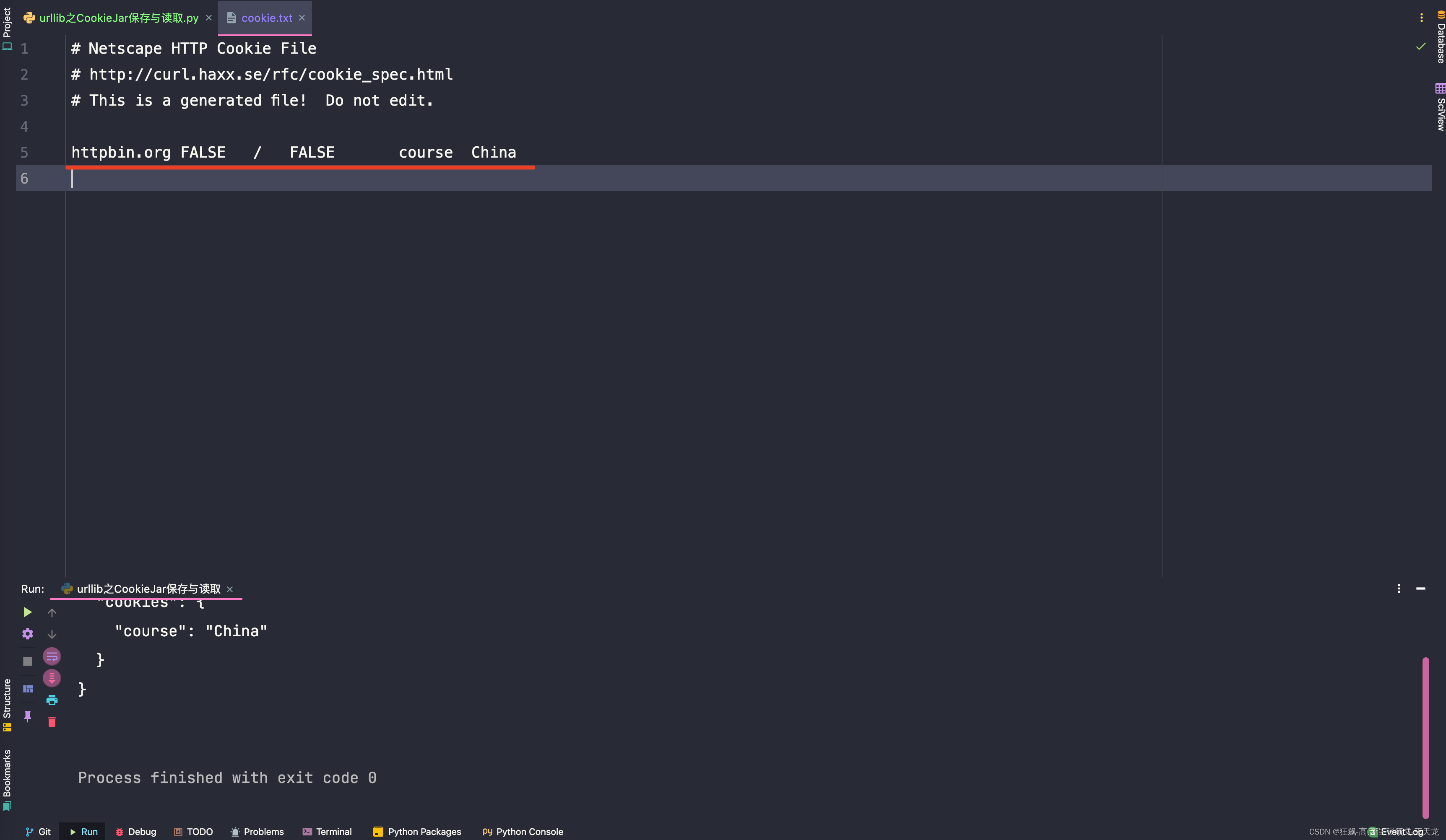
urllib之ProxyHandler代理以及CookieJar的cookie内存传递和本地保存与读取的使用详解
处理更高级操作时(Cookies处理,代理设置),需要一个强大的工具Handler,可以理解成各种处理器,有处理登录认证的、有处理Cookies的、有处理代理设置的。利用这些几乎可以做到HTTP请求中所有事情。当中urllib.request模块里的 BaseHa…...

华为造车锚定智选模式, 起点赢家赛力斯驶入新能源主航道
文|螳螂观察 作者| 易不二 近日,赛力斯与华为的一纸联合业务深化合作协议,给了频频猜测赛力斯与华为之间关系的舆论一个明确的定调:智选模式已成为华为与赛力斯共同推动中国新能源汽车产业高质量发展的坚定选择。 自华为智能汽车业务开启零…...
[oeasy]python0096_游戏娱乐行业_雅达利_米洛华_四人赛马_影视结合游戏
游戏娱乐行业 回忆上次内容 游戏机行业从无到有 雅达利 公司 一枝独秀并且带领 行业 发展起来 雅达利公司 优秀员工 乔布斯 在 朋友 帮助下完成了《pong》 Jobs 黑了 Woz 一部分收入 然后拿着钱 去印度禅修了 游戏行业 会如何继续 呢??🤔 灵修 乔布…...

使用python测试框架完成自动化测试并生成报告-实例练习
练习一: 使用unittest 完成自动化测试并使用HttpTestRunner生成报告 1、写个简单的计算器功能,大小写转换功能,随机生成字符串功能 2、编写测试用例,不同的数据(你能想到的所有测试用例),并进行断言。除0的…...
JavaWeb 实战 01 - 计算机是如何工作的
计算机是如何工作的1. 计算机发展史2. 计算机的基本组成2.1 冯诺依曼体系结构2.2 CPU的内部结构2.3 指令2.3.1 指令表2.3.1.1 寄存器2.3.2 CPU的工作流程2.4 小结3. 操作系统3.1 核心功能3.2 操作系统的软硬件结构3.3 什么是进程 / 任务3.4 进程管理3.4.1 管理3.4.2 PCB : 进程…...
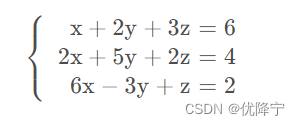
线性代数学习-1
线性代数学习-1行图像和列图像行图像列图像总结本文转载于https://herosunly.blog.csdn.net/article/details/88698381 该文章本人认为十分有用,便自己敲一遍笔记加固印象原文链接 原文这个笔记感觉比我老师讲的更加透彻,清晰。很好的展示了线性代数的原…...

人工智能写的十段代码,九个通过测试了
“抢走你工作的不会是 AI ,而是先掌握 AI 能力的人” 编程测试 1. 我想用golang实现二叉树前序,请你帮我写一下代码。 // 定义二叉树节点 type TreeNode struct {Val intLeft *TreeNodeRight *TreeNode }// 前序遍历 func PreOrderTraversal(root *Tre…...

巴塞尔问题数值逼近方法
巴塞尔问题:计算所有平方数的导数和 ∑n1∞1n2limn→∞(112122⋯1n2)\sum_{n1}^{\infty} \frac{1}{n^{2}}\lim _{n \rightarrow\infty}\left(\frac{1}{1^{2}}\frac{1}{2^{2}}\cdots\frac{1}{n^{2}}\right)n1∑∞n21n→∞lim(121221⋯n21) 其理论解为…...

【深度学习环境】Docker
1. Docker 相关安装配置 1.1 docker 安装 参考:https://www.runoob.com/docker/ubuntu-docker-install.html 1.2 nvidia-docker 安装 参考:https://zhuanlan.zhihu.com/p/37519492 1.3 代理加速 参考:https://yeasy.gitbook.io/docker_…...
基于vscode开发vue项目的详细步骤教程 2 第三方图标库FontAwesome
1、Vue下载安装步骤的详细教程(亲测有效) 1_水w的博客-CSDN博客 2、Vue下载安装步骤的详细教程(亲测有效) 2 安装与创建默认项目_水w的博客-CSDN博客 3、基于vscode开发vue项目的详细步骤教程_水w的博客-CSDN博客 目录 六、第三方图标库FontAwesome 1 安装FontAwesome 解决报…...

今天面了个腾讯拿25K出来的软件测试工程师,让我见识到了真正的天花板...
今天上班开早会就是新人见面仪式,听说来了个很厉害的大佬,年纪还不大,是上家公司离职过来的,薪资已经达到中高等水平,很多人都好奇不已,能拿到这个薪资应该人不简单,果然,自我介绍的…...

OSG三维渲染引擎编程学习之六十九:“第六章:OSG场景工作机制” 之 “6.9 OSG数据变量”
目录 第六章 OSG场景工作机制 6.9 OSG数据变量 第六章 OSG场景工作机制 作为一个成熟的三维渲染引擎,需要提供快速获取场景数据、节点等信息,具备自定义数据或动画更新接口,能接收应用程序或窗口等各类消息。OSG三维渲染引擎能较好地完成上述工作,OSG是采用什么方式或工作…...

Tektronix泰克TDP3500差分探头3.5GHz
附加功能: 带宽:3.5 GHz 差分输入电容:≤0.3 pF 差分输入电阻:100 kΩ DC pk 交流输入电压:15 V >60 dB 在 1 MHz 和 >25 dB 在 1 GHz CMRR 出色的共模抑制——减少较高共模环境中的测量误差 低电容和电阻负载…...
轻松实现内网穿透:实现远程访问你的私人网络
导语:内网穿透是什么?为什么我们需要它?今天我们将介绍这个令人惊叹的技术,让你实现远程访问你的私人网络。 使用内网穿透,轻松实现外网访问本地部署的网站 第一部分:什么是内网穿透? 通俗解释…...

MySQL长字符截断
MySQL超长字符截断又名"SQL-Column-Truncation",是安全研究者Stefan Esser在2008 年8月提出的。 在MySQL中的一个设置里有一个sql_mode选项,当sql_mode设置为default时,即没有开启STRICT_ALL_TABLES选项时(MySQLsql_mo…...

python计算量比指标
百度百科是这么写的:量比定义:股市开市后平均每分钟的成交量与过去5个交易日平均每分钟成交量之比。计算公式:量比(现成交总手数 / 现累计开市时间(分) )/ 过去5日平均每分钟成交量。这里公式没有问题,但是…...
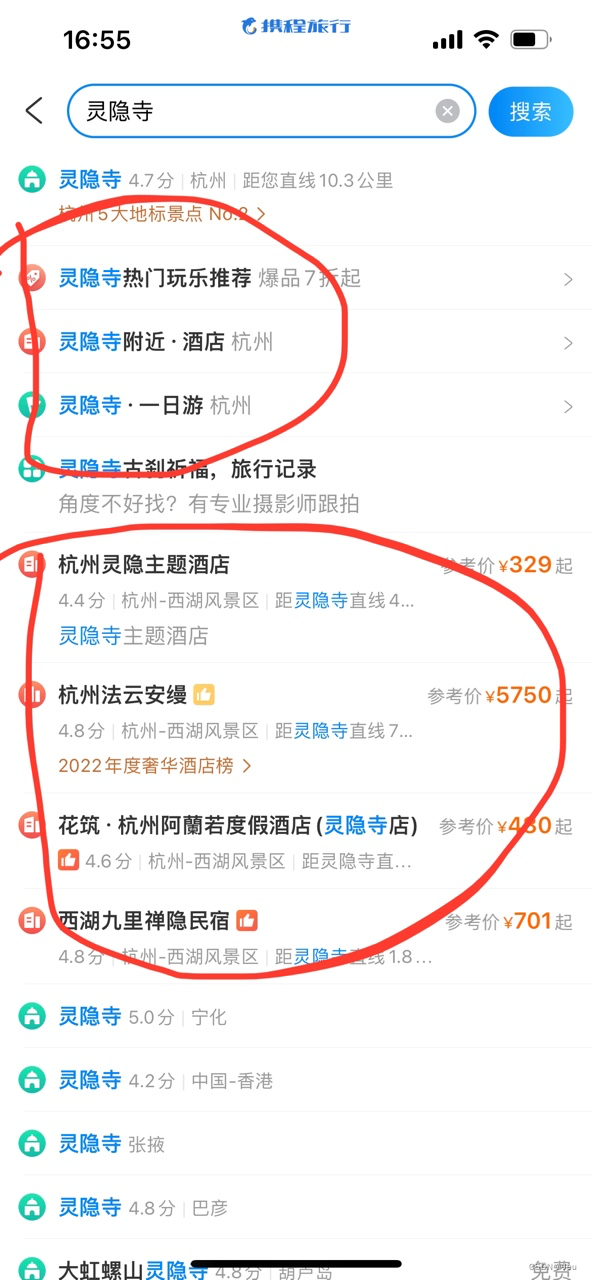
下拉框推荐-Suggest-SUG
什么是下拉框推荐 在我们使用各种app(飞猪)想要搜索我们想要的东西,假设我想要上海迪士尼的门票,那么精确的query是“上海迪士尼门票”,要打7个字,如果在你输入“上海”的时候app就推荐了query“上海迪士尼…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...
