React整理总结(三)
1.props和state的更新
- 父组件重新render时,所有的子组件也会调用render()函数。shouldComponentUpdate(nextProp, nextState)
shouldComponentUpdate(nextProps, nextState) {if (equal(nextProps, this.props) && equal(nextState, this.state)){return false} else {return true;}
}
- PureComponent。只是对props和state进行了浅层比较
- React.memo(),针对函数组件
2.ref获取原生DOM
- 字符串
this.refs.domRef | <div ref="domRef" /> - 创建ref
this.titleRef = React.createRef() | <div ref={this.titleRef} /> - 函数返回
<div ref={el => this.elRef = el} /> - ref可以直接获取类组件实例,
<MyComponent ref={this.comRef} /> - ref获取函数式组件,需要使用forwardRef.
const MyComponent = React.forwardRef(function (props, ref){
return <div ref={ref} />
})
3.高阶组价
- 高阶函数:接受函数作为参数或者返回值为函数
- 高阶组件(HOC):接受组件作为参数,并且返回新组件
增强props
配合context使用,传递state
登录鉴权
生命周期劫持
…
4. Portals与Fragment
createPortal(content, target)将content内容挂载到target上
// html的body, 正常内容都是挂在root下
<div id="root"></div>
<div id="modal"></div>// Modal组件
import React, {PureComponent } from “react”;
import { createPortal } from 'react-dom';
export default class Modal extends PureComponent {constructor(props){super(props);}render(){return createPortal(this.props.children, document.querySelector("#modal")); }
}
- Fragment, 短语法
<></>, 添加key时无法使用短语法
5. 严格模式StrictMode
- 识别不安全的生命周期
- 使用过时的ref APi
- 检查意外的副作用,constructor会被调用两次,生产模式不会
- 检查废弃的findDOMNode函数
- 检查过时的context api
相关文章:
)
React整理总结(三)
1.props和state的更新 父组件重新render时,所有的子组件也会调用render()函数。shouldComponentUpdate(nextProp, nextState) shouldComponentUpdate(nextProps, nextState) {if (equal(nextProps, this.props) && equa…...

天气这么好,都外出了。顺便了解一下漏桶算法
看到标题,你想到了些什么呢? 又是一个阳光明媚的周末,大家都外出了,路上到处堵车,尤其是各桥梁、隧道入口处,很多车排队等着进入,而出口处就像一个漏桶一样,一辆车接着一辆车有序且…...

【FPGA】Verilog:实现 RS 触发器 | Flip-Flop | 使用 NOR 的 RS 触发器 | 使用 NAND 的 RS 触发器
目录 0x00 RS 触发器(RS Flip-Flop) 0x01 实现 RS 触发器 0x02 使用 NOR 的 RS 触发器 0x03 使用 NAND 的 RS 触发器 0x00 RS 触发器(RS Flip-Flop) 触发器(Flip-Flop)是一种带有时钟的二进制存储设备…...
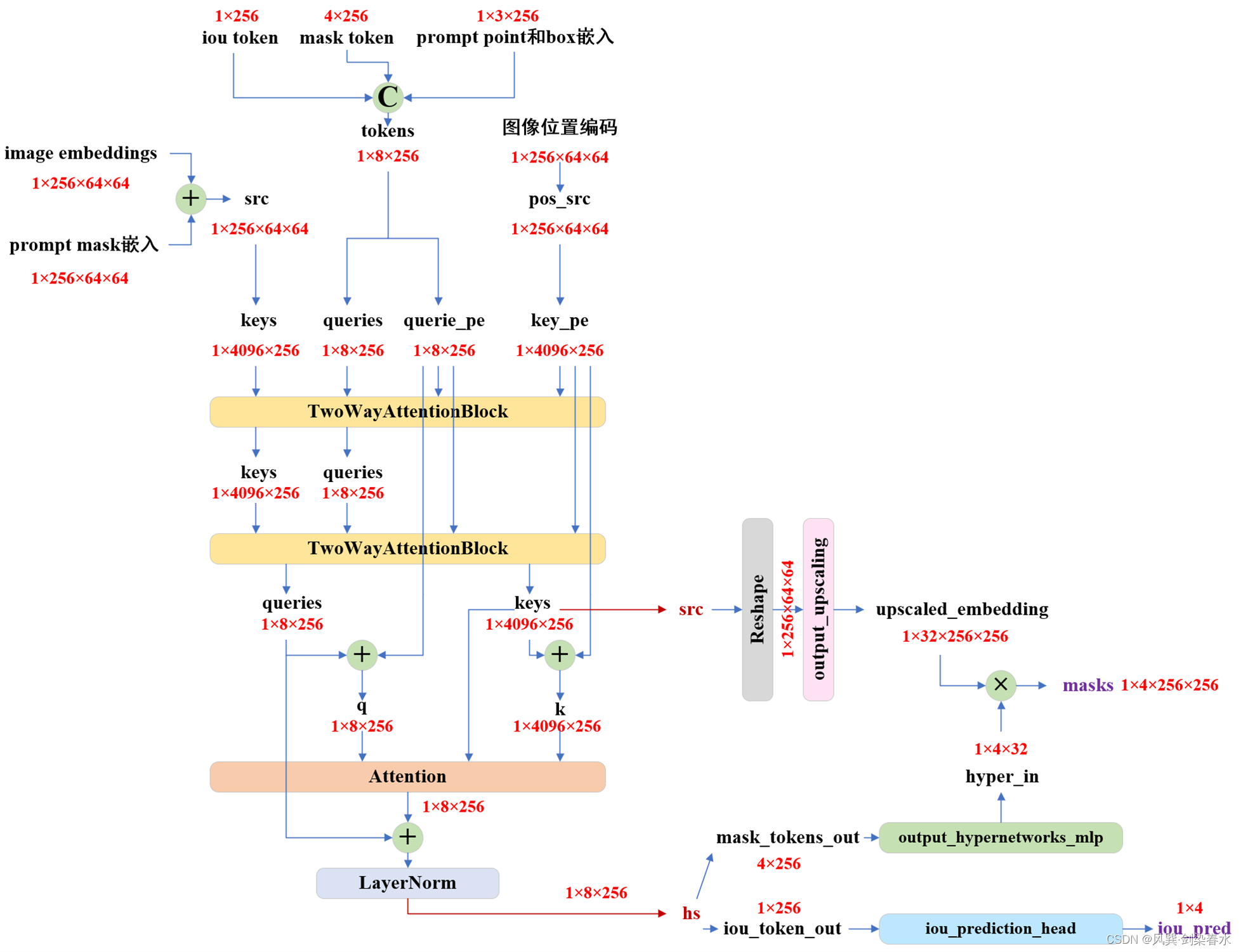
【技术追踪】SAM(Segment Anything Model)代码解析与结构绘制之Mask Decoder
论文:Segment Anything 代码:https://github.com/facebookresearch/segment-anything 系列篇: (1)【技术追踪】SAM(Segment Anything Model)代码解析与结构绘制之Image Encoder &am…...
认识Tomcat
文章目录 什么是tomcat?tomcat的使用tomcat的下载tomcat的目录结构tomcat的启动在tomcat上部署页面通过浏览器访问部署的页面 学习servlet的原因 什么是tomcat? 盖棺定论:Tomcat是一个HTTP服务器。 我们接下来要长期学习的东西都是关于前后…...

c语言通信之串口通信
在C语言中,可以使用串口通信、网络通信等多种方式实现计算机之间的通信。其中,串口通信通常用于近距离、低速率的通信,而网络通信则适用于远距离、高速率的通信。 下面以串口通信为例,介绍在C语言中如何实现串口通信。 1.打开串…...
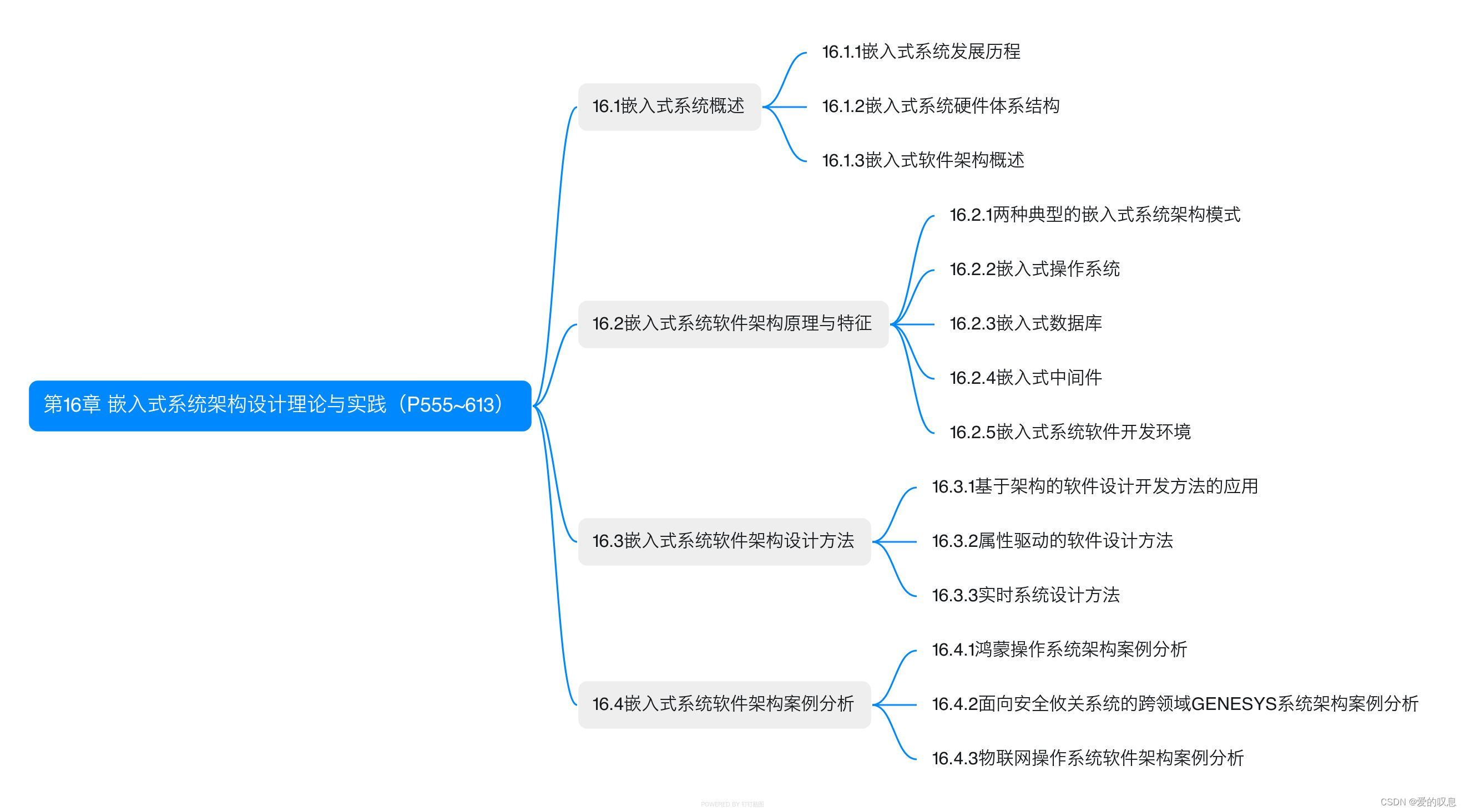
软考-高级-系统架构设计师教程(清华第2版)【第16章 嵌入式系统架构设计理论与实践(P555~613)-思维导图】
软考-高级-系统架构设计师教程(清华第2版)【第16章 嵌入式系统架构设计理论与实践(P555~613)-思维导图】 课本里章节里所有蓝色字体的思维导图...
2024年山东省职业院校技能大赛中职组 “网络安全”赛项竞赛试题-B卷
2024年山东省职业院校技能大赛中职组 “网络安全”赛项竞赛试题-B卷 2024年山东省职业院校技能大赛中职组 “网络安全”赛项竞赛试题-B卷A模块基础设施设置/安全加固(200分)A-1:登录安全加固(Windows, Linux)A-2&#…...

【Python数据结构与算法】——(线性结构)精选好题分享,不挂科必看系列
🌈个人主页: Aileen_0v0🔥系列专栏:<<Python数据结构与算法专栏>>💫个人格言:"没有罗马,那就自己创造罗马~" 时间复杂度大小比较 1.time complexity of algorithm A is O(n^3) while algorithm B is O(2^n). Which o…...
)
大数据-之LibrA数据库系统告警处理(ALM-12054 证书文件失效)
告警解释 系统在每天二十三点检查当前系统中的证书文件是否失效(即当前集群中的证书文件是否过期,或者尚未生效)。如果证书文件失效,产生该告警。 当重新导入一个正常证书,并且状态不为失效状态,该告警恢…...

Linux 之 journalctl 查看系统与 kernel 日志
目录 1. Linux 之 journalctl 查看系统与 kernel 日志 1. Linux 之 journalctl 查看系统与 kernel 日志 1 概述 日志管理工具 journalctl 是 centos7 上专有的日志管理工具, 该工具是从 message 这个文件里读取信息。Systemd 统一管理所有 Unit 的启动日志。带来的好处就是, …...

【PTA题目】7-3 冰雹猜想。 分数 10
7-3 冰雹猜想。 分数 10 全屏浏览题目 切换布局 作者 赵静静 单位 浙江工贸职业技术学院 冰雹猜想的内容是:任何一个大于1的整数n,按照n为偶数则除等2,n为奇数则乘3后再加1的规则不断变化,最终都可以变化为1。 例如ÿ…...

springBoot 配置druid多数据源 MySQL+SQLSERVER
1:pom 文件引入数据 <dependency> <groupId>com.alibaba</groupId> <artifactId>druid-spring-boot-starter</artifactId> <version>1.1.0</version> </dependency>…...
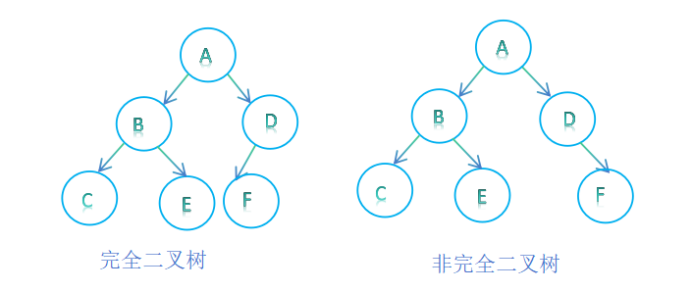
二叉树的创建与遍历
目录 前言: 二叉树的概念与结构 二叉树的链式存储 二叉树的创建 二叉树的销毁 二叉树结点个数计算 二叉树叶子结点个数计算 二叉树第k层节点个数的计算 二叉树高度的计算 二叉树查找值为x的结点 二叉树的遍历 二叉树的前序遍历 二叉树的中序遍历 二叉树…...

Mysql相关操作命令合集
参考文档:2021-06-25MySQL8.0创建用户和权限控制 - 简书 mysql登陆命令: mysql -u用户名 -p密码; 若遇到复杂密码,包含特殊字符,则需要做转义(以下密码为:rootry?elyl!): mysql…...
前端开发学习 (一) 搭建Vue基础环境
一、环境搭建 1、安装nodejs #下载地址 https://nodejs.org/dist/v20.9.0/node-v20.9.0-x64.msi 2、配置环境变量 上面下载完安装包后自行安装,安装完成后安装下图操作添加环境变量 #查看版本 node --version v20.9.0# npm --version 10.1.03、配置npm加速源 np…...

二维码智慧门牌管理系统升级解决方案:查询功能大提升,让地址查找变得轻松便捷!
文章目录 前言一、支持地址名称、小区等信息进行模糊查询二、支持地图上绘制多边形、圆形、矩形进行范围查询三、高效的数据处理能力,保证查询速度四、灵活的应用场景,满足多种需求 前言 随着科技的快速发展和城市化的加速推进,传统的门牌管…...
vite+vue3+electron开发环境搭建
环境 node 18.14.2 yarn 1.22 项目创建 yarn create vite test01安装vue环境 cd test01 yarn yarn dev说明vue环境搭建成功 安装electron # 因为有的版本会报错所以指定了版本 yarn add electron26.1.0 -D安装vite-plugin-electron yarn add -D vite-plugin-electron根目…...
:多态介绍与代码演示)
C#入门(9):多态介绍与代码演示
多态性是面向对象编程的一个核心概念,它允许你使用一个父类引用来指向一个子类对象。这可以使程序具有可扩展性,并且可以用来实现一些高级编程技术,如接口、事件、抽象类等。 多态相关的概念 以下是一些在C#中使用多态性的关键概念…...

可拖动、可靠边的 popupWindow 实现
0 背景 开发要实现一个可以拖动的圆角小窗,要求松手时,哪边近些靠哪边。并且还规定了拖动范围。样式如下: 1 实现 首先把 PopupWindow 的布局文件 pop.xml 实现 <?xml version"1.0" encoding"utf-8"?> <R…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...
