【Python数据结构与算法】——(线性结构)精选好题分享,不挂科必看系列

🌈个人主页: Aileen_0v0
🔥系列专栏:<<Python数据结构与算法专栏>>
💫个人格言:"没有罗马,那就自己创造罗马~"
时间复杂度大小比较
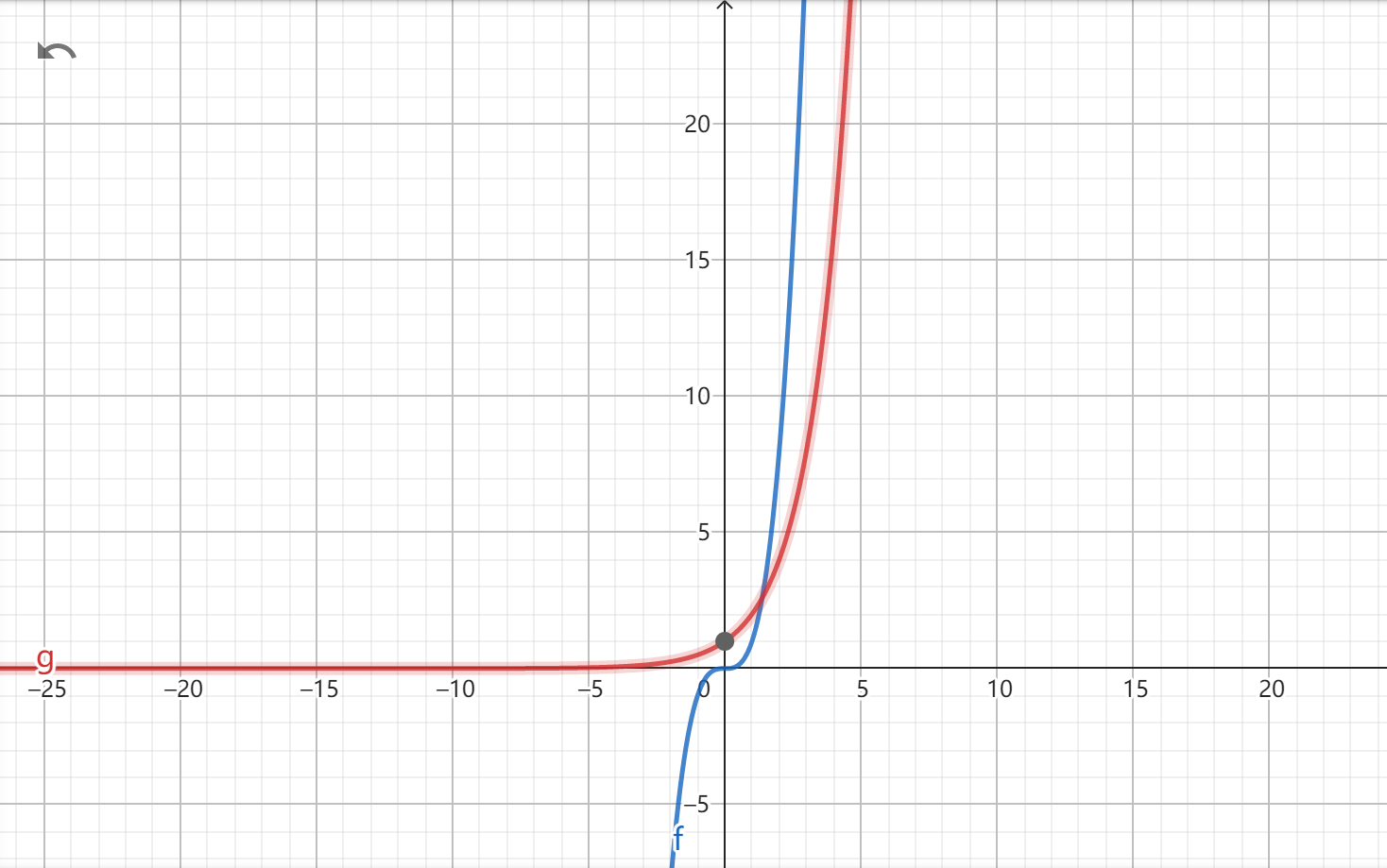
1.time complexity of algorithm A is O(n^3) while algorithm B is O(2^n). Which of the following statement is TRUE?
A.For any problem in any scale, the alogorithm A is more efficient than alogrithm B.
B.For any problem in any scale, the alogorithm B is more efficient than alogrithm A.
C.As the scale of the proble increase,the alogrithm A is more efficient than alogrithm B.
D.As the scale of the proble increase,the alogrithm B is more efficient than alogrithm A.
👉Review Link🔗:http://t.csdnimg.cn/BNoOJ
所消耗的时间从小到大:
O(1)<O(logn)<O(n)<O(nlogn)<O(n^2)<O(n^3)<O(2^n)<O(n!)<O(n^n)
时间越小效率越高,所以A的效率高于B,---->选择C
栈的深入理解
2.Suppose 6 items pushed in the relative order like [6,5,4,3,2,1],which pop order is FALSE?
A.543612
B.453126
C.234156
D.346521
Review Link🔗:👉http://t.csdnimg.cn/LDWaR
进出栈无需一次性进完,一次性弹出.
可以进一个弹一个,也可以进几个,弹几个.
抓住栈的特点,先进后出,有进有出.




只要深入理解栈的知识点,我们通过画图或思考形式就可以做出这道题.
所以这题应该选D,因为5应该比6先出栈.
如何影响链表时间复杂度
3.There is an single Unordered Linked List with two head and rear pointers p and q, respectively. Which of the following operations time complexity that is affected by Linked List lengths
A. Deleting the head.
B. Deleting the rear.
C. Inserting new node to head.
D. Deleting node at rear.
Review Link🔗:👉http://t.csdnimg.cn/ET039
因为在无序链表中,删除后部需要从头节点开始遍历到尾节点,时间复杂度为O(n),n为链表长度。而其他操作只需要对头节点进行操作,时间复杂度不受链表长度的影响,几乎为O(1)。---> 选B,D
双端队列的深入理解
4.Suppose there is enqueue order "abcd' for a Deque (abcd' ehqueued at rear.) What's the possible dequue order for this Deque?
A. bdac
B. cadb
C. dbca
D. dacb
E. None of them is right.
Review Link🔗:👉
双端队列的入队顺序是:abcd,从尾部出,我们知道双端队列的特点就是两头都是可进可出的,但是不可以从中间出去. 所以逐项检验我们可得 ---> D是正确答案

📝Summary:
快速判断算法复杂度(适用于绝大多数简单情况)
确定问题规模n
循环减半过程一logn
k层关于n的循环一n
复杂情况:根据算法执行过程判断

What's the time complexity of the following code?(n is unknown, n > 10000).
i = 1
if i:while i < n:i = i * 3else:while i < n:i = i + 10The time complexity is O( ).
该代码的时间复杂度为O(logn)。因为第一个while循环中,i的值每次都会乘以3,直到i>=n为止,每次乘以3相当于对i进行了一次除法运算,假设n=i*3^k,则第一个while循环的迭代次数为log3(n),即O(logn)。第二个while循环中,i的值每次都会加上10,因此最多执行n/10次,影响可以忽略不计。因此,总的时间复杂度为O(logn)。

What's the time complexity of the following code ? (n is unknown, n > 10000)
i = 0
j = 0
while i < n:i += 1while j < n - i:j += 1该代码的时间复杂度为O(n^2)。外循环的执行次数为n,内循环的执行次数为(n-1)+(n-2)+...+1= (n-1)n/2,因此总的执行次数为n(n-1)*0.5,即O(n^2)。
i = 0
j = 0
while i < n:i += 1while j < n - i:j += 1j = 0时间复杂度为O(n^2)。外层循环i最多执行n次,内层循环j最多执行n-i次,因此总的执行次数为n*(n-1)/2,即O(n^2)。
本节主要讲的是算法中如何判断时间复杂度以及深入理解栈,双端队列的特点及应用.若想了解更多关于算法的内容,可以订阅我的算法专栏:http://t.csdnimg.cn/sof15
今天的干货分享到这里就结束啦!如果觉得文章还可以的话,希望能给个三连支持一下,Aileen的主页还有很多有趣的文章,欢迎小伙伴们前去点评,您的支持就我前进的最大动力!

相关文章:

【Python数据结构与算法】——(线性结构)精选好题分享,不挂科必看系列
🌈个人主页: Aileen_0v0🔥系列专栏:<<Python数据结构与算法专栏>>💫个人格言:"没有罗马,那就自己创造罗马~" 时间复杂度大小比较 1.time complexity of algorithm A is O(n^3) while algorithm B is O(2^n). Which o…...
)
大数据-之LibrA数据库系统告警处理(ALM-12054 证书文件失效)
告警解释 系统在每天二十三点检查当前系统中的证书文件是否失效(即当前集群中的证书文件是否过期,或者尚未生效)。如果证书文件失效,产生该告警。 当重新导入一个正常证书,并且状态不为失效状态,该告警恢…...

Linux 之 journalctl 查看系统与 kernel 日志
目录 1. Linux 之 journalctl 查看系统与 kernel 日志 1. Linux 之 journalctl 查看系统与 kernel 日志 1 概述 日志管理工具 journalctl 是 centos7 上专有的日志管理工具, 该工具是从 message 这个文件里读取信息。Systemd 统一管理所有 Unit 的启动日志。带来的好处就是, …...

【PTA题目】7-3 冰雹猜想。 分数 10
7-3 冰雹猜想。 分数 10 全屏浏览题目 切换布局 作者 赵静静 单位 浙江工贸职业技术学院 冰雹猜想的内容是:任何一个大于1的整数n,按照n为偶数则除等2,n为奇数则乘3后再加1的规则不断变化,最终都可以变化为1。 例如ÿ…...

springBoot 配置druid多数据源 MySQL+SQLSERVER
1:pom 文件引入数据 <dependency> <groupId>com.alibaba</groupId> <artifactId>druid-spring-boot-starter</artifactId> <version>1.1.0</version> </dependency>…...
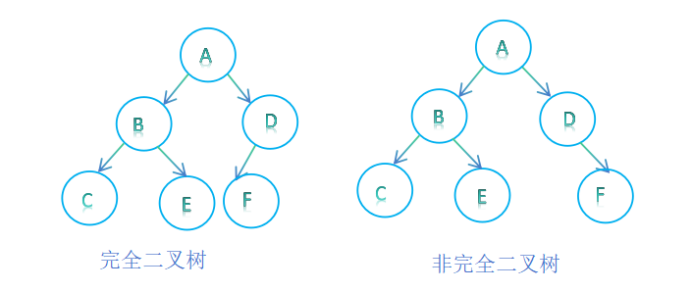
二叉树的创建与遍历
目录 前言: 二叉树的概念与结构 二叉树的链式存储 二叉树的创建 二叉树的销毁 二叉树结点个数计算 二叉树叶子结点个数计算 二叉树第k层节点个数的计算 二叉树高度的计算 二叉树查找值为x的结点 二叉树的遍历 二叉树的前序遍历 二叉树的中序遍历 二叉树…...

Mysql相关操作命令合集
参考文档:2021-06-25MySQL8.0创建用户和权限控制 - 简书 mysql登陆命令: mysql -u用户名 -p密码; 若遇到复杂密码,包含特殊字符,则需要做转义(以下密码为:rootry?elyl!): mysql…...
前端开发学习 (一) 搭建Vue基础环境
一、环境搭建 1、安装nodejs #下载地址 https://nodejs.org/dist/v20.9.0/node-v20.9.0-x64.msi 2、配置环境变量 上面下载完安装包后自行安装,安装完成后安装下图操作添加环境变量 #查看版本 node --version v20.9.0# npm --version 10.1.03、配置npm加速源 np…...

二维码智慧门牌管理系统升级解决方案:查询功能大提升,让地址查找变得轻松便捷!
文章目录 前言一、支持地址名称、小区等信息进行模糊查询二、支持地图上绘制多边形、圆形、矩形进行范围查询三、高效的数据处理能力,保证查询速度四、灵活的应用场景,满足多种需求 前言 随着科技的快速发展和城市化的加速推进,传统的门牌管…...
vite+vue3+electron开发环境搭建
环境 node 18.14.2 yarn 1.22 项目创建 yarn create vite test01安装vue环境 cd test01 yarn yarn dev说明vue环境搭建成功 安装electron # 因为有的版本会报错所以指定了版本 yarn add electron26.1.0 -D安装vite-plugin-electron yarn add -D vite-plugin-electron根目…...
:多态介绍与代码演示)
C#入门(9):多态介绍与代码演示
多态性是面向对象编程的一个核心概念,它允许你使用一个父类引用来指向一个子类对象。这可以使程序具有可扩展性,并且可以用来实现一些高级编程技术,如接口、事件、抽象类等。 多态相关的概念 以下是一些在C#中使用多态性的关键概念…...

可拖动、可靠边的 popupWindow 实现
0 背景 开发要实现一个可以拖动的圆角小窗,要求松手时,哪边近些靠哪边。并且还规定了拖动范围。样式如下: 1 实现 首先把 PopupWindow 的布局文件 pop.xml 实现 <?xml version"1.0" encoding"utf-8"?> <R…...

C# 依赖注入如何实现
在 C# 中,依赖注入(Dependency Injection,简称 DI)是一种编程技术,用于减少代码之间的耦合。依赖注入可以通过构造函数注入、属性注入或方法注入实现。在 .NET Core 和 .NET 5 中,还提供了一个内置的依赖注…...
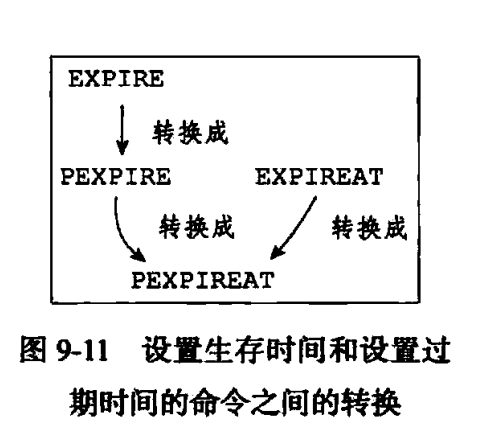
Redis 9 数据库
4 设置键的生存时间或过期时间 通过EXPIRE命令或者PEXPIRE命令,客户端可以以秒或者毫秒精度为数据库中的某个键设置生存时间(TimeToLive,TTL),在经过指定的秒数或者毫秒数之后,服务器就会自动删除生存时间…...

43-设计问题-最小栈
原题链接: 198. 打家劫舍 题目描述: 你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入&a…...
基于RK3588全高端智能终端机器人主板
一、小尺寸板型设计 该款主板为小型板,尺寸仅为125*85mm,更小更紧凑,可完美适应各类高端智能自助终端; 二、八核高端处理器 采用RK3588S八核64位处理器,8nm LP制程,主频最高达2.4GHz,搭载Andr…...
穿越风波,“长红”的直播电商依然扎根产业和消费者
当消费者将最后一个快递拿进家门,2023年的双11也就落下了帷幕。相较于往年组队、拼单的玩法,如今最受欢迎的双11 流程,或许已经变成点进自己心仪主播、店铺的直播间,翻阅最新的产品清单,从中选择购物目标,在…...
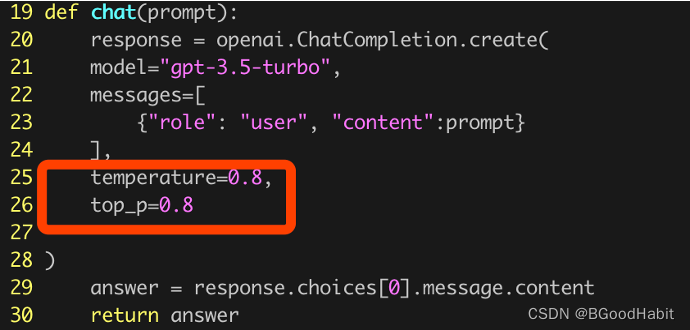
LLM大模型 (chatgpt) 在搜索和推荐上的应用
目录 1 大模型在搜索的应用1.1 召回1.1.1 倒排索引1.1.2 倒排索引存在的问题1.1.3 大模型在搜索召回的应用 (实体倒排索引) 1.2 排序1.2.1 大模型在搜索排序应用(融入LLM实体排序) 2 大模型在推荐的应用2.1 学术界关于大模型在推荐的研究2.2 …...

中国净初级生产力年度合成产品NPP(MYD17A3H.006)
中国净初级生产力年度合成产品NPP(MYD17A3H.006)由航天宏图实验室提供,根据NASA MODIS数据(MYD17A3H.006)通过航天宏图 Smoother计算得到的平滑后NPP产品,解决了影像云雾覆盖、像元异常值等问题。对处理后的…...
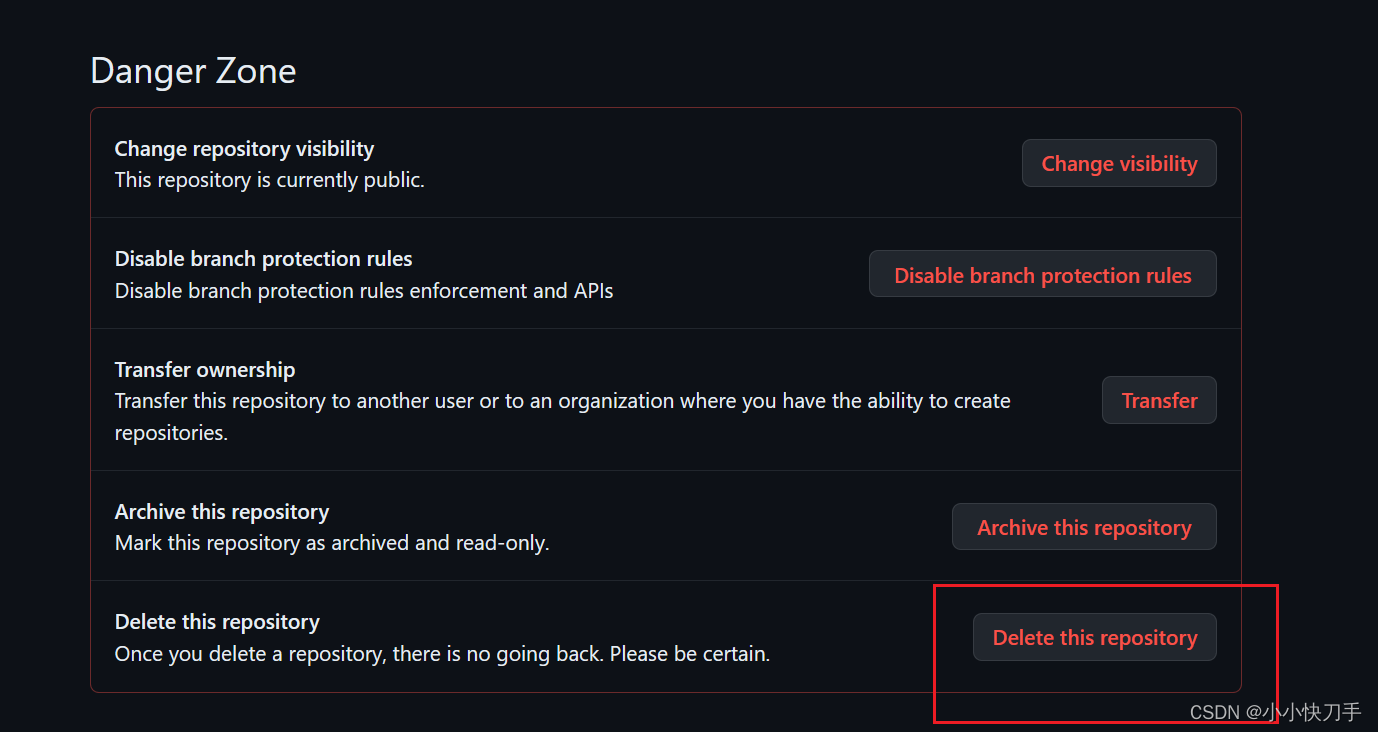
GitHub如何删除仓库
GitHub如何删除仓库 删除方法第一步第二步第三步 删除方法 第一步 在仓库的界面选择Settings 第二步 选择General,页面拉到最后。 第三步 删除仓库。...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...
