二叉树的创建与遍历
目录
前言:
二叉树的概念与结构
二叉树的链式存储
二叉树的创建
二叉树的销毁
二叉树结点个数计算
二叉树叶子结点个数计算
二叉树第k层节点个数的计算
二叉树高度的计算
二叉树查找值为x的结点
二叉树的遍历
二叉树的前序遍历
二叉树的中序遍历
二叉树的后序遍历
二叉树的层序遍历
判断二叉树是否为完全二叉树
前言:
二叉树的层序遍历需要使用队列实现,队列的实现见数据结构之队列,对于二叉树的代码,需要不断画递归展开图进行结合理解,递归展开图不展开描述;
二叉树的概念与结构
一棵二叉树是n个有限结点的集合,该集合或者为空,或者由一个称为根(root)的结点或者由一个根结点加上两棵别称为左子树和右子树的二叉树组成 ;
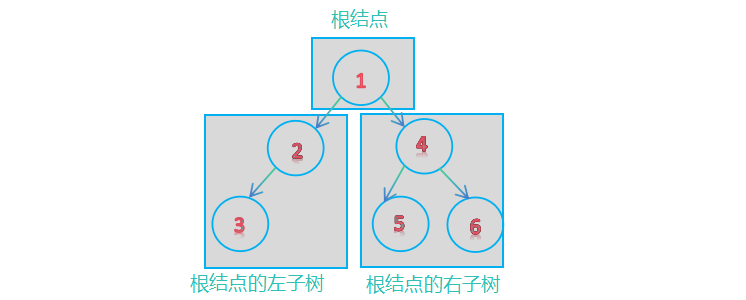
二叉树的链式存储
二叉树的链式存储结构指的是用链表表示一棵二叉树,即用链表指示元素的逻辑关系;
通常的方法是链表中每个结点由三个域组成,数据域与左右指针域,左右指针分别用来给出该结点左孩子和右孩子所在的链结点的存储地址;
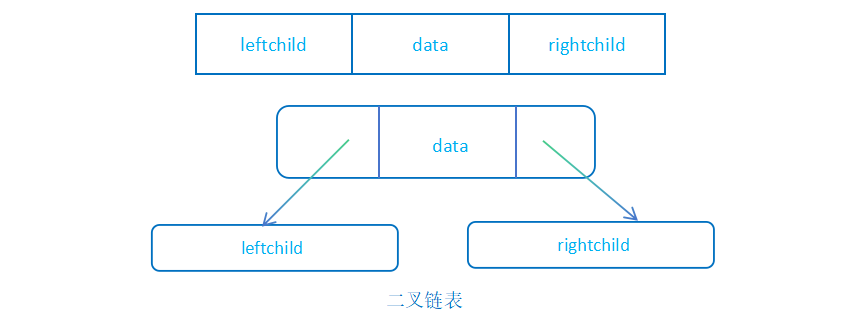
二叉树的创建
扩展二叉树是指在二叉树中出现空子树的位置增加空树叶,所形成的二叉树,使得子树成为满二叉树的二叉树叫做扩展二叉树;
先序遍历字符串 A B C # # # D # # 其中“#”表示的是空格,空格字符代表空树,则建立起来的二叉树如下图所示:
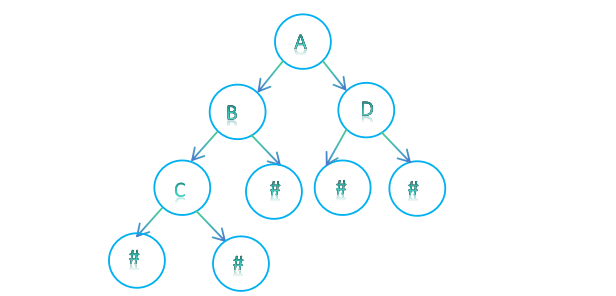
//二叉树结点结构
typedef int BTDataType;
typedef struct BinaryTreeNode
{struct BinaryTreeNode* left;struct BinaryTreeNode* right;BTDataType val;
}BTNode;//创建二叉树,返回根结点地址
//A B C # # # D # #
BTNode* CreateTree(char* str, int* pi)
{if (str[*pi] == '#'){(*pi)++;return NULL;}BTNode* root = (BTNode*)malloc(sizeof(BTNode));root->val = str[*pi];(*pi)++;root->left = CreateTree(str, pi);root->right = CreateTree(str, pi);return root;}
int main()
{char arr[100] = { 'A', 'B', 'C', '#', '#', '#', 'D', '#', '#' };int i = 0;BTNode* root = CreateTree(arr, &i);return 0;
}二叉树的销毁
按照先销毁其左子树,再销毁右子树,最后销毁根的顺序递归销毁二叉树;
void DestroyTree(BTNode* root)
{if (root == NULL)return;DestroyTree(root->left);DestroyTree(root->right);free(root);
}二叉树结点个数计算
若根结点为空,则二叉树结点个数=0;
若根节点不为空,则二叉树结点个数=左子树的结点个数+右子树极点个数+1;
//二叉树结点个数
int TreeSize(BTNode* root)
{if (root == NULL)return 0;return TreeSize(root->left) + TreeSize(root->right) + 1;
}二叉树叶子结点个数计算
叶子结点即某一节点出的左孩子为空并且右孩子为空则为叶子结点;
//二叉树叶子结点个数
int TreeLeafSize(BTNode* root)
{if (root == NULL)return 0;if (root->left == NULL && root->right == NULL)return 1;return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}二叉树第k层节点个数的计算
规定:二叉树的层数K以1为起点,即第一层 k = 1;
二叉树的第k层节点个数=其左子树的第k-1层节点个数+其右子树的第k-1层节点个数;
int TreeKLevel(BTNode* root,int k)
{assert(k > 0);if (root == NULL)return 0;if (k == 1)return 1;return TreeKLevel(root->left, k - 1) + TreeKLevel(root->right, k - 1);
}二叉树高度的计算
二叉树的高度=左子树的高度与右子树的高度较大值+1;
//二叉树的高度
int TreeHeight(BTNode* root)
{if (root == NULL)return 0;int LeftHeight = TreeHeight(root->left);int RightHeight = TreeHeight(root->right);return LeftHeight > RightHeight ? LeftHeight + 1 : RightHeight + 1;
}二叉树查找值为x的结点
如根节点非空,先查找根,如果根结点处的值即为查找的值,直接返回根节点的地址,如果根节点处未查找到,先查找左子树,找到了直接返回,找不到继续查找右子树;
//二叉树查找值为x的结点
BTNode* TreeFind(BTNode* root, BTDataType x)
{if (root == NULL)return NULL;if (root->val == x)return root;struct BinaryTreeNode* ret = NULL;ret = TreeFind(root->left, x);if (ret != NULL)return ret;ret = TreeFind(root->right, x);if (ret != NULL)return ret;return NULL;
}二叉树的遍历
- 前序遍历NLR(依次遍历:根结点—左子树—右子树)
- 中序遍历LNR(依次遍历:左子树—根结点—右子树)
- 后序遍历LRN(依次遍历:左子树—右子树—根结点)
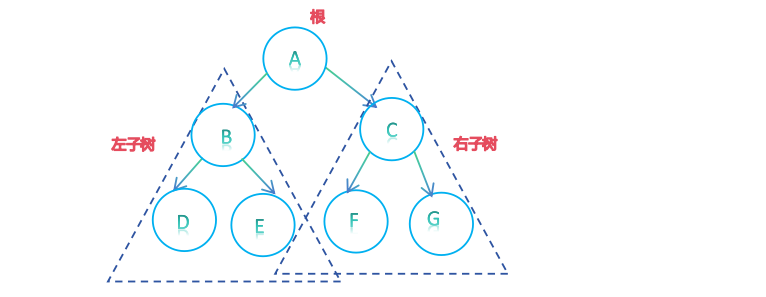
由于二叉树是递归定义的,按照下图所示方法,便可得到前序遍历的结点顺序
前序遍历结果:A->B->D->E->C->F->G
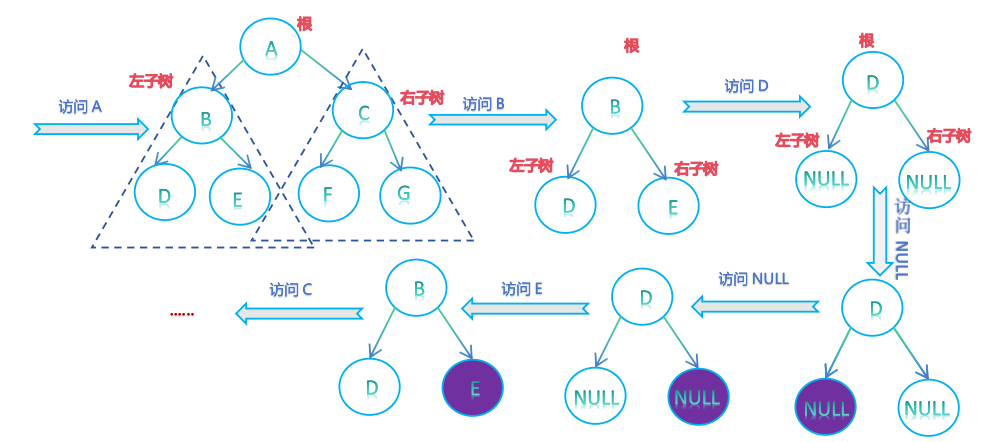
中序遍历结果为D->B->E->A->F->C->G;后序遍历结果:D->E->B->F->G->C->A;
二叉树的前序遍历
//二叉树的前序遍历
void PrevOrder(BTNode* root)
{if (root == NULL)return;printf("%c ", root->val);PrevOrder(root->left);PrevOrder(root->right);
}二叉树的中序遍历
//二叉树的中序遍历
void InOrder(BTNode* root)
{if (root == NULL)return;InOrder(root->left);printf("%c ", root->val);InOrder(root->right);
}二叉树的后序遍历
//二叉树的后序遍历
void PostOrder(BTNode* root)
{if (root == NULL)return;PostOrder(root->left);PostOrder(root->right);printf("%c ", root->val);
}二叉树的层序遍历
二叉树的层序遍历是指将二叉树从上到下,从左到右依次遍历,如下图所示层序遍历结果为
A—>B—>D—>C
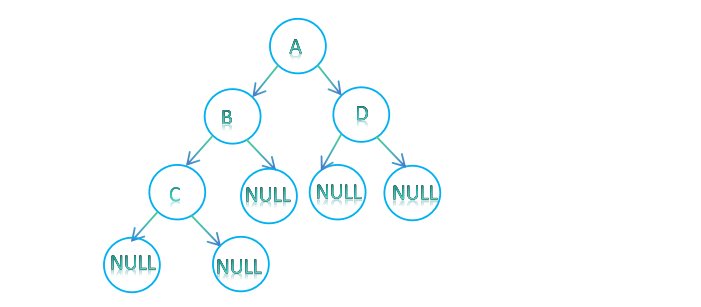
层序遍历的思路如下:
1. 判断根结点是否为空,非空则入队列
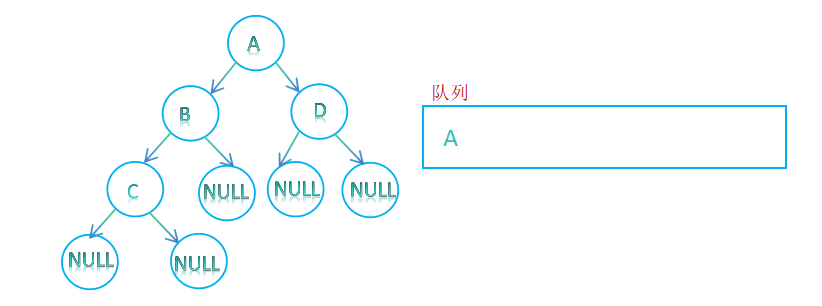
2. 判断队列是否为空,不为空则队头元素出队列,再将队头元素的孩子入队列,若队头元素的孩子为空,则不入队列;
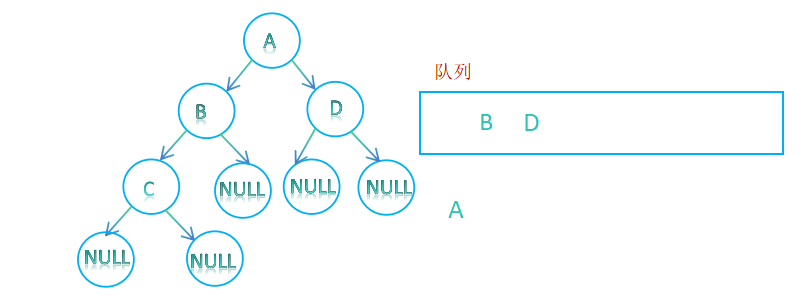
3.判断队列是否为空,将B出队列,再将B的孩子入队列;
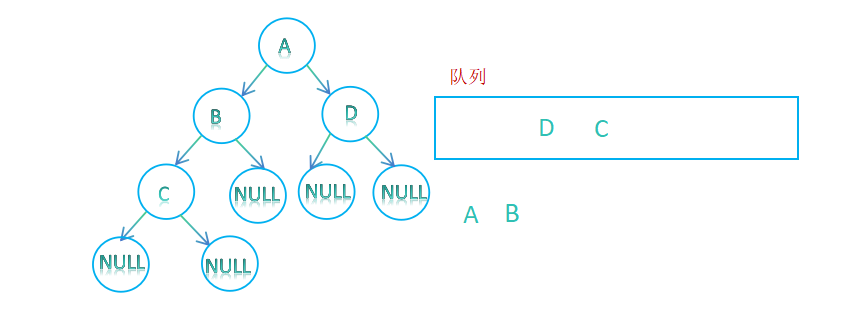
4.判断队列是否为空,将D出队列,再将D的孩子入队列;
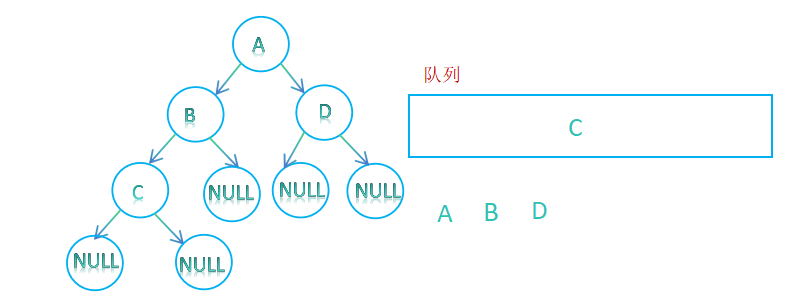
5. 判断队列是否为空,将C出队列,再将C的孩子入队列;队列为空时结束遍历;
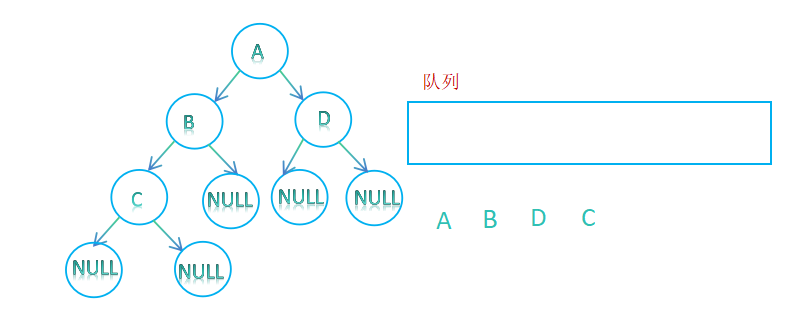
//二叉树的层序遍历
void BinaryTreeLevelOrder(BTNode* root)
{Queue q;InitQueue(&q);if (root != NULL)QueuePush(&q, root);while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);printf("%c ", front->val);if (front->left != NULL);QueuePush(&q, front->left);if (front->right != NULL)QueuePush(&q, front->right);QueuePop(&q);}DestroyQueue(&q);
}
判断二叉树是否为完全二叉树
满二叉树:当二叉树深度为K,二叉树结点个数为2^k-1,则为满二叉树;
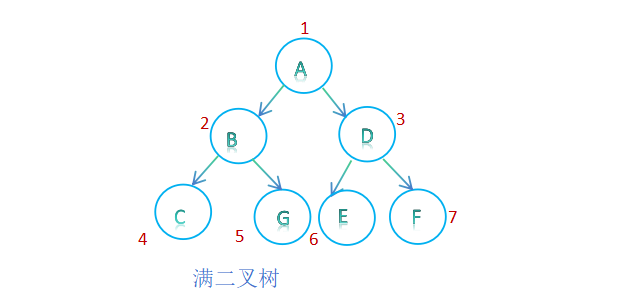
对满二叉树结点位置进行编号
- 编号的规则:自上而下,从左向右 ;
- 每一节点位置都有元素;
完全二叉树
深度为K具有n个结点的二叉树,当且仅当其每一个节点都与深度为k的满二叉树中的编号为1~n的节点一 一对应时,称为完全二叉树;
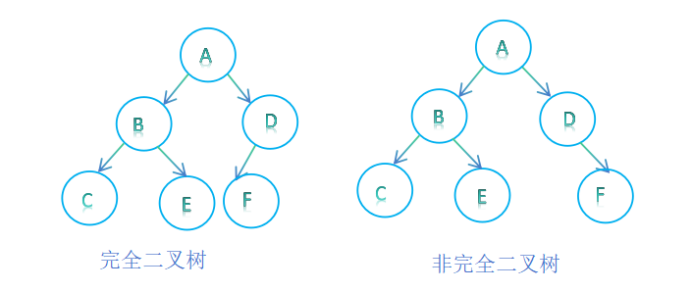
判断二叉树是否是完全二叉树,是完全二叉树返回true,否则返回false;
利用二叉树层序遍历,非空结点连续为完全二叉树,非空结点不连续,存在空节点,则为非完全二叉树;
int BinaryTreeComplete(BTNode* root)
{Queue q;InitQueue(&q);if (root != NULL)QueuePush(&q, root);while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);if (front == NULL)break;QueuePush(&q, front->left);QueuePush(&q, front->right);QueuePop(&q);}//若已经出现空结点,队列后面结点存在非空结点,则为非完全二叉树while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);if (front != NULL){DestroyQueue(&q);return false;}}DestroyQueue(&q);return true;
}相关文章:

二叉树的创建与遍历
目录 前言: 二叉树的概念与结构 二叉树的链式存储 二叉树的创建 二叉树的销毁 二叉树结点个数计算 二叉树叶子结点个数计算 二叉树第k层节点个数的计算 二叉树高度的计算 二叉树查找值为x的结点 二叉树的遍历 二叉树的前序遍历 二叉树的中序遍历 二叉树…...

Mysql相关操作命令合集
参考文档:2021-06-25MySQL8.0创建用户和权限控制 - 简书 mysql登陆命令: mysql -u用户名 -p密码; 若遇到复杂密码,包含特殊字符,则需要做转义(以下密码为:rootry?elyl!): mysql…...
前端开发学习 (一) 搭建Vue基础环境
一、环境搭建 1、安装nodejs #下载地址 https://nodejs.org/dist/v20.9.0/node-v20.9.0-x64.msi 2、配置环境变量 上面下载完安装包后自行安装,安装完成后安装下图操作添加环境变量 #查看版本 node --version v20.9.0# npm --version 10.1.03、配置npm加速源 np…...

二维码智慧门牌管理系统升级解决方案:查询功能大提升,让地址查找变得轻松便捷!
文章目录 前言一、支持地址名称、小区等信息进行模糊查询二、支持地图上绘制多边形、圆形、矩形进行范围查询三、高效的数据处理能力,保证查询速度四、灵活的应用场景,满足多种需求 前言 随着科技的快速发展和城市化的加速推进,传统的门牌管…...
vite+vue3+electron开发环境搭建
环境 node 18.14.2 yarn 1.22 项目创建 yarn create vite test01安装vue环境 cd test01 yarn yarn dev说明vue环境搭建成功 安装electron # 因为有的版本会报错所以指定了版本 yarn add electron26.1.0 -D安装vite-plugin-electron yarn add -D vite-plugin-electron根目…...
:多态介绍与代码演示)
C#入门(9):多态介绍与代码演示
多态性是面向对象编程的一个核心概念,它允许你使用一个父类引用来指向一个子类对象。这可以使程序具有可扩展性,并且可以用来实现一些高级编程技术,如接口、事件、抽象类等。 多态相关的概念 以下是一些在C#中使用多态性的关键概念…...

可拖动、可靠边的 popupWindow 实现
0 背景 开发要实现一个可以拖动的圆角小窗,要求松手时,哪边近些靠哪边。并且还规定了拖动范围。样式如下: 1 实现 首先把 PopupWindow 的布局文件 pop.xml 实现 <?xml version"1.0" encoding"utf-8"?> <R…...

C# 依赖注入如何实现
在 C# 中,依赖注入(Dependency Injection,简称 DI)是一种编程技术,用于减少代码之间的耦合。依赖注入可以通过构造函数注入、属性注入或方法注入实现。在 .NET Core 和 .NET 5 中,还提供了一个内置的依赖注…...
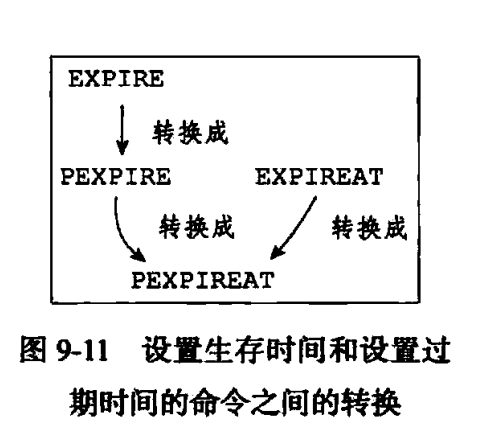
Redis 9 数据库
4 设置键的生存时间或过期时间 通过EXPIRE命令或者PEXPIRE命令,客户端可以以秒或者毫秒精度为数据库中的某个键设置生存时间(TimeToLive,TTL),在经过指定的秒数或者毫秒数之后,服务器就会自动删除生存时间…...

43-设计问题-最小栈
原题链接: 198. 打家劫舍 题目描述: 你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入&a…...
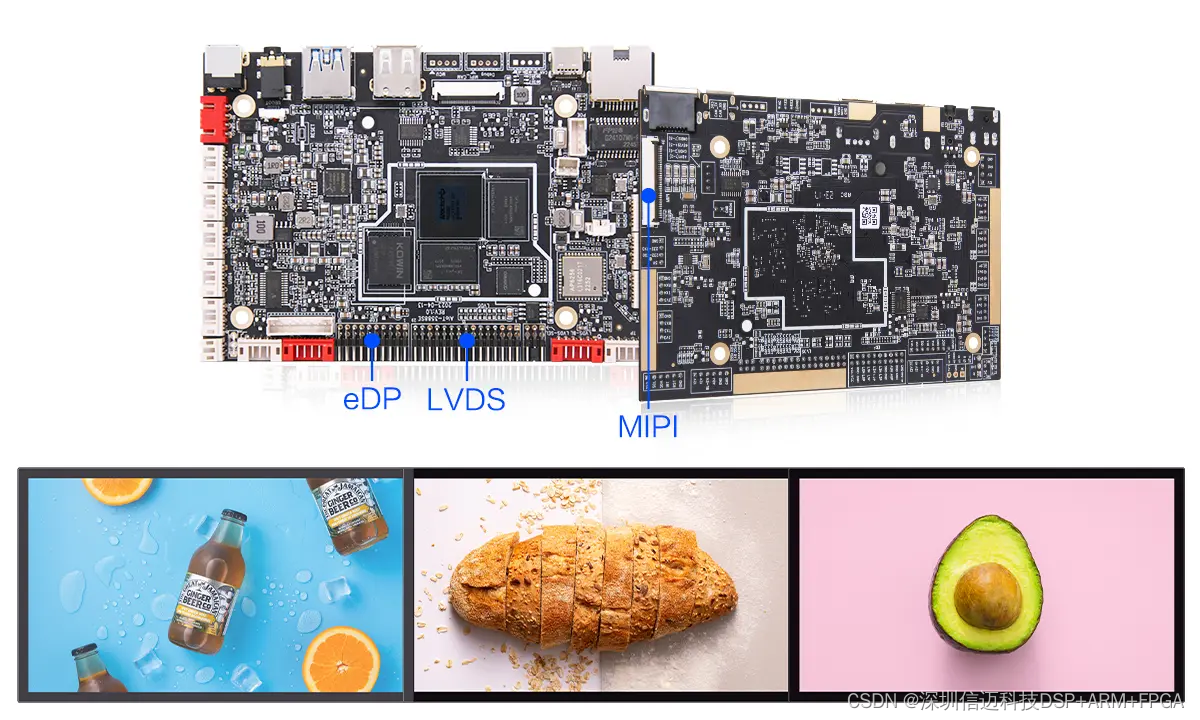
基于RK3588全高端智能终端机器人主板
一、小尺寸板型设计 该款主板为小型板,尺寸仅为125*85mm,更小更紧凑,可完美适应各类高端智能自助终端; 二、八核高端处理器 采用RK3588S八核64位处理器,8nm LP制程,主频最高达2.4GHz,搭载Andr…...
穿越风波,“长红”的直播电商依然扎根产业和消费者
当消费者将最后一个快递拿进家门,2023年的双11也就落下了帷幕。相较于往年组队、拼单的玩法,如今最受欢迎的双11 流程,或许已经变成点进自己心仪主播、店铺的直播间,翻阅最新的产品清单,从中选择购物目标,在…...
LLM大模型 (chatgpt) 在搜索和推荐上的应用
目录 1 大模型在搜索的应用1.1 召回1.1.1 倒排索引1.1.2 倒排索引存在的问题1.1.3 大模型在搜索召回的应用 (实体倒排索引) 1.2 排序1.2.1 大模型在搜索排序应用(融入LLM实体排序) 2 大模型在推荐的应用2.1 学术界关于大模型在推荐的研究2.2 …...

中国净初级生产力年度合成产品NPP(MYD17A3H.006)
中国净初级生产力年度合成产品NPP(MYD17A3H.006)由航天宏图实验室提供,根据NASA MODIS数据(MYD17A3H.006)通过航天宏图 Smoother计算得到的平滑后NPP产品,解决了影像云雾覆盖、像元异常值等问题。对处理后的…...
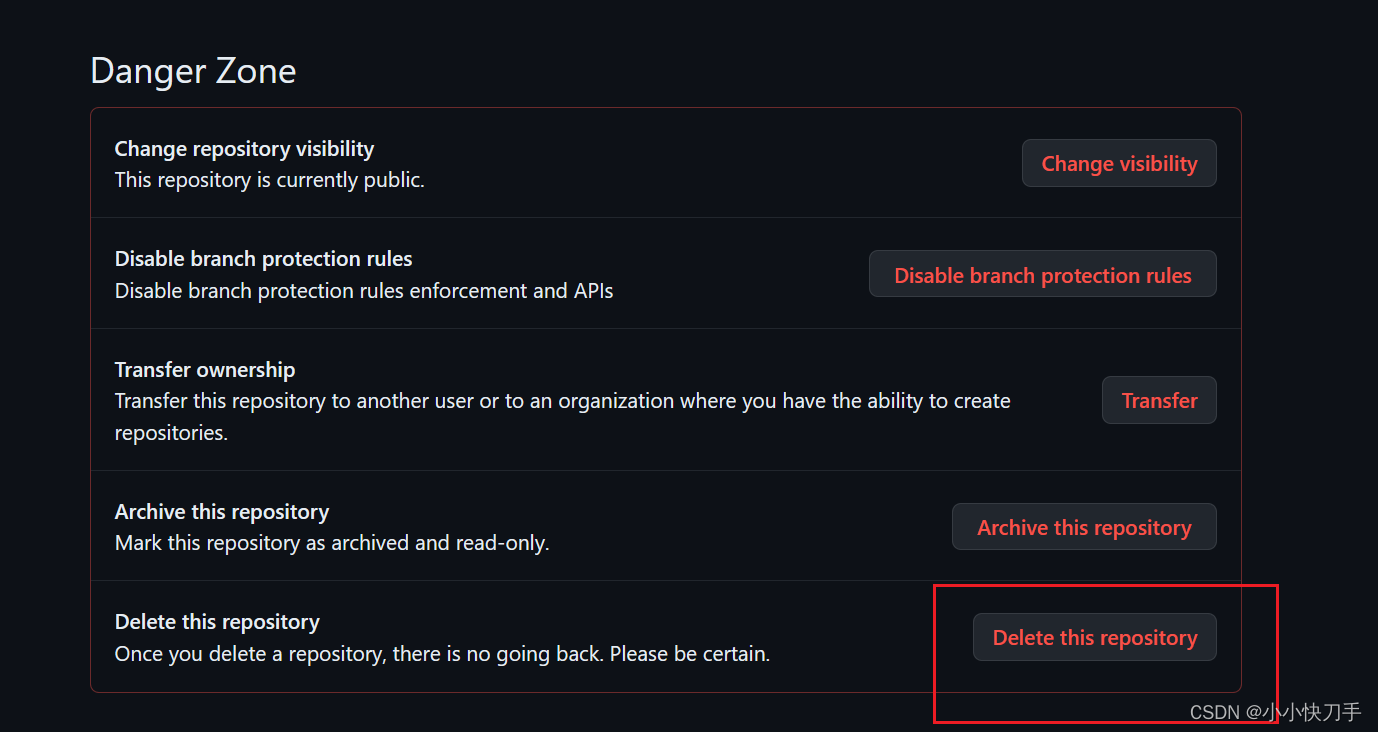
GitHub如何删除仓库
GitHub如何删除仓库 删除方法第一步第二步第三步 删除方法 第一步 在仓库的界面选择Settings 第二步 选择General,页面拉到最后。 第三步 删除仓库。...

漫谈广告机制设计 | 万剑归宗:聊聊广告机制设计与收入提升的秘密(3)
书接上文漫谈广告机制设计 | 万剑归宗:聊聊广告机制设计与收入提升的秘密(2),我们聊到囚徒困境是完全信息静态博弈,参与人存在占优策略,最终达到占优均衡,并且是对称占优均衡。接下来我们继续…...

安装系统时无raid驱动处理办法
场景描述 安装系统时可以进入安装界面,但是无法识别到硬盘,查看服务器硬件均无异常且从bios或者raid配置界面中能正常看到raid信息及硬盘信息,运行lspci 命令查看到服务器有raid卡,但是未加载驱动。 获取驱动程序模块 查看raid…...
ForkLift:macOS文件管理器/FTP客户端
ForkLift 是一款macOS下双窗口的文件管理器,可以代替本地的访达。ForkLift同时具备连接Ftp、SFtp、WebDav以及云服务器。 ForkLift还具备访达不具备的小功能,比如从文件夹位置打开终端,显示隐藏文件,制作替换等功能。ForkLift 是一…...

信息系统项目管理师 第四版 第20章 高级项目管理
1.项目集管理 1.1.项目集管理标准 1.2.项目集管理角色和职责 1.3.项目集管理绩效域 2.项目组合管理 2.1.项目组合管理标准 2.2.项目组合管理角色和职责 2.3.项目组合管理绩效域 3.组织级项目管理 3.1.组织级项目管理标准 3.2.业务价值与业务评估 3.3.OPM框架要素 3…...
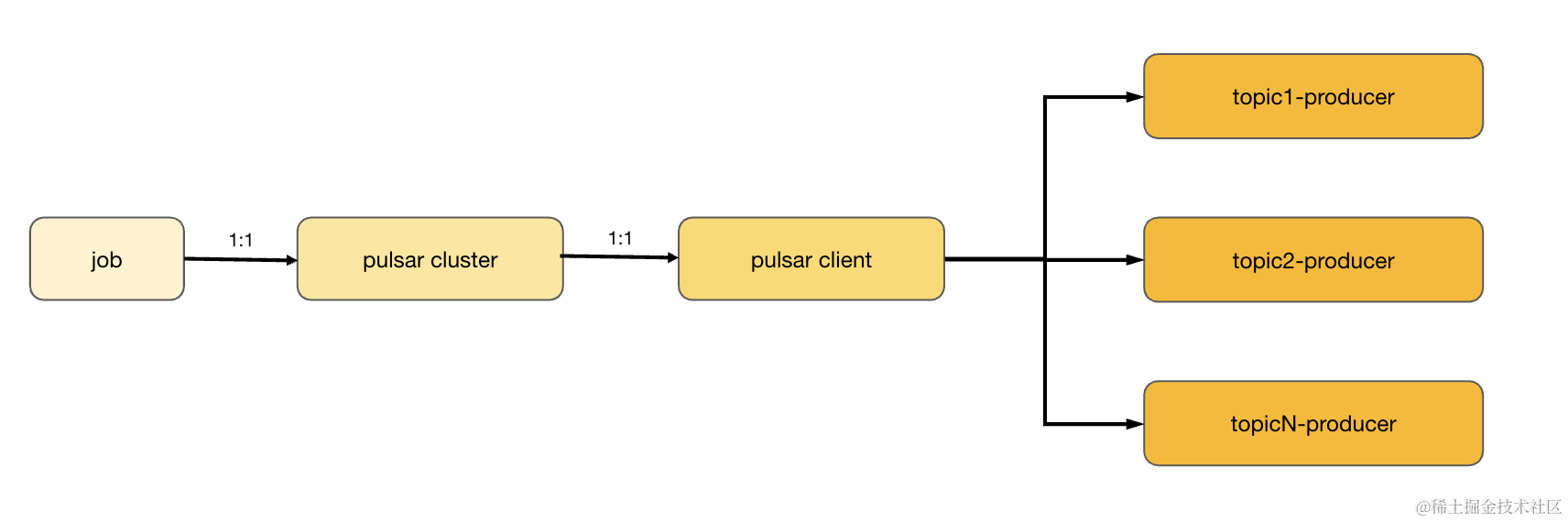
Apache Pulsar 技术系列 - 基于 Pulsar 的海量 DB 数据采集和分拣
导语 Apache Pulsar 是一个多租户、高性能的服务间消息传输解决方案,支持多租户、低延时、读写分离、跨地域复制、快速扩容、灵活容错等特性。本文是 Pulsar 技术系列中的一篇,主要介绍 Pulsar 在海量DB Binlog 增量数据采集、分拣场景下的应用。 前言…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...

热门Chrome扩展程序存在明文传输风险,用户隐私安全受威胁
赛门铁克威胁猎手团队最新报告披露,数款拥有数百万活跃用户的Chrome扩展程序正在通过未加密的HTTP连接静默泄露用户敏感数据,严重威胁用户隐私安全。 知名扩展程序存在明文传输风险 尽管宣称提供安全浏览、数据分析或便捷界面等功能,但SEMR…...

客户案例 | 短视频点播企业海外视频加速与成本优化:MediaPackage+Cloudfront 技术重构实践
01技术背景与业务挑战 某短视频点播企业深耕国内用户市场,但其后台应用系统部署于东南亚印尼 IDC 机房。 随着业务规模扩大,传统架构已较难满足当前企业发展的需求,企业面临着三重挑战: ① 业务:国内用户访问海外服…...

云原生安全实战:API网关Envoy的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关 作为微服务架构的统一入口,负责路由转发、安全控制、流量管理等核心功能。 2. Envoy 由Lyft开源的高性能云原生…...

【Ftrace 专栏】Ftrace 参考博文
ftrace、perf、bcc、bpftrace、ply、simple_perf的使用Ftrace 基本用法Linux 利用 ftrace 分析内核调用如何利用ftrace精确跟踪特定进程调度信息使用 ftrace 进行追踪延迟Linux-培训笔记-ftracehttps://www.kernel.org/doc/html/v4.18/trace/events.htmlhttps://blog.csdn.net/…...
