二元关系及关系代数中的象集、除运算
二元关系及关系代数中的象集、除运算
数学上,二元关系用于讨论两个数学对象的联系。诸如算术中的「大于」及「等于」,几何学中的"相似",或集合论中的"为...之元素"或"为...之子集"。二元关系有时会简称关系,但一般而言关系不必是二元的。
【集合论】二元关系 ( 定义域 | 值域 | 域 | 逆运算 | 逆序合成运算 | 限制 | 像 | 单根 | 单值 | 合成运算的性质 )_c++实现二元关系逆运算-CSDN博客
定义
集合X与集合Y上的二元关系是R=(X,Y,G(R)),其中G(R),称为R的图,是笛卡儿积X×Y的子集。若 (x,y) ∈G(R) ,则称x是R-关系于y,并记作xRy或R(x,y)。否则称x与y无关系R。但经常地我们把关系与其图等同起来,即:若R⊆X×Y,则R是一个关系。
例如:有四件物件 {球,糖,车,枪} 及四个人 {甲,乙,丙,丁}。 若甲拥有球,乙拥有糖,及丁拥有车,即无人有枪及丙一无所有— 则二元关系"为...拥有"便是R=({球,糖,车,枪}, {甲,乙,丙,丁}, {(球,甲), (糖,乙), (车,丁)})。
其中 R 的首项是物件的集合,次项是人的集合,而末项是由有序对(物件,主人)组成的集合。比如有序对(球,甲)∈G(R),所以我们可写作"球R甲",表示球为甲所拥有。
不同的关系可以有相同的图。以下的关系 ({球,糖,车,枪}, {甲,乙,丁}, {(球,甲), (糖,乙), (车,丁)} 中人人皆是物主,所以与R不同,但两者有相同的图。话虽如此,我们很多时候索性把R定义为G(R), 而 "有序对 (x,y) ∈G(R)" 亦即是 "(x,y) ∈R"。
二元关系可看作成二元函数,这种二元函数把输入元x∈X及y∈Y视为独立变量并求真伪值(即“有序对(x,y) 是或非二元关系中的一元”此一问题)。
若X=Y,则称R为X上的关系。
特殊的二元关系
注:下文我们将采用把二元关系R定义为A × A的子集的做法。
设A是一个集合,则:
空集∅称作A上的空关系(因为∅也是A × A的子集)。
EA = A × A称作A上的全域关系。
IA = {(x,,x): x∈A} 称作A上的恒等关系。
例1:
设A={1,2,3},R1,R2和R3是A上的关系,其中:R1={<1,1>,<2,2>};R2={<1,1>,<2,2>,<3,3>,<1,2>};R3={<1,3>},则R1不是自反的,R3是反自反的,R2是自反的但不是反自反的。
例2:
设A={1,2,3},R1,R2,R3和R4是A上的关系,其中:R1={<1,1>,<2,2>};R2={<1,1>,<1,2>,<2,1>};R3={<1,2>,<1,3>};R4={<1,2>,<2,1>,<1,3>},则R1既是对称的也是反对称的。R2是对称的但不是反对称的。R3是反对称的但不是对称的。R4既不是对称的也不是反对称的。
例3:
设A={1,2,3},R1,R2和R3是A上的关系,其中:R1={<1,1>,<2,2>};R2={<1,2>,<2,3>};R3={<1,3>},则R1和R3是A上的传递关系,R2不是A上的传递关系。
【数据库】解释关系代数中的象集、除运算-CSDN博客
相关文章:

二元关系及关系代数中的象集、除运算
二元关系及关系代数中的象集、除运算 数学上,二元关系用于讨论两个数学对象的联系。诸如算术中的「大于」及「等于」,几何学中的"相似",或集合论中的"为...之元素"或"为...之子集"。二元关系有时会简称关系&a…...

[PHP]关联和操作MySQL数据库然后将数据库部署到ECS
在Mac电脑上使用VS Code进行PHP开发并关联操作MySQL数据库,然后将数据库部署到ECS。 1.安装PHP和MySQL 确保你的Mac上已经安装了PHP和MySQL。你可以使用Homebrew来安装它们: $ brew install php $ brew install mysql 安装mysql完成后记住这一句: …...

23.11.19日总结
经过昨天的中期答辩,其实可以看出来项目进度太慢了,现在是第十周,预计第十四周是终级答辩,在这段时间要把项目写完。 前端要加上一个未登录的拦截器,后端加上全局的异常处理。对于饿了么项目的商品建表,之前…...

系列一、JVM概述
一、概述 1.1、Java发展中的重大事件 1.2、虚拟机 vs Java虚拟机 1.2.1、虚拟机 1.2.2、Java虚拟机 1.2.3、Java虚拟机的作用 Java虚拟机是二进制字节码的运行环境,负责装载字节码到其内部,解释/编译为对应平台上的机器指令指令。每一条Java指令&#…...

milvus数据管理-压缩数据
Milvus 默认支持自动数据压缩。您可以 配置 Milvus 以启用或禁用 压缩 和自动压缩。 如果自动压缩被禁用,您仍然可以手动压缩数据。 1.手动压缩数据 压缩请求是异步处理的,因为它们通常需要花费很长时间。 from pymilvus import Collection collection…...

SpringBoot项目连接linux服务器数据库两种解决方法(linux直接开放端口访问本机通过SSH协议访问,以mysql为例)
最近找个springboot脚手架重新熟悉一下springboot相关框架的东西,结果发现好像项目还不能直接像数据库GUI工具一样填几个SSH参数就可以了,于是就给他再整一下看看如何解决 linux开放3306(可修改)端口直接访问 此方法较为方便&am…...

【Rust】快速教程——闭包与生命周期
前言 你怎么向天生的瞎子说清颜色?怎么用手势向天生的聋子描述声音? 鲜花就在眼前,雷鸣就在头顶,对他们来说却都毫无意义 眼睛看不到,鼻子可以嗅闻花香,耳朵听不见,手指可以触碰窗纸的震动。 犯…...
redis高级案列case
案列一 双写一致性 案例二 双锁策略 package com.redis.redis01.service;import com.redis.redis01.bean.RedisBs; import com.redis.redis01.mapper.RedisBsMapper; import lombok.extern.slf4j.Slf4j; import org.springframework.beans.factory.annotation.Autowired; imp…...

Vue3+Vite实现工程化,attribute属性渲染v-bind指令
想要渲染一个元素的attribute,应该使用v-bind指令 由于插值表达式不能直接放在标签的属性中,所有要渲染元素的属性就应该使用v-bindv-bind可以用于渲染任何元素的属性,语法为 v-bind:属性名数据名,可以简写为 :属性名数据名 <…...
下一代搜索引擎会什么?
现在是北京时间2023年11月18日。聊一聊搜索。 说到搜索,大家首先想到的肯定是谷歌,百度。我把这些定义成上一个时代的搜索引擎。ChatGPT已经火热了有一年的时间了,大家都认为Ai搜索是下一代的搜索。但是AI搜索,需要的是很大算力&a…...

WPF中如何在MVVM模式下关闭窗口
完全来源于十月的寒流,感谢大佬讲解 使用Behaviors <Window x:Class"Test_03.MainWindow"xmlns"http://schemas.microsoft.com/winfx/2006/xaml/presentation"xmlns:b"http://schemas.microsoft.com/xaml/behaviors"xmlns:x&quo…...
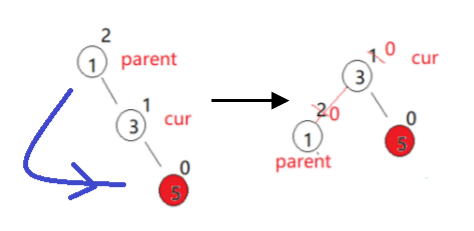
【数据结构&C++】二叉平衡搜索树-AVL树(25)
前言 大家好吖,欢迎来到 YY 滴C系列 ,热烈欢迎! 本章主要内容面向接触过C的老铁 主要内容含: 欢迎订阅 YY滴C专栏!更多干货持续更新!以下是传送门! 目录 一.AVL树的概念二.AVL树节点的定义(代码…...

Python算法——树的最大深度和最小深度
Python中的树的最大深度和最小深度算法详解 树的最大深度和最小深度是树结构中的两个关键指标,它们分别表示树的从根节点到最深叶子节点的最大路径长度和最小路径长度。在本文中,我们将深入讨论如何计算树的最大深度和最小深度,并提供Python…...

46.全排列-py
46.全排列 class Solution(object):def permute(self, nums):""":type nums: List[int]:rtype: List[List[int]]"""# 结果数组0ans[]nlen(nums)# 判断是否使用state_[False]*n# 临时状态数组dp_[]def dfs (index):# 终止条件if indexn:ans.appe…...
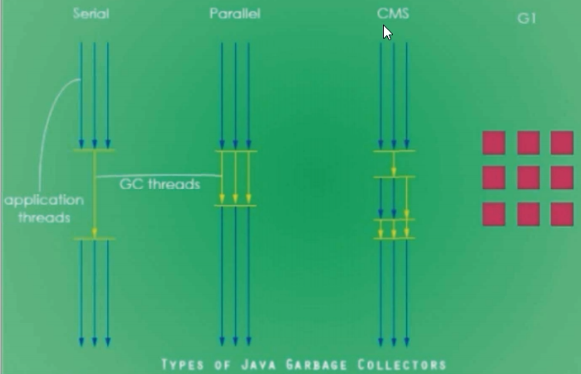
系列三、GC垃圾回收算法和垃圾收集器的关系?分别是什么请你谈谈
一、关系 GC算法(引用计数法、复制算法、标记清除算法、标记整理算法)是方法论,垃圾收集器是算法的落地实现。 二、4种主要垃圾收集器 4.1、串行垃圾收集器(Serial) 它为单线程环境设计,并且只使用一个线程…...
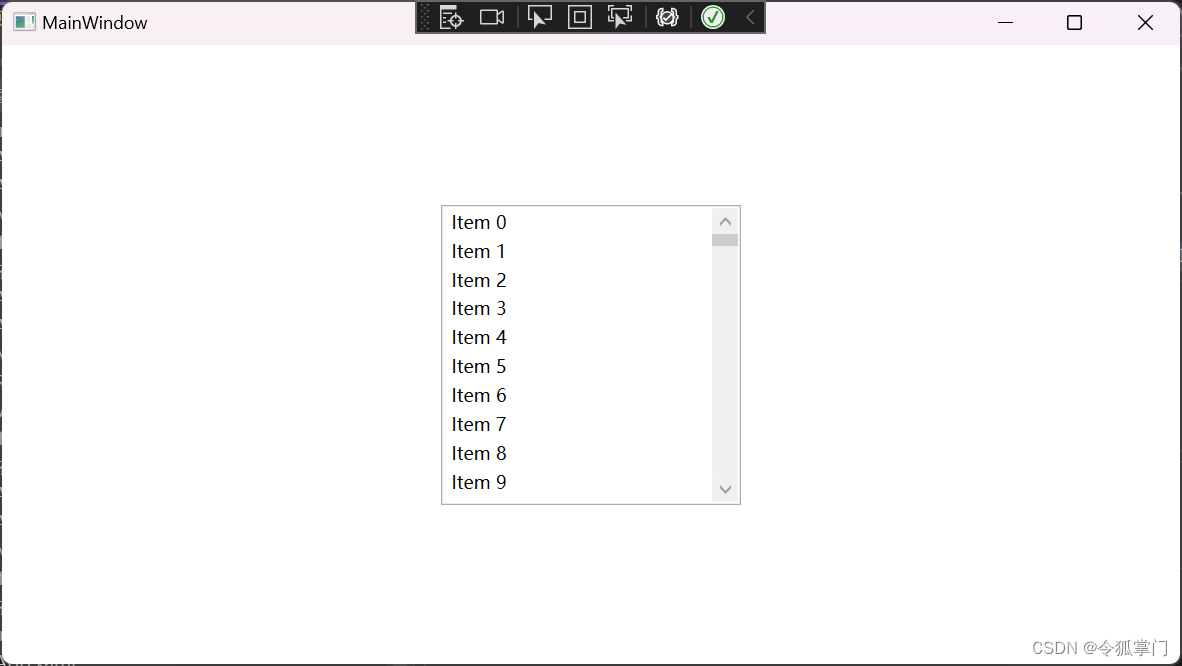
WPF中的虚拟化是什么
WPF(Windows Presentation Foundation)中的虚拟化是一种性能优化技术,它主要用于提高大量数据展示的效率。在WPF中,如果你有一个包含大量项的ItemsControl(例如ListBox、ListView或DataGrid等),…...

免费稳定几乎无门槛,我的ChartGPT助手免费分享给你
公众号「架构成长指南」,专注于生产实践、云原生、分布式系统、大数据技术分享。 概述 ChatGPT想必大家应该都不陌生了,大部分人或多或少都接触了,好多应该都是通过openAi的官方进行使用的,这个门槛对大部分人有点高,…...
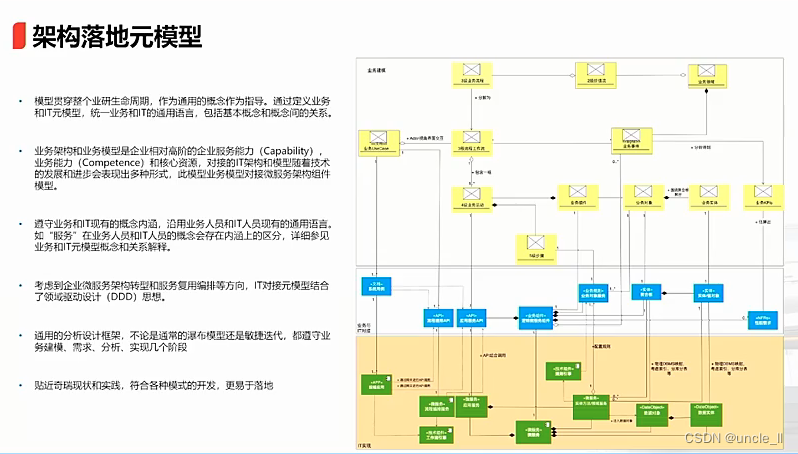
奇瑞金融:汽车金融行业架构设计
拆借联合贷款abs...

milvus数据库分区管理
一、创建分区 在创建集合时,会默认创建分区_default。 自己手动创建如下: from pymilvus import Collection collection Collection("book") # Get an existing collection. collection.create_partition("novel")二、检测分…...

pytorch.nn.Conv1d详解
通读了从论文中找的代码,终于找到这个痛点了! 以下详解nn.Conv1d方法 1 参数说明 in_channels(int) – 输入信号的通道。 out_channels(int) – 卷积产生的通道。 kernel_size(int or tuple) - 卷积核的尺寸,经测试后卷积核的大小应为in_cha…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...
