【开发流程】持续集成、持续交付、持续部署
一、开发工作流程
假设把开发流程分为以下几个阶段:
编码 -> 构建 -> 集成 -> 测试 -> 交付 -> 部署
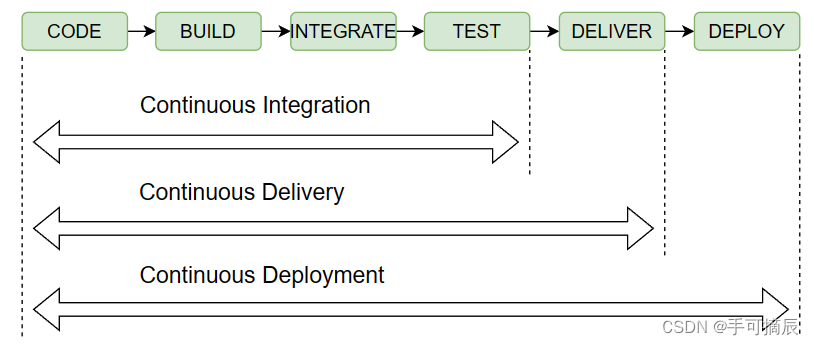
如上图所示,持续集成、持续交付、持续部署有着不同的软件自动交付周期。
二、持续集成、持续交付、持续部署
1、持续集成
持续集成强调开发人员提交了新代码之后,立刻进行构建、(单元)测试。根据测试结果,我们可以确定新代码和原有代码能否正确地集成在一起。
2、持续交付
持续交付在持续集成的基础上,将集成后的代码部署到更贴近真实运行环境的「类生产环境」(production-like environments)中。比如,我们完成单元测试后,可以把代码部署到连接数据库的 Staging 环境中更多的测试。如果代码没有问题,可以继续手动部署到生产环境中。
3、持续部署
持续部署则是在持续交付的基础上,把部署到生产环境的过程自动化。
4、三者关系
将持续集成扩充到部署到生产环境就是持续交付和持续部署的概念,二者的区别即手动与自动的区别。
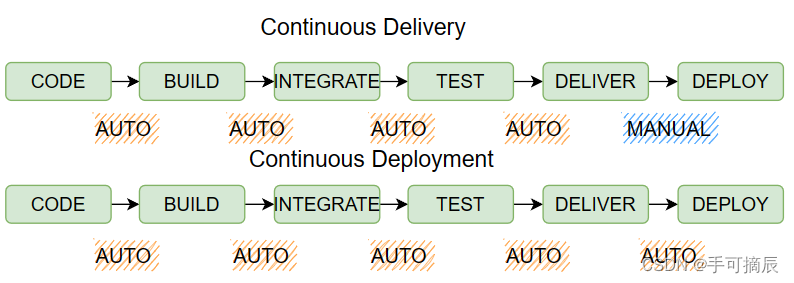
三、持续集成(CI)的价值
1、减少风险
缺陷的检测和修复变得更快,让寻找和修改bug的工作变简单(只修改系统一小部分,无需看太多代码。由于提交后就可以得到反馈,记忆很新鲜,可以进行差异调试)。同时过早的引入集成,使我们能更好的审视各个模块的接口是否满足要求,减少项目中的假定。
2、减少重复过程
由于CI将大量的工作给自动化了,那么可以让人们有时间做更多的需要动脑筋的、更高价值的工作。而且通过对重要过程自动化,克服了项目中某些成员对实现改进的抵制,有利于持续集成的推进。这样就形成了一个良性循环。
在任何时间、任何地点生成可部署的软件
对于客户来说,可以部署的软件是最实际的资产。而CI则可以轻松做到这一点。
3、增强项目的可见性
通过对CI服务器的监控,可以随时了解项目的趋势。CI上的红色或绿色表示了当前项目的健康程度。每一个功能的交付都经历了单元测试或集成测试的考验。
对开发团队的软件产品建立起更强大的产品信心
CI可以防止破窗综合症,让开发团队一点点积累起对产品的信息。
相关文章:

【开发流程】持续集成、持续交付、持续部署
一、开发工作流程 假设把开发流程分为以下几个阶段: 编码 -> 构建 -> 集成 -> 测试 -> 交付 -> 部署 如上图所示,持续集成、持续交付、持续部署有着不同的软件自动交付周期。 二、持续集成、持续交付、持续部署 1、持续集成 持续集成…...

Linux——编译器gcc/g++、调试器gdb以及自动化构建工具makefilemake详解
编译器—gcc/g、调试器—gdb以及自动化构建工具—makefile&&make 文章目录 编译器—gcc/g、调试器—gdb以及自动化构建工具—makefile&&make1. 编译器——gcc/g1.1 生成可执行文件与修改默认可执行文件1.2 程序的翻译过程以及对应的gcc选项1.2.1 预处理 gcc -E…...

Android registerForActivityResults使用详解以及实现原理
registerForActivityResult 使用用途是监听Activity结果。 以下是使用样例 //需要传递Request用于解析Intent和解析上个Activity返回的结果 val launchdata = registerForActivityResult<PickVisualMediaRequest, Uri?>(ActivityResultContracts.PickVisualMedia()) {…...

模拟实现一个Linux中的简单版shell
exec系列接口中的环境变量 在之前我们学习了exec系类函数的功能就是将一个程序替换成另外一个程序。 然后就会出现下面的问题: 首先父进程对应的环境变量的信息是从bash中来的,因为我们自己写的父进程在运行的时候首先就要成为bash的子进程。这里我们将…...
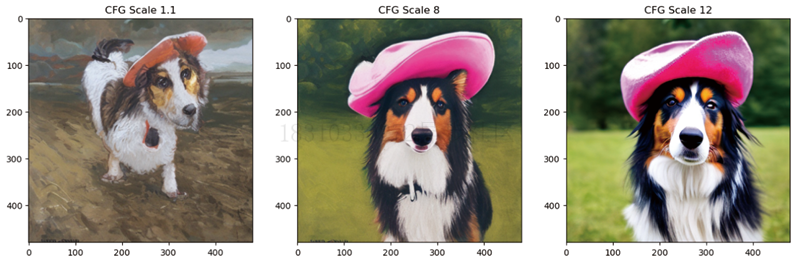
扩散模型实战(十):Stable Diffusion文本条件生成图像大模型
推荐阅读列表: 扩散模型实战(一):基本原理介绍 扩散模型实战(二):扩散模型的发展 扩散模型实战(三):扩散模型的应用 扩散模型实战(四ÿ…...

LaTex编写伪代码,并实现根据所在章编号(连字符),例如算法1-1
1 首先导入包: 按需要添加或者删除option,但是algochapter是必须的。 \usepackage[linesnumbered,ruled,algochapter]{algorithm2e}各个option的作用如下: 您好,这是Bing。我可以帮您解释algorithm2e包中这几个option的意思。&a…...

vue.js javascript js判断是值否为空
检查一个对象(Object)是否为空,即不包含任何元素。Javascript 中的对象就是一个字典,其中包含了一系列的键值对(Key Value Pair)。检查一个对象是否为空,等价于检查对象中有没有键值对。 1、如…...

网页开发如何实现简易页面跳动/跳转,html课堂练习/作业,页面ABC的相互跳转
先建一个文件夹,文件夹包含三个文件夹,三个文件夹分别包含各自的代码。(可以只建一个文件夹,文件夹包含各页面代码) 页面1的代码: <head> <meta http-equiv"Content-Type" content"text/html; charsetu…...

某大型房地产公司绩效面谈项目成功案例纪实
——开展有效的绩效面谈,促进和完善管理工作 【客户行业】房地产行业;国有企业 【问题类型】绩效面谈改进 【客户背景】 某大型房地产公司是某国企集团的省级分公司,集团公司现拥有北京、上海、广州、山东等8大区域公司,现有员…...
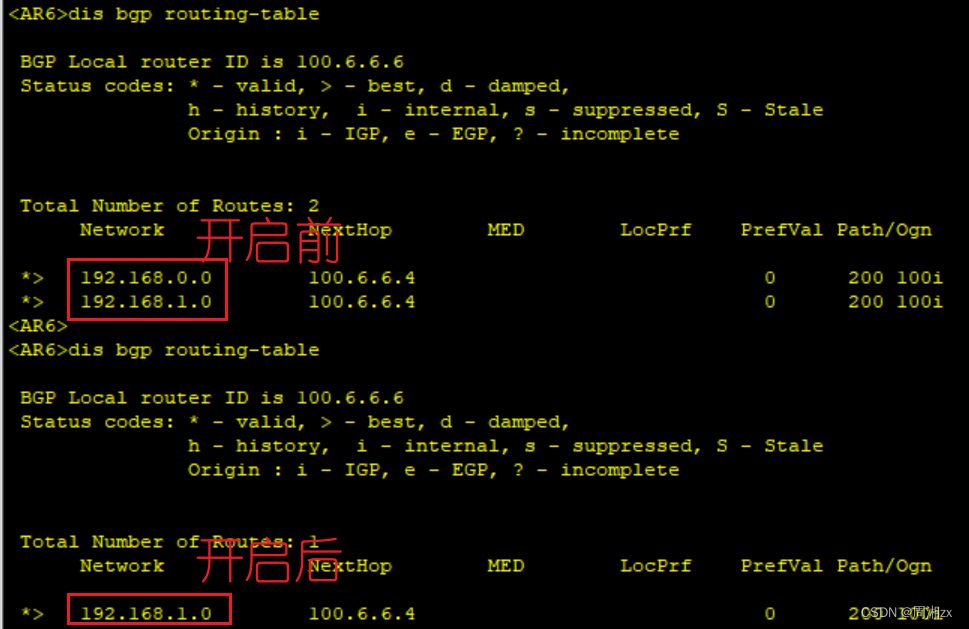
BGP联盟和团体属性实验
目录 一、实验拓扑 二、实验要求 三、实验步骤 1、IP地址配置 2、ospf配置 3、BGP建邻 4、宣告网段 5、配置团体属性 一、实验拓扑 二、实验要求 1、按照图示配 IP 地址,R2,R3,R4,R5分别配 Loopbacke 口地址作为OSPF的Ro…...
代码随想录-刷题第二天
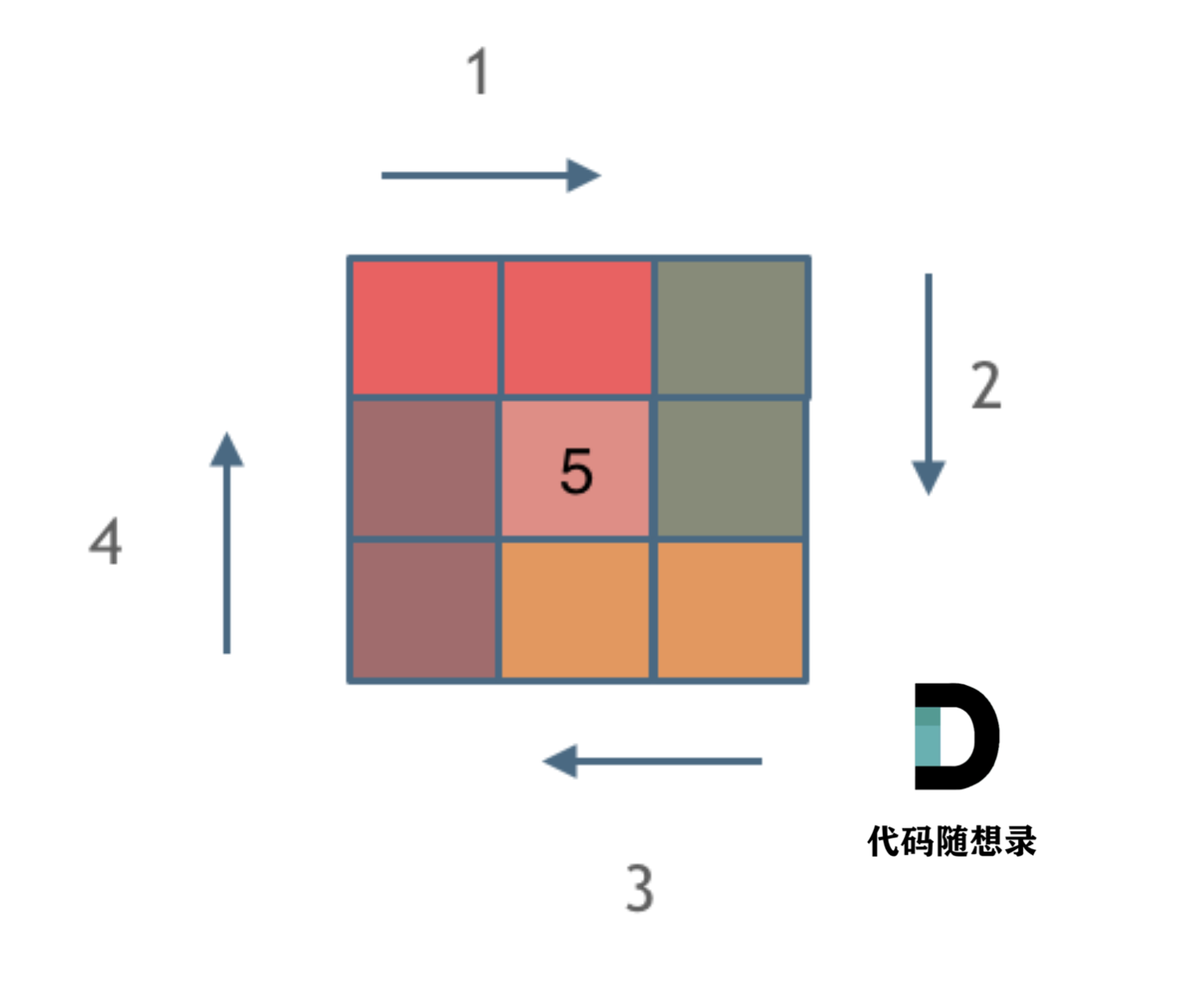
977. 有序数组的平方 题目链接:977. 有序数组的平方 思路:双指针思想,数组是有序的且含有负数,其中元素的平方一定是两边最大。定义两个指针,从两端开始向中间靠近,每次比较两个指针的元素平方大小&#…...
DAY59 503.下一个更大元素II + 42. 接雨水
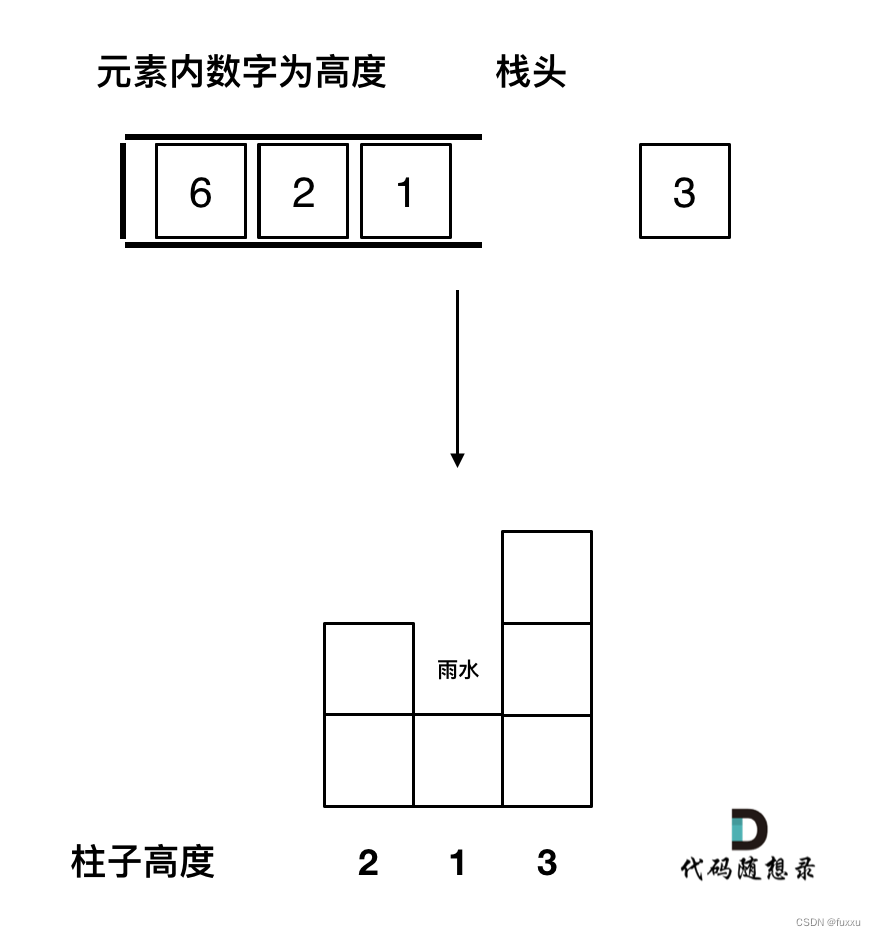
503.下一个更大元素II 题目要求: 给定一个循环数组(最后一个元素的下一个元素是数组的第一个元素),输出每个元素的下一个更大元素。数字 x 的下一个更大的元素是按数组遍历顺序,这个数字之后的第一个比它更大的数&am…...

【如何将任何直流电机变成伺服电机】
【如何将任何直流电机变成伺服电机】 1 前沿2 伺服电机工作原理3 如何制作定制伺服电机4 AS5600 编码器 – 磁性旋转位置传感器5 定制伺服电机电路图6 PCB设计7 自定义伺服3D模型8 定制伺服齿轮箱的 3D 打印零件9 对控制器进行编程9.1 引导加载程序刻录9.2 代码上传9.3 源代码9…...

单片机语音芯片在工业控制中的应用优势
单片机语音芯片,这一智能化的代表产品,不仅在家庭和消费电子领域发挥着重要的作用,更为工业控制领域注入了新的活力。将单片机语音芯片与语音交互技术相结合,为工业设备的控制和监测提供了前所未有的解决方案。 首先,…...

【开源】基于Vue.js的高校实验室管理系统的设计和实现
项目编号: S 015 ,文末获取源码。 \color{red}{项目编号:S015,文末获取源码。} 项目编号:S015,文末获取源码。 目录 一、摘要1.1 项目介绍1.2 项目录屏 二、研究内容2.1 实验室类型模块2.2 实验室模块2.3 实…...

Xrdp+内网穿透实现远程访问Linux Kali桌面
XrdpCpolar实现远程访问Linux Kali桌面 文章目录 XrdpCpolar实现远程访问Linux Kali桌面前言1. Kali 安装Xrdp2. 本地远程Kali桌面3. Kali 安装Cpolar 内网穿透4. 配置公网远程地址5. 公网远程Kali桌面连接6. 固定连接公网地址7. 固定地址连接测试 前言 Kali远程桌面的好处在于…...

【洛谷算法题】P5713-洛谷团队系统【入门2分支结构】
👨💻博客主页:花无缺 欢迎 点赞👍 收藏⭐ 留言📝 加关注✅! 本文由 花无缺 原创 收录于专栏 【洛谷算法题】 文章目录 【洛谷算法题】P5713-洛谷团队系统【入门2分支结构】🌏题目描述🌏输入格…...
Eclipse切换中文环境
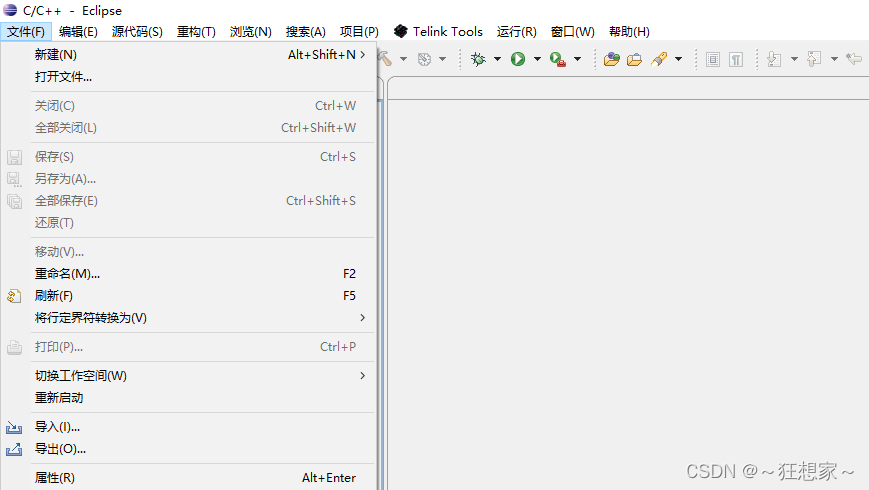
PACK包链接 地址,进入后可以看到不同版本的包。 要选择跟自己Eclipse版本一致的包,比如我的Eclipse启动界面如下,我就要找Helios的包( Juno、Indigo、Helios、Kepler这些具体怎么划分的我也不清楚)。 在线安装 打…...

栈和队列概念
栈stack 栈只能在一端插入/删除元素先入后出只能从栈顶插入,栈顶删除栈底不允许插入和删除push:进栈pop:出栈应用场景: 队列 Queue 队列的插入操作称为 “入队”(Enqueue),是在队尾进行的&am…...
a标签下载文件与解决浏览器默认打开某些格式文件的问题
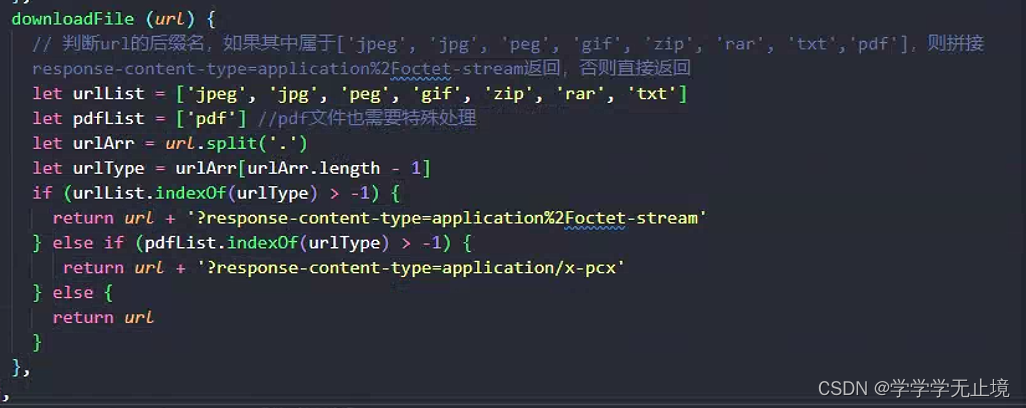
前言 在实际项目中,我们通常会遇到这么一个需求:后端给前端返回一个任意文件类型的完整的url路径,前端拿到这个路径直接通过浏览器下载文件到本地。我想大家应该都会首先想到使用HTML中的<a>标签,,因为<a>…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...

day36-多路IO复用
一、基本概念 (服务器多客户端模型) 定义:单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用:应用程序通常需要处理来自多条事件流中的事件,比如我现在用的电脑,需要同时处理键盘鼠标…...
