数据结构 第八章 查找(静态查找表)
集合
1、集合中的数据元素除了属于同一集合外,没有任何的逻辑关系
2、在集合中,每个数据元素都有一个区别于其他元素的唯一标识(键值或者关键字值)
3、集合的运算:
1 查找某一元素是否存在(内部查找、外部查找)
2 将集合中的元素按照它的唯一标识进行排序
4、集合的存储:
1 任何容器都可以存储集合
2 常用的表示形式是借鉴于线性表或树
5、唯一 一个仅适合于存储和处理集合的数据结构是散列表
注意:
散列表不但是一种存储方法也是一种查找方法
查找
1、查找表:用于查找的集合称为查找表
2、查找表的分类:
1 静态查找表:其中的元素是静态的(不会动态变化)
2 动态查找表:其中的元素经常进行插入和删除操作(会动态变化)
3、平均查找长度:是指查找过程中对关键码的平均比较次数

注意:顺序查找从左到右
顺序查找(无序表)
毫无选择只能做线性的顺序查找

注意:监视哨在data[0]的位置

核心步骤:(一定是可以找到该元素的)
int i;
data[0] = k;
//从后往前查找
for(i=data.size()-1;k!=data[i];--i)
return i;
//查找成功返回该元素的对应下标
//查找失败返回0(在下标为0的位置找到该元素)
顺序查找(有序表)
和无序表的顺序查找是类似的,只是当被查找元素在表中不存在的时候,不需要遍历到表尾
例如:在0 2 4 6 8 中查找5的时候,从后往前遍历,走到4的时候就可以结束遍历

核心步骤:
int i;
data[0] = k;
//从后往前查找
for(i=data.size()-1;k<data[i];--i)
if(k == data[i]) return i;
return 0;
无序表的顺序查找的平均查找长度(ASL)
注意:从后往前进行比较
推导:
1 查找第一个元素需要比较n次
2 查找第二个元素需要比较n-1次
3 ...
4 查找第n个元素需要比较1次
5 那么总共需要比较n*(n+1)/2
6 假设每个关键码都是等概率的:p = 1/n
7 那么n*(n+1)/2 * 1/n = (n+1)/2
8 也就是说:在查找成功的情况下平均需要比较(n+1)/2个元素


注意:n*(n+1)*(1/n) = (n+1)
1 查找每个元素都需要从末尾比较到0
该算法的时间复杂度为O(n)

折半查找(二分查找)


查找成功:

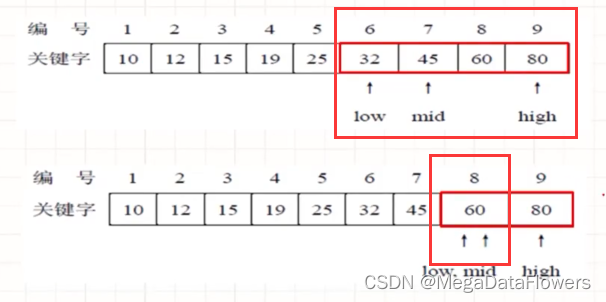
查找失败:


非递归折半查找:

int low = 1;
int high = data.size()-1;
int mid;while(low<=high)
{mid = (low+high)/2;if(k == data[mid]) return mid;if(k<data[mid]) high = mid-1;else low = mid+1;
}return 0;

递归折半查找:

折半查找(判定树)

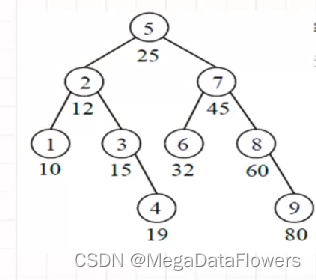
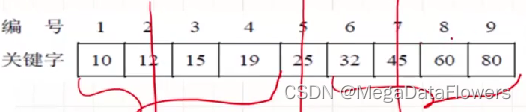
注意:
对判定树进行中序遍历得到的序列和有序表一样
外部结点和内部结点:
注意:
1 外部结点数目 = 内部结点数目 + 1
2 外部结点都是叶子结点
3 内部结点都是度为2的结点
4 n0 = n2 + 1
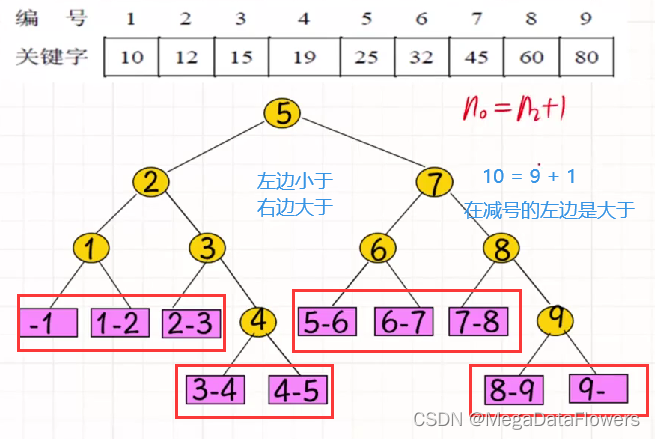
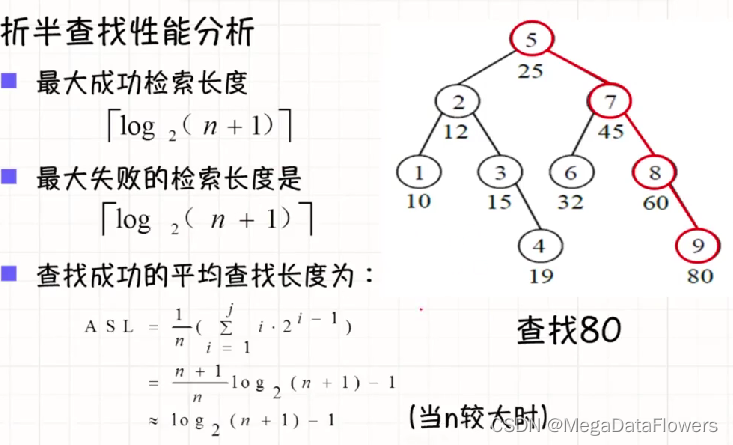
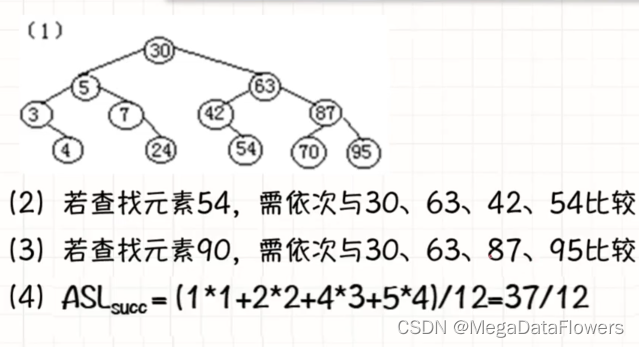
计算平均查找长度:
1 查找成功(内部结点):(1*1+2*2+3*4+4*2)/9 = 25/9
2 查找失败(外部结点):(3*6+4*4)/10 = 34/100

折半查找的性能:

分块查找(索引顺序块的查找)

注意:
1 块之间是有序的(第一块所有值小于第二块的所有值...)
2 在块内的元素之间可能有序也可能无序
索引表:
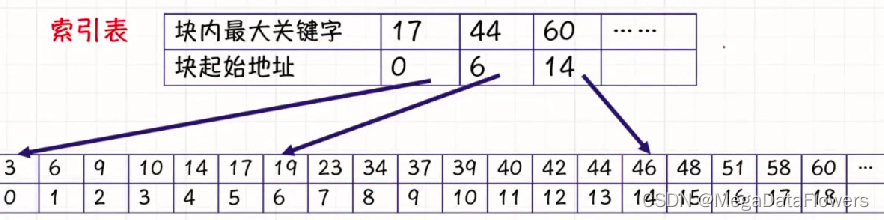

注意:
1 先在索引表内查找
2 在对应块内的查找
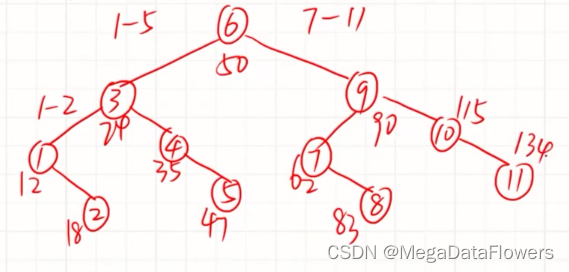
典型题目解析

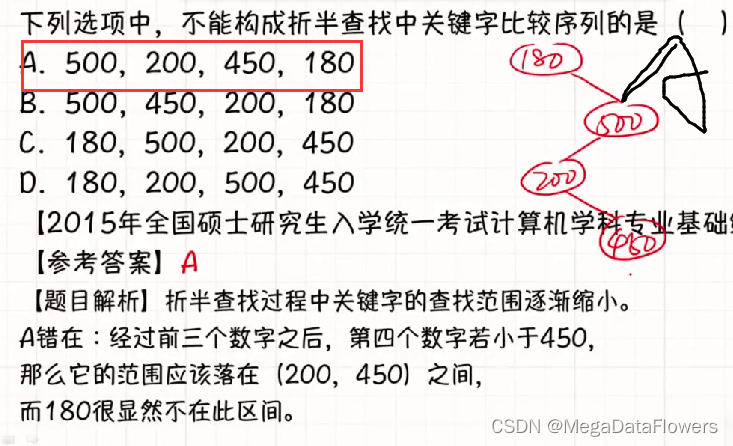
解释:
1 左边是小于
2 右边是大于
3 判断是否为一条直线
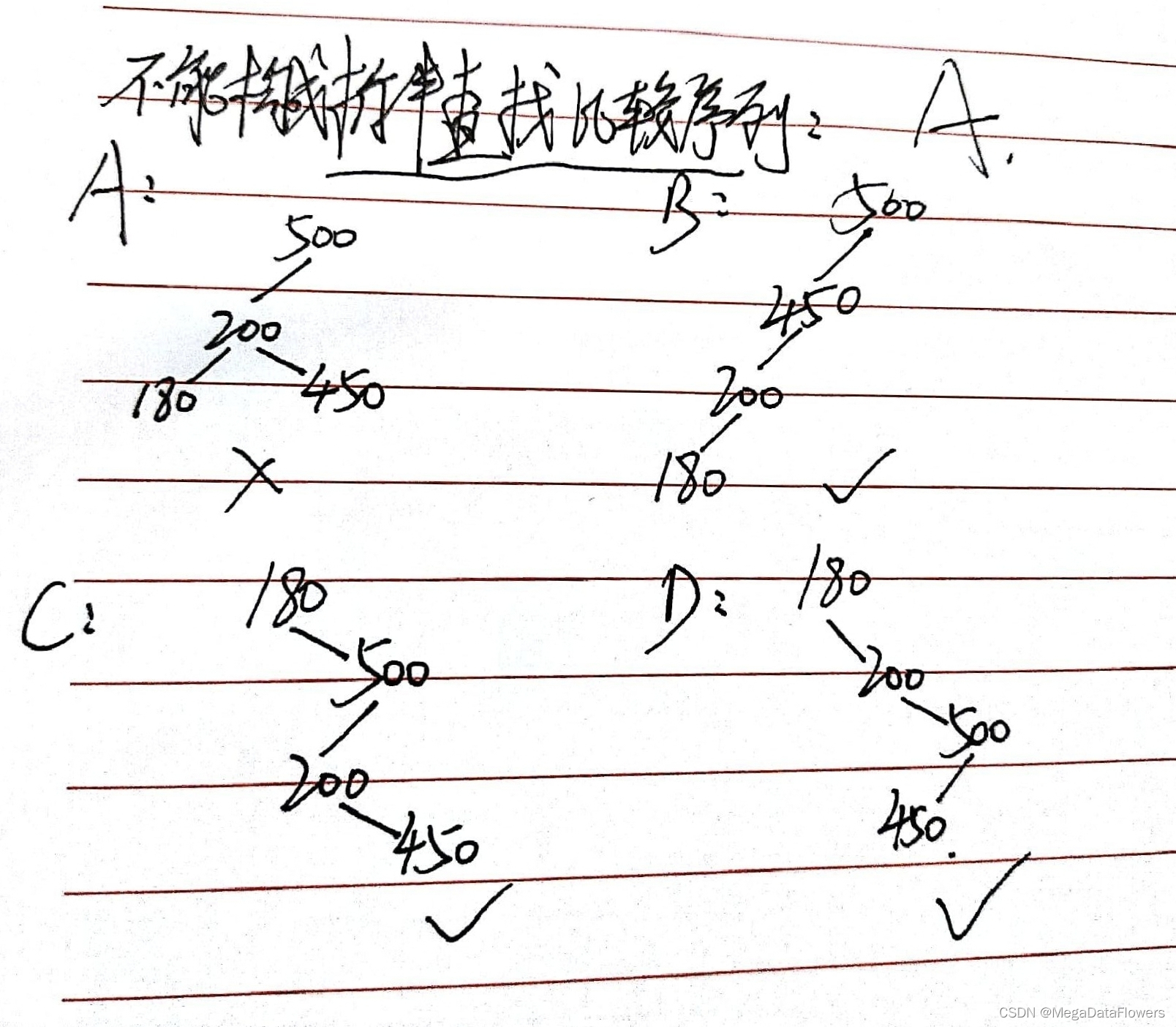

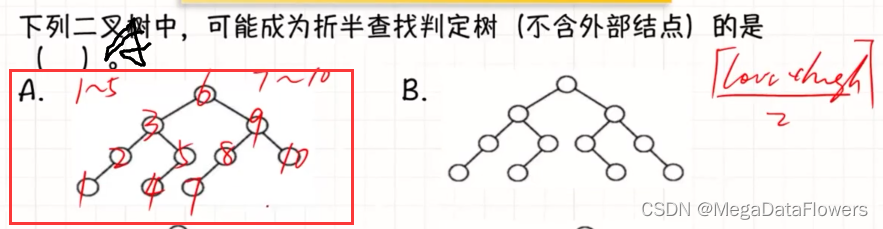

注意:
左分支高度大于等于右分支(向上取整)
易错题

注意:折半查找判定树的高度和完全二叉树的高度是一致的
1 向下取整:**右分支的长度大于等于左分支的长度**
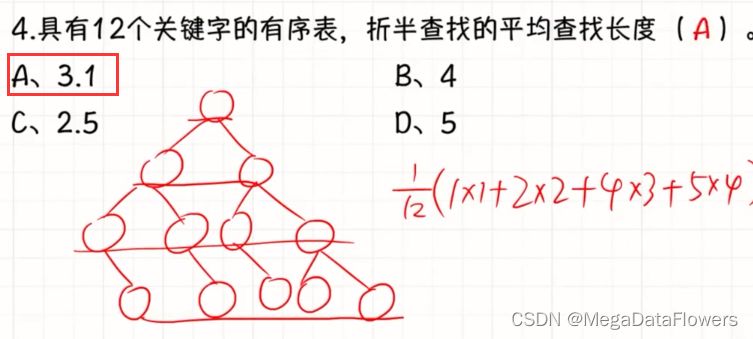



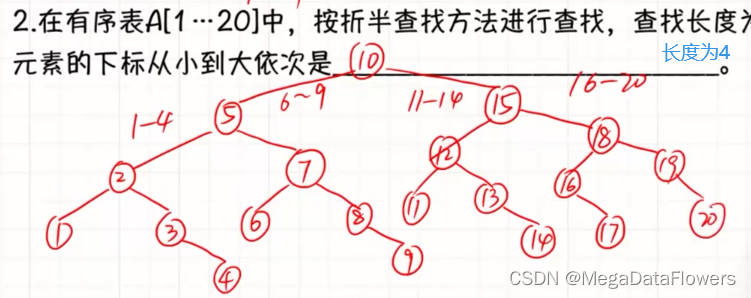

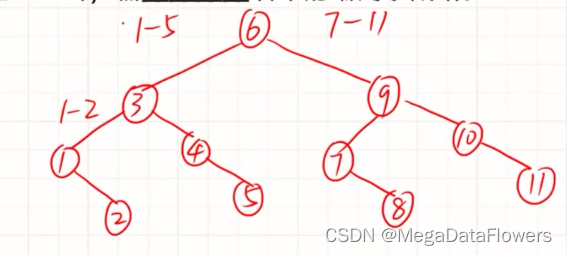
答案为:
1 3 6 8 11 13 16 19





相关文章:

数据结构 第八章 查找(静态查找表)
集合 1、集合中的数据元素除了属于同一集合外,没有任何的逻辑关系 2、在集合中,每个数据元素都有一个区别于其他元素的唯一标识(键值或者关键字值) 3、集合的运算: 1 查找某一元素是否存在(内部查找、外部查找) 2 将集合中的元素按照它的唯一标识进行排序4、集合的…...
)
【Python基础】数据类型(元组、列表)
文章目录二. 数据类型2.1 元组 tuple2.1.1 定义特性2.1.2 拼接拷贝2.1.3 元组拆包2.1.4 元组方法 count2.2 列表 list2.2.1 基础定义2.2.2 增删操作2.2.3 连接联合2.2.4 其他常规操作2.2.5 列表推导式2.2.6 生成器表达式2.x 小结:何时使用元组或列表二. 数据类型 Py…...

你了解互联网APP搜索和推荐的背后逻辑么?
1.搜索和推荐无处不在我们习惯了百度、Google、360搜索的便捷,输入你想要搜索的关键词,立马呈现给你一批对应的结果,供你筛选。我们也经常上淘宝、京东、拼多多购物,输入想买的商品,瞬间列出一页一页的商品清单供我们选…...

Bug的级别,按照什么划分
Bug分类和定级一、bug的定义二、bug的类型三、bug的等级四、bug的优先级一、bug的定义一般是指不满足用户需求的则可以认为是bug,狭义指软件程序的漏洞或缺陷,广义指测试工程师或用户提出的软件可改进的细节、或与需求文档存在差异的功能实现等对应三个测…...
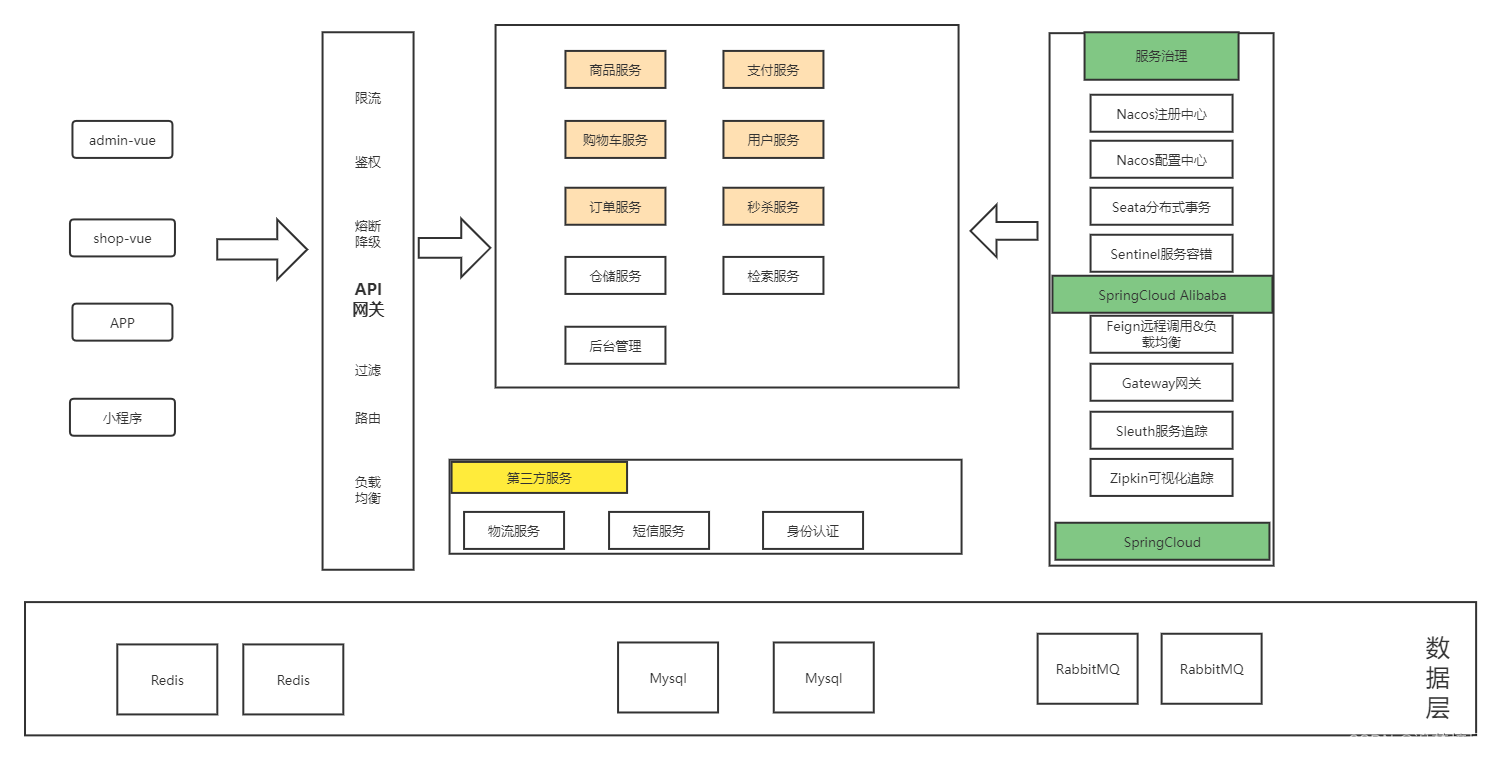
微服务项目简介
项目简介 项目模式 电商模式:市面上有5种常见的电商模式,B2B、B2C、 C2B、 C2C、O2O; 1、B2B模式 B2B (Business to Business),是指 商家与商家建立的商业关系。如:阿里巴巴 2、B2C 模式 B2C (Business to Consumer), 就是我们经常看到的供…...

SLAM中坐标轴旋转及ros的接口解释
读完几个loam算法,满篇的坐标轴旋转,还是手写的(作者,用eigen写不好嘛。。。),我滴天适应了好久…,今天就总结一下坐标轴旋转问题。 一、首先,我们看一下ros中关于欧拉角旋转的函数:setRPY、set…...
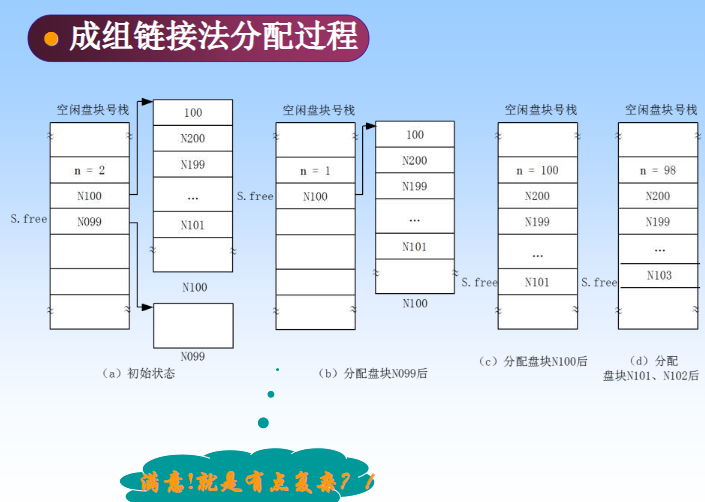
文件管理(9)
文件管理 0 引言 为什么要引入文件系统? 信息管理的需要:用户面前提供一种规格化的机制,方便用户对文件的存取、提高效率。操作系统本身需要–操作系统本身也不是常驻内存的,也有大量的信息需要存于外存。 1 文件定义 文件&a…...

PyTorch学习笔记:nn.TripletMarginLoss——三元组损失
PyTorch学习笔记:nn.TripletMarginLoss——三元组损失 torch.nn.TripletMarginLoss(margin1.0, p2.0, eps1e-06, swapFalse, size_averageNone, reduceNone, reductionmean)功能:创建一个三元组损失函数(triplet loss),用于衡量输入数据x1,x…...

冒泡排序详解
冒泡排序是初学C语言的噩梦,也是数据结构中排序的重要组成部分,本章内容我们一起探讨冒泡排序,从理论到代码实现,一步步深入了解冒泡排序。排序算法作为较简单的算法。它重复地走访过要排序的数列,一次比较两个元素&am…...
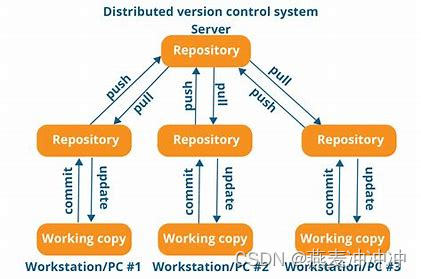
git极快上手指南超级精简版
注:本文参考https://www.liaoxuefeng.com/wiki/896043488029600 原文非常值得一读,作者学识渊博,补充了很多有意思的知识。我仅仅是拾人牙慧。 git是最先进的分布式版本控制系统。 版本控制系统——自动记录系统中文件的改动情况࿰…...
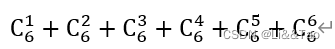
蓝桥杯-最长公共子序列(线性dp)
没有白走的路,每一步都算数🎈🎈🎈 题目描述: 已知有两个数组a,b。已知每个数组的长度。要求求出两个数组的最长公共子序列 序列 1 2 3 4 5 序列 2 3 2 1 4 5 子序列:从其中抽掉某个或多个元素而产生的新…...

GO的并发模式Context
GO的并发模式Context 文章目录GO的并发模式Context一、介绍二、Context三、context的衍生四、示例:Google Web Search4.1 server程序4.2 userip 包4.3 google 包五、使用context包中程序实体实现sync.WaitGroup同样的功能(1)使用sync.WaitGro…...
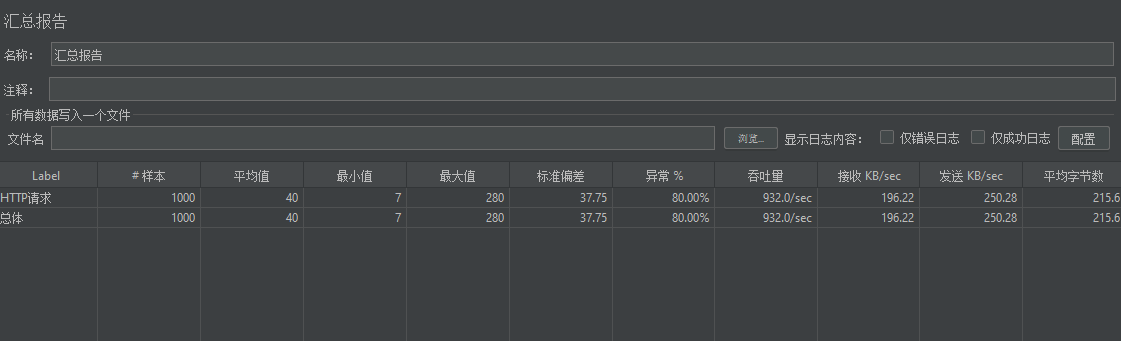
《Redis实战篇》六、秒杀优化
6、秒杀优化 6.0 压力测试 目的:测试1000个用户抢购优惠券时秒杀功能的并发性能~ ①数据库中创建1000用户 这里推荐使用开源工具:https://www.sqlfather.com/ ,导入以下配置即可一键生成模拟数据 {"dbName":"hmdp",…...
)
《C++ Primer Plus》第16章:string类和标准模板库(11)
其他库 C 还提供了其他一些类库,它们比本章讨论前面的例子更为专用。例如,头文件 complex 为复数提供了类模板 complex,包含用于 float、long 和 long double 的具体化。这个类提供了标准的复数运算及能够处理复数的标准函数。C11 新增的头文…...

声明和定义
前言 很多编程语言的语法中都有关于声明和定义的概念,这种概念一般会应用于函数或变量的创建和使用中,但是为什么要这么做? 以C语言为例,一些书籍或教程会要求读者在程序文件开头写上函数和变量的声明,然后再在后面对…...

Python获取最小路径,查找元素在list中的坐标
# codingutf-8__author__ Jeff.xiedef t(li):pass获取最小路径def minPathSum(grid):if not grid:return 0m len(grid) #m列n len(grid[0]) #n行print(grid[0])print("m: ",m)print("n: ",n)#创建一个二维数组dp [[0]*n for _ in range(m)]print(dp) #这…...

数据采集协同架构,集成马扎克、西门子、海德汉、广数、凯恩帝、三菱、海德汉、兄弟、哈斯、宝元、新代、发那科、华中各类数控以及各类PLC数据采集软件
文章目录 前言一、采集协同架构是什么?可以做什么(数控、PLC配置采集)?二、使用步骤 1.打开软件,配置MQTT或者数据库(支持sqlserver、mysql等)存储转发消息规则2.配置数控系统所采集的参数、转…...
Allegro172版本如何用自带的功能实现快速在1MMBGA下方等距放置电容
Allegro172版本如何用自带的功能实现快速在1MMBGA下方等距放置电容 在做PCB设计的时候,在1MM中心间距的BGA背面放置电容,是非常常见的设计,如何快速把电容等距放在BGA下方,除了借助辅助工具外,在Allegro升级到了172版本的时候,可以借助本身自带的功能实现快速放置,以下图…...

一种简单的统计pytorch模型参数量的方法
nelememt()函数Tensor.nelement()->引自Tensor.numel()->引自torch.numel(input)三者的作用是相同的Returns the total number of elements in the inputtensor.返回当前tensor的元素数量利用上面的函数刚好可以统计模型的参数数量parameters()函数Module.parameters(rec…...

【PyTorch】教程:对抗学习实例生成
ADVERSARIAL EXAMPLE GENERATION 研究推动 ML 模型变得更快、更准、更高效。设计和模型的安全性和鲁棒性经常被忽视,尤其是面对那些想愚弄模型故意对抗时。 本教程将提供您对 ML 模型的安全漏洞的认识,并将深入了解对抗性机器学习这一热门话题。在图像…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

WEB3全栈开发——面试专业技能点P7前端与链上集成
一、Next.js技术栈 ✅ 概念介绍 Next.js 是一个基于 React 的 服务端渲染(SSR)与静态网站生成(SSG) 框架,由 Vercel 开发。它简化了构建生产级 React 应用的过程,并内置了很多特性: ✅ 文件系…...

若依登录用户名和密码加密
/*** 获取公钥:前端用来密码加密* return*/GetMapping("/getPublicKey")public RSAUtil.RSAKeyPair getPublicKey() {return RSAUtil.rsaKeyPair();}新建RSAUti.Java package com.ruoyi.common.utils;import org.apache.commons.codec.binary.Base64; im…...

多元隐函数 偏导公式
我们来推导隐函数 z z ( x , y ) z z(x, y) zz(x,y) 的偏导公式,给定一个隐函数关系: F ( x , y , z ( x , y ) ) 0 F(x, y, z(x, y)) 0 F(x,y,z(x,y))0 🧠 目标: 求 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z、 …...
