LeetCode算法题解(动态规划)|LeetCode322. 零钱兑换、LeetCode279. 完全平方数
一、LeetCode322. 零钱兑换
题目链接:322. 零钱兑换
题目描述:
给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。
计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。
你可以认为每种硬币的数量是无限的。
示例 1:
输入:coins =[1, 2, 5], amount =11输出:3解释:11 = 5 + 5 + 1
示例 2:
输入:coins =[2], amount =3输出:-1
示例 3:
输入:coins = [1], amount = 0 输出:0
提示:
1 <= coins.length <= 121 <= coins[i] <= 231 - 10 <= amount <= 104
算法分析:
题目给出硬币的数量无限,所以这是一道完全背包问题。
定义dp数组及下标含义:
dp[j]表示凑成金额为j所需的硬币最少个数。
递推公式:
dp[j]=min(dp[j],dp[j-coins[i]]+1),现有硬币coins[i],那么凑成金额为j所需的最少硬币数可有凑成金额为j-coins[i]所需最少硬币数推出。
初始化:
因为要求的是最少硬币数,所以除dp[0]初始化成0之外,其他所有情况都要初始化成最大值。
遍历顺序:
先遍历不同面额的硬币,在遍历总金额。
打印dp数组进行验证。
代码如下:
class Solution {public int coinChange(int[] coins, int amount) {int[] dp = new int[amount + 1];for(int i = 1; i < amount + 1; i++) dp[i] = Integer.MAX_VALUE;dp[0] = 0;//除了dp[0]其他都初始化成最大值for(int i = 0; i < coins.length; i++) {//遍历每种硬币for(int j = coins[i]; j <= amount; j++) {//遍历总金额if(dp[j - coins[i]] != Integer.MAX_VALUE) {//注意如果dp[j-coins[i]]是个最大int类型整数的话,dp[j-coins[i]]+1会溢出,变成负数,从而影响比较结果,所以只有它不是初始最大值是,才有选择的必要。dp[j] = Math.min(dp[j], dp[j - coins[i]] + 1);}}}return dp[amount] == Integer.MAX_VALUE ? -1 : dp[amount];}
}二、LeetCode279. 完全平方数
题目链接:279. 完全平方数
题目描述:
给你一个整数 n ,返回 和为 n 的完全平方数的最少数量 。
完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,1、4、9 和 16 都是完全平方数,而 3 和 11 不是。
示例 1:
输入:n =12输出:3 解释:12 = 4 + 4 + 4
示例 2:
输入:n =13输出:2 解释:13 = 4 + 9
提示:
1 <= n <= 104
算法分析:
因为每个完全平方数可以无限取,所以这也是一道完全背包问题。
定义dp数组及下标含义:
dp[j]表示组成和为j的完全平方数最少数量。
递推公式:
dp[j]=min(dp[j],dp[j-i*i]+1),现有完全平方数i*i,那么组成j的最少完全平方数数量可有dp[j-i*i]推导而出,也即组成j-i*i的最少完全平方数数量加上现在这个完全平方数(i*i)。
初始化:
因为要求的是完全平方数最少数量,所以除dp[0]初始化成0外,其他所有情况都要初始化成最大值。
遍历顺序:
先遍历小于等于目标和n的每个完全平方数,在遍历总和。
打印dp数组进行验证。
代码如下:
class Solution {public int numSquares(int n) {int[] dp = new int[n + 1];//除dp[0]意外,其他所有情况都初始化成最大值dp[0] = 0;for(int i = 1; i <= n; i++)dp[i] = Integer.MAX_VALUE;for(int i = 1; i * i <= n; i++) {//遍历每个完全平方数for(int j = i * i; j <= n; j++) {//遍历总和dp[j] = Math.min(dp[j],dp[j-i * i] + 1);}}return dp[n];}
}总结
这两道题都是完全背包问题中,求最少元素个数的情况。
相关文章:
|LeetCode322. 零钱兑换、LeetCode279. 完全平方数)
LeetCode算法题解(动态规划)|LeetCode322. 零钱兑换、LeetCode279. 完全平方数
一、LeetCode322. 零钱兑换 题目链接:322. 零钱兑换 题目描述: 给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。 计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一…...

Python Web开发基础知识篇
一,基础知识篇 本片文章会简单地说一些python开发web中所必须的一些基础知识。主要包括HTML和css基础、JavaScript基础、网络编程基础、MySQL数据库基础、Web框架基础等知识。 1,Web简介 Web,全称为World Wide Web,也就是WWW,万…...

企业计算机服务器中了360勒索病毒怎么办,360勒索病毒解密文件恢复
计算机技术的不断发展,为企业的生产运营提供了极大便利,不仅提升了办公效率,还促进了企业的发展。企业计算机在日常工作中一定加以防护,减少网络威胁事件的产生,确保企业的生产生产运营。最近,网络上的360后…...

LeetCode无重复字符的最长字符串的Java实现
题目 给定一个字符串 s ,请你找出其中不含有重复字符的 最长连续子字符串 的长度。 示例 1: 输入: s "abcabcbb" 输出: 3 解释: 因为无重复字符的最长子字符串是 "abc",所以其长度为 3。示例 2: 输入: s "bbbbb" 输…...
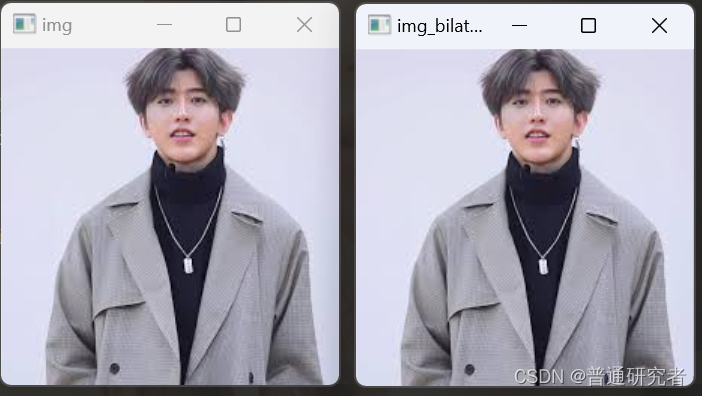
opencv-图像平滑
高斯平滑 高斯平滑即采用高斯卷积核对图像矩阵进行卷积操作。高斯卷积核是一个近似服从高斯分布的矩阵,随着距离中心点的距离增加,其值变小。这样进行平滑处理时,图像矩阵中锚点处像素值权重大,边缘处像素值权重小。 import cv2 …...

【开源】基于Vue.js的天然气工程运维系统的设计和实现
项目编号: S 022 ,文末获取源码。 \color{red}{项目编号:S022,文末获取源码。} 项目编号:S022,文末获取源码。 目录 一、摘要1.1 项目介绍1.2 项目录屏 二、功能模块2.1 系统角色分类2.2 核心功能2.2.1 流程…...
数据丢失抢救神器之TOP10 Android 数据恢复榜单
在快节奏的数字时代,我们的生活越来越与智能手机交织在一起,使它们成为重要数据和珍贵记忆的存储库。由于意外删除、软件故障或硬件故障而丢失数据可能是一种痛苦的经历。值得庆幸的是,技术领域提供了 Android 数据恢复软件形式的解决方案。这…...

梨花声音教育,动作电影中配音也能带来听见“冲击力”
在为动作电影提供配音服务时,配音员家需要通过声音的力量来增强画面上的动作张力、传递角色的活力,以及呈现出电影中的紧迫感。动作片充斥着快节奏的场景交替、紧张的格斗和惊险的逃逸等元素,配音需要精确、生动且充满动力。为动作电影配音应…...

Elaticsearch学习
Elaticsearch 索引 1、索引创建 PUT /index_v1 {"settings": {"number_of_shards": 3,"number_of_replicas": 1},"mappings": {"properties": {"aaa": {"type": "keyword","store&qu…...

【腾讯云云上实验室】向量数据库+LangChain+LLM搭建智慧辅导系统实践
目录 一、搭建智慧辅导系统——向量数据库实践指南1.1、创建向量数据库并新建集合1.2、使用 TKE 快速部署 ChatGLM1.3、部署 LangChain PyPDFVectorDB等组件1.4、配置知识库语料1.5、基于 VectorDB LLM 的智能辅导助手 二、LLM时代的次世代引擎——向量数据库2.1、向量数据库L…...

从0开始学习JavaScript--深入了解JavaScript框架
JavaScript框架在现代Web开发中扮演着关键角色,为开发者提供了丰富的工具和抽象层,使得构建复杂的、高性能的Web应用变得更加容易。本文将深入探讨JavaScript框架的核心概念、常见框架的特点以及它们在实际应用中的使用。 JavaScript框架的作用 JavaSc…...

【教3妹学编程-算法题】二叉树中的伪回文路径
3妹:好冷啊, 冻得瑟瑟发抖啦 2哥 : 又一波寒潮来袭, 外面风吹的呼呼的。 3妹:今天还有雨,2哥上班记得带伞。 2哥 : 好的 3妹:哼,不喜欢冬天,也不喜欢下雨天,要是我会咒语…...
快速上手Banana Pi BPI-M4 Zero 全志科技H618开源硬件开发开发板
Linux[编辑] 准备[编辑] 1. Linux镜像支持SD卡或EMMC启动,并且会优先从SD卡启动。 2. 建议使用A1级卡,至少8GB。 3. 如果您想从 SD 卡启动,请确保可启动 EMMC 已格式化。 4. 如果您想从 EMMC 启动并使用 Sdcard 作为存储,请确…...
Node.js入门指南(三)
目录 Node.js 模块化 介绍 模块暴露数据 导入模块 导入模块的基本流程 CommonJS 规范 包管理工具 介绍 npm cnpm yarn nvm的使用 我们上一篇文章介绍了Node.js中的http模块,这篇文章主要介绍Node.js的模块化,包管理工具以及nvm的使用。 Node…...

Leetcode—2824.统计和小于目标的下标对数目【简单】
2023每日刷题(三十九) Leetcode—2824.统计和小于目标的下标对数目 实现代码 class Solution { public:int countPairs(vector<int>& nums, int target) {int n nums.size();sort(nums.begin(), nums.end());int left 0, right left 1;i…...

【基础架构】part-2 可扩展性
文章目录 可扩展性(Scalability)2.1 水平扩展2.2 垂直扩展2.3 弹性扩展 三、可靠性(Reliability)3.1 容错机制3.2 错误处理和恢复策略3.3 监控和自动化运维 四、 安全性(Security)4.1 身份验证和授权4.2 加…...

[SWPUCTF 2021 新生赛]no_wakeup
直接赋值即可 $a ->admin admin; $a ->passwd wllm; 发现没有绕过,改成大于2的绕过__wakeup 这是因为PHP在反序列化时会检查序列化字符串的长度,如果长度小于等于2,则不会调用__wakeup()方法。...
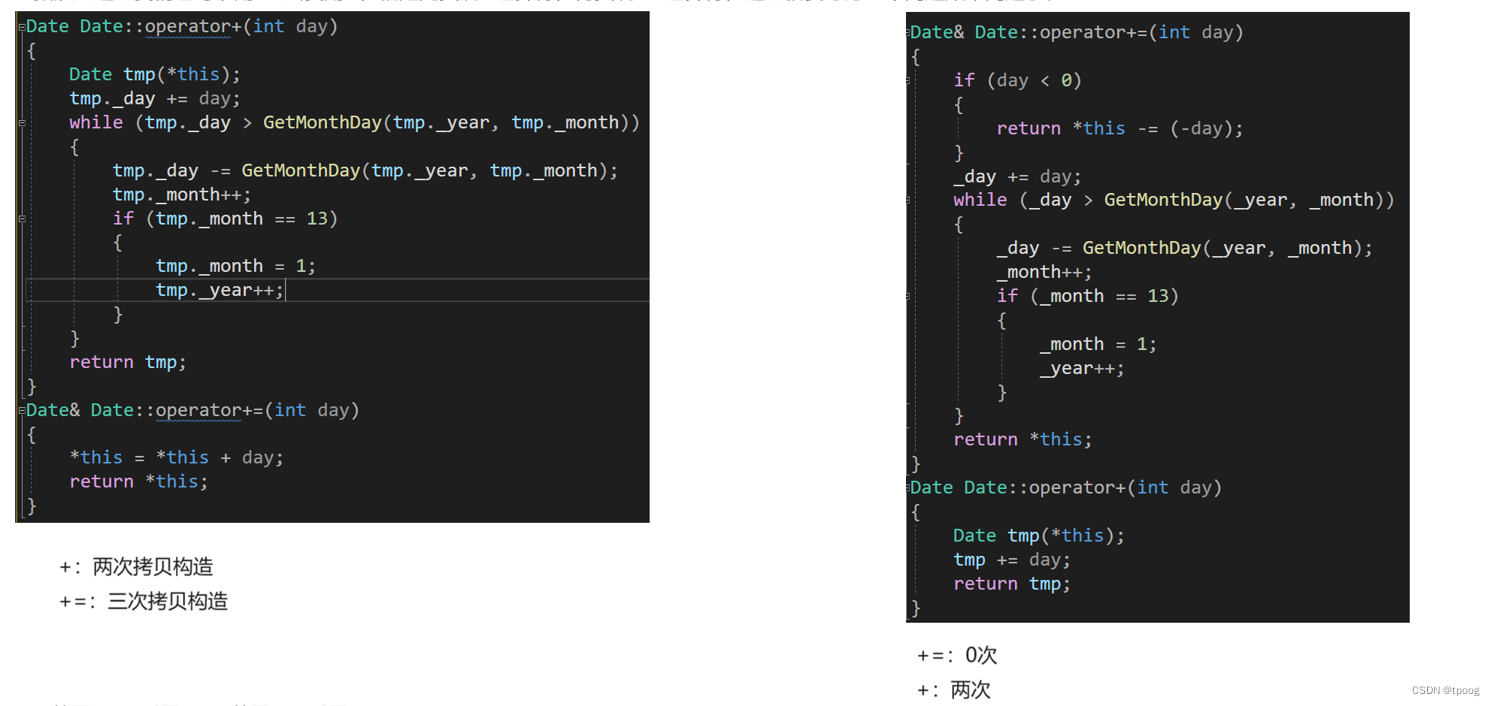
类和对象(3)日期类的实现
日期类的实现 一,声明二,函数成员定义2.1构造函数2.2获取月份天数2.3比较运算符2.3.1等于和大于2.3.2其他 2.4计算运算符2.4.1 &&2.4.2-&&- 2.5日期-日期 一,声明 class Date { public:Date(int year 1, int month 1, int…...

分布式篇---第五篇
系列文章目录 文章目录 系列文章目录前言一、你知道哪些限流算法?二、说说什么是计数器(固定窗口)算法三、说说什么是滑动窗口算法前言 前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。点击跳转到网站,这篇文章男女通用,看懂了就去…...
)
SpringMVC(二)
八、HttpMessageConverter HttpMessageConverter,报文信息转换器,将请求报文转换为Java对象,或将Java对象转换为响应报文 HttpMessageConverter提供了两个注解和两个类型:RequestBody,ResponseBody,Reque…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

华为OD机考-机房布局
import java.util.*;public class DemoTest5 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseSystem.out.println(solve(in.nextLine()));}}priv…...

Kubernetes 网络模型深度解析:Pod IP 与 Service 的负载均衡机制,Service到底是什么?
Pod IP 的本质与特性 Pod IP 的定位 纯端点地址:Pod IP 是分配给 Pod 网络命名空间的真实 IP 地址(如 10.244.1.2)无特殊名称:在 Kubernetes 中,它通常被称为 “Pod IP” 或 “容器 IP”生命周期:与 Pod …...
