力扣:单调栈算法思路题
单调栈分为单调递增栈和单调递减栈,通过使用单调栈我们可以访问到最近一个比它大(小)的元素。
🍊 单调递增栈:单调递增栈就是从栈底到栈顶数据是依次递增,通常是寻找某方向第一个比它小的元素。
🍊 单调递减栈:单调递减栈就是从栈底到栈顶数据是依次递减,通常是寻找某方向第一个比它大的元素。
适用场景
🍋什么情况适合用单调栈来解决实际问题呢?
🍒 通常是在数组中需要通过比较前后元素的大小关系来找最近的比它大(小)的元素问题时,可以使用单调栈进行求解。
场景示例
1:寻找左边第一个小于它的数
/*** 寻找左边第一个小于它的数* 单调递增栈:单调递增栈就是从栈底到栈顶数据是依次递增,通常是寻找某方向第一个比它小的元素* 单调递减栈:单调递减栈就是从栈底到栈顶数据是依次递减,通常是寻找某方向第一个比它大的元素** 题目描述: 给定一个长度为 n ≤ 10 ^5 的数组 a,输出每个数左边第一个比它小的数,如果不存在则输出 − 1。** 在指针 i 从左往右遍历的过程中,我们可以用一个栈来保存 i 左边的所有元素(不包括i指向的元素)* ,下标越大的元素越接近栈顶,下标越小的元素越接近栈底。* 每次我们访问栈顶,只要栈顶元素大于等于 a [ i ],我们就将栈顶元素弹出,直至栈顶元素小于 a [ i ] ,* 此时输出栈顶元素并将 a [ i ] 压入栈中。 由于栈中保存了 i 左边的所有元素,所以只要有答案,则答案一定在栈中。* 由于每个元素一定会被压入一次且至多弹出一次,因此操作次数至多是2n,故总时间复杂度为O(n)* @param array* @return*/public static int[] findFirstLeftLower(int[] array){Deque<Integer> linkList = new LinkedList<>();int[] ans = new int[array.length];for (int i = 0; i < array.length; i++) {// 如果栈不为空且当前数小于等于栈顶元素,则将栈顶出栈,并通过linkList.push(array[i])将当前元素入栈while(!linkList.isEmpty() && array[i] <= linkList.peek()){// 如果是求右边第一个大于它的数,只需要替换成 array[i] >= linkList.peek()linkList.poll();}if(!linkList.isEmpty()){// 由于栈顶元素存放第一个比当前元素小的数,则取出并给结果数组赋值ans[i] = linkList.peek();}else{ans[i] = -1;}linkList.push(array[i]);}/* for (int i = 0; i < ans.length; i++) {System.out.print(ans[i]+" ");}*/return ans;}
2:寻找左边第一个小于它的数的下标
/*** 寻找左边第一个小于它的数的下标* 单调递增栈:单调递增栈就是从栈底到栈顶数据是依次递增,通常是寻找某方向第一个比它小的元素* 单调递减栈:单调递减栈就是从栈底到栈顶数据是依次递减,通常是寻找某方向第一个比它大的元素** 题目描述: 给定一个长度为 n ≤ 10 ^5 的数组 a,输出每个数左边第一个比它小的数的下标,如果不存在则输出 − 1。* 我们只需要注意几个点,在当前条件下,咱们栈中存的是下标,而不是值,* 所以需要修改两个地方:* a[linkList.peek()] 而不是linkList.peek(),* 不再是a[i],而是存储对应的下标i* @param array* @return*/public static int[] findFirstLeftLowerPosition(int[] array){Deque<Integer> linkList = new LinkedList<>();int[] ans = new int[array.length];for (int i = 0; i < array.length; i++) {// 如果栈不为空且当前数小于等于栈顶元素,则将栈顶出栈,并通过linkList.push(array[i])将当前元素入栈while(!linkList.isEmpty() && array[i] <= array[linkList.peek()]){// 如果是求右边第一个大于它的数的下标,只需要替换成 array[i] >= linkList.peek()linkList.poll();}if(!linkList.isEmpty()){// 由于栈顶元素存放第一个比当前元素小的数 对应下标,则取出并给结果数组赋值ans[i] = linkList.peek();}else{ans[i] = -1;}linkList.push(i);}/*for (int i = 0; i < ans.length; i++) {System.out.print(ans[i]+" ");}*/return ans;}
3:LeetCode 42. 接雨水
/*** LeetCode 42. 接雨水* 给定n个非负整数表示每个宽度为1的柱子的高度图,计算按此排序的柱子,下雨后能接多少雨水。* @param height* @return*/public static int trapWater(int[] height) {Deque<Integer> linkList = new LinkedList<>();// 总雨水量int ans = 0;int n = height.length;for (int i = 0; i <n ; i++) {// 当前柱子作为右柱子,栈顶元素作为中间柱,中间柱子前面作为左柱,只能接左右两柱最低柱子高度的水while(!linkList.isEmpty() && height[linkList.peek()] <= height[i]){// 右柱比栈顶更高,才能接水。否则的话,就是满足单调递减栈的,那么我们继续入栈。int top = linkList.pop();// 拿出前一个柱子if(linkList.isEmpty()){// 如果这根柱子后,前面没有元素,那就接不了雨水了,因为接雨水的话,至少需要左右两边都有柱子才行。break;}// 记录一下拿到的这根柱子的左边那根柱子的高度int left = linkList.peek();// 根据柱状图推算宽度int currWidth = i-left-1;int currHeight = Math.min(height[left],height[i]) - height[top];ans += currHeight*currWidth;}linkList.push(i);//经过上面一顿操作之后,咱们的栈又满足单调性了,于是将当前元素的下标入栈。}return ans;}
参考资料
单调栈图文详解
相关文章:

力扣:单调栈算法思路题
单调栈分为单调递增栈和单调递减栈,通过使用单调栈我们可以访问到最近一个比它大(小)的元素。 🍊 单调递增栈:单调递增栈就是从栈底到栈顶数据是依次递增,通常是寻找某方向第一个比它小的元素。 …...
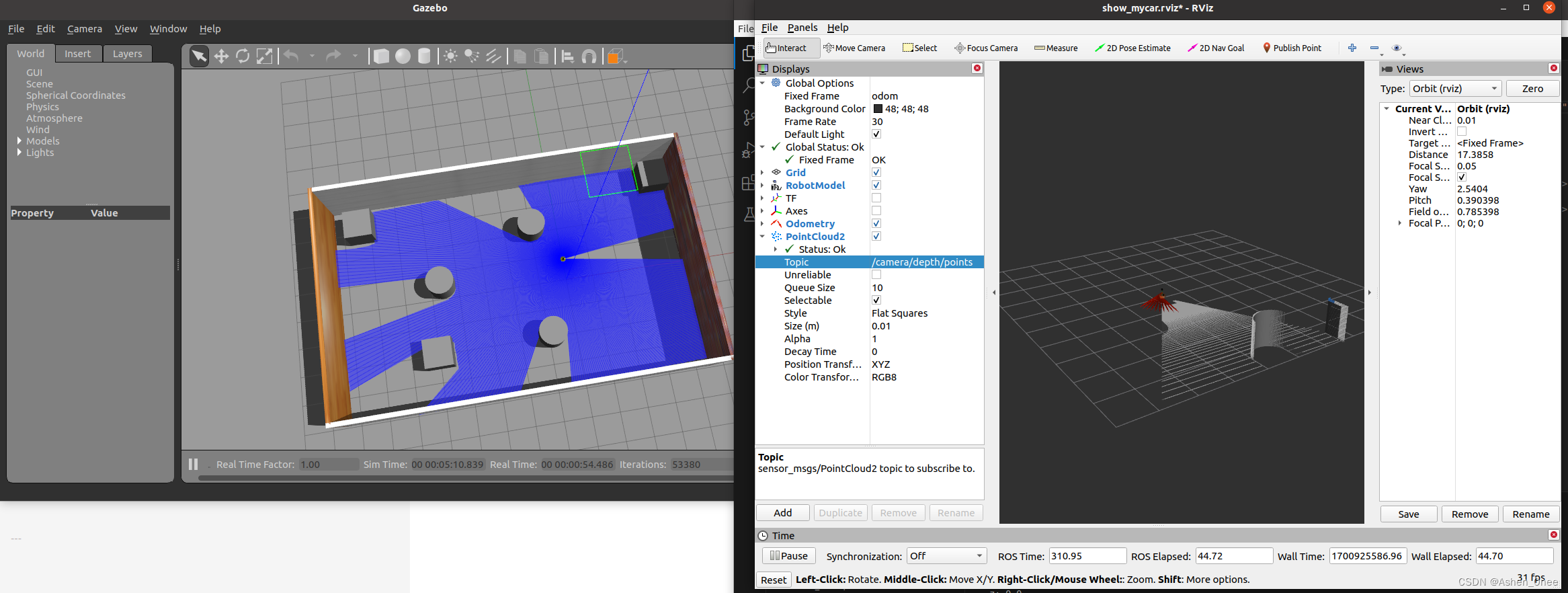
11 月 25 日 ROS 学习笔记——3D 建模与仿真
文章目录 前言一、在 ROS 中自定义机器人的3D模型1. 在 rviz 里查看3D模型2. xacro 二、Gazebo1. urdf 集成 gazebo2. 综合应用1). 运动控制及里程计2). 雷达仿真3). 摄像头信息仿真4). kinect 深度相机仿真5). 点云 前言 本文为11 月 25 日 ROS 学习笔记——3D 建模与仿真&am…...
MidJourney笔记(3)-Prompts
MidJourney的Prompts介绍 MidJourney的Prompts是MidJourney的核心之一,这也是我们后续使用MidJourney过程中最重要的工作内容,根据生成的图片,不断的优化我们的Prompts内容。 那Prompts的中文意思是提示的意思。 Prompts的提示语有很多,最基础的用法就是: /imagine prompt…...

贪心 D. Least Cost Bracket Sequence
Problem - D - Codeforces 题目大意:给一个只包含(,),?三个字符的字符串。每个?可以转为(或者),对于第 i i i个?转为(需要花费 a i a_i ai,转为)需要花费 b i b_i bi。现在问能否让该字符串转为合法的括号匹配…...
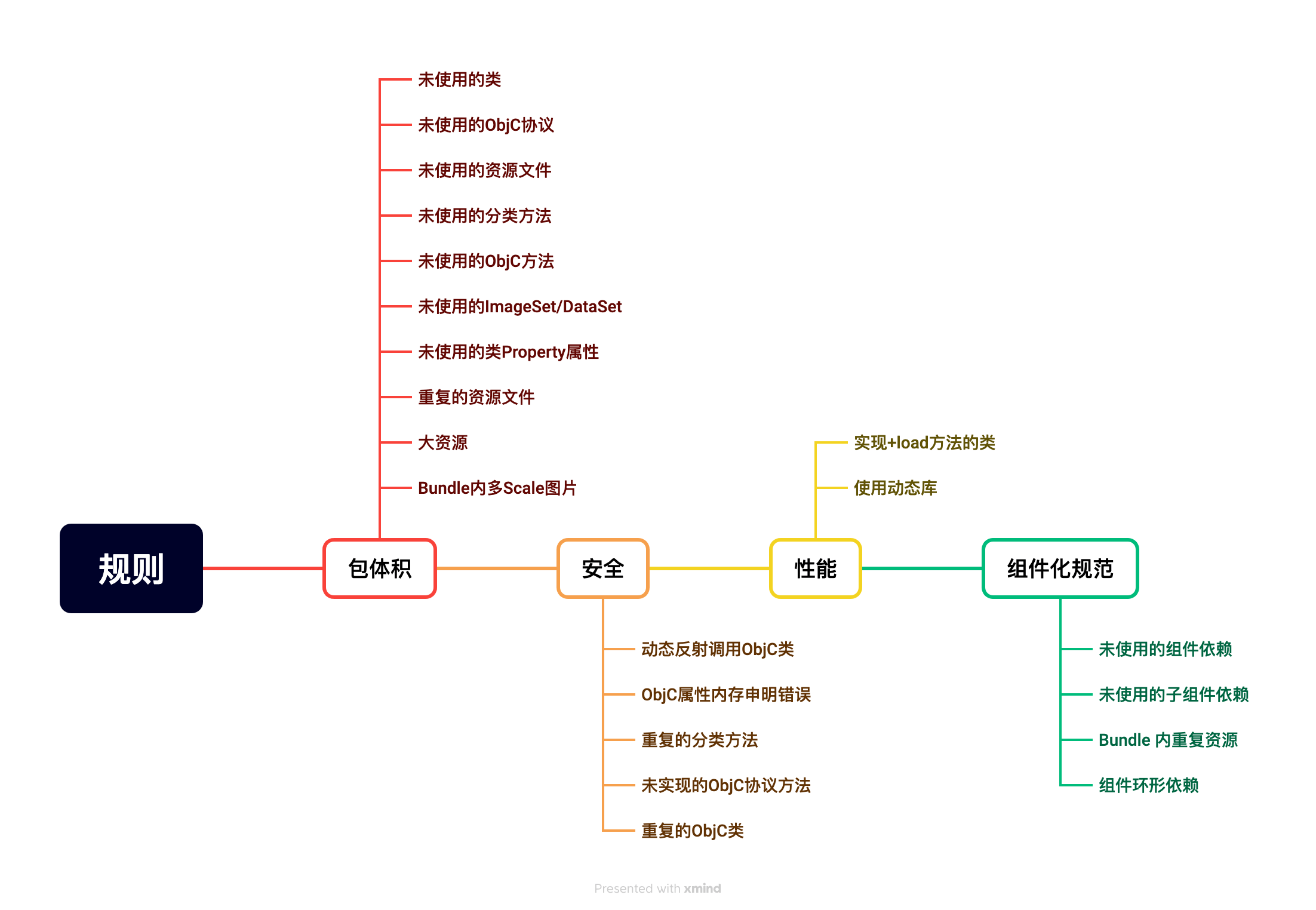
iOS APP包分析工具 | 京东云技术团队
介绍 分享一款用于分析iOSipa包的脚本工具,使用此工具可以自动扫描发现可修复的包体积问题,同时可以生成包体积数据用于查看。这块工具我们团队内部已经使用很长一段时间,希望可以帮助到更多的开发同学更加效率的优化包体积问题。 工具下载…...
在 VSCode 中使用 GDB 进行 C/C++ 程序调试(图文版)
(꒪ꇴ꒪ ),Hello我是祐言QAQ我的博客主页:C/C语言,数据结构,Linux基础,ARM开发板,网络编程等领域UP🌍快上🚘,一起学习,让我们成为一个强大的攻城狮࿰…...

任意文件读取漏洞理解
任意文件读取漏洞理解 1. 漏洞描述: 任意文件读取漏洞是指攻击者可以利用漏洞读取系统上的任意文件,包括敏感信息的配置文件、用户数据甚至系统文件,从而获取未经授权的访问权限。 2. 漏洞原理: 这种漏洞通常是由程序处理用户输入…...

linux 安装yum
问题1:File "/usr/libexec/urlgrabber-ext-down", line 28 except OSError, e: ^ 问题2:yum File "/usr/bin/yum", line 30 except KeyboardInterrupt, e: ^ vim /usr/…...

数学启发式
学习资料: 优化求解器 | Gurobi 数学启发式算法:参数类型与案例实现 数学启发式算法 | 可行性泵 (Feasibility Pump)算法精讲:一份让您满意的【理论介绍编程实现数值实验】学习笔记(PythonGurobi实现) 大佬到底是大佬!这些资料太…...

Win10/Win11 使用Wsl的Ubuntu 子系统搭建CGO环境,相当于Ubuntu下开发。GO环境CGO搭建,支持交叉编译
背景: 之前是使用Mac 开发,最近切换到win11下面。发现使用cgo编译有问题。 下面记载了我的使用方法。 环境: win11(win10理论一样) win11 安装了wsl2的环境,并且安装了ubuntu系统。 在win11 上面安装了g…...

CSS新特性(2-2)
CSS新特性(2-2) 前言box相关box-shadow background背景rgba颜色与透明度transform:rotate(Xdeg) 2D旋转transform:tranlate 平移 前言 本文继续讲解CSS3其他的新特性,想看之前新特性点击这里,那么好本文正式开始。 box相关 box…...
为什么,word文件在只读模式下,仍然能编辑?
Word文档设置了只读模式,是可以编辑的,但是当我们进行保存的时候就会发现,word提示需要重命名并选择新路径才能够保存。 这种操作,即使可以编辑文字,但是原文件是不会受到影响的,编辑之后的word文件会保存到…...

29 - 装饰器模式:如何优化电商系统中复杂的商品价格策略?
开始今天的学习之前,我想先请你思考一个问题。假设现在有这样一个需求,让你设计一个装修功能,用户可以动态选择不同的装修功能来装饰自己的房子。例如,水电装修、天花板以及粉刷墙等属于基本功能,而设计窗帘装饰窗户、…...
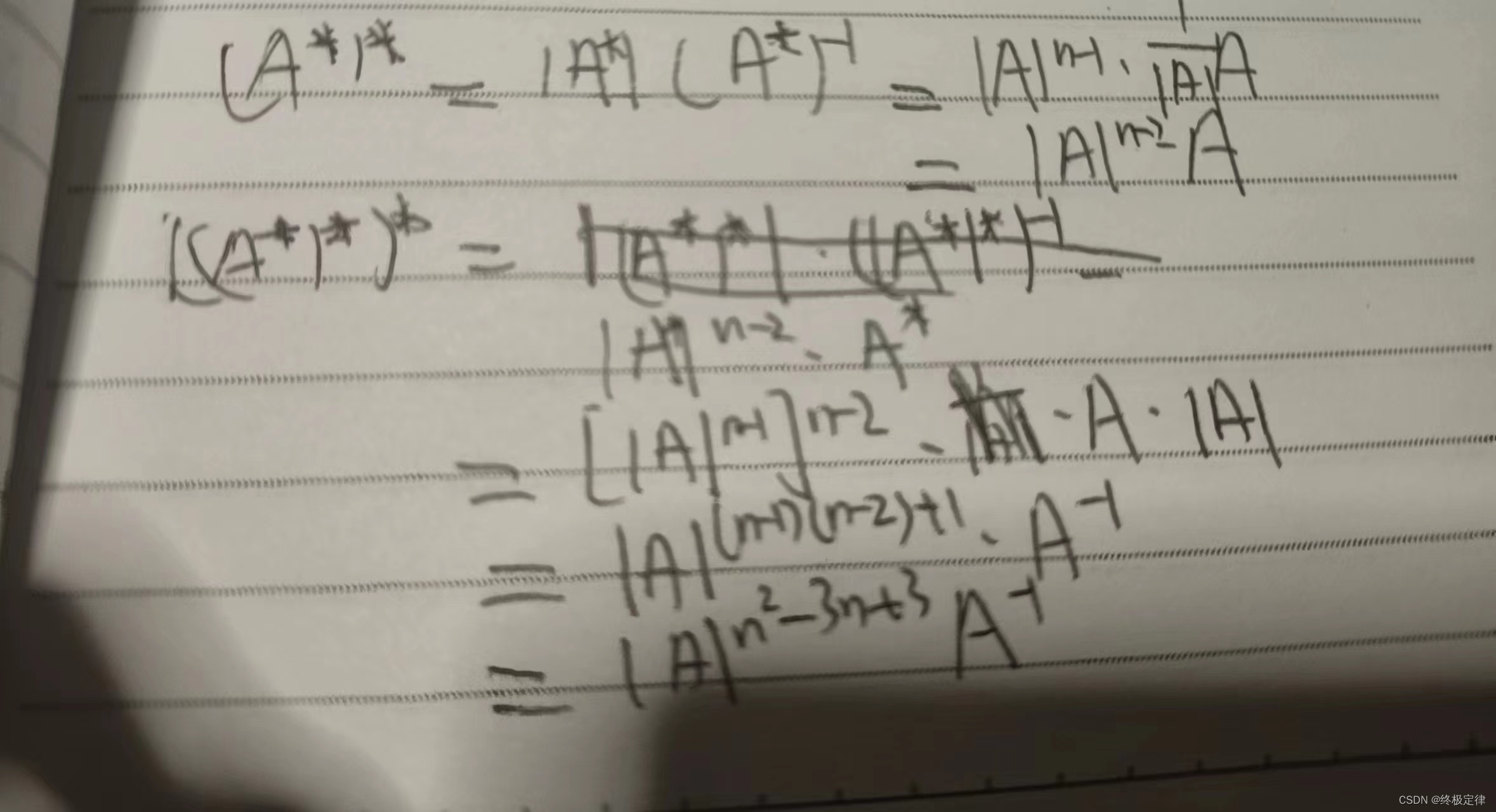
逆矩阵相关性质与例题
1.方阵的行列式:就是将方阵中的每一个元素转换至行列式中。 1.性质一:转置方阵的行列式等于转置前的行列式。(对标性质:行列式与它的转置行列式相等) 2.性质二:|ka||a|*k的n次方,n为方阵阶数。 …...

Ruoyi项目传List到后台并使用Excel模板下载数据的方法以及遇到的各种前后端数据交互问题
import { download } from @/utils/requestconst app = createApp(App)// 全局方法挂载 app.config.globalProperties.download = download 首先因为ruoyi-ui中的main.js有配置如上全局注册: 因此只需要在vue中定义一个方法直接使用this.download调用下载即可: (download的3…...

区块链技术将如何影响未来的数字营销?
你是否听腻了区块链和数字营销等流行语,却不明白它们对未来意味着什么?那么,准备好系好安全带吧,因为区块链技术将彻底改变我们对数字营销的看法。从建立消费者信任到提高透明度和效率,其可能性是无限的。 让我们来探…...

小程序wx:if和hidden的区别?
wx:if:wx:if 是一个完整的条件渲染指令,当它的表达式为真时,才会渲染该指令所在的元素。如果表达式的值为假,则不会渲染该元素。这意味着在表达式为假时,该元素及其子元素都不会被渲染,就像它们从未存在过一…...

分布式幂等
分布式幂等 在分布式系统、网络通信和数据库操作中,幂等性是一个非常重要的概念,特别是在面对可能发生网络故障、消息重复、或者系统崩溃等情况时。 举个简单的例子,考虑一个银行转账的操作。如果转账操作是幂等的,那么无论你执…...

大数据 DataX-Web 详细安装教程
目录 一、DataX-Web 介绍 1.1 DataX-Web 是什么 1.2 DataX-Web 架构 二、DataX-Web 安装部署 2.1 环境要求 2.2 安装 2.3 部署 2.4 数据库初始化 2.5 配置 2.6 启动服务 2.6.1 一键启动所有服务 2.6.2 一键取消所有服务 2.7 查看服务(注意!…...

CSS3媒体查询实现不同宽度的下不同内容的展示
文章目录 前言CSS3 多媒体查询实例520 到 699px 宽度 - 添加邮箱图标700 到 1000px - 添加文本前缀信息大于 1001px 宽度 - 添加邮件地址大于 1151px 宽度 - 添加图标代码后言 前言 hello world欢迎来到前端的新世界 😜当前文章系列专栏:CSS ὃ…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...
