数据结构-二叉树(1)
1.树概念及结构
1.1树的概念
树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。
1.有一个特殊的结点,称为根结点,根节点没有前驱结点。
2.除根节点外,其余结点被分成M(M>0)个互不相交的集合T1、T2、……、Tm,其中每一个集合Ti(1<= i<= m)又是一棵结构与树类似的子树。每棵子树的根结点有且只有一个前驱,可以有0个或多个后继。
3.因此,树是递归定义的。
 注意:树形结构中,子树之间不能有交集,否则就不是树形结构
注意:树形结构中,子树之间不能有交集,否则就不是树形结构

1.2 树的相关概念
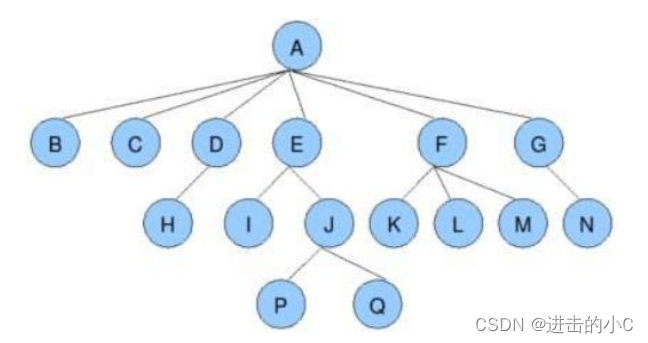
节点的度:一个节点含有的子树的个数称为该节点的度; 如上图:A的为6.
叶节点或终端节点:度为0的节点称为叶节点; 如上图:B、C、H、I...等节点为叶节点.
非终端节点或分支节点:度不为0的节点; 如上图:D、E、F、G...等节点为分支节点.
双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点; 如上图:A是B的父节点.
孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点; 如上图:B是A的孩子节点.
兄弟节点:具有相同父节点的节点互称为兄弟节点; 如上图:B、C是兄弟节点.
树的度:一棵树中,最大的节点的度称为树的度; 如上图:树的度为6.
节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推;
树的高度或深度:树中节点的最大层次; 如上图:树的高度为4.
堂兄弟节点:双亲在同一层的节点互为堂兄弟;如上图:H、I互为兄弟节点.
节点的祖先:从根到该节点所经分支上的所有节点;如上图:A是所有节点的祖先.
子孙:以某节点为根的子树中任一节点都称为该节点的子孙。如上图:所有节点都是A的子孙.
森林:由m(m>0)棵互不相交的树的集合称为森林;
1.3 树的表示
树结构相对线性表就比较复杂了,要存储表示起来就比较麻烦了,既然保存值域,也要保存结点和结点之间的关系,实际中树有很多种表示方式如:双亲表示法,孩子表示法、孩子双亲表示法以及孩子兄弟表示法等。我们这里就简单的了解其中最常用的孩子兄弟表示法.
typedef int DataType;
struct Node
{struct Node* _firstChild1; // 第一个孩子结点struct Node* _pNextBrother; // 指向其下一个兄弟结点DataType _data; // 结点中的数据域
};
2.二叉树概念及结构
2.1概念
一棵二叉树是结点的一个有限集合,该集合:
1. 或者为空
2. 由一个根节点加上两棵别称为左子树和右子树的二叉树组成

从上图可以看出:
1. 二叉树不存在度大于2的结点
2. 二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树
注意:对于任意的二叉树都是由以下几种情况复合而成的:
2.2 特殊的二叉树:
1. 满二叉树:一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。也就是说,如果一个二叉树的层数为K,且结点总数是 ,则它就是满二叉树。
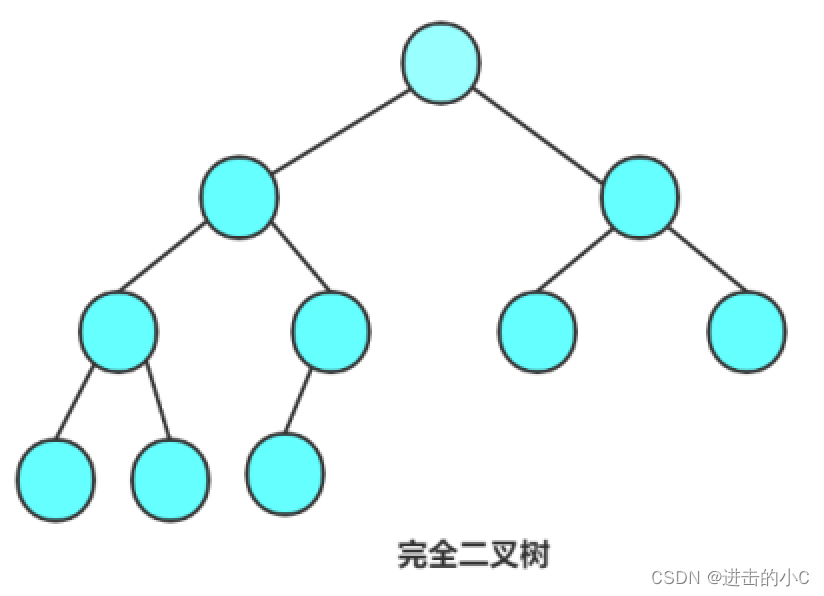
2. 完全二叉树:完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。

2.3二叉树的性质
1. 若规定根节点的层数为1,则一棵非空二叉树的第i层上最多有2^(i-1) 个结点.
2. 若规定根节点的层数为1,则深度为h的二叉树的最大结点数是2^h-1 .
3. 对任何一棵二叉树, 如果度为0其叶结点个数为 n0, 度为2的分支结点个数为n2 ,则有 n0=n2 +1
4. 若规定根节点的层数为1,具有n个结点的满二叉树的深度h= log2(n+1). (ps:log2(n+1) 是log以2为底,n+1为对数).
5. 对于具有n个结点的完全二叉树,如果按照从上至下从左至右的数组顺序对所有节点从0开始编号,则对于序号为i的结点有:1. 若i>0,i位置节点的双亲序号:(i-1)/2;i=0,i为根节点编号,无双亲节点
2. 若2i+1<n,左孩子序号:2i+1,2i+1>=n否则无左孩子
3. 若2i+2<n,右孩子序号:2i+2,2i+2>=n否则无右孩子
2.4 二叉树的存储结构
二叉树一般可以使用两种结构存储,一种顺序结构,一种链式结构。
1. 顺序存储
顺序结构存储就是使用数组来存储,一般使用数组只适合表示完全二叉树,因为不是完全二叉树会有空间的浪费。而现实中使用中只有堆才会使用数组来存储,关于堆我们后面的章节会专门讲解。二叉树顺序存储在物理上是一个数组,在逻辑上是一颗二叉树。
2. 链式存储
二叉树的链式存储结构是指,用链表来表示一棵二叉树,即用链来指示元素的逻辑关系。 通常的方法是链表中每个结点由三个域组成,数据域和左右指针域,左右指针分别用来给出该结点左孩子和右孩子所在的链结点的存储地址 。链式结构又分为二叉链和三叉链,当前我们学习中一般都是二叉链,后面课程学到高阶数据结构如红黑树等会用到三叉链。
3.二叉树的顺序结构及实现
3.1 二叉树的顺序结构
普通的二叉树是不适合用数组来存储的,因为可能会存在大量的空间浪费。而完全二叉树更适合使用顺序结构存储。现实中我们通常把堆(一种二叉树)使用顺序结构的数组来存储,需要注意的是这里的堆和操作系统虚拟进程地址空间中的堆是两回事,一个是数据结构,一个是操作系统中管理内存的一块区域分段。
3.2 堆的概念及结构
堆的性质:
堆中某个节点的值总是不大于或不小于其父节点的值;
堆总是一棵完全二叉树。
3.3 堆的实现
3.3.1堆的定义
堆的底层可以定义一个数组。
typedef int HPDataType;
typedef struct Heap
{HPDataType* a;int size;int capacity;
}HP;3.3.2堆的初始化
void HeapInit(HP* php)
{assert(php);php->a = NULL;php->size = 0;php->capacity = 0;
}3.3.3堆的销毁
void HeapDestroy(HP* php)
{assert(php);free(php->a);php->a = NULL;php->size = php->capacity = 0;
}3.3.4插入数据
首先判断一下空间是否满了,满了的话则扩容。再使用三目操作符判断是否是第一次扩容,再进行相应的扩容,再利用realloc的特点进行扩容或者是调整。在size位置上插入数据,再size++。但是现在不是堆,所以需要进行调整,使用向上调整。
void HeapPush(HP* php, HPDataType x)
{assert(php);// 扩容if (php->size == php->capacity){int newCapacity = php->capacity == 0 ? 4 : php->capacity * 2;HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * newCapacity);if (tmp == NULL){perror("realloc fail");exit(-1);}php->a = tmp;php->capacity = newCapacity;}php->a[php->size] = x;php->size++;AdjustUp(php->a, php->size - 1);
}3.3.5向上调整数据
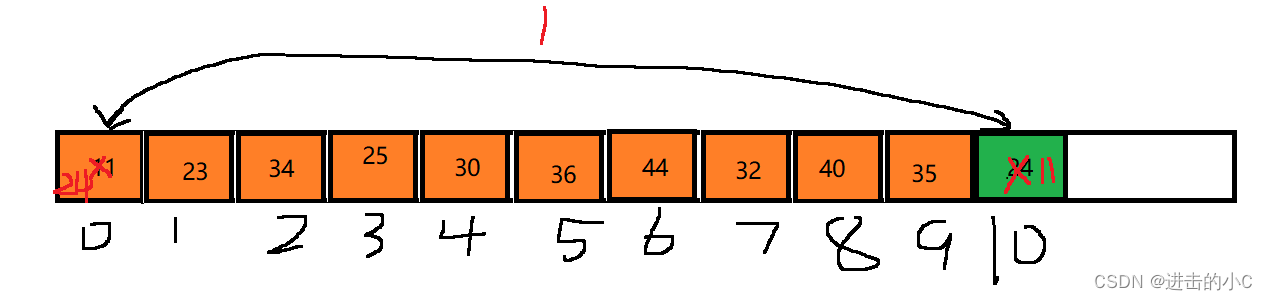
假设有一组这样的小堆数据,要插入一个20,再进行向上调整。

 第一步就是通过下标找到父亲节点parent=(child-1)/2,判断父亲节点是否小于此儿子节点,如果父亲节点小于此儿子节点,就不需要调整,否则就需要进行交换。交换完后将儿子下标child=parent,在下图中就是将10换成了4。再重新计算父亲下标,因为此时的parent还是4,所以parent=(parent-1)/2计算父亲下标,再向上判断,直到父亲节点小于儿子节点或者此节点调整到根节点。
第一步就是通过下标找到父亲节点parent=(child-1)/2,判断父亲节点是否小于此儿子节点,如果父亲节点小于此儿子节点,就不需要调整,否则就需要进行交换。交换完后将儿子下标child=parent,在下图中就是将10换成了4。再重新计算父亲下标,因为此时的parent还是4,所以parent=(parent-1)/2计算父亲下标,再向上判断,直到父亲节点小于儿子节点或者此节点调整到根节点。

 所以这个函数开始就要计算一下父亲节点,再进入while循环,循环结束的条件是child=0,也就是调整到了根节点这个位置。进入循环先判断儿子节点和父亲节点的大小,如果儿子节点小于父亲节点则开始交换,利用Swap函数交换值,再调整儿子节点的下标和父亲节点的下标,如果儿子节点大于父亲节点了也跳出循环。
所以这个函数开始就要计算一下父亲节点,再进入while循环,循环结束的条件是child=0,也就是调整到了根节点这个位置。进入循环先判断儿子节点和父亲节点的大小,如果儿子节点小于父亲节点则开始交换,利用Swap函数交换值,再调整儿子节点的下标和父亲节点的下标,如果儿子节点大于父亲节点了也跳出循环。
void Swap(HPDataType* p1, HPDataType* p2)
{HPDataType tmp = *p1;*p1 = *p2;*p2 = tmp;
}
void AdjustUp(HPDataType* a, int child)
{int parent = (child - 1) / 2;while (child > 0){if (a[child] < a[parent]){Swap(&a[child], &a[parent]);child = parent;parent = (parent - 1) / 2;}else{break;}}
}3.3.6打印堆
for循环写一个左闭右开即可,因为size-1才是最后一个数据的下标。
void HeapPrint(HP* php)
{assert(php);for (size_t i = 0; i < php->size; i++){printf("%d ", php->a[i]);}printf("\n");
}3.3.7向下调整数据
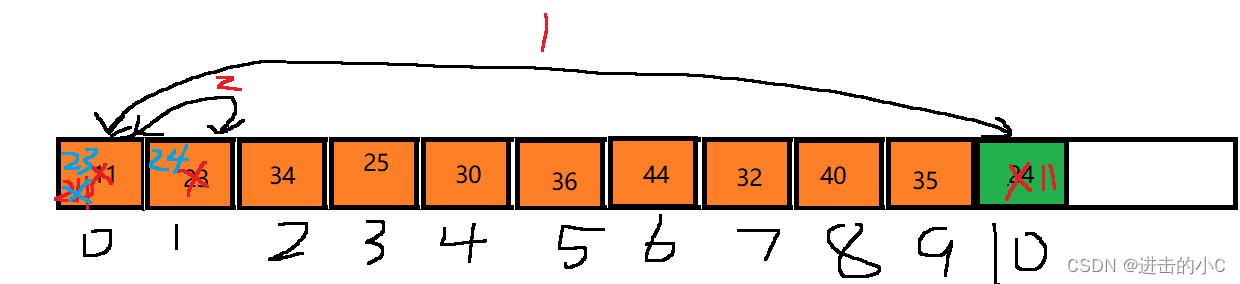
顺序表的尾删和尾插的效率是不错的,所以我们可以把尾节点和头节点交换位置,再size--删除掉尾节点。

这个时候还没有完,因为20这个数据如果放在头节点就不能保持这个小堆了,所以需要进行向下调整,向下调整就相当于找儿子节点child=parent*2+1,写一个while循环,结束条件是child=n越界,这个时候还要做一件事,就是找出左右孩子中较小的孩子,如果child+1<n&&左孩子小于右孩子有一个不成立则不需要找大小孩子了,也就是右孩子越界的话就结束,左孩子小于右孩子也结束。如果两个条件都成立的话则将child+1,换成左孩子小的右孩子。接下来判断孩子节点和父亲节点的大小,如果孩子节点比父亲节点小,则Swap交换值,再将父亲下标parent换成孩子下标child,再计算下一个儿子节点下标,因为此时的parent还是0,所以child=parent*2+1。如果孩子节点大于父亲节点则退出循环。、

void AdjustDown(HPDataType* a, int n, int parent)
{int child = parent * 2 + 1;while (child<n){//找小的孩子if (child + 1 < n && a[child] > a[child + 1]){child = child + 1;}if (a[child] < a[parent]){Swap(&a[child], &a[parent]);//继续往下调整parent = child;child = parent * 2 + 1;}else{break;}}
}3.3.8删除数据
先交换根节点和尾节点,size--,再向下调整。
void HeapPop(HP* php)
{assert(php);assert(php->size > 0);Swap(&php->a[0],&php->a[php->size - 1]);--php->size;AdjustDown(php->a, php->size, 0);
}3.3.9取根节点数据
HPDataType HeapTop(HP* php)
{assert(php);assert(php->size > 0);return php->a[0];
}3.3.10判断堆是否为空
bool HeapEmpty(HP* php)
{assert(php);return php->size == 0;
}今天的分享到这里就结束了,感谢大家的阅读!
相关文章:

数据结构-二叉树(1)
1.树概念及结构 1.1树的概念 树是一种非线性的数据结构,它是由n(n>0)个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。 1.有一个特殊的结点&…...
SpringBoot——国际化
优质博文:IT-BLOG-CN 一、Spring 编写国际化时的步骤 【1】编写国际化配置文件; 【2】使用ResourceBundleMessageSource管理国际化资源文件; 【3】在页面使用ftp:message取出国际化内容; 二、SpringBoot编写国际化步骤 【1】创…...
shell 条件语句 if case
目录 测试 test测试文件的表达式 是否成立 格式 选项 比较整数数值 格式 选项 字符串比较 常用的测试操作符 格式 逻辑测试 格式 且 (全真才为真) 或 (一真即为真) 常见条件 双中括号 [[ expression ]] 用法 &…...
C语言:写一个函数,实现3*3矩阵的转置(指针)
分析: 在主函数 main 中,定义一个 3x3 的整型数组 a,并定义一个指向整型数组的指针 p。然后通过循环结构和 scanf 函数,从标准输入中读取用户输入的 3x3 矩阵的值,并存储到数组 a 中。 接下来,调用 mov…...

STL pair源码分析
STL pair源码分析 pair是STL中提供的一个简单的struct,用来处理类型不同的一对值,是非常常用的数据结构。这一对值是以public的形式暴露出来的,直接通过first和second就能访问。我们以MSVC提供的STL源码为例,分析pair的具体实现。…...

【开源】基于Vue和SpringBoot的农家乐订餐系统
项目编号: S 043 ,文末获取源码。 \color{red}{项目编号:S043,文末获取源码。} 项目编号:S043,文末获取源码。 目录 一、摘要1.1 项目介绍1.2 项目录屏 二、功能模块2.1 用户2.2 管理员 三、系统展示四、核…...

MyBatis 操作数据库(入门)
一:MyBatis概念 (1)MyBatis 💗MyBatis是一款优秀的持久层框架,用于简化JDBC的开发 (2)持久层 1.持久层 💜持久层:持久化操作的层,通常指数据访问层(dao),是用来操作数据库的 2.持久层的规范 ①…...

JVM——垃圾回收器(G1,JDK9默认为G1垃圾回收器)
1.G1垃圾回收器 JDK9之后默认的垃圾回收器是G1(Garbage First)垃圾回收器。 Parallel Scavenge关注吞吐量,允许用户设置最大暂停时间 ,但是会减少年轻代可用空间的大小。 CMS关注暂停时间,但是吞吐量方面会下降。 而G1…...

多模态——使用stable-video-diffusion将图片生成视频
多模态——使用stable-video-diffusion将图片生成视频 0. 内容简介1. 运行环境2. 模型下载3. 代码梳理3.1 修改yaml文件中的svd路径3.2 修改DeepFloyDataFiltering的vit路径3.3 修改open_clip的clip路径3.4 代码总体结构 4. 资源消耗5. 效果预览 0. 内容简介 近期,…...
)
springboot(ssm网络相册 在线相册管理系统Java(codeLW)
springboot(ssm网络相册 在线相册管理系统Java(code&LW) 开发语言:Java 框架:ssm/springboot vue JDK版本:JDK1.8(或11) 服务器:tomcat 数据库:mysql 5.7(或8.0)…...

邮箱发送短信的多种方式
第一种:邮箱验证方法: 导入依赖: <!-- mail依赖(发送短信的依赖) --><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-mail</artifactId> &l…...
)
R语言——taxize(第五部分)
taxize(第五部分) 3. taxize 文档中译3.71. nbn_synonyms(从 NBN 返回具有给定 id 的分类群名称的所有同义词)3.72. ncbi_children(在 NCBI 中搜索类群的子类群)3.73. ncbi_downstream(检索 NCB…...

负载均衡lvs
简介 ipvsadm 是 Linux 内核中的 IP 虚拟服务器(IPVS)管理工具。IPVS是 Linux 内核提供的一种负载均衡解决方案,它允许将入站的网络流量分发到多个后端服务器,以实现负载均衡和高可用性。IPVS通过在内核中维护一个虚拟服务器表&a…...

【腾讯云云上实验室】探索向量数据库背后的安全监控机制
当今数字化时代,数据安全成为了企业和个人最为关注的重要议题之一。随着数据规模的不断增长和数据应用的广泛普及,如何保护数据的安全性和隐私性成为了迫切的需求。 今天,我将带领大家一起探索腾讯云云上实验室所推出的向量数据库,…...
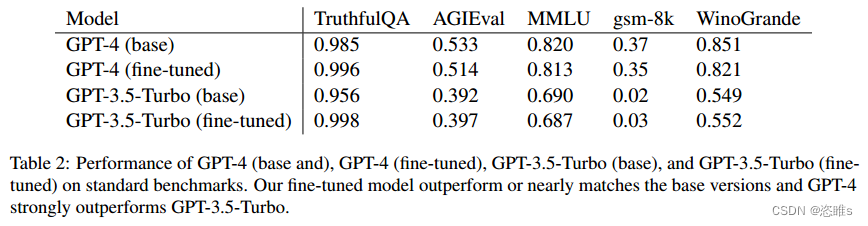
阅读笔记——《Removing RLHF Protections in GPT-4 via Fine-Tuning》
【参考文献】Zhan Q, Fang R, Bindu R, et al. Removing RLHF Protections in GPT-4 via Fine-Tuning[J]. arXiv preprint arXiv:2311.05553, 2023.【注】本文仅为作者个人学习笔记,如有冒犯,请联系作者删除。 目录 摘要 一、介绍 二、背景 三、方法…...

electron实现截图的功能
Electron是一种跨平台的桌面应用程序开发框架,可以使用HTML、CSS和JavaScript等Web技术构建桌面应用程序。下面是一种使用Electron实现截图的简单方法: 安装Electron和截图库 首先,需要安装Electron和一个截图库,例如electron-sc…...

11、动态数码管显示
数码管驱动方式 1、单片机直接扫描:硬件设备简单,但会消耗大量的单片机CPU时间 2、专用驱动芯片:内部自带显存、扫描电路,单片机只需告诉他显示什么即可 #include <REGX52.H> //数组代表显示亮灯的内容0、1、2、3、4、5、…...

Linux的基本指令(三)
目录 前言 echo指令(简述) Linux的设计理念 输出重定向操作符 > 追加输出重定向操作符 >> 输入重定向操作符 < 补充知识 学前补充 more指令 less指令 head指令 tail指令 查看文件中间的内容 利用输出重定向实现 利用管道“ |…...

使用python 实现华为设备的SFTP文件传输
实验目的: 公司有一台CE12800的设备,管理地址位172.16.1.2,现在需要编写自动化脚本,通过SFTP实现简单的上传下载操作。 实验拓扑: 实验步骤: 步骤1:将本地电脑和ensp的设备进行桥接ÿ…...

高防cdn防护原理是什么,是否可以防护服务器吗
随着互联网业务的迅速发展,网络安全问题日益凸显。在这样的背景下,高防CDN作为一种有效的网络安全解决方案,受到了越来越多的关注。那么高防CDN的防护原理是什么呢?接下来就跟小德一起深入了解下吧! 1. 高防CDN的基本概念 我们要明确什么是…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...

第7篇:中间件全链路监控与 SQL 性能分析实践
7.1 章节导读 在构建数据库中间件的过程中,可观测性 和 性能分析 是保障系统稳定性与可维护性的核心能力。 特别是在复杂分布式场景中,必须做到: 🔍 追踪每一条 SQL 的生命周期(从入口到数据库执行)&#…...

rknn toolkit2搭建和推理
安装Miniconda Miniconda - Anaconda Miniconda 选择一个 新的 版本 ,不用和RKNN的python版本保持一致 使用 ./xxx.sh进行安装 下面配置一下载源 # 清华大学源(最常用) conda config --add channels https://mirrors.tuna.tsinghua.edu.cn…...

密码学基础——SM4算法
博客主页:christine-rr-CSDN博客 专栏主页:密码学 📌 【今日更新】📌 对称密码算法——SM4 目录 一、国密SM系列算法概述 二、SM4算法 2.1算法背景 2.2算法特点 2.3 基本部件 2.3.1 S盒 2.3.2 非线性变换 编辑…...

数据库——redis
一、Redis 介绍 1. 概述 Redis(Remote Dictionary Server)是一个开源的、高性能的内存键值数据库系统,具有以下核心特点: 内存存储架构:数据主要存储在内存中,提供微秒级的读写响应 多数据结构支持&…...

【若依】框架项目部署笔记
参考【SpringBoot】【Vue】项目部署_no main manifest attribute, in springboot-0.0.1-sn-CSDN博客 多一个redis安装 准备工作: 压缩包下载:http://download.redis.io/releases 1. 上传压缩包,并进入压缩包所在目录,解压到目标…...
