136. 只出现一次的数字
136. 只出现一次的数字
题目:
给你一个 非空 整数数组 nums ,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。
你必须设计并实现线性时间复杂度的算法来解决此问题,且该算法只使用常量额外空间。
示例:
示例 1 :
输入:nums = [2,2,1]
输出:1
示例 2 :
输入:nums = [4,1,2,1,2]
输出:4
示例 3 :
输入:nums = [1]
输出:1
提示:
1 <= nums.length <= 3 * 104-3 * 104 <= nums[i] <= 3 * 104- 除了某个元素只出现一次以外,其余每个元素均出现两次。
解题:
如果不考虑时间复杂度和空间复杂度的限制方法有很多:
方法一:集合法
使用集合unordered_set存储数字。遍历数组中的每个数字,如果集合中没有该数字,则将该数字加入集合,如果集合中已经有该数字,则将该数字从集合中删除,最后剩下的数字就是只出现一次的数字。
class Solution {
public:int singleNumber(vector<int>& nums) {unordered_set<int> numSet;for(int num : nums) {// 如果集合中已经有当前数字,则从集合中删除if(numSet.find(num) != numSet.end()) {numSet.erase(num);} else {// 如果集合中没有当前数字,则加入集合numSet.insert(num);}}// 集合中剩下的就是只出现一次的数字return *numSet.begin();}
};
方法二:哈希表法
使用哈希表存储每个数字和该数字出现的次数。遍历数组即可得到每个数字出现的次数,并更新哈希表,最后遍历哈希表,得到只出现一次的数字。
class Solution {
public:int singleNumber(vector<int>& nums) {unordered_map<int,int> numCount;// 遍历数组,更新哈希表中数字的出现次数for(int num : nums) {numCount[num]++;}// 遍历哈希表,找到只出现一次的数字for(auto& pair : numCount) {if(pair.second == 1) {return pair.first;}}// 如果没有找到只出现一次的数字,返回默认值0return 0;}
};
方法三:元素之和两倍性质
由于集合保证元素无重复,所以使用集合unordered_set不重复的存储数组的元素,也就是每个元素只存储一次,重复的不存储,计算它们的和,就相当于所有数字的两倍之和。然后将原数组中的元素全部相加,就相当于只出现了一次的元素加上全部出现了两次的元素。如此看来,它们的差就是就差了一个只出现一次的元素了。
class Solution {
public:int singleNUmber(vector<int>& nums) {unordered_set<int> numSet;int sumSet = 0;int sumArray = 0;// 遍历数组,更新集合中的元素之和和数组中的元素之和for(int num : nums) {if(numSet.find(num) == numSet.end()) {numSet.insert(num);sumSet += num;}sumArray += num;}// 计算集合中的元素之和的两倍减去数组中的元素之和,得到只出现一次的数字return 2*sumSet - sumArray;}
};
上述三种解法都需要额外使用 O(n) 的空间,其中 n 是数组长度。
如何才能做到线性时间复杂度和常数空间复杂度呢?
方法四:位运算(线性时间复杂度,常数空间复杂度)
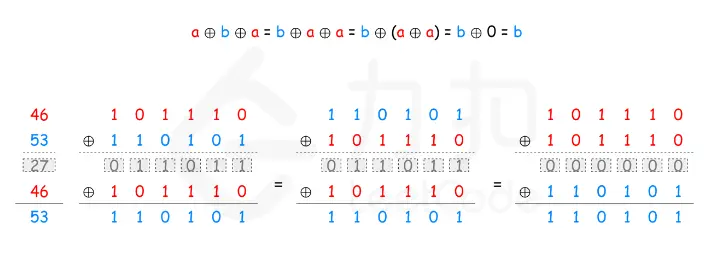
异或运算有以下三个性质:
-
任何数和 0 做异或运算,结果仍然是原来的数,即 a⊕0=a。
-
任何数和其自身做异或运算,结果是 0,即 a⊕a=0。
-
异或运算满足交换律和结合律,即 a⊕b⊕a=b⊕a⊕a=b⊕(a⊕a)=b⊕0=b。


假设数组中有 2m+1 个数,其中有 m 个数各出现两次,一个数出现一次。
令 a1 、a2 、…、am为出现两次的 m 个数,am+1为出现一次的数。
根据性质 3,数组中的全部元素的异或运算结果总是可以写成如下形式:
- (a1⊕a1)⊕(a2⊕a2)⊕⋯⊕(am⊕am)⊕am+1
根据性质 2 和性质 1,上式可化简和计算得到如下结果:
- 0⊕0⊕⋯⊕0⊕am+1=am+1
因此,数组中的全部元素的异或运算结果即为数组中只出现一次的数字。
class Solution {
public:int singleNumber(vector<int>& nums) {int ret = 0;for(auto e : nums) ret ^= e;return ret;}
};
复杂度分析
- 时间复杂度:O(n),其中 n 是数组长度。只需要对数组遍历一次。
nt>& nums) {
int ret = 0;
for(auto e : nums) ret ^= e;
return ret;
}
};
**复杂度分析**- 时间复杂度:O(n),其中 n 是数组长度。只需要对数组遍历一次。
- 空间复杂度:O(1)。
相关文章:

136. 只出现一次的数字
136. 只出现一次的数字 题目: 给你一个 非空 整数数组 nums ,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。 你必须设计并实现线性时间复杂度的算法来解决此问题,且该算法只使用常量额外空…...
redis的性能管理及集群架构(主从复制、哨兵模式)
一、redis的性能管理 1、内存指标info memory 内存指标(重要) used_memory:853736 数据占用的内存 used_memory_rss:10551296 redis向操作系统申请的内存 used_memory_peak:853736 redis使用内存的峰值 注:单位:字节 系…...
,反向最大匹配算法(BMM)和双向最大匹配算法(BM)原理及实现)
【自然语言处理】正向最大匹配算法(FMM),反向最大匹配算法(BMM)和双向最大匹配算法(BM)原理及实现
目录 一,正向最大匹配算法(FMM) 二,反向最大匹配算法(RMM) 一,正向最大匹配算法(FMM) 正向最大匹配分词(Forward maximum matching segmentation)通常简称为…...
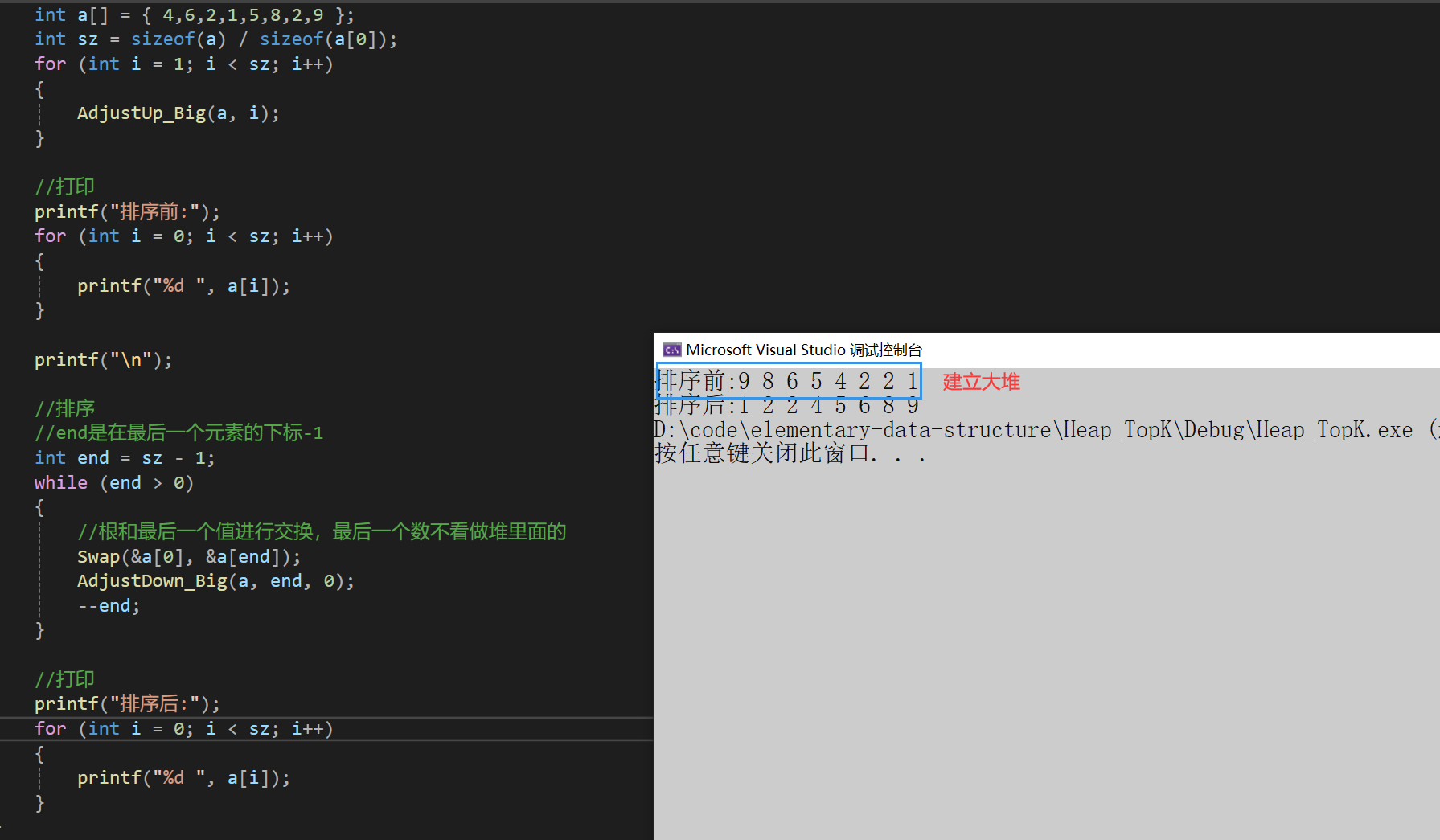
数据结构 | 堆排序
数据结构 | 堆排序 文章目录 数据结构 | 堆排序建立大堆排序结果以及全部代码 如果没有看过堆的实现的话可以先看前面的一章堆的实现,然后再来看这个堆排序,都是比较简单的~~ 这里堆排序首先建堆,建堆是要建小堆还是大堆呢? 在堆排…...

编程语言发展史:Go语言的设计和特点
一、前言 Go语言是一种由Google开发的编程语言,于2007年开始设计,2009年首次发布。Go语言是一种面向对象、静态类型、编译型的语言,具有高效、简单、安全等特点,可用于开发各种类型的应用程序。Go语言的设计和特点使其成为越来越…...

FinGPT:金融垂类大模型架构
Overview 动机 架构 底座模型: Llama2Chatglm2 Lora训练 技术路径 自动收集数据并整理 指令微调 舆情分析 搜新闻然后相似搜索 检索增强架构 智能投顾 Hugging face 地址 学术成果及未来方向 参考资料...
24. 深度学习进阶 - 矩阵运算的维度和激活函数
Hi,你好。我是茶桁。 咱们经过前一轮的学习,已经完成了一个小型的神经网络框架。但是这也只是个开始而已,在之后的课程中,针对深度学习我们需要进阶学习。 我们要学到超参数,优化器,卷积神经网络等等。看…...
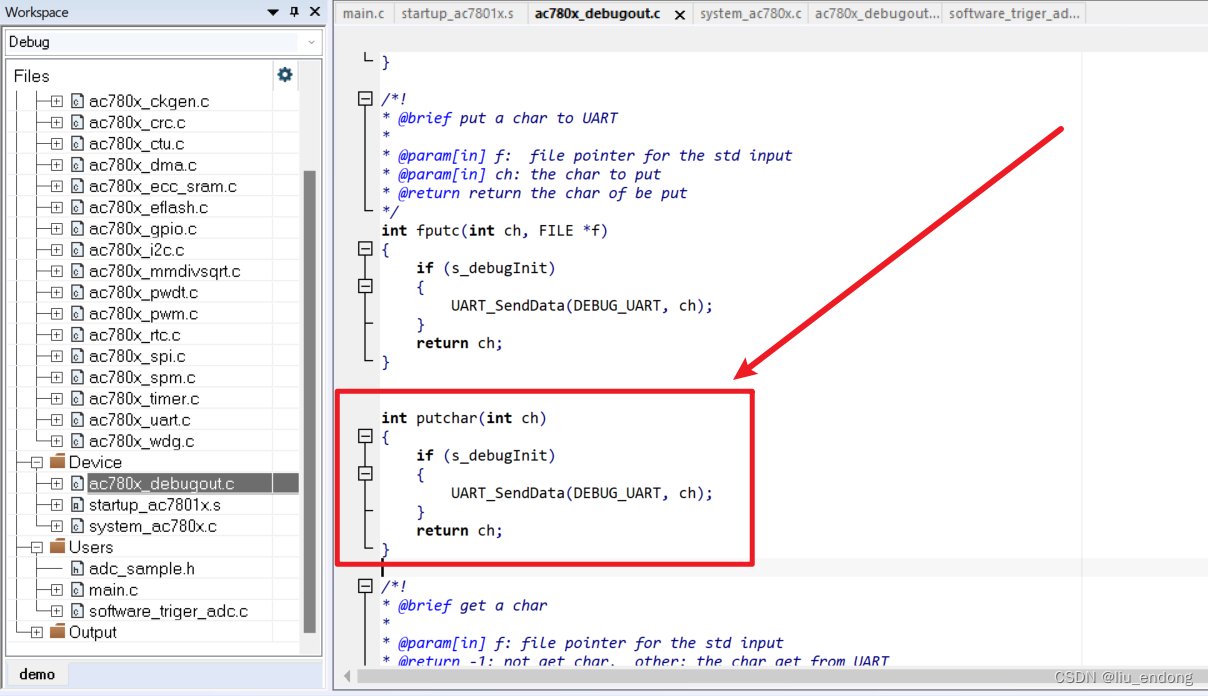
杰发科技AC7801——keil工程移植到IAR
0、简介 发现AC7801的代码只有keil工程的,IAR和Eclipse的代码只有一个例程,于是在从Keil移植到IAR时候遇到的问题记录下。 正常情况下,直接把keil的usr用户代码移植到iar的文件夹下面,删除原本的文件再添加新加进来的文件即可。…...
Word怎么看字数?简单教程分享!
“我在写文章时,总是想看看写了多少字。但是我发现我的Word无法看到字数。在Word中应该怎么查看字数呢?请帮帮我!” Word是一个广泛使用的文档编辑工具。在我们编辑文章时,如果想查看写了多少字,也是可以轻松完成的。 …...
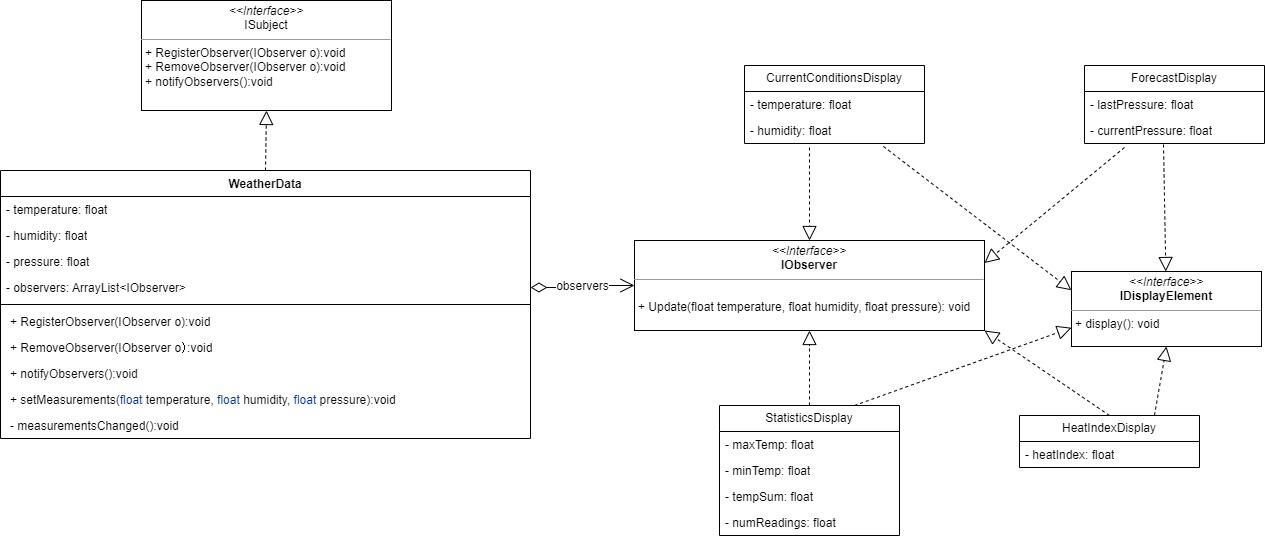
万字解析设计模式之观察者模式、中介者模式、访问者模式
一、观察者模式 1.1概述 观察者模式是一种行为型设计模式,它允许一个对象(称为主题或可观察者)在其状态发生改变时,通知它的所有依赖对象(称为观察者)并自动更新它们。这种模式提供了一种松耦合的方式&…...
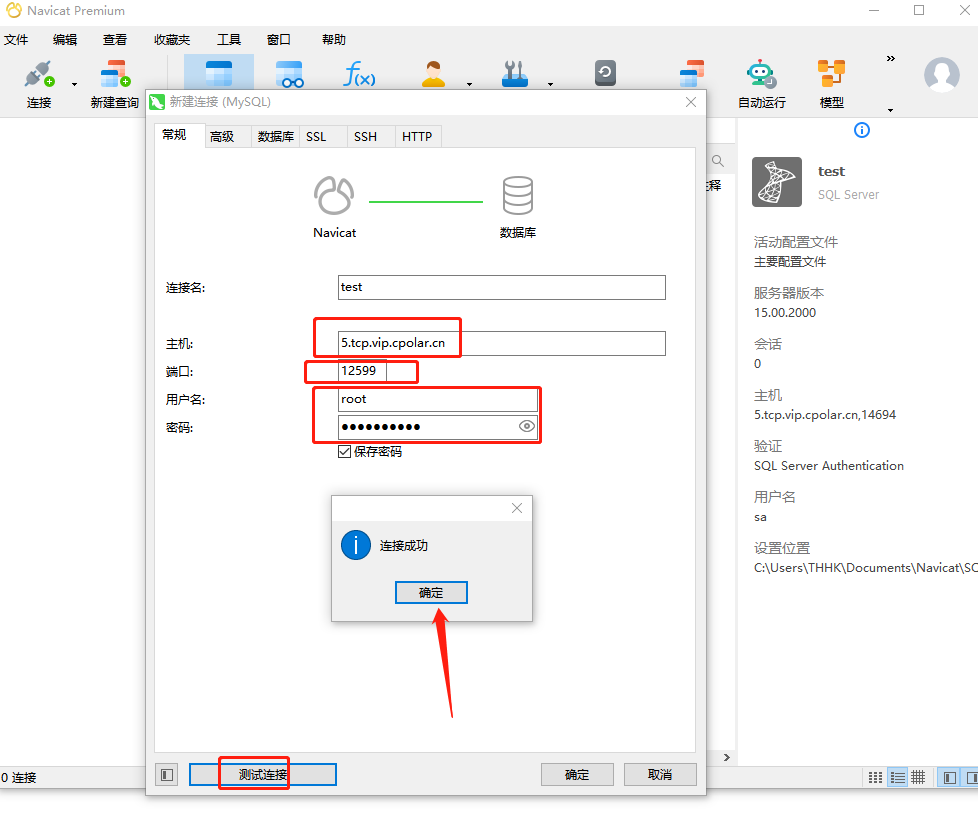
【MySQL | TCP】宝塔面板结合内网穿透实现公网远程访问
文章目录 前言1.Mysql服务安装2.创建数据库3.安装cpolar3.2 创建HTTP隧道4.远程连接5.固定TCP地址5.1 保留一个固定的公网TCP端口地址5.2 配置固定公网TCP端口地址 前言 宝塔面板的简易操作性,使得运维难度降低,简化了Linux命令行进行繁琐的配置&#x…...

Python break用法详解
Python 语言没有提供 goto 语句来控制程序的跳转,这种做法虽然提高了程序流程控制的可读性,但降低了灵活性。为了弥补这种不足,Python 提供了 continue 和 break 来控制循环结构。本节先讲解 break 的用法。 某些时候,需要在某种…...
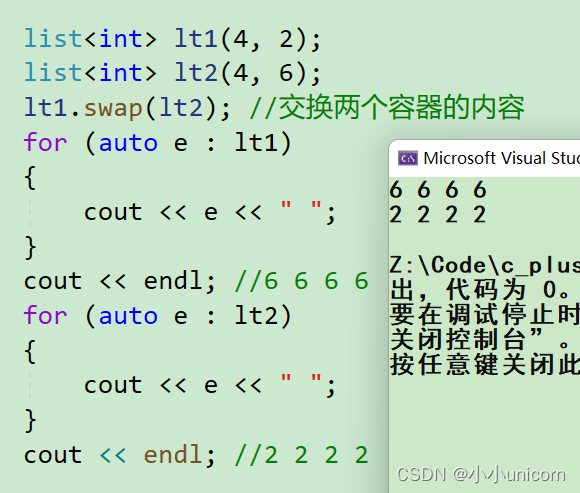
【C++初阶】STL详解(五)List的介绍与使用
本专栏内容为:C学习专栏,分为初阶和进阶两部分。 通过本专栏的深入学习,你可以了解并掌握C。 💓博主csdn个人主页:小小unicorn ⏩专栏分类:C 🚚代码仓库:小小unicorn的代码仓库&…...

MySQL特点和基本语句
MySQL MySQL是一种流行的关系型数据库管理系统,由瑞典MySQL AB公司开发,现属于甲骨文公司(Oracle)旗下产品。MySQL是基于C语言开发的,它具有高性能、可扩展性、易用性等特点,并且支持大量的用户访问。 My…...

Gin 学习笔记03-参数绑定
参数绑定 1、ShouldBindJSON2、ShouldBindQuery3、ShouldBindUri4、ShouldBind 1、ShouldBindJSON package mainimport ("github.com/gin-gonic/gin""net/http" )type User struct {Name string json:"name"Gender string json:"gender&…...

【100天精通Python】Day73:python机器学习入门算法详解与代码示例
目录 1. 监督学习算法: 1.1 线性回归(Linear Regression): 1.2 逻辑回归(Logistic Regression): 1.3 决策树(Decision Tree): 1.4 支持向量机ÿ…...
Node.js入门指南(四)
目录 express框架 express介绍 express使用 express路由 express 响应设置 中间件 路由模块化 EJS 模板引擎 express-generator hello,大家好!上一篇文章我们介绍了Node.js的模块化以及包管理工具等知识,这篇文章主要给大家分享Nod…...
Java LeetCode篇-深入了解关于数组的经典解法
🔥博客主页: 【小扳_-CSDN博客】 ❤感谢大家点赞👍收藏⭐评论✍ 文章目录 1.0 轮转数组 1.1 使用移位的方式 1.2 使用三次数组逆转法 2.0 消失的数字 2.1 使用相减法 2.2 使用异或的方式 3.0 合并两个有序数组 3.1 使用三指针方式 3.2 使用合…...
- 无重复字符的最长子串)
LeeCode前端算法基础100题(4)- 无重复字符的最长子串
一、问题详情: 给定一个字符串 s ,请你找出其中不含有重复字符的 最长子串 的长度。 示例 1: 输入: s "abcabcbb" 输出: 3 解释: 因为无重复字符的最长子串是 "abc",所以其长度为 3。示例 2: 输入: s "bbbbb…...

Axios简单使用与配置安装-Vue
安装Axios npm i axios main.js 导入 import Axios from axios Vue.prototype.$axios Axios简单发送请求 get getTest() {this.$axios({method: GET,url: https://apis.jxcxin.cn/api/title?urlhttps://apis.jxcxin.cn/}).then(res > {//请求成功回调console.log(res)}…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...
