【攻防世界-misc】Encode
1.下载解压文件,打开这个内容有些疑似ROT13加密,利用在线工具解密:ROT13解码计算器 - 计算专家
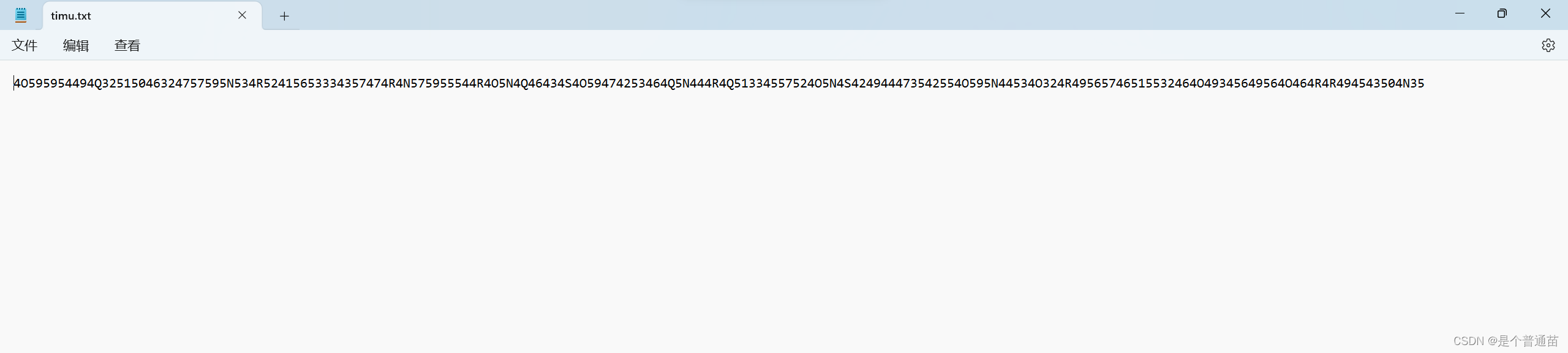
得到了解密后的值

得到解码结果后,看到是由数字和字母组成,再根据题目描述为套娃,猜测为base编码(有好多种),开始解密CTF在线工具-CTF工具|CTF编码|CTF密码学|CTF加解密|程序员工具|在线编解码
先用base16解码,得到一个结果
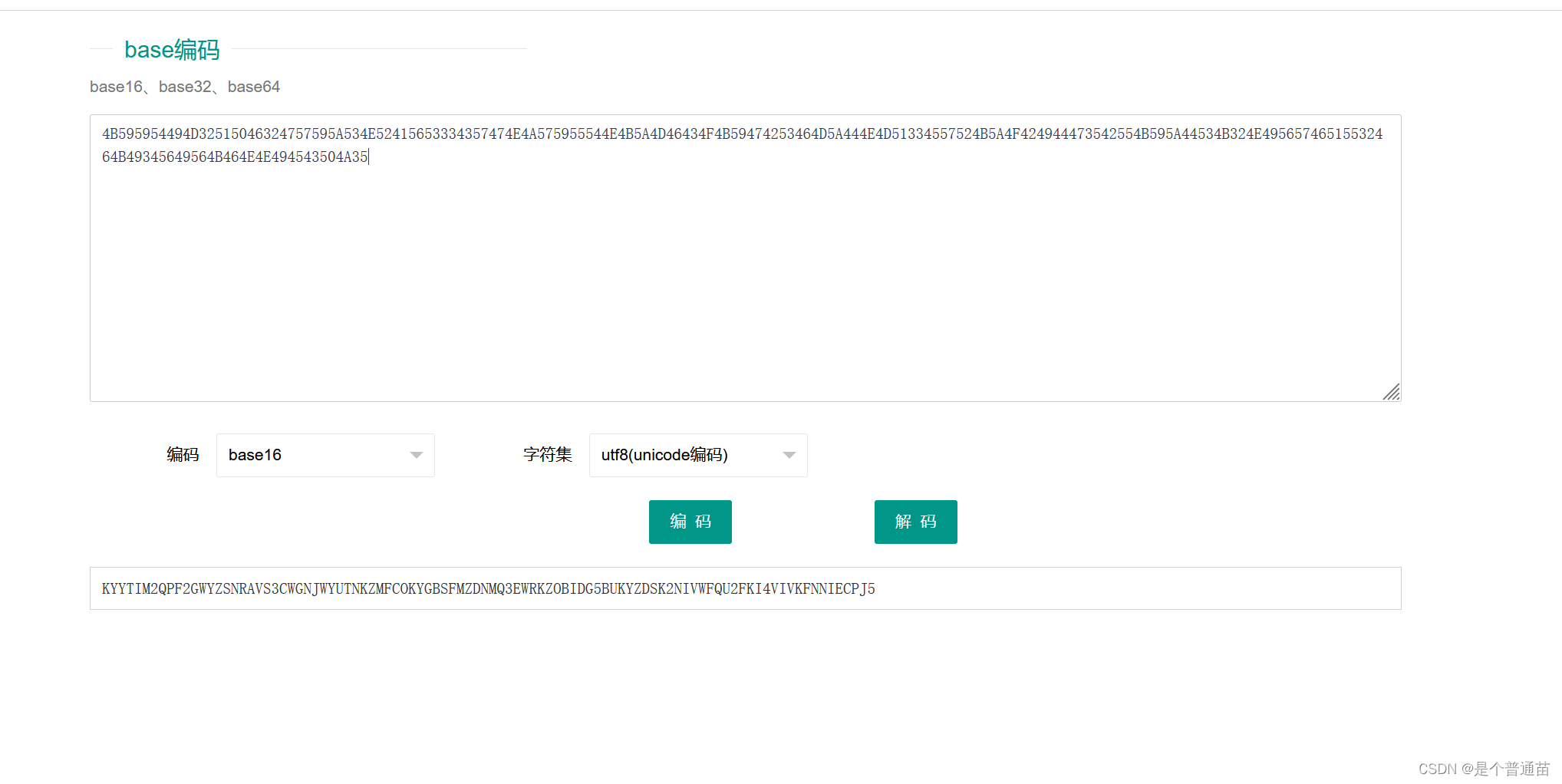
在将结果复制换成base32解密,
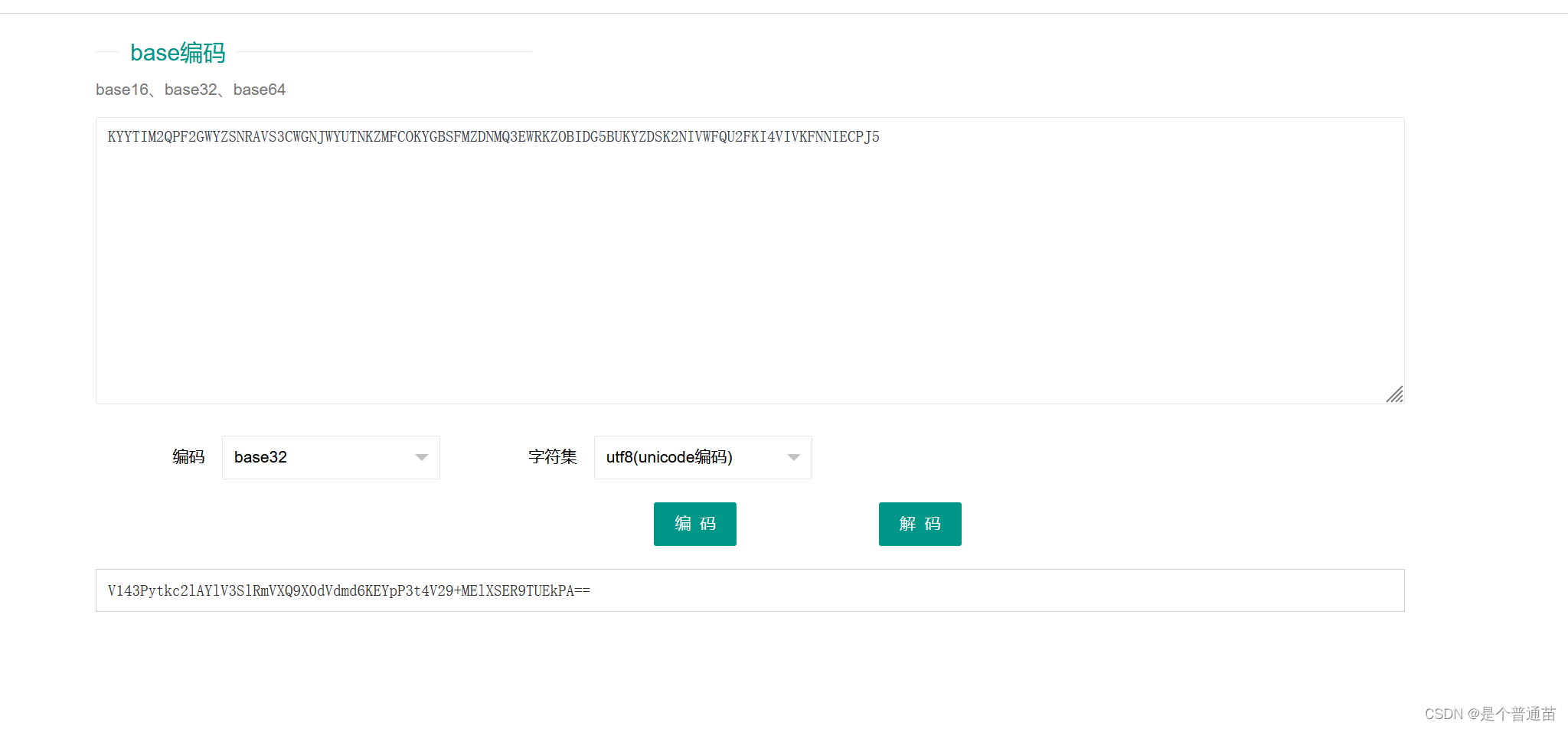
在将结果复制换成base64解密,
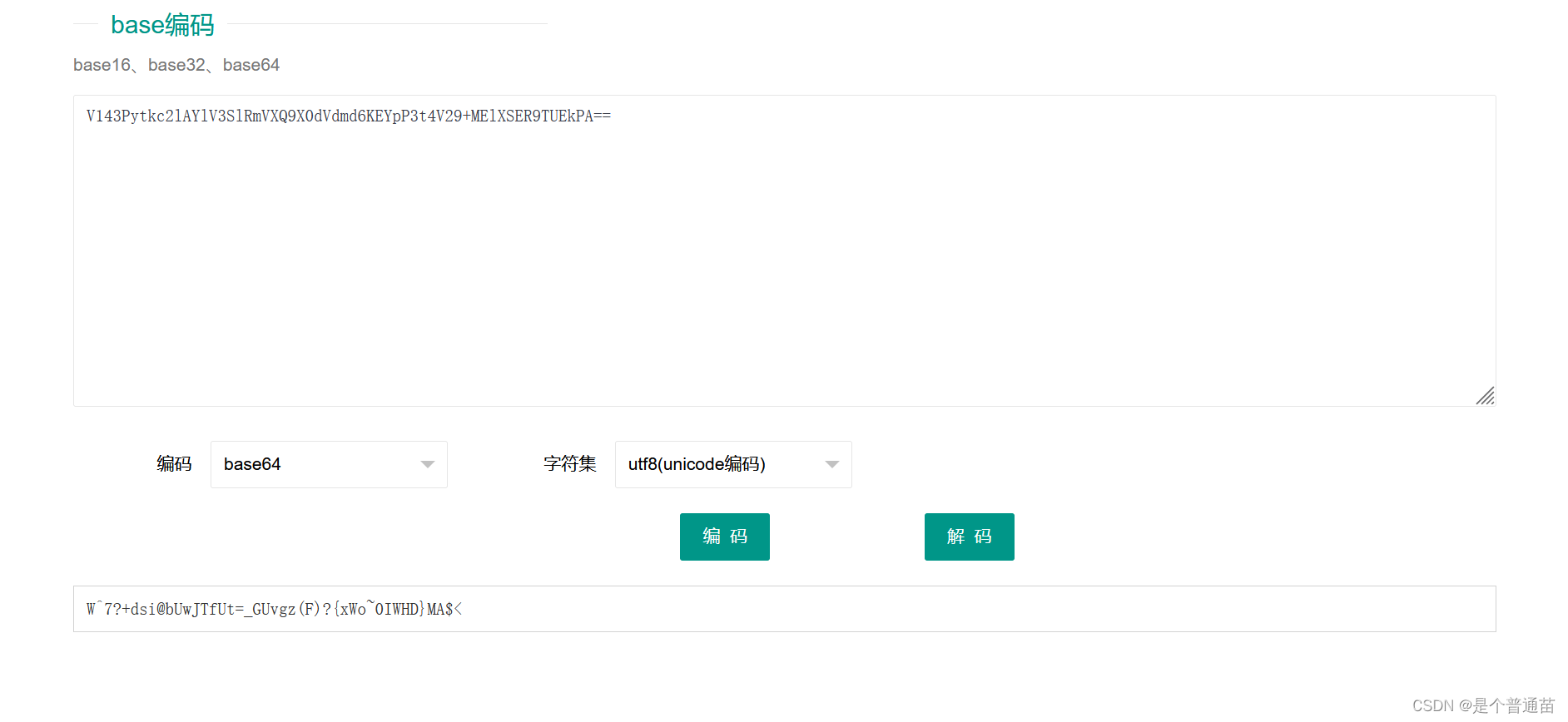
将得到的值进行解密,这里需要用到base85,但网站中的base85解不了,
方法一:用脚本运行,
import base64
x = "W^7?+dsi@bUwJTfUt=_GUvgz(F)?{xWo~0IWHD}MA$<"
y = base64.b85decode(x)
print(y)
方法二:https://tools.qsnctf.com/tools/Tools/Base85/index.php,进行解码
得到flag值:flag{W0w_y0u_c4n_rea11y_enc0d1ng!}
相关文章:

【攻防世界-misc】Encode
1.下载解压文件,打开这个内容有些疑似ROT13加密,利用在线工具解密:ROT13解码计算器 - 计算专家 得到了解密后的值 得到解码结果后,看到是由数字和字母组成,再根据题目描述为套娃,猜测为base编码(…...
visual c++ 2019 redistributable package
直接安装下面包只有24M Microsoft Visual C Redistributable 2019 x86: https://aka.ms/vs/16/release/VC_redist.x86.exe x64: https://aka.ms/vs/16/release/VC_redist.x64.exe ———————————————— 版权声明:本文为CSDN博主「kpacnB_Z」的原创文章…...

WPF中DataGrid解析
效果如图: 代码如下: <DataGrid Grid.Row"1" x:Name"dataGrid" ItemsSource"{Binding DataList}" AutoGenerateColumns"False"SelectedItem"{Binding SelectedItem,UpdateSourceTriggerPropertyChange…...
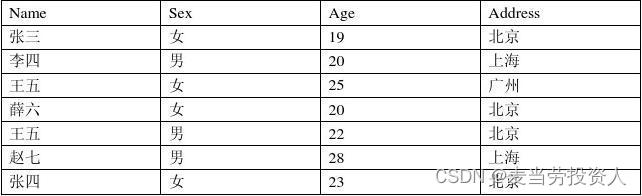
在数据库中进行表内容的修改(MYSQL)
根据表中内容,用命令语句创建数据库,表格,以及插入,修改,删除表格中的内容。 创建数据库:zrzy mysql> create database zrzy; 引用zrzy数据库: mysql> use zrzy; 创建student_info表&…...
Android中的多进程
在Android中也可以像pc一样开启多进程,这在android的编程中通常是比较少见的,以为在一个app基本上都是单进程工作就已经足够了,有一些特殊的场景,我们需要用多进程来做一些额外的工作,比如下载工作等。 在Android的An…...
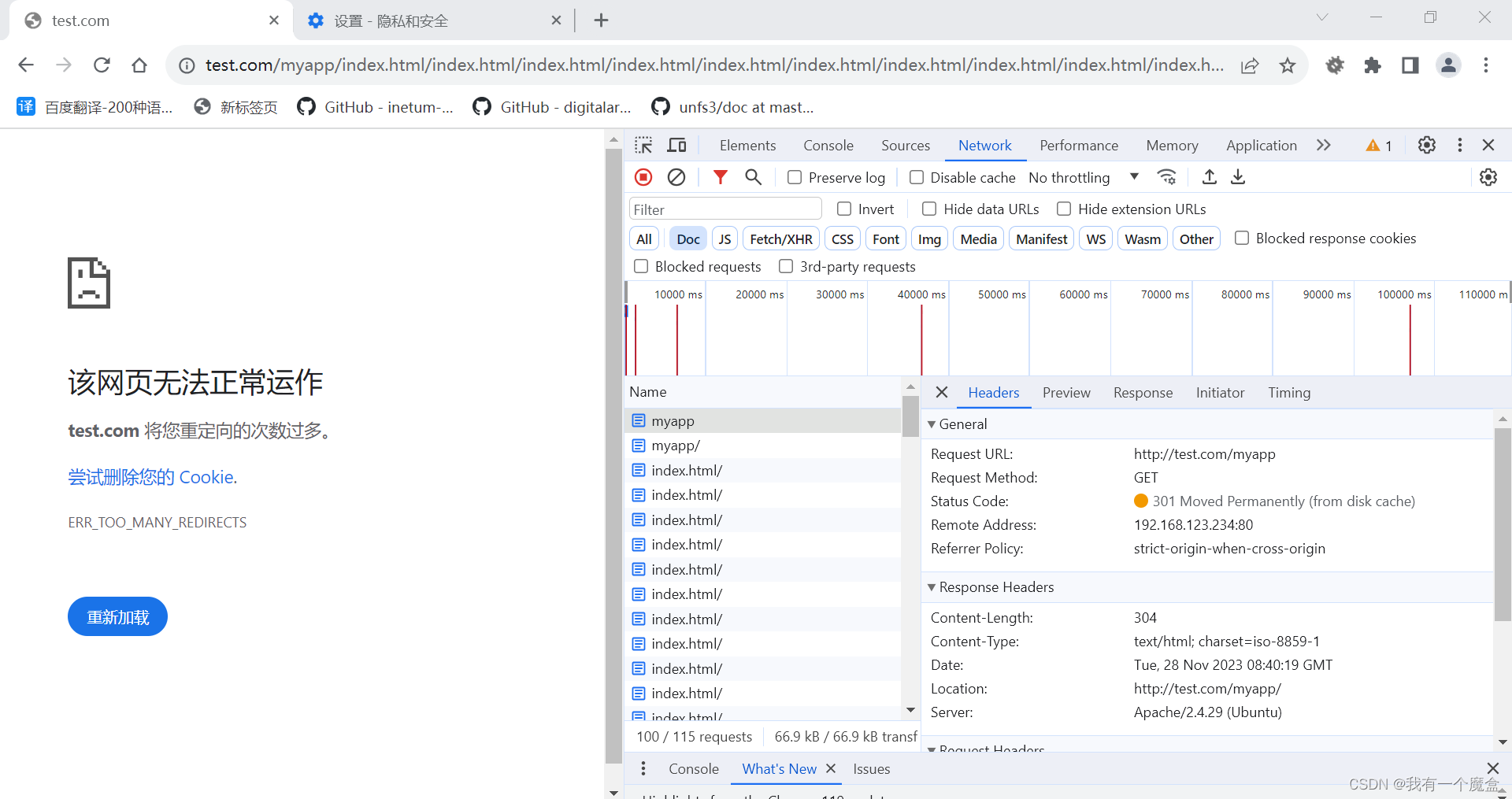
Apache2.4 AliasMatch导致301重定向问题?
环境:ubuntu18.04-desktop apache2版本: rootubuntu:/etc/apache2# apache2ctl -v Server version: Apache/2.4.29 (Ubuntu) Server built: 2023-03-08T17:34:33apache配置: DocumentRoot /var/www/html # Alias就没事 # Alias "/my…...

广州华锐视点:基于VR元宇宙技术开展法律法规常识在线教学,打破地域和时间限制
随着科技的飞速发展,人类社会正逐渐迈向一个全新的时代——元宇宙。元宇宙是一个虚拟的、数字化的世界,它将现实世界与数字世界紧密相连,为人们提供了一个全新的交流、学习和娱乐平台。在这个充满无限可能的元宇宙中,法律知识同样…...
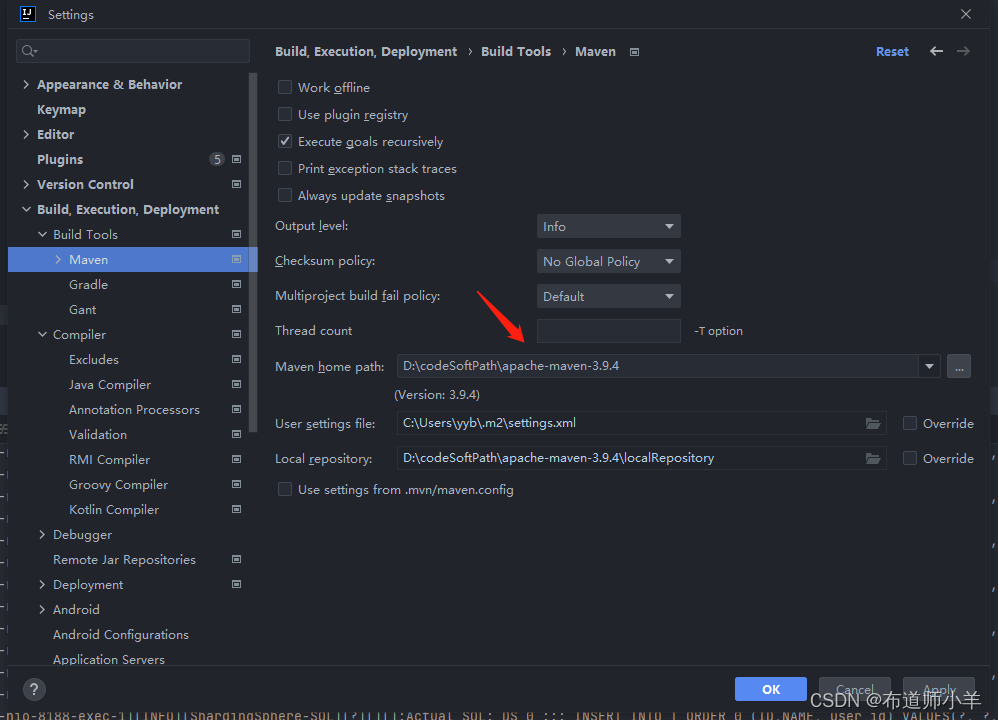
Maven——Maven使用基础
1、安装目录分析 1.1、环境变量MAVEN_HOME 环境变量指向Maven的安装目录,如下图所示: 下面看一下该目录的结构和内容: bin:该目录包含了mvn运行的脚本,这些脚本用来配置Java命令,准备好classpath和相关…...
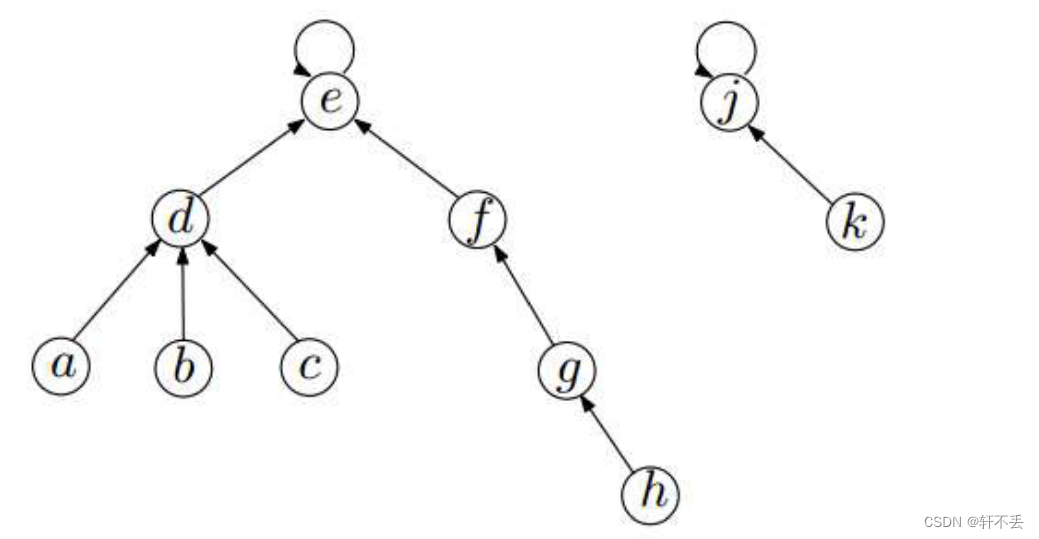
U4_2:图论之MST/Prim/Kruskal
文章目录 一、最小生成树-MST生成MST策略一些定义 思路彩蛋 二、普里姆算法(Prim算法)思路算法流程数据存储分析 伪代码时间复杂度分析 三、克鲁斯卡尔算法(Kruskal算法)分析算法流程并查集-Find-set 伪代码时间复杂度分析 一、最…...

springboot 注解@JsonInclude
修饰 实体属性or实体类 //枚举值:ALWAYS,NON_NULL,NON_ABSENT,NON_EMPTY,NON_DEFAULT,CUSTOM,USE_DEFAULTS JsonInclude(Include.NON_EMPTY)//将该标记放在属性上,如果该属性为NULL则不参与序列化 //如果放在类上边,那对这个类的全部属性起作用 Inclu…...

Python 中文完整教程目录
Python 教程 Python 是一门易于学习、功能强大的编程语言。它提供了高效的高级数据结构,还能简单有效地面向对象编程。Python 优雅的语法和动态类型以及解释型语言的本质,使它成为多数平台上写脚本和快速开发应用的理想语言。 Python 官网(…...

C/C++---------------LeetCode第35. 搜索插入位置
插入的位置 题目及要求二分查找在main内使用 题目及要求 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 示例 1: …...

网络安全--基于Kali的网络扫描基础技术
文章目录 1. 标准ICMP扫描1.1使用Ping命令1.1.1格式1.1.2实战 1.2使用Nmap工具1.2.1格式1.2.2实战1.2.2.1主机在线1.2.2.2主机不在线 1.3使用Fping命令1.3.1格式1.3.2实战 2. 时间戳查询扫描2.1格式2.2实战 3. 地址掩码查询扫描3.1格式3.2实战 2. TCP扫描2.1TCP工作机制2.2TCP …...
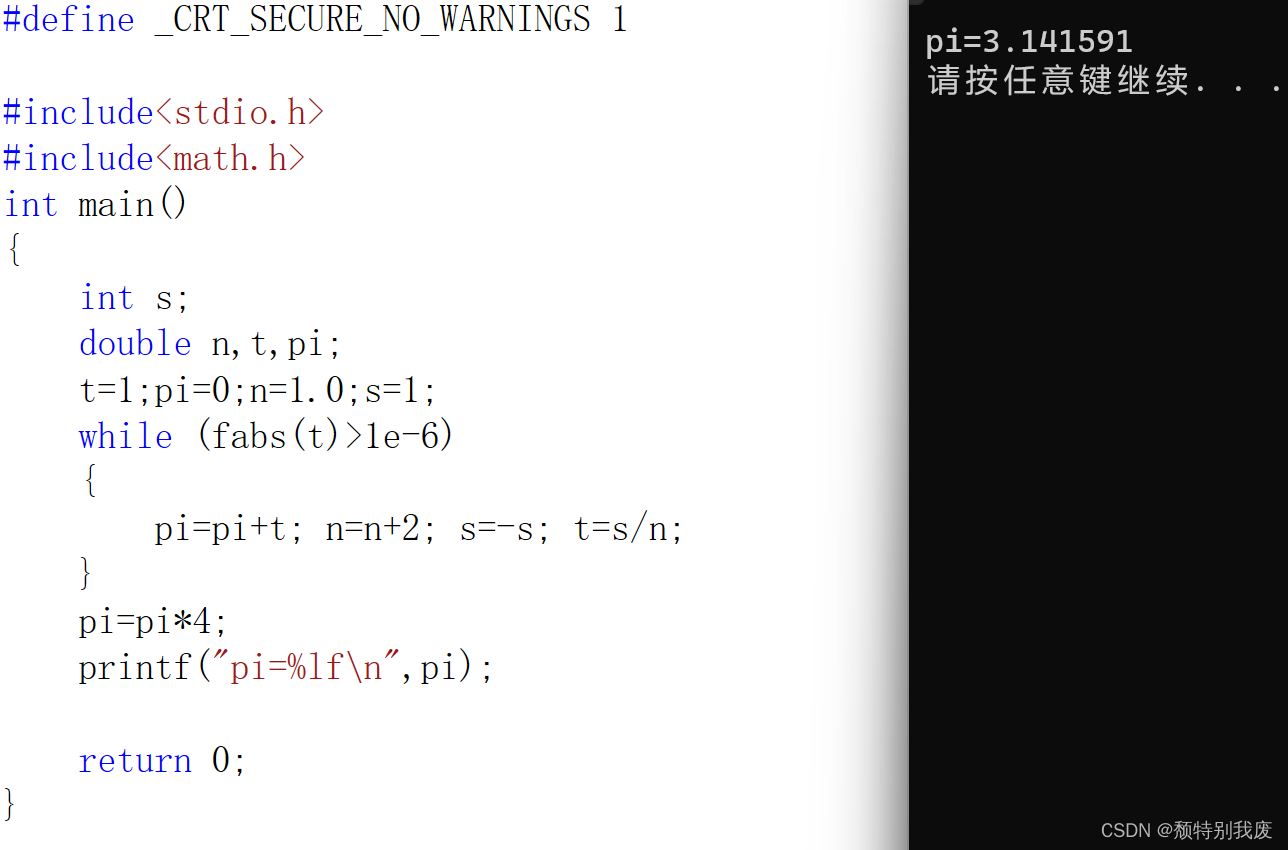
C语言——求π的近似值
#define _CRT_SECURE_NO_WARNINGS 1#include<stdio.h> #include<math.h> int main() {int s;double n,t,pi;t1;pi0;n1.0;s1;while (fabs(t)>1e-6){pipit; nn2; s-s; ts/n;}pipi*4;printf("pi%lf\n",pi);return 0; }这里是求小数点后6位——1e-6&#…...

如何使用ffmpeg转换图片格式
ffmpeg简介与图片格式介绍 windows安装ffmpeg,从如下网站下载release版本 https://www.gyan.dev/ffmpeg/builds/ ffmpeg 6.1版本仍然不支持heic的图片格式,未来可能会支持,具体见该issue: https://trac.ffmpeg.org/ticket/6521 …...

11 动态规划解最后一块石头的重量II
来源:LeetCode第1049题 难度:中等 描述:有一堆石头,用证书数组stones表示,其中stones[i]表示第i块石头的重量,每一回合,从中选出任意两块石头,然后将他们放在一起粉碎,…...
|LeetCode121. 买卖股票的最佳时机、LeetCode122. 买卖股票的最佳时机 II)
LeetCode算法题解(动态规划,股票买卖)|LeetCode121. 买卖股票的最佳时机、LeetCode122. 买卖股票的最佳时机 II
一、LeetCode121. 买卖股票的最佳时机 题目链接:121. 买卖股票的最佳时机 题目描述: 给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。 你只能选择 某一天 买入这只股票,并选择在 未来的某一…...

python实验3 石头剪刀布游戏
实验3:石头剪刀布游戏 一、实验目的二、知识要点图三、实验1. 石头剪刀布2. 实现大侠个人信息 一、实验目的 了解3类基本组合数据类型。理解列表概念并掌握Python中列表的使用。理解字典概念并掌握Python中字典的使用。运用jieba库进行中文分词并进行文本词频统计。…...

米贸搜|如何设置 Facebook 转换 API + 事件重复数据删除
Facebook Pixel 可让您跟踪用户在您网站上的行为、收集再营销受众并创建相似对象。如果 Facebook 像素实现正确,它将向 FB 机器学习算法提供相关信息。 FB ML 将使用像素数据向最有可能转化的人展示您的广告。 几年来,我们可以通过 JavaScript 代码、应…...

python每日一题——11滑动窗口最大值
题目 给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。返回滑动窗口中的最大值 。 示例 1: 输入:nums [1,3,-1,-3,5,3,6,7], k 3…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...

k8s从入门到放弃之HPA控制器
k8s从入门到放弃之HPA控制器 Kubernetes中的Horizontal Pod Autoscaler (HPA)控制器是一种用于自动扩展部署、副本集或复制控制器中Pod数量的机制。它可以根据观察到的CPU利用率(或其他自定义指标)来调整这些对象的规模,从而帮助应用程序在负…...

热烈祝贺埃文科技正式加入可信数据空间发展联盟
2025年4月29日,在福州举办的第八届数字中国建设峰会“可信数据空间分论坛”上,可信数据空间发展联盟正式宣告成立。国家数据局党组书记、局长刘烈宏出席并致辞,强调该联盟是推进全国一体化数据市场建设的关键抓手。 郑州埃文科技有限公司&am…...
