数据结构-01-数组
每一种编程语言中,基本都会有数组这种数据类型。不过,它不仅仅是一种编程语言中的数据类型,还是一种最基础的数据结构。
1-数组的概念和特性
数组(Array)是一种线性表数据结构。它用一组连续的内存空间,来存储一组具有相同类型的数据。
线性表(Linear List)就是数据排成像一条线一样的结构。每个线性表上的数据最多只有前和后两个方向。其实除了数组,链表、队列、栈等也是线性表结构。
连续的内存空间和相同类型的数据。正是因为这两个限制,它才有了一个堪称"杀手锏"的特性:"随机访问"。a[0]就是偏移为0的位置,也就是首地址,a[k]就表示偏移k个type_size的位置,所以计算a[k]的内存地址只需要用这个公式:a[k]_address = base_address + k * type_size
查询:数组支持随机访问,根据下标随机访问的时间复杂度为O(1)。查找的时间复杂度并不为O(1)。即便是排好序的数组,你用二分查找,时间复杂度也是O(logn)。
插入:假设数组的长度为n,现在,如果我们需要将一个数据插入到数组中的第k个位置。为了把第k个位置腾出来,给新来的数据,我们需要将第k~n这部分的元素都顺序地往后挪一位。如果在数组的末尾插入元素,那就不需要移动数据了,这时的时间复杂度为O(1)。但如果在数组的开头插入元素,那所有的数据都需要依次往后移动一位,所以最坏时间复杂度是O(n)。 因为我们在每个位置插入元素的概率是一样的,所以平均情况时间复杂度为(1+2+…n)/n=O(n)。
删除:如果我们要删除第k个位置的数据,为了内存的连续性,也需要搬移数据,不然中间就会出现空洞,内存就不连续了。如果删除数组末尾的数据,则最好情况时间复杂度为O(1);如果删除开头的数据,则最坏情况时间复杂度为O(n);平均情况时间复杂度也为O(n)。
思想:在某些特殊场景下,我们并不一定非得追求数组中数据的连续性。如果我们将多次删除操作集中在一起执行,删除的效率会高很多;比如JVM标记清除垃圾回收算法的核心思想 就是标记一下,然后一起删除。
2-高级语言的封装
针对数组类型,很多语言都提供了容器类,比如Java中的ArrayList;ArrayList最大的优势就是可以将很多数组操作的细节封装起来和支持动态扩容。
对比容器和数组优缺点:
(1)Java ArrayList无法存储基本类型,比如int、long,需要封装为Integer、Long类,而Autoboxing、Unboxing则有一定的性能消耗,所以如果特别关注性能,或者希望使用基本类型,就可以选用数组。
(2)如果数据大小事先已知,并且对数据的操作非常简单,用不到ArrayList提供的大部分方法,也可以直接使用数组。
(3)当要表示多维数组时,用数组往往会更加直观。比如Object[][] array;而用容器的话则需要这样定义:ArrayList<ArrayList > array。
对于业务开发,直接使用容器就足够了,省时省力。毕竟损耗一丢丢性能,完全不会影响到系统整体的性能。但如果你是做一些非常底层的开发,比如开发网络框架,性能的优化需要做到极致,这个时候数组就会优于容器,成为首选。
相关文章:

数据结构-01-数组
每一种编程语言中,基本都会有数组这种数据类型。不过,它不仅仅是一种编程语言中的数据类型,还是一种最基础的数据结构。 1-数组的概念和特性 数组(Array)是一种线性表数据结构。它用一组连续的内存空间,来…...

甘草书店记: 2023年10月11日 星期三 晴 「做有光的人,照亮他人,也引人同行」
发了两篇《甘草书店记》,书店计划公之于众,收获了不少人的赞扬和鼓励,来自生活中的友人,来自麦田的客户和朋友,来自图书界的同行前辈,也来自商界的同仁。其中,最特别留言来自甘草书店投资方的张…...

让 OpenAI GPT4 出 10 道题测试其他开源大语言模型
让 OpenAI GPT4 出 10 道题测试其他开源大语言模型 1. 中文题目及答案2. 日文题目及答案3. 英文题目及答案 1. 中文题目及答案 数学题:一个矩形的长是10厘米,宽是5厘米,求它的面积。 答案:面积 长 x 宽 10厘米 x 5厘米 50平方厘…...

动态库与静态库
1. 库 是代码的二进制的封装形式 在其他的源代码或库中,可以直接调用库的,但是又看不到它 没有公开源代码 库的这种实现方法有利于模块化 而且只要接口合理 不影响库的使用的 sum.c sum.h int sum(int a,int b) { return ab; } xxx.c 需要使用…...
pdf文件编辑,[增删改查]
pdf文件是投标文件中必不可少的格式,传统的方式先编辑word格式,最后生成pdf,但是有时候需要直接编辑pdf文件,编辑pdf的工具无疑 “adobe acrobat dc”是最好用的之一了 1.把图片文件添加到pdf指定位置,例如把一张图片添…...
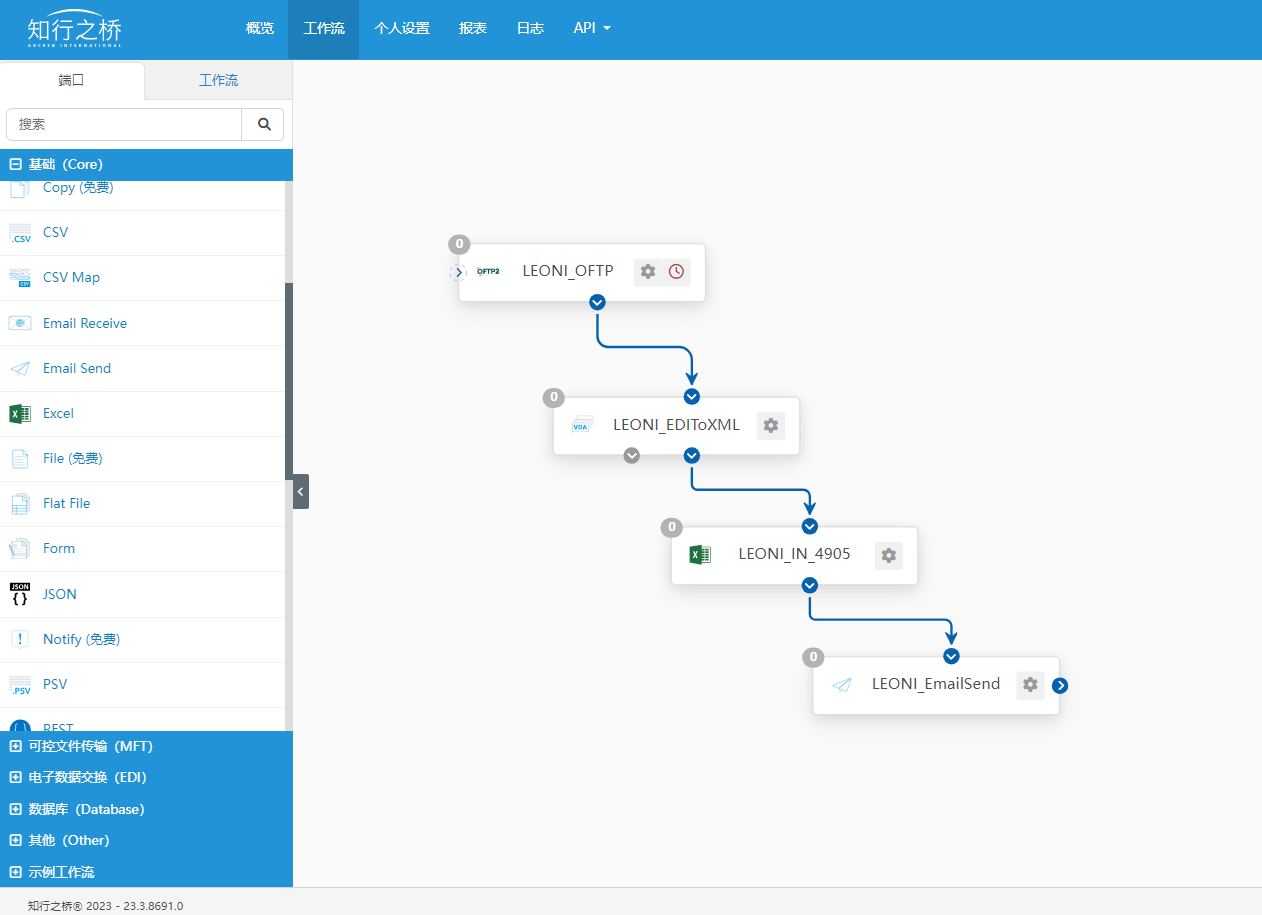
如何与LEONI建立EDI连接?
莱尼LEONI是一家为汽车及其他行业提供能源数据管理产品、解决方案及服务的全球供应商。供应链范围从研发生产标准化电缆、特种电缆和数据电缆到高度复杂的布线系统和相关组件。本文将介绍如何与莱尼LEONI建立EDI连接。 什么是EDI? EDI全称Electronic Data Interch…...
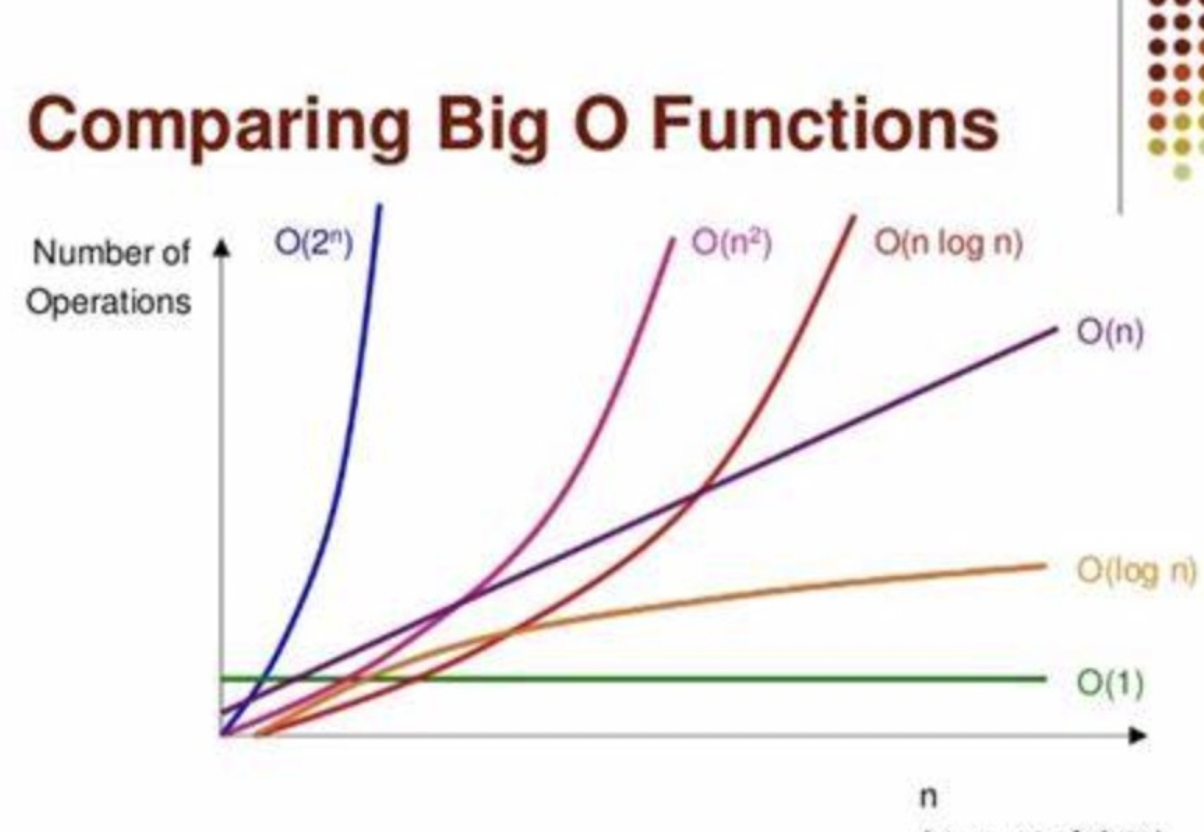
算法中的时间复杂度,空间复杂度
一、前言 算法(Algorithm)是指用来操作数据、解决程序问题的一组方法。对于同一个问题,使用不同的算法,也许最终得到的结果是一样的,但在过程中消耗的资源和时间却会有很大的区别 衡量不同算法之间的优劣主要是通过时…...

Python基础:推导式(Comprehensions)详解
1. 推导式概念 Python推导式(comprehensions)是一种简洁而强大的语法,用于从已存在的数据(列表、元组、集合、字典等)中创建新的数据结构。推导式包括: 列表推导式元组推导式字典推导式集合推导式 2. 列表…...
安防监控视频融合平台EasyCVR定制化页面开发
安防监控EasyCVR视频汇聚平台基于云边端智能协同,支持海量视频的轻量化接入与汇聚、转码与处理、全网智能分发、视频集中存储等。安防视频平台EasyCVR拓展性强,视频能力丰富,具体可实现视频监控直播、视频轮播、视频录像、云存储、回放与检索…...
Roll-A-Ball 游戏
Roll-A-Ball 游戏 1)学习资料 b站视频教程:https://www.bilibili.com/video/BV18W411671S/文档: * Roll-A-Ball 教程(一), * Roll-A-Ball 教程(二)线上体验roll-a-ball成品 * http://www-personal.umich.e…...
医疗影像数据集—CT、X光、骨折、阿尔茨海默病MRI、肺部、肿瘤疾病等图像数据集
最近收集了一大波关于CT、X光等医疗方面的数据集包含骨折、阿尔茨海默病MRI、肺部疾病等类型的医疗影像数据,废话不多说,给大家逐一介绍!! 1、彩色预处理阿尔茨海默病MRI(磁共振成像)图像数据集 彩色预处理阿尔茨海默病MRI(磁共…...
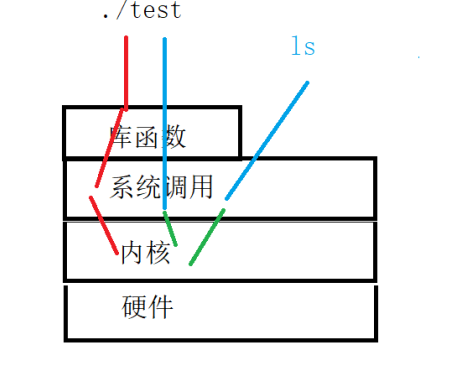
Linux僵死进程及文件操作
1.僵死进程(僵尸进程): 1.僵死进程产生的原因或者条件: 什么是僵死进程? 当子进程先于父进程结束,父进程没有获取子进程的退出码,此时子进程变成僵死进程. 简而言之,就是子进程先结束,并且父进程没有获取它的退出码; 那么僵死进程产生的原因或者条件就是:子进…...

用Python写一个浏览器集群框架
更多Python学习内容:ipengtao.com 在分布式爬虫和大规模数据采集的场景中,使用浏览器集群是一种有效的方式,可以提高数据采集的速度和效率。本文将介绍如何用Python编写一个简单但强大的浏览器集群框架,以应对需要使用多个浏览器实…...

【Github】git安装
我们经常需要对github上的项目进行复现或者使用,git指令可以方便我们更好地实现他们。 Part 0. 准备 配置代理IP 面对问题:关于登陆github网站网速慢、下载git项目网速慢。 解决:无论是windows还是linux系统,都可以找到/etc/ho…...
sql语法大全
1,创建数据库 create database 数据库名字; 2,查看所有的数据库名称 show databases; MySQL服务器已有4个数据库,这些数据库都是MySQL安装时自动创建的。 information_schema 和 performance_schema 数据库分别是 MySQL 服务器的数据字典(…...

小红书API接口测试 | 小红书笔记详情 API 接口测试指南
一、引言 随着互联网的发展,越来越多的应用开始使用API接口来提供服务。而API接口的测试也变得越来越重要。本文将介绍如何使用Python语言进行小红书笔记详情API接口的测试。 二、小红书笔记详情API接口介绍 小红书笔记详情API接口是用于获取指定笔记详细信息的接…...

实验六:Java流式编程与网络程序设计
一、字节输入/输出流实现数据的保存和读取 编程要求 根据提示,在右侧编辑器补充代码。 编写应用程序(SortArray.java),使用字节输入/输出流实现数据的保存和读取。 要求功能如下: 输入1~100之间的整型数据保存到数组…...

金字塔原理
金字塔原理 来自于麦肯锡公司的第一位女性咨询顾问芭芭拉•明托的著作《金字塔原理》。 原理介绍 此原理是一种重点突出、逻辑清晰、主次分明的逻辑思路、表达方式和规范动作。 金字塔的基本结构是:中心思想明确,结论先行,以上统下ÿ…...

VR全景技术助力政务服务大厅数字化,打造全新政务服务体验
引言: 随着科技的飞速发展,虚拟现实(VR)技术逐渐走进人们的视野。VR全景技术作为VR领域的一项重要应用,以其沉浸式、交互式的特点,正逐渐渗透到各行各业。政务服务大厅作为相关部门与民众之间的桥梁&#…...

使用Python实现SVM来解决二分类问题
下面是一个使用Python实现SVM来解决二分类问题的例子: # 导入所需的库 from sklearn.datasets import make_blobs from sklearn.model_selection import train_test_split from sklearn.svm import SVC import matplotlib.pyplot as plt# 生成一个二分类数据集 X, …...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

LabVIEW双光子成像系统技术
双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制,展现出显著的技术优势: 深层组织穿透能力:适用于活体组织深度成像 高分辨率观测性能:满足微观结构的精细研究需求 低光毒性特点:减少对样本的损伤…...
