C语言你爱我么?(ZZULIOJ 1205:你爱我么?)
题目描述
LCY买个n束花准备送给她暗恋的女生,但是他不知道这个女生是否喜欢他。这时候一个算命先生告诉他让他查花瓣数,第一个花瓣表示"爱",第二个花瓣表示"不爱",第三个花瓣表示"爱".....
为了使最后结果是"爱",LCY需要从n束花中选出一些,你能帮他算出最后他送给这个女生的花中最多包含多少个花瓣吗?
输入:
首先输入一个整数T,表示测试实例的个数。
接下来T组测试实例,每组实例首先输入一行,包括一个整数n(1 <= n <= 100)。
然后输入一行,n个数a1,a2...an(1 <= ai <= 100),表示每束花包含的花瓣的个数。
输出:
每组实例输出一个整数,表示LCY最多能送多少个花瓣给这个女生。
样例输入 Copy
3 1 1 1 2 3 5 6 7样例输出 Copy
1 0 13提示:每一束花不允许去掉一些花瓣再送。这样算命就不准了-_-#
思路:解决这个问题,理清两点即可,即所有的花瓣数量之和是奇数还是偶数的问题,
1.当所有花瓣数量之和为奇数时,则直接输出和即可。
2.当所有花瓣数量之和为偶数时,有两种情况,第一种情况所有的花束的花瓣数量都是偶数,这种情况输出0即可,第二种情况是部分花束的花瓣数量为奇数,部分为偶数,这种情况只需用所有花瓣数量之和减去花束中最小的的奇数花瓣数量即为最大花瓣数。
程序代码
#include<stdio.h>
int main(){int T;scanf("%d",&T);//输入一个整数T表示测试的案例数while(T--){int n;//输入一个整数n表示花束数量scanf("%d",&n);int a[n];//定义一个数组a用来存储每一束花的花瓣数int sum=0;int min=100;for(int i=0;i<n;i++){scanf("%d",&a[i]);//输入每束花的花瓣数sum+=a[i];if(a[i]%2!=0&&a[i]<min){//找到最小的奇数,并赋值给minmin=a[i];}}if(sum%2!=0) printf("%d\n",sum);//当所有花瓣之和为奇数时,输出sumelse if(min==100) printf("0\n");//当min的值不变,说明所有花的花瓣都为偶数,则输出0else printf("%d\n",sum-min);//当所有花瓣的和为偶数时,就减去最小的那个奇数,得到最大的奇数花瓣数}return 0;
}运行结果
相关文章:

C语言你爱我么?(ZZULIOJ 1205:你爱我么?)
题目描述 LCY买个n束花准备送给她暗恋的女生,但是他不知道这个女生是否喜欢他。这时候一个算命先生告诉他让他查花瓣数,第一个花瓣表示"爱",第二个花瓣表示"不爱",第三个花瓣表示"爱"..... 为了使最…...
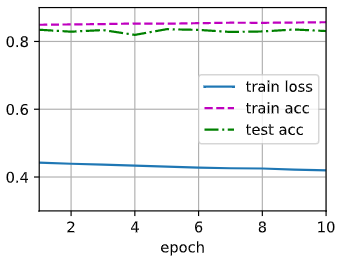
动手学深度学习(三)---Softmax回归
文章目录 一、理论知识1.图像分类数据集2.softmax回归的从零开始实现3.Softmax简洁实现 【相关总结】torch.sum()torch.argmax()isinstance():[python] softmax回归 一、理论知识 回归估计一个连续值分类预测一个离散类别 回归单连续数值输出自然区间R跟真实值的区别作为损失 …...

爬虫代理技术与构建本地代理池的实践
爬虫中代理的使用: 什么是代理 代理服务器 代理服务器的作用 就是用来转发请求和响应 在爬虫中为何需要使用代理? 隐藏真实IP地址:当进行爬取时,爬虫程序会发送大量的请求到目标网站。如果每个请求都使用相同的IP地址ÿ…...
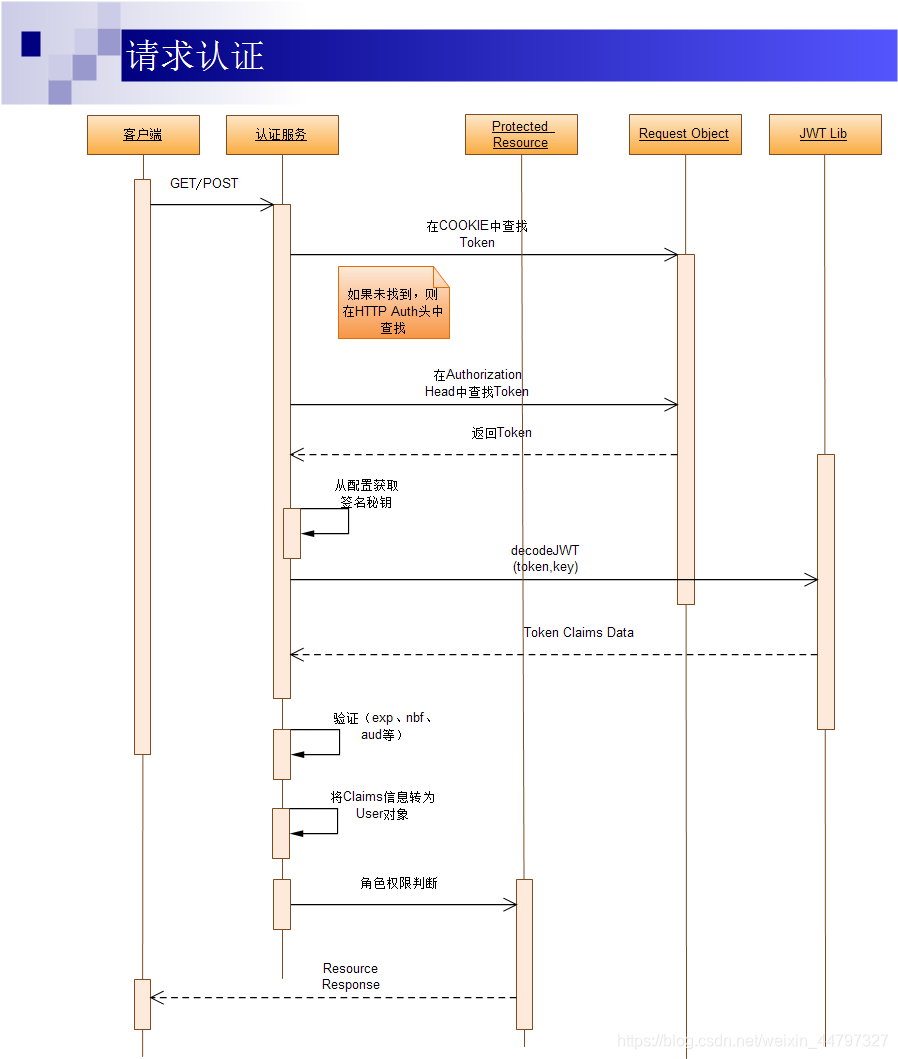
token认证机制,基于JWT的Token认证机制实现,安全性的问题
文章目录 token认证机制几种常用的认证机制HTTP Basic AuthOAuthCookie AuthToken AuthToken Auth的优点 基于JWT的Token认证机制实现JWT的组成认证过程登录请求认证 对Token认证的五点认识JWT的JAVA实现 基于JWT的Token认证的安全问题确保验证过程的安全性如何防范XSS Attacks…...

什么是计算机病毒?
计算机病毒 1. 定义2. 计算机病毒的特点3. 计算机病毒的常见类型和攻击方式4. 如何防御计算机病毒 1. 定义 计算机病毒是计算机程序编制者在计算机程序中插入的破坏计算机功能或者破坏数据,影响计算机使用并且能够自我复制的一组计算机指令或程序代码。因其特点与生…...
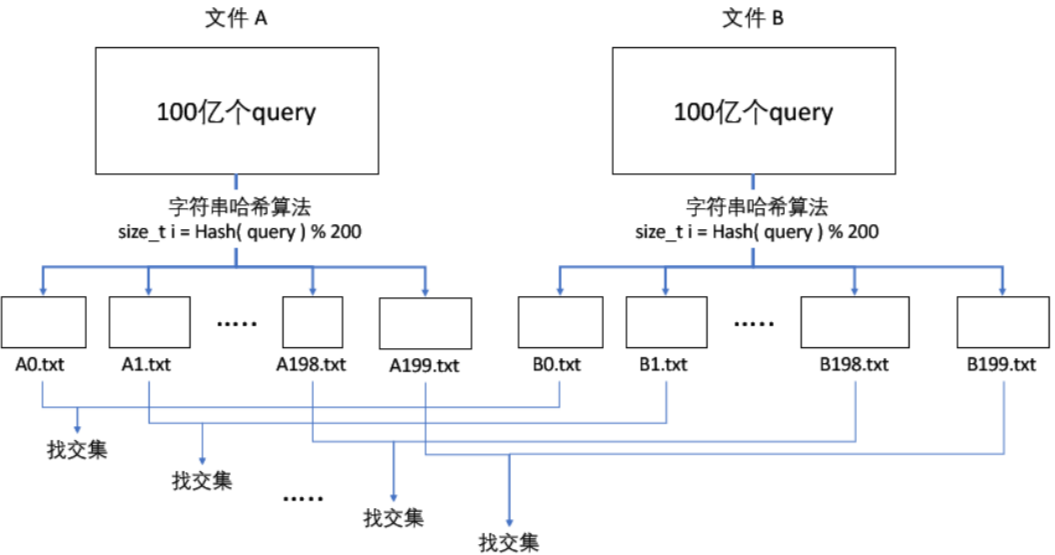
【C++】哈希(位图、布隆过滤器)
一、哈希的应用(位图和布隆过滤器) 1、位图(bitset) (1)位图概念 【题目】 给 40亿 个不重复的无符号整数,没排过序。给一个无符号整数,如何快速判断一个数是否在这 40亿 个数中。…...

LeetCode198.打家劫舍
打家劫舍和背包问题一样是一道非常经典的动态规划问题,只要做过几道动态规划的题,这道题简直就非常容易做出来。我应该花了10来分钟左右就写出来了,动态规划问题最重要的就是建立状态转移方程,就是说如何从上一个状态转移到下一个…...
Appium PO模式UI自动化测试框架——设计与实践
1. 目的 相信做过测试的同学都听说过自动化测试,而UI自动化无论何时对测试来说都是比较吸引人的存在。相较于接口自动化来说,它可以最大程度的模拟真实用户的日常操作与特定业务场景的模拟,那么存在即合理,自动化UI测试自然也是广…...
使用VUE3实现简单颜色盘,吸管组件,useEyeDropper和<input type=“color“ />的使用
1.使用vueuse中的useEyeDropper来实现滴管的功能和使用input中的type"color"属性来实现颜色盘 效果: 图标触发吸管 input触发颜色盘 组件代码部分 :<dropper> ---- vueuse使用 <template><div class"sRGBHexWrap fbc…...
)
matlab提取特征(医学图像)
乳腺肿瘤图片提取特征: %形态特征 %周长 面积 周长面积比 高度 宽度 纵横比 圆度 矩形度 伸长度 拟合椭圆长轴长 拟合椭圆短轴长 %拟合椭圆长轴与皮肤所夹锐角 最小外接凸多边形面积 最小外接凸多边形面积与肿瘤区面积比 %小叶树 叶指数 %纹理特征 %方差 熵 最小边差异 四个方…...
P4 C++ 条件与分支(if)
前言 今天我们来看看条件语句,换句话说,也就是 if 语句、if else 和 else if 等等这写语句。 我知道大家基本上已经非常了解 if 语句和所有 C 中的分支语句,但我还是鼓励你们继续看完这一讲,这里可能包含一些新东西。我们还会深入…...
django+drf+vue 简单系统搭建 (4) 用户权限
权限控制是web中的重要组成部分。与以往的博客系统不同,本次工具页面仅支持注册用户。 每个注册用户都能访问到工具页面,并且提交自己的task来选择具体的工具来处理自己提交的文件。每个注册用户都只能访问到自己提交的task,而管理员则可以查…...

stm32 计数模式
计数模式 但是对于通用定时器而言,计数器的计数模式不止向上计数这一种。上文基本定时器中计数器的计数模式都是向上计数的模式。 向上计数模式:计数器从0开始,向上自增,计到和自动重装寄存器的目标值相等时,计数器清…...
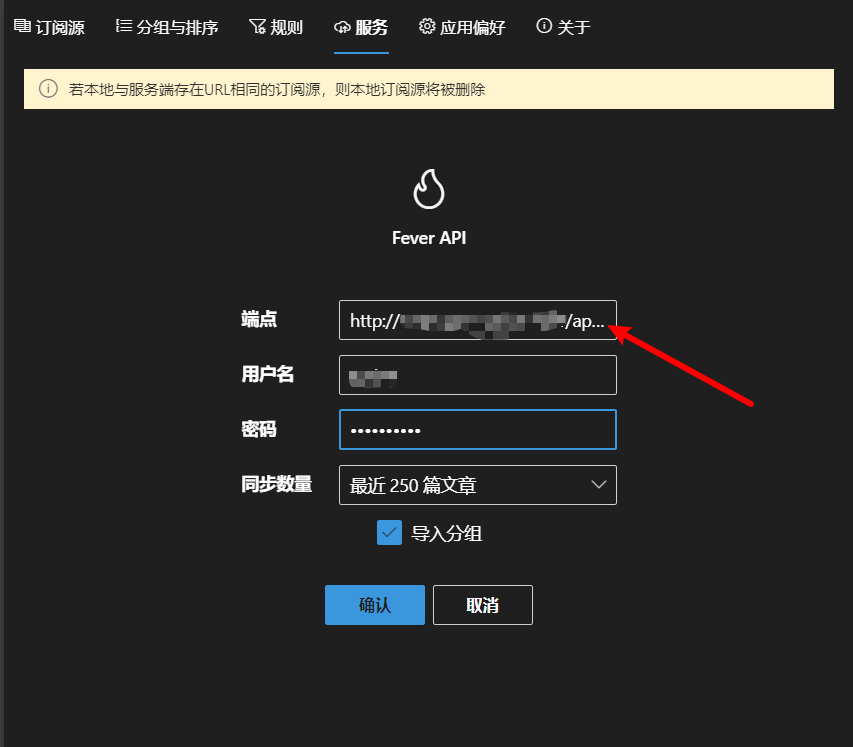
rss服务搭建记录
layout: post title: RSS subtitle: vps搭建RSS服务 date: 2023-11-27 author: Sprint#51264 header-img: img/post-bg-universe.jpg catalog: true tags: - 折腾 文章目录 引言RSShub-dockerRSS-radarFreshrssFluent reader获取fever api配置Fluent Reader同步 结语 引言 一个…...

GEE 23:基于GEE实现物种分布模型之随机森林法
基于GEE实现物种分布模型之随机森林法 1.物种分布数据2.研究区绘制3.预测因子选择 1.物种分布数据 根据研究目的和需要导入物种数据: // Load presence data var Data ee.FeatureCollection("users/************736/Distribution"); print(Original da…...
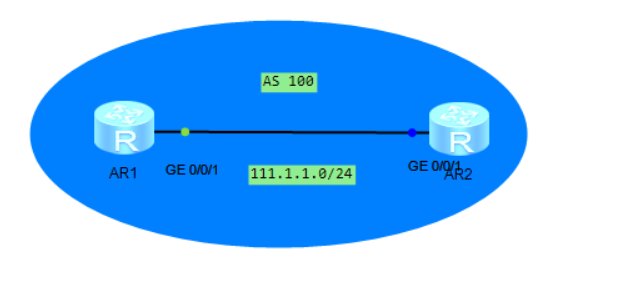
HCIE 01:基于前缀列表的BGP ORF功能
当运行BGP协议的某台设备上,针对入方向配置了基于ip-prefix的路由过滤,过滤了邻居发送的路由; 目前想,通过在peer关系的两端设备上都配置ORF功能,实现路由发送端只能送路由接收端过滤后的路由; ORF功能的说…...
基于SSM的云鑫曦科技办公自动化管理系统设计与实现
基于SSM的云鑫曦科技办公自动化管理系统设计与实现 摘 要: 随着时代的发展,单位办公方式逐渐从传统的线下纸张办公转向了使用个人pc的线上办公,办公效率低下的传统纸质化办公时代的淘汰,转型到信息化办公时代,面对当今数据逐渐膨…...

Angular项目中如何管理常量?
在Angular项目中,你可以使用不同的方式来管理常量。以下是一些常见的方法: 1、常量文件: 创建一个单独的 TypeScript 文件,其中包含你的常量。例如,创建一个名为 constants.ts 的文件,并在其中定义你的常量…...

【机器学习 | 可视化】回归可视化方案
🤵♂️ 个人主页: AI_magician 📡主页地址: 作者简介:CSDN内容合伙人,全栈领域优质创作者。 👨💻景愿:旨在于能和更多的热爱计算机的伙伴一起成长!!&…...

树与二叉树堆:链式二叉树的实现
目录 链式二叉树的实现: 前提须知: 前序: 中序: 后序: 链式二叉树的构建: 定义结构体: 初始化: 构建左右子树的指针指向: 前序遍历的实现: 中序…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

uniapp 字符包含的相关方法
在uniapp中,如果你想检查一个字符串是否包含另一个子字符串,你可以使用JavaScript中的includes()方法或者indexOf()方法。这两种方法都可以达到目的,但它们在处理方式和返回值上有所不同。 使用includes()方法 includes()方法用于判断一个字…...

关于uniapp展示PDF的解决方案
在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项: 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库: npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...

Unity中的transform.up
2025年6月8日,周日下午 在Unity中,transform.up是Transform组件的一个属性,表示游戏对象在世界空间中的“上”方向(Y轴正方向),且会随对象旋转动态变化。以下是关键点解析: 基本定义 transfor…...

ubuntu22.04有线网络无法连接,图标也没了
今天突然无法有线网络无法连接任何设备,并且图标都没了 错误案例 往上一顿搜索,试了很多博客都不行,比如 Ubuntu22.04右上角网络图标消失 最后解决的办法 下载网卡驱动,重新安装 操作步骤 查看自己网卡的型号 lspci | gre…...

2025年- H71-Lc179--39.组合总和(回溯,组合)--Java版
1.题目描述 2.思路 当前的元素可以重复使用。 (1)确定回溯算法函数的参数和返回值(一般是void类型) (2)因为是用递归实现的,所以我们要确定终止条件 (3)单层搜索逻辑 二…...
 ----- Python的类与对象)
Python学习(8) ----- Python的类与对象
Python 中的类(Class)与对象(Object)是面向对象编程(OOP)的核心。我们可以通过“类是模板,对象是实例”来理解它们的关系。 🧱 一句话理解: 类就像“图纸”,对…...

DeepSeek越强,Kimi越慌?
被DeepSeek吊打的Kimi,还有多少人在用? 去年,月之暗面创始人杨植麟别提有多风光了。90后清华学霸,国产大模型六小虎之一,手握十几亿美金的融资。旗下的AI助手Kimi烧钱如流水,单月光是投流就花费2个亿。 疯…...
