python 实现 AIGC 大语言模型中的概率论:生日相同问题的代码场景模拟
对深度学习本质而言,它实际上就是应用复杂的数学模型对输入数据进行建模,最后使用训练好的模型来预测或生成新的数据,因此深度学习的技术本质其实就是数学。随着大语言模型的发展,人工智能的数学本质被进一步封装,从业者要不直接调用给定模型处理给定数据,有点“技术内涵”的就是在给定模型基础上进行“微调”,我看现在很多 国内的AIGC 创业团队,几乎没有多少人有能力对开源的大模型进行修改或创造的能力。主要原因在于大模型的训练需要天量的数据和算力外,还在于其在数学理论基础上有很高的要求。我们很多人因此只能局限于AIGC 的“术”,也就是拿一个开源模型去适配特定的商业需求或场景,对于AIGC 的”道“而言,就只能讳莫如深,因为其要求的数学门槛太高。
从务虚的角度看, AIGC 内核中的数学思维极为精妙,我们若没有相应的能力去把握欣赏,那就相当于我们从未读过唐诗宋词,人生中失去了体会人类思维认知之美的机会。从务实的角度看,如果你只掌握”微调“能力,但没有能力在数学本质上看透大模型的算法本质,你很难利用大模型去适应或解决千变万化的商业场景和需求,因此只能生硬的”削足适履“,这也是我认为很多 AIGC 创业团队没有太多机会的原因。
当然要想磨练扎实的数学基础能力绝非易事。传统大学研究模式的数学学习方式太过于抽象和枯燥,我觉得数学学习就是被这种机械化,非人性化的学习方式搞坏。于是我就在想,我们能否通过工程化,代码化,具体化的方式来学习数学,于是就有了这里的尝试。我想实施能否通过代码的方式来探究掌握 AIGC 数学理论基础中的概率和数理统计部分,如果真有效果,后面我们也可以通过同样的方式来学习研究AIGC 的数学分析和高等代数部分,通过具体的实践方式来研究掌握抽象的思维理论。
我们首先着手的是概率论中经典的生日问题:一个房间中需要多少人才能使得其中某两个人出生在同一天的概率不少于 50%。处理数学问题的第一要点就是需要对问题进行没有歧义的,足够严谨和精准的描述,我们这里的描述其实就有很多模糊之处,因为它包含了很多没有说清楚的隐含假设。首先这个描述隐含的假设是房间内人与人之间的生日没有相互联系,但如果房间内的人都是双胞胎呢?双胞胎的生日显然不是互不关联的。因此我们对问题的描述就要增加一个前提,那就人与人的生日之间要相互独立,于是问题修改成:假设房间中每个人的生日都有可能在一年中的某一天,那么需要房间中有多少人,才能使得其中某两个人在同一天出生的概率不小于 50%。
修改后的问题描述足够清晰,足够严谨了吗?事实上问题的描述其实还隐含着一个假设,那就是房间中人与人之间没有特定联系。但如果某些原因让一些具有特定关系的人来到同一个屋子,并且这种特定关系影响到人生日的相互联系呢?杰拉德威尔在其著作《异类》中说过一个事情,加拿大青少年冰球联盟中每个级别选手按年龄分组,同年 1 月 1 日到 12 月 30 日出生的人都在同一组,这导致出生越靠近 1 月 1 日的选手竞争优势越大,因为他们年龄相对较大,身体的生长,营养的吸收,心理的稳定相对于靠近 12 月 30 日出生的选手更好,也就是”生理成熟度“更好,于是他们在训练中成绩更好,更容易放到”优秀组“里,于是更能得到优秀教练的指导,接收更有针对性的训练方案,于是他们成为职业选手的几率也就越大,于是如果进入屋子的是加拿大青年冰球职业球员,那么他们的生日就不再具有随机性。
由此我们还需要对问题的陈述做进一步改进:假设进入屋子的人,他们的生日日期相互独立,并且等可能的落入一年 365 天中的任何一天,那么我们需要屋子里有多少人,才能使得其中某两个人有相同生日的概率大于 50%.
在进行数学分析和推导前,我们先用代码模拟一下该问题,从感性上先对这个问题有初步认识:
import random
#记录当前生日分布情况
birthday_map = {}
#试验次数
try_times = 10000
experiences_times = try_times
total_count = 0
people_count = 0
while try_times > 0:#随机从 365 中选择一个数值模拟人的生日birth_day = random.randrange(1,365)if birth_day in birthday_map:#有人生日发生重复total_count += people_countbirthday_map = {}try_times -= 1people_count = 0else:#当前没有人生日发生重复people_count += 1birthday_map[birth_day] = 1print(f"people count for share birth day: {total_count / experiences_times}")上面代码使用随机数的方式来模拟人的生日,我们从[1,365]这个范围内随机抽取一个数作为人的生日,如果当前抽取的数值在前面出现过,那意味着两个人的生日出现了重复,我们把模拟试验设置成 10000 次,然后记录每次试验出现重复随机数时的计数,把 10000 次试验的计数加总再求平均就能模拟出一群人出现重复生日所需人数,上面代码运行后所得结果:
people count for share birth day: 23.323
你可以尝试多次就可以发现,几乎每次试验结果都是 23 左右,这意味着问题的答案可能就是 23,后面我们通过严谨的数学推导看看为何 23 就是答案。更多内容请在 B 站搜索 coding 迪斯尼。
相关文章:

python 实现 AIGC 大语言模型中的概率论:生日相同问题的代码场景模拟
对深度学习本质而言,它实际上就是应用复杂的数学模型对输入数据进行建模,最后使用训练好的模型来预测或生成新的数据,因此深度学习的技术本质其实就是数学。随着大语言模型的发展,人工智能的数学本质被进一步封装,从业…...
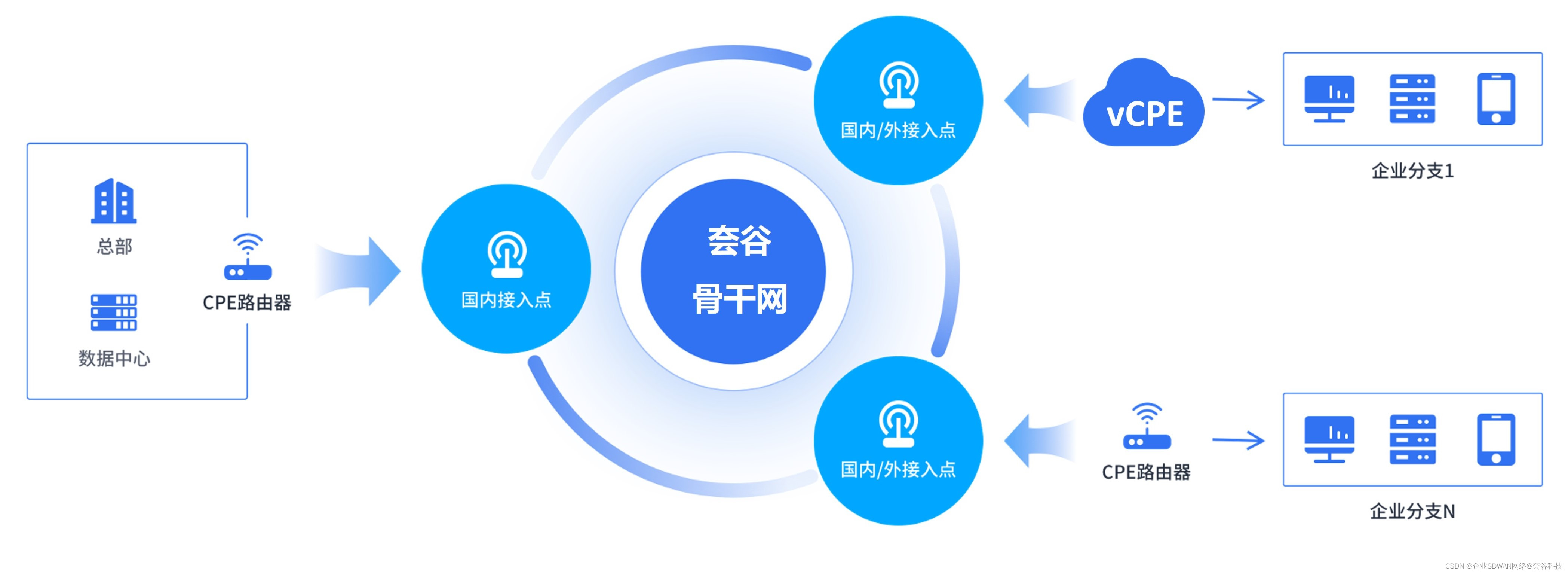
SD-WAN组网中的CPE及云服务CPE部署方法
什么是CPE? CPE全称为Customer Premises Equipment,即客户端设备,在SD-WAN中通常为路由器,部署在中心点和分支上,提供连接和路由、协议转换、流量监控等功能。一般可分为硬件CPE和虚拟化CPE(virtual CPE&a…...
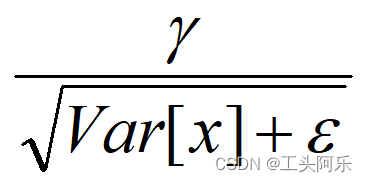
理解BatchNormalization层的作用
深度学习 文章目录 深度学习前言一、“Internal Covariate Shift”问题二、BatchNorm的本质思想三、训练阶段如何做BatchNorm四、BatchNorm的推理(Inference)过程五、BatchNorm的好处六、机器学习中mini-batch和batch有什么区别 前言 Batch Normalization作为最近一年来DL的重…...
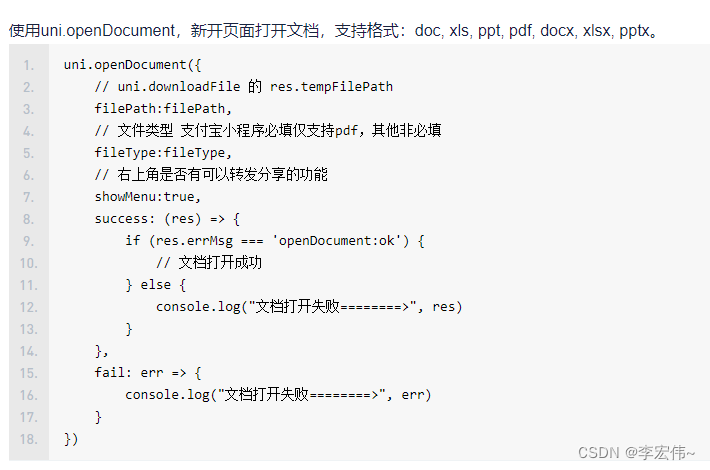
uniapp实现文件预览过程
H5实现预览 <template><iframe :src"_url" style"width:100vw; height: 100vh;" frameborder"0"></iframe> </template> <script lang"ts"> export default {data() {return {_url: ,}},onLoad(option…...

深度学习-学习笔记记录
1、点云语义分割方法分类 分为5类:点、二维投影、体素、融合、集成 2、融合与集成的区别 融合: 概念:主要是将不同来源、类型的模型,例如深度学习、传统机器学习等,的结果或特征进行结合,以得到一个更好的模…...

程序员养生之道:延寿不忘初心——延寿必备
文章目录 每日一句正能量前言如何养生饮食篇运动篇休息篇后记 每日一句正能量 现代社会已不是大鱼吃小鱼的年代,而是快鱼吃慢鱼的年代。 前言 在IT行业中,程序员是一个重要的职业群体。由于长时间的繁重编程工作,程序员们常常忽略了身体健康…...
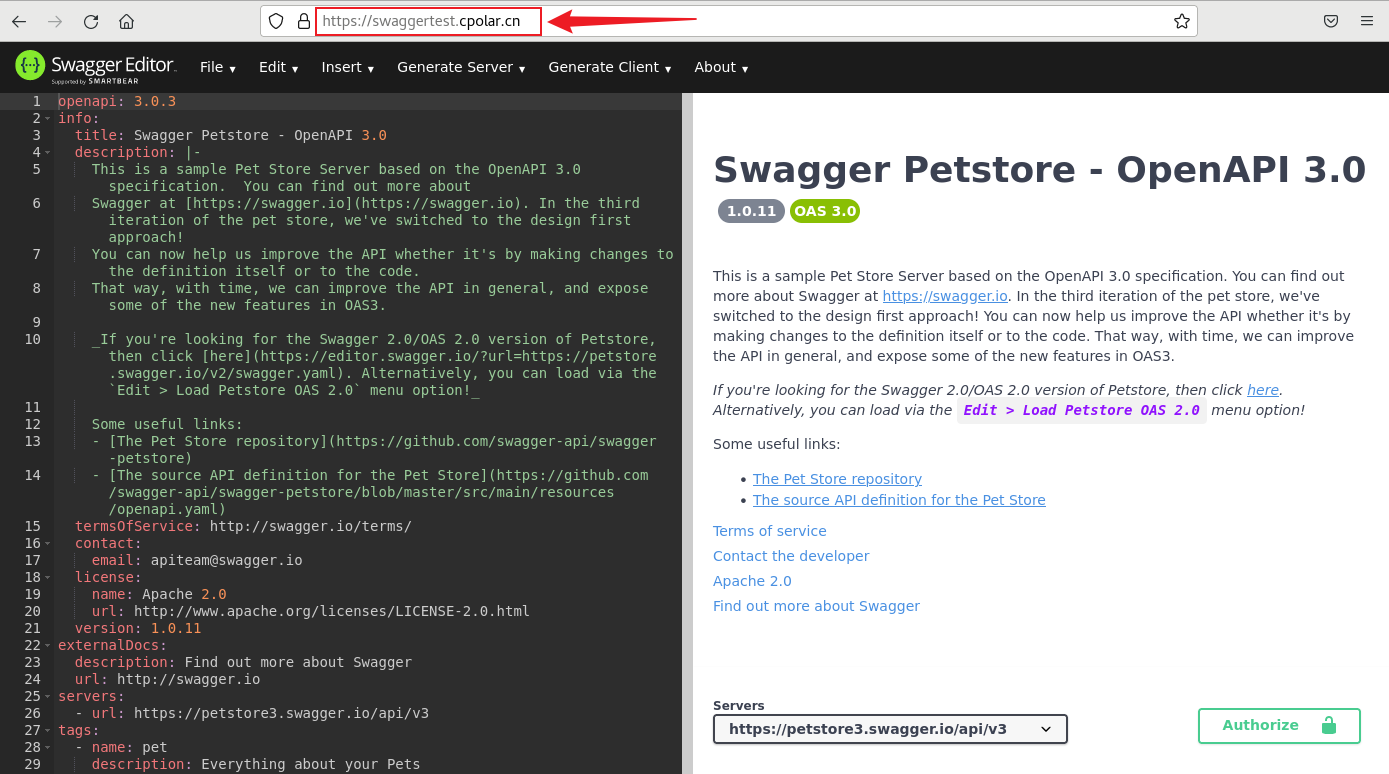
使用Docker安装部署Swagger Editor并远程访问编辑API文档
文章目录 Swagger Editor本地接口文档公网远程访问1. 部署Swagger Editor2. Linux安装Cpolar3. 配置Swagger Editor公网地址4. 远程访问Swagger Editor5. 固定Swagger Editor公网地址 Swagger Editor本地接口文档公网远程访问 Swagger Editor是一个用于编写OpenAPI规范的开源编…...
Nacos 2.X核心架构源码剖析
概述 注册中心并发处理,1.4.x 写时复制,2.1.0 读写分离;nacos 一般使用 AP 架构,即临时实例,1.4.x 为 http 请求,2.1.0 优化为 gRPC 协议;源码中使用了大量的事件通知机制和异步定时线程池&…...
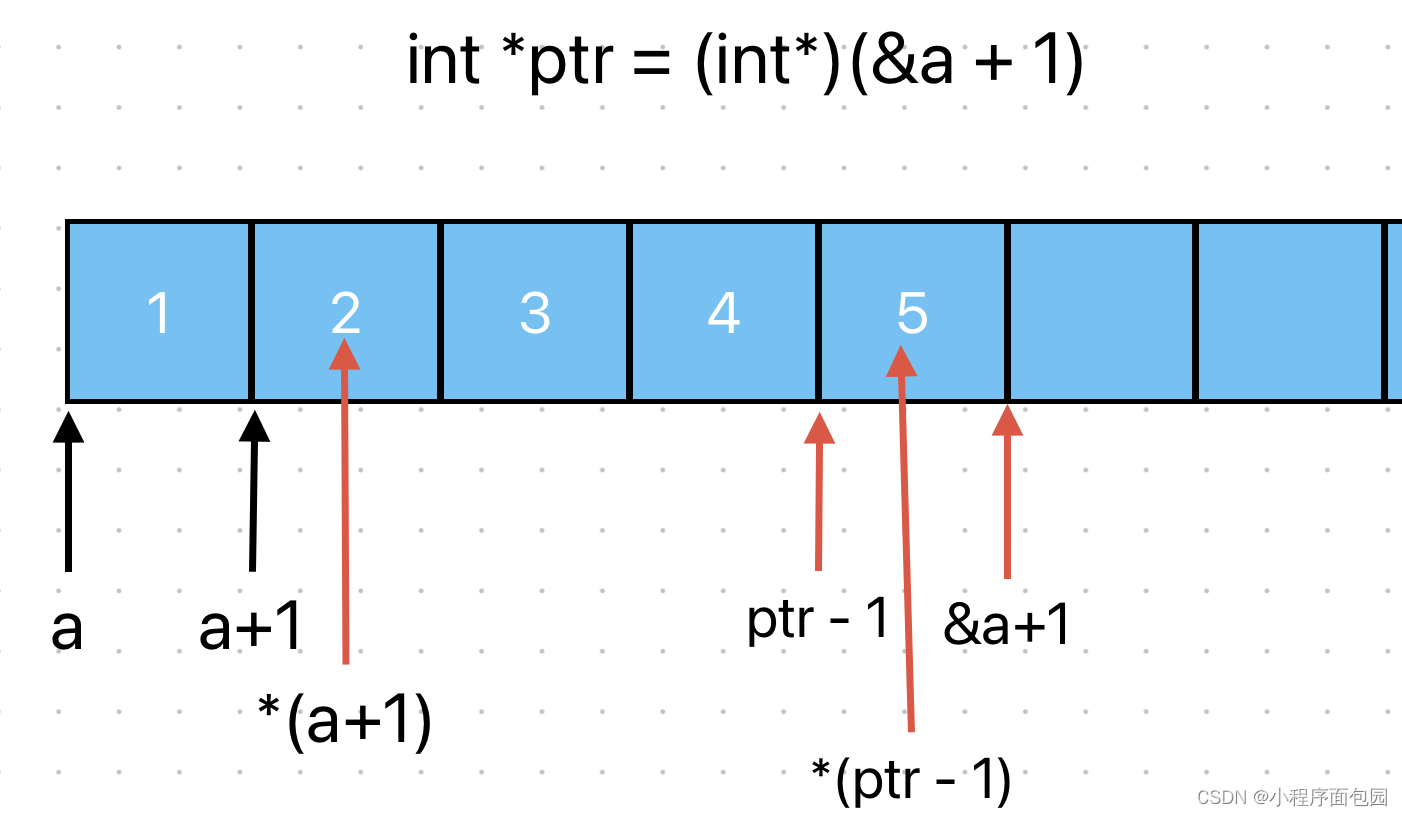
C语言--每日选择题--Day31
第一题 1. 下面程序 i 的值为() int main() {int i 10;int j 0;if (j 0)i; elsei--; return 0; } A:11 B:9 答案及解析 B if语句中的条件判断为赋值语句的时候,因为赋值语句的返回值是右操作数; …...

chrome vue devTools安装
安装好后如下图所示: 一:下载vue devTools 下载链接https://download.csdn.net/download/weixin_44659458/13192207?spm1001.2101.3001.6661.1&utm_mediumdistribute.pc_relevant_t0.none-task-download-2%7Edefault%7ECTRLIST%7EPaid-1-13192207…...

Spring Security 6.x 系列(7)—— 源码分析之Builder设计模式
一、Builder设计模式 WebSecurity、HttpSecurity、AuthenticationManagerBuilder 都是框架中的构建者,把他们放到一起看看他们的共同特点: 查看AuthenticationManagerBuilder的继承结构图: 查看HttpSecurity的继承结构图: 查看W…...

PyQt6 中自定义浮点型滑块类
介绍: 在PyQt6中,滑块(Slider)是常用的用户界面元素之一,用于选择数值范围。然而,有时候我们可能需要使用浮点数值,而标准的滑块仅支持整数。为了解决这个问题,我们可以创建一个自定…...

笔记,B+树
B树面对的场景,是一个有10亿行的表,希望某一列是有序的。这么大的数据量,内存里放不下,需要放在硬盘里。结果,原本运行于内存的二叉树,就升级为B树了。 在二叉树中,每个节点存储着一个数字&…...
代码随想录刷题题Day2
刷题的第二天,希望自己能够不断坚持下去,迎来蜕变。😀😀😀 刷题语言:C / Python Day2 任务 977.有序数组的平方 209.长度最小的子数组 59.螺旋矩阵 II 1 有序数组的平方(重点:双指针…...

【JAVA面向对象编程】--- 探索子类如何继承父类
🌈个人主页: Aileen_0v0🔥学习专栏: Java学习系列专栏 💫个人格言:"没有罗马,那就自己创造罗马~" 目录 继承 继承的普通成员方法调用 及 普通成员变量修改 构造方法的调用 子类构造方法 继承 package Inherit;class Animal …...

从浏览器控制台发送get,post请求
---------------------get请求--------------------------- fetch(url, { method: get, }) .then(response > response.json()) .then(data > { // 获取到响应的数据后的处理逻辑 console.log(data); }) .catch(error > { // 请求发生错误的处理逻…...
海外问卷调查怎么批量做?可以用指纹浏览器吗?
海外问卷调查通常是指产品与品牌上线时,基于消费者、市场调查而组织的问卷调查,包括个人、企业或其他组织,以获取关于市场、消费者行为、产品需求、社会趋势等方面的见解。 通常,研究人员或组织会设计一份问卷,通过在线…...

HarmonyOS 位置服务开发指南
位置服务开发概述 移动终端设备已经深入人们日常生活的方方面面,如查看所在城市的天气、新闻轶事、出行打车、旅行导航、运动记录。这些习以为常的活动,都离不开定位用户终端设备的位置。 当用户处于这些丰富的使用场景中时,系统的位置能力…...

ThinkPHP6学生选课管理系统
有需要请加文章底部Q哦 可远程调试 ThinkPHP6学生选课管理系统 一 介绍 此学生选课管理系统基于ThinkPHP6框架开发,数据库mysql8,前端bootstrap。系统角色分为学生,教师和管理员。学生登录后可进行选课,教师登录后可查看选课情况…...

uniapp如何与原生应用进行混合开发?
目录 前言 1.集成Uniapp 2.与原生应用进行通信 3.实现原生功能 4.使用原生UI组件 结论: 前言 随着移动应用市场的不断发展,使用原生开发的应用已经不能满足用户的需求,而混合开发成为了越来越流行的选择。其中,Uniapp作为一种跨平台的开…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...
