当前位置： 首页 > news >正文

【图论】重庆大学图论与应用课程期末复习资料2-各章考点（填空证明部分）（私人复习资料）

news 文章来源：https://blog.csdn.net/qq_25601345/article/details/134725766 2025/5/14 9:34:27

图论各章考点

  • 一、图与网络的基本概念
  • 二、树
  • 三、连通性
  • 四、路径算法
  • 五、匹配
  • 六、行遍性问题
  • 七、平面图

一、图与网络的基本概念

  1. 生成子图：生成子图 G ’ G’ G’中顶点个数V’必须和原图G中V的数量相同，而 E ’ ∈ E E’∈E E’∈E即可。
  2. 顶点集导出子图： V 1 ⊆ V V1⊆V V1⊆V，以 V 1 V1 V1为顶点集，两个端点都在 V V V中的边为边集的 G G G的子图。
  3. 边集导出子图： E 1 ⊆ E E1⊆E E1⊆E，以 E 1 E1 E1为边集， E 1 E1 E1的端点集为顶点集的图 G G G的子图。
  4. 简单图：既无环又无重边的图为简单图
  5. 完备图：任二顶点相邻的简单图,称为完备图,记为 K n K_n Kn​其中n 为顶点的数目
  6. 二部图：一个图是偶图（二部图）当且当它不包含奇圈
  7. 握手定理：图 G = ( V , E ) G= (V, E) G=(V,E)中所有顶点的度的和等于边数m的2倍
  8. 同构：顶点集之间存在一一对应关系，边也有一一对应的关系,则称图 G G G与 H H H同构，有向图的同构对应边的方向要相同。必要条件 (1) 顶点数相同(2) 边数相同(3) 关联边数相同的顶点个数相同。

二、树

  1. 树：无圈连通图称为树
  2. 树充要条件： G G G无环且任何两个顶点之间有唯一的路径
  3. 树充要条件： G G G连通,且 e ( G ) = V ( G ) − 1 e(G)=V(G)-1 e(G)=V(G)−1
  4. 树充要条件： G G G连通，且对 G G G的任一边 e , G − e e,G-e e,G−e不连通
  5. 生成树： G G G的边数最少的连通生成子图

三、连通性

  1. 点连通度：设 G G G连通, V ⊂ V ( G ) , G [ V − V ] V⊂V(G), G[V-V] V⊂V(G),G[V−V]不连通,则称 V V V为 G G G的点断集。最小点断集中顶点的个数称为 G G G的连通度记为 K ( G ) K(G) K(G)，若 G G G无点断集,则规定 K ( G ) = n − 1 K(G)=n-1 K(G)=n−1， 平凡图、不连通图 = 0 平凡图、不连通图=0 平凡图、不连通图=0
  2. 边连通度：设 G G G连通, E ⊂ E ( G ) E⊂E(G) E⊂E(G), G − E G-E G−E(从 G G G中删除 E E E中的边)不连通,则称 E E E是 G G G的边断集。最小边断集所含的边数称为 G G G的边连通度记为 K ‘ ( G ) K‘(G) K‘(G)，当 ∣ E ′ ∣ = 1 |E'|=1 ∣E′∣=1时,称E中的边 e e e为割边， 平凡图、不连通图 = 0 平凡图、不连通图=0 平凡图、不连通图=0
  3. k连通图：若一个图的连通度至少为 k k k，则称该图是 k k k连通的。于是，非平凡连通图均是 1 1 1连通的；图 G G G是2连通的当且仅当 G G G连通、无割点且至少含有 3 3 3个点。
  4. 点连通度、边连通度、最小度： K ( G ) < = K ′ ( G ) < = δ （ G ） K(G)<=K'(G)<=δ（G） K(G)<=K′(G)<=δ（G）
  5. 割边：设e是图G的一条边，若 ω ( G − e ) ＞ ω ( G ) ω(G-e)＞ω(G) ω(G−e)＞ω(G), 则称 e e e为 G G G的割边。 e e e是图 G G G的割边，当且仅当 e e e不在 G G G的任何圈中。
  6. 割点： v v v是 G G G的割点当且仅当 V ( G − v ) V(G-v) V(G−v)可划分为两个非空顶点子集 V 1 V_1 V1​与 V 2 V_2 V2​，使 x ∈ V 1 ， y ∈ V 2 x∈V_1，y∈V_2 x∈V1​，y∈V2​，点v都在每一条 ( x , y ) (x, y) (x,y) 路上。
  7. 割集： [ S , S ′ ] [S, S'] [S,S′]表示一个端点在 S S S,另一个端点在 S S S的全体边组成的集合，设 G G G连通,若 [ S , S ’ ] [S,S’] [S,S’]只把 G G G断成两个分支,则称 [ S , S ′ ] [S, S'] [S,S′]为 G G G的一个割集。
  8. 树和图：设 v v v是树的顶点，则 v v v是 G G G的割点当且仅当度 d ( v ) > = 2 d(v)>=2 d(v)>=2

习题15：去掉 e = ( u , v ) e= (u, v) e=(u,v) ，在 G − e G-e G−e中 u u u所在的分支仅有一个奇度顶点，与握手定理矛盾

习题16：反证法， e = ( u , v ) e= (u, v) e=(u,v) ， G − e G-e G−e中 u u u所在的分支 G 1 G_1 G1​， G 1 G_1 G1​为二部图，因为二部图所有子图均为二部图，则 Σ （ G 1 ） = k ∣ X 1 ∣ = k ∣ Y 1 ∣ − 1 = > k Σ（G_1）=k|X_1|=k|Y_1|-1=>k Σ（G1​）=k∣X1​∣=k∣Y1​∣−1=>k， （ ∣ X 1 ∣ − ∣ Y 1 ∣ ） = 1 （ k > = 2 ） （|X_1|-|Y_1|）=1（k>=2） （∣X1​∣−∣Y1​∣）=1（k>=2），不成立

四、路径算法

  1. Floyd：复杂度 O （ n 3 ） O（n^3） O（n3）

五、匹配

  1. 边独立集（匹配）：如果 M M M是图 G G G的边子集(不含环），且 M M M中的任意两条边没有共同顶点，则称 M M M是 G G G的一个匹配
  2. 最大匹配：如果 M M M是图 G G G的包含边数最多的匹配，称 M M M是 G G G的一个最大匹配。特别是，若最大匹配饱和了 G G G的所有顶点，称它为 G G G的一个完美匹配（理想匹配）
  3. 二部图理想匹配：若 G G G是 k ( k > 0 ) k (k>0) k(k>0)正则偶图，则 G G G存在完美匹配
  4. 贝尔热定理： G G G的匹配 M M M是最大匹配，当且仅当 G G G不包含M可扩路
  5. Hall定理：二分图存在完美匹配当且仅当 ∀ S ⊆ A \forall S\subseteq A ∀S⊆A，都有 ∣ N ( S ) ∣ ⩾ ∣ S ∣ |N(S)|\geqslant |S| ∣N(S)∣⩾∣S∣
  6. 哥尼定理：在偶图中，最大匹配的边数等于最小覆盖的顶点数
  7. 托特定理：图 G G G有完美匹配当且仅当对V的任意非空真子集S, 有： （奇分支数目 ) ∣ o ( G − S ) ∣ ⩽ ∣ S ∣ （奇分支数目)|o(G-S)|\leqslant |S| （奇分支数目)∣o(G−S)∣⩽∣S∣

六、行遍性问题

  1. 欧拉巡回：经过 G G G的每边正好一次的巡回称为欧拉巡回
  2. 欧拉图：存在欧拉巡回的图称为欧拉图或E图
  3. 欧拉图的充要条件：连通、无奇度顶点
  4. 欧拉道路的充要条件：连通、最多只有两个奇度顶点
  5. 哈米尔顿路径：经过图 G G G每个顶点正好一次的路径，简称 H H H路径。
  6. 哈米尔顿图：经过 G G G的每个顶点正好一次的圈为H圈。含H圈的图称为哈米尔顿图或 H H H图。
  7. H图的必要条件： 其 ∀ S ⊂ V ， S ≠ ∅ ω ( G − S ) ≤ ∣ S ∣ 其 \forall S \subset V ，S \neq \varnothing \\ \omega ( G - S ) \leq | S | 其∀S⊂V，S=∅ω(G−S)≤∣S∣

七、平面图

  1. 平面图：一个图若能在曲面 S S S上画出,使任两边在非顶点处不相交,则称此图可以在曲面 S S S上嵌人。可嵌入平面的图称为可嵌平面图,否则称为非平面图。可嵌平面图 G G G嵌人平面形成的图,称为 G G G的平面嵌入。
  2. 欧拉公式：设 G = ( n , m ) G=(n, m) G=(n,m)是连通平面图， ϕ \phi ϕ是G的面数， n − m + ϕ = 2 n - m + \phi = 2 n−m+ϕ=2
  3. 平面图推论： G G G是 v > = 3 v>=3 v>=3的简单平面图， ε ≤ 3 v − 6 \varepsilon \leq 3 v - 6 ε≤3v−6， δ ( G ) ≤ 5 \delta ( G ) \leq 5 δ(G)≤5
  4. 库拉托夫斯基定理：图 G G G是非可平面的，当且仅当它含有 K 5 K_5 K5​或 K 3 , 3 K_{3,3} K3,3​细分的子图

相关文章：

【图论】重庆大学图论与应用课程期末复习资料2-各章考点（填空证明部分）（私人复习资料）

图论各章考点 一、图与网络的基本概念二、树三、连通性四、路径算法五、匹配六、行遍性问题七、平面图 一、图与网络的基本概念 生成子图&#xff1a;生成子图 G ’ G’ G’中顶点个数V’必须和原图G中V的数量相同&#xff0c;而 E ’ ∈ E E’∈E E’∈E即可。顶点集导出子图…...

编程日记 2023/12/2 10:11:07

基于Intel® AI Analytics Toolkits的智能视频监控系统

【oneAPI DevSummit & OpenVINODevCon联合黑客松】 跳转链接&#xff1a;https://marketing.csdn.net/p/d2322260c8d99ae24795f727e70e4d3d 目录 1方案背景 2方案描述 3需求分析 4技术可行性分析 5详细设计5.1数据采集 5.2视频解码与帧提取 5.3人脸检测 5.4行为识别…...

编程日记 2023/12/2 10:10:06

深度学习中的注意力机制：原理、应用与实践

深度学习中的注意力机制&#xff1a;原理、应用与实践 摘要&#xff1a; 本文将深入探讨深度学习中的注意力机制&#xff0c;包括其原理、应用领域和实践方法。我们将通过详细的解析和代码示例&#xff0c;帮助读者更好地理解和应用注意力机制&#xff0c;从而提升深度学习模…...

编程日记 2023/12/2 10:08:05

将本地项目推送到github

欢迎大家到我的博客浏览。将本地项目推送到github | YinKais Blog 本地项目上传至 GitHub<!--more--> 1、进入项目根目录&#xff0c;初始化本地仓库 git init 2、创建密钥&#xff1a;创建 .ssh 文件夹&#xff0c;并进入 .ssh 文件夹 mkdir .ssh cd .ssh/ 3、生成…...

编程日记 2023/12/2 10:05:01

[读论文]meshGPT

概述 任务&#xff1a;无条件生成mesh &#xff08;无颜色&#xff09;数据集&#xff1a;shapenet v2方法&#xff1a;先trian一个auto encoder&#xff0c;用来获得code book&#xff1b;然后trian一个自回归的transformermesh表达&#xff1a;face序列。face按规定的顺序&a…...

编程日记 2023/12/2 10:02:59

反序列化漏洞详解（一）

目录 一、php面向对象 二、类 2.1 类的定义 2.2 类的修饰符介绍 三、序列化 3.1 序列化的作用 3.2 序列化之后的表达方式/格式 ① 简单序列化 ② 数组序列化 ③ 对象序列化 ④ 私有修饰符序列化 ⑤ 保护修饰符序列化 ⑥ 成员属性调用对象 序列化 四、反序列化 …...

编程日记 2023/12/2 10:00:57

键盘打字盲打练习系列之指法练习——2

一.欢迎来到我的酒馆 盲打&#xff0c;指法练习&#xff01; 目录 一.欢迎来到我的酒馆二.开始练习 二.开始练习 前面一个章节简单地介绍了基准键位、字母键位和数字符号键位指法&#xff0c;在这个章节详细介绍指法。有了前面的章节的基础练习&#xff0c;相信大家对盲打也有了…...

编程日记 2023/12/2 9:57:54

小程序----使用图表显示数据--canvas

需求&#xff1a;在小程序上实现数据可视化 思路&#xff1a;本来想用的是echarts或者相关的可视化插件&#xff0c;但因为用的是vue3&#xff0c;大多数插件不支持&#xff0c;所以用了echarts&#xff0c;但最后打包的时候说包太大超过2M无法上传&#xff0c;百度了一下&…...

编程日记 2023/12/2 9:56:53

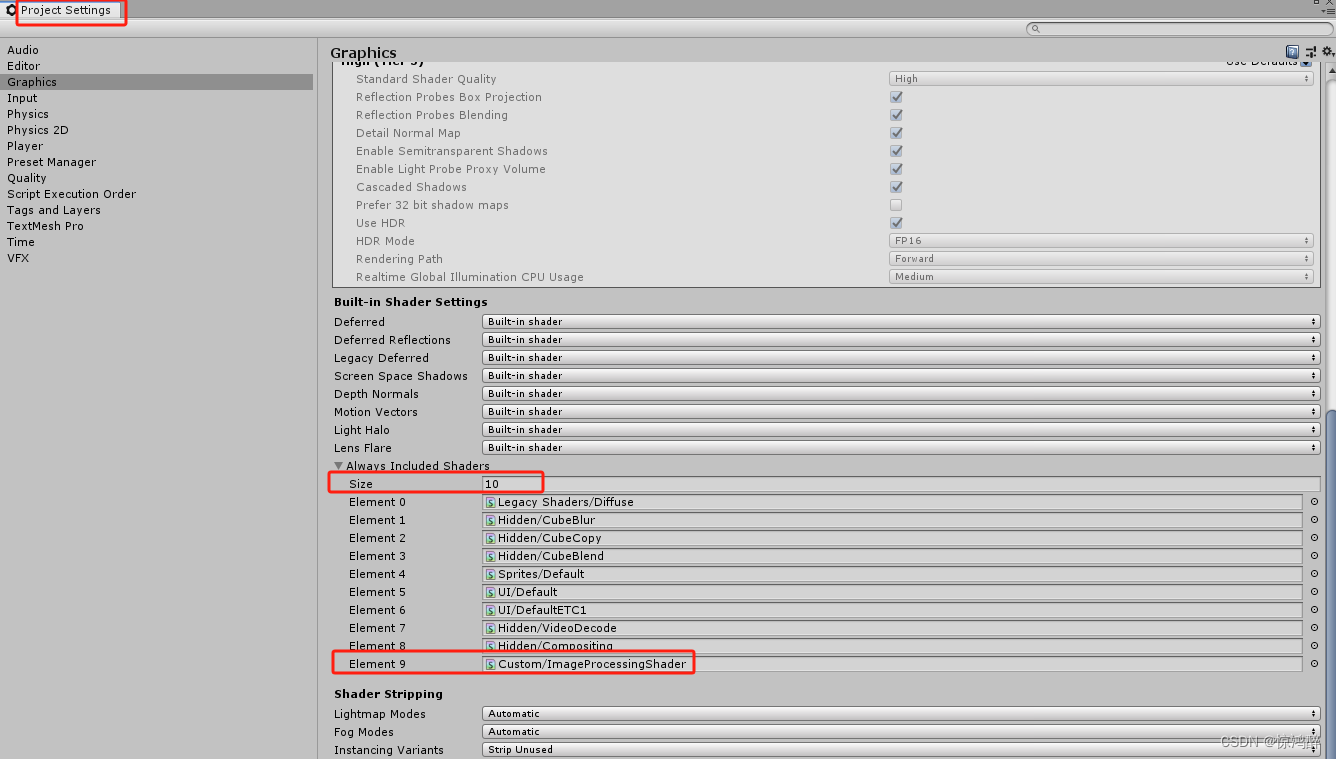
⭐ Unity 开发bug —— 打包后shader失效或者bug (我这里用Shader做两张图片的合并发现了问题)

1.这里我代码没啥问题~~~编辑器里也没毛病 void Start(){// 加载底图和上层图片string backgroundImagePath Application.streamingAssetsPath "/background.jpg";Texture2D backgroundTexture new Texture2D(2, 2);byte[] backgroundImageData System.IO.File.R…...

编程日记 2023/12/2 9:55:51

document

原贴连接 1.在整个文档范围内查询元素节点 功能API返回值根据id值查询document.getElementById(“id值”)一个具体的元素节根据标签名查询document.getElementsByTagName(“标签名”)元素节点数组根据name属性值查询document.getElementsByName(“name值”)元素节点数组根据类…...

编程日记 2023/12/2 9:54:50

NodeJS（二）：npm包管理工具、yarn、npx、pnpm工具等

目录 (一)npm包管理工具 1.了解npm 2.npm的配置文件 常见的配置属性 scripts属性*** 依赖的版本管理 3.npm安装包的细节 4.package-lock文件 5.npm install原理** 6.npm的其他命令 (二) 其他包管理工具 1.yarn工具 基本指令 2.cnpm工具 3.npx工具 (1)执行本地…...

编程日记 2023/12/2 9:53:49

day3 移出链表中值为x的节点

ListNode* removeElements(ListNode* head, int val) { ListNode* dummyHead new ListNode(0); // 设置一个虚拟头结点 dummyHead->next head; // 将虚拟头结点指向head&#xff0c;这样方便后面做删除操作 ListNode* cur dummyHead; while (cur->next ! NULL…...

编程日记 2023/12/2 9:51:47

浅谈 Guava 中的 ImmutableMap.of 方法的坑

作者&#xff1a;明明如月学长&#xff0c; CSDN 博客专家&#xff0c;大厂高级 Java 工程师&#xff0c;《性能优化方法论》作者、《解锁大厂思维&#xff1a;剖析《阿里巴巴Java开发手册》》、《再学经典&#xff1a;《EffectiveJava》独家解析》专栏作者。 热门文章推荐&…...

编程日记 2023/12/2 9:48:44

Symbol()和迭代器生成器

目录 1、Symbol&#xff08;&#xff09; 2、迭代器生成器 执行流程 模拟生成器函数 for of 遍历迭代选择器 yield * Generator函数应用 1、Symbol&#xff08;&#xff09; Symbol表示独一无二的值 const s1 Symbol(a)const s2 Symbol(a)console.log(s1 s2) // fa…...

编程日记 2023/12/2 9:47:43

USB Type-C的基本原理

1 USB Type-C的基本原理 1.1 基本特性 Figure 1-1 USB Type-C接头外形 USB Type-C&#xff08;简称USB-C&#xff09;的基本特性&#xff1a; 1. 接口插座的尺寸与原来的Micro-USB规格一样小&#xff0c;约为8.3mm X 2.5mm 2. 可承受1万次反复插拔 3. 支持正反均可插入的“正反…...

编程日记 2023/12/2 9:45:42

HarmonyOS开发(八)：动画及网络

1、动画概述 在ArkUI中&#xff0c;产生动画的方式是改变组件属性值并且指定相关的动画参数。当属性值发生变化后&#xff0c;按照动画参数&#xff0c;从原来的状态过渡到新的状态&#xff0c;就形成一个动画。 动画的相关参数如下&#xff1a; 属性名称 属性类型 默认值 …...

编程日记 2023/12/2 9:43:40

Pinctrl子系统和GPIO子系统

Pinctrl子系统&#xff1a; 借助Princtr子系统来设置一个Pin的复用和电气属性&#xff1b; pinctrl子系统主要做的工作是&#xff1a;1. 获取设备树中的PIN信息&#xff1b;2.根据获取到的pin信息来设置的Pin的复用功能&#xff1b;3.根据获取到的pin信息去设置pin的电气特性…...

编程日记 2023/12/2 9:42:39

Unittest单元测试框架之unittest构建测试套件

构建测试套件 在实际项目中&#xff0c;随着项目进度的开展&#xff0c;测试类会越来越多&#xff0c;可是直到现在我 们还只会一个一个的单独运行测试类&#xff0c;这在实际项目实践中肯定是不可行的&#xff0c;在 unittest中可以通过测试套件来解决该问题。 测试套件&…...

编程日记 2023/12/2 9:41:38

Django回顾4

一.过滤器 1.过滤器格式 {{变量|过滤器名字}} 2.怎么使用 1.注册app 2.在app下创建templatetags模块&#xff08;模块名只能是templatetags&#xff09; 3.在包下写一个py文件&#xff0c;随便命名 4.在py文件中写入&#xff1a;from django import template …...

编程日记 2023/12/2 9:40:37

Apache APISIX 体验指南

APISIX 体验指南 所有的 sh 脚本通过 git bash 执行。 出现错误仔细核对文档。 github 地址&#xff1a; 使用 docker 安装 apisix 确保本地安装 Docker 和 Docker-compose 如未安装参开以下文档安装&#xff1a; Docker&#xff1a;https://docs.docker.com/engine/install/c…...

编程日记 2023/12/2 9:36:32

Promise的resolve和reject方法（手写题）

1.resolve 2.reject 3.手写 1.resolve //构造函数上添加 resolve 方法 Promise.resolve function (value) {return new Promise((resolve, reject) > {if (value instanceof Promise) {value.then((val) > {resolve(val)},(err) > {reject(err)})} else {resolve(v…...

编程日记 2023/12/2 9:35:31

关于wiki的Unlink攻击理解--附例题BUUCTF-hitcontraining_bamboobox1

堆机制我研究了很久&#xff0c;一直没有什么很大的进展。堆相较于栈难度大的多。利用手法也多。目前还没有怎么做过堆题。这次就把理解了很久的Unlink写一写。然后找一题实践一下。 在glibc中&#xff0c;堆管理都是用一个个chunk去组织的。这个就不过多阐述。Unlink是glibc一…...

编程日记 2023/12/2 9:34:30

【linux】日志有哪些

Linux系统日志主要有以下几种类型&#xff1a; 内核及系统日志&#xff1a;这种日志数据由系统服务rsyslog统一管理&#xff0c;根据其主配置文件/etc/rsyslog.conf中设置决定内核消息及各种系统程序消息记录到什么位置。/var/log/message&#xff1a;该日志文件存放了内核消息…...

编程日记 2023/12/2 9:33:29

Redis主从复制实现RCE

文章目录 前置知识概念redis常用命令redis module 利用条件利用工具思路例题 [网鼎杯 2020 玄武组]SSRFMe总结 前置知识 概念 背景是多台服务器要保存同一份数据&#xff0c;如何实现其一致性呢&#xff1f;数据的读写操作是否每台服务器都可以处理&#xff1f;这里Redis就提供…...

编程日记 2023/12/2 9:23:20

Flutter应用程序的加固原理

在移动应用开发中&#xff0c;Flutter已经成为一种非常流行的技术选项&#xff0c;可以同时在Android和iOS平台上构建高性能、高质量的移动应用程序。但是&#xff0c;由于其跨平台特性&#xff0c;Flutter应用程序也面临着一些安全风险&#xff0c;例如反编译、代码泄露、数据…...

编程日记 2023/12/2 9:20:17

Centos7部署NFS

搭建NFS存储服务器--基于CentOS7系统 - jianmuzi - 博客园 在CentOS中搭建NFS - 陌上荼靡 - 博客园 NFS简介 NFS 是 Network FileSystem 的缩写&#xff0c;顾名思义就是网络文件存储系统&#xff0c;它最早是由 Sun 公司发展出来的&#xff0c;也是 FreeBSD 支持的文件系统…...

编程日记 2023/12/2 9:18:15

我已经开了一个融资融券的账户了，还可以再在别的券商开两融（信用账户）吗？

融资融券交易又称“证券信用交易”或保证金交易&#xff0c;是指投资者向具有融资融券业务资格的证券公司提供担保物&#xff0c;借入资金买入证券&#xff08;融资交易&#xff09;或借入证券并卖出&#xff08;融券交易&#xff09;的行为。 简单说就是融资做多&#xff0c;…...

编程日记 2023/12/2 9:14:12

Spring Cloud 版本升级记：OpenFeignClient与Gateway的爱恨交织

Spring Cloud 版本升级记&#xff1a;OpenFeignClient与Gateway的爱恨交织 近日&#xff0c;在负责的项目中&#xff0c;我对 Spring Boot、Spring Cloud 以及 Spring Cloud Alibaba 进行了版本升级。原以为会一切顺利&#xff0c;没想到却遭遇了 Spring Cloud Gateway 无法正…...

编程日记 2023/12/2 9:09:08

华为OD机试 - 最多购买宝石数目（Java JS Python C）

题目描述 橱窗里有一排宝石，不同的宝石对应不同的价格，宝石的价格标记为 gems[i] 0 ≤ i < nn = gems.length宝石可同时出售0个或多个，如果同时出售多个，则要求出售的宝石编号连续； 例如客户最大购买宝石个数为m，购买的宝石编号必须为：gems[i]，gems[i+1]，...，ge…...

编程日记 2023/12/2 9:08:07

【LeetCode】挑战100天 Day17（热题+面试经典150题）

【LeetCode】挑战100天 Day17&#xff08;热题面试经典150题&#xff09; 一、LeetCode介绍二、LeetCode 热题 HOT 100-192.1 题目2.2 题解 三、面试经典 150 题-193.1 题目3.2 题解 一、LeetCode介绍 LeetCode是一个在线编程网站&#xff0c;提供各种算法和数据结构的题目&…...

编程日记 2023/12/2 9:05:05