<蓝桥杯软件赛>零基础备赛20周--第8周第1讲--十大排序
报名明年4月蓝桥杯软件赛的同学们,如果你是大一零基础,目前懵懂中,不知该怎么办,可以看看本博客系列:备赛20周合集
20周的完整安排请点击:20周计划
每周发1个博客,共20周(读者可以按自己的进度选“正常”和“快进”两种计划)。
每周3次集中答疑,周三、周五、周日晚上,在QQ群上答疑:

文章目录
- 1. 选择排序
- 2. 冒泡排序
- 3. 插入排序
- 4. 希尔排序
- 5. 计数排序
- 6. 桶排序
- 7. 基数排序
- 8. 归并排序
- 9. 快速排序
- 10. 堆排序
第8周第1讲: 十大排序
排序是数据处理的基本操作,每次算法竞赛都必定用到排序。在绝大多数情况下,并不需要自己手写排序代码,而是直接用系统提供的函数sort()。
不过,还是强烈建议学习各种排序算法,掌握原理,自己实现代码,因为各种排序算法有不同的思路,很多算法来源于这些排序算法。
用下面的题目详解十种排序算法。
例题:排序
1. 选择排序
选择排序(Selection sort)是最简单直观的排序算法。
排序的目的是什么?对n个数从小到大排序,就是把杂乱无序的n个数,放到它们应该在的位置。
最简单的做法是:找到最小的数,放在第1个位置;找到第2小的数,放在第2个位置;…;找到第n大的数,放在第n个位置。
这个思路就是选择排序。具体操作:
(1)第一轮,在n个数中找到最小的数,然后与第1个位置的数交换。这样就把最小的数放到了第1个位置。

(2)第二轮,在第2 ~ 第n个数中找到最小的数,然后与2个位置的数交换。

…
一共执行n轮操作,第i轮找到第i大的数,放到第i个位置。结束。
C++代码
#include<bits/stdc++.h>
using namespace std;
int a[100005], n;
void selection_sort() {for (int i = 0; i < n-1; i++) { int m = i; //m: 记录a[i]~a[n-1]的最小数所在位置for (int j = i+1; j < n; j++) //找a[i]~a[n-1]的最小数if (a[j] < a[m]) m = j;swap(a[i], a[m]); //交换}
}
int main() {cin>>n;for (int i = 0; i < n; i++) scanf("%d", &a[i]);selection_sort();for (int i = 0; i < n; i++) printf("%d ", a[i]);return 0;
}
Java代码
import java.util.Scanner;
public class Main {static int a[] = new int[100005];static int n;public static void selection_sort() {for (int i = 0; i < n-1; i++) { //找a[i]~a[n-1]的最小数int m = i; //m: 记录a[i]~a[n-1]的最小数所在位置for (int j = i+1; j < n; j++)if (a[j] < a[m])m = j;int temp = a[i]; a[i] = a[m]; a[m] = temp; //交换}}public static void main(String[] args) {Scanner scanner = new Scanner(System.in);n = scanner.nextInt();for (int i = 0; i < n; i++) a[i] = scanner.nextInt();selection_sort();for (int i = 0; i < n; i++) System.out.print(a[i] + " ");}
}Python代码
def selection_sort():global a, nfor i in range(n-1):m = ifor j in range(i+1, n):if a[j] < a[m]: m = ja[i], a[m] = a[m], a[i] #交换
n = int(input())
a = list(map(int, input().split()))
selection_sort()
for i in range(n): print(a[i], end=" ")
选择排序算法的计算量是多少?找最小的数需要比较n-1次,找第2小的必要比较n-2次,…,一共需要比较约 n 2 / 2 n^2/2 n2/2次,把它的计算复杂度记为 O ( n 2 ) O(n^2) O(n2)。看代码也能分析出来,有两重for循环,分别循环约n次,共循环 O ( n 2 ) O(n^2) O(n2)次。
上述代码提交到判题系统,只能通过20%的测试。判题系统一般给一秒的执行时间,计算机一秒约能计算1亿次。本题若测试 n = 1 0 5 n=10^5 n=105个数,选择排序需要计算 n 2 n^2 n2=100亿次,超时。
选择排序是一种“死脑筋”的算法,它与原数列的特征无关,不管原数列是不是有序,都得计算 O ( n 2 ) O(n^2) O(n2)次。下一个“冒泡算法”就聪明得多,如果第一轮找最大数时发现数列已经有序,就停止不再做排序计算。
选择排序虽然低效,但也有优点:(1)简单易写;(2)不占用额外的空间,排序就在原来数列上操作。
2. 冒泡排序
冒泡排序(Bubble sort)也是一种简单直观的排序算法。它的原理和选择排序差不多:
第一轮,找到第1大的数,放在第n个位置;
第二轮,找到第2大的数,放在第n-1个位置;
…
第n轮,找到最小的数,放到第1个位置。
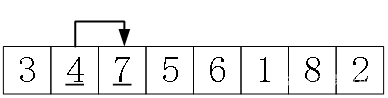
不过,与选择排序的简单粗暴相比,冒泡排序用到了“冒泡”这个小技巧。以“第一轮,找最大的数并放到第n个位置”为例,操作是:
(1)从第1个数a[0]开始,比较a[0]和a[1],如果a[0]>a[1],交换。这一步把前2个数中的大数放到了第2个位置。

(2)比较a[1]和a[2],如果a[1]>a[2],交换。这一步把前3个数中的最大数放到了第3个位置。
…
依次比较相邻的两个数,一直到最后的a[n-2]、a[n-1],就把最大的数放到了第n个位置。
这个过程形象地比喻为“冒泡”。
其他的数也用同样的方法处理,一共做n轮。第i轮找第i大的数并放到第i个位置,冒泡到a[i-1],就把第i大的数放到了第i个位置。
C++代码
#include<bits/stdc++.h>
using namespace std;
int a[100005], n;
void bubble_sort() {for (int i = 0; i < n-1; i++) {bool swapped = false; // 优化,如果某次比较没有发生交换,说明已经有序,结束for (int j = 0; j < n-i-1; j++)if (a[j] > a[j+1]) {swap(a[j], a[j+1]);swapped = true;}if (!swapped) break; //这一轮没有发生交换,说明已经有序,结束}
}
int main() {cin >> n;for (int i = 0; i < n; i++) scanf("%d", &a[i]);bubble_sort();for (int i = 0; i < n; i++) printf("%d ", a[i]);return 0;
}
冒泡算法的计算复杂度,第5行和第7行的两重for循环,计算复杂度为 O ( n 2 ) O(n^2) O(n2)。
冒泡算法可以做一点优化:若两个相邻的数已经有序,那么不用冒泡;在第i轮求第i大的数时,若一次冒泡都没有发生,说明整个数列已经有序,结束。代码第6行的swapped判断是否发生了冒泡。冒泡算法是“聪明”的排序算法。
Java代码
import java.util.Scanner;
public class Main {static int a[] = new int[100005];static int n;public static void bubble_sort() {boolean swapped;for (int i = 0; i < n-1; i++) {swapped = false;for (int j = 0; j < n-i-1; j++)if (a[j] > a[j+1]) {int temp = a[j]; a[j] = a[j+1]; a[j+1] = temp; //交换swapped = true;}if (!swapped) break;}}public static void main(String[] args) {Scanner scanner = new Scanner(System.in);n = scanner.nextInt();for (int i = 0; i < n; i++) a[i] = scanner.nextInt();bubble_sort();for (int i = 0; i < n; i++) System.out.print(a[i] + " ");}
}
Python代码
def bubble_sort():global a, nfor i in range(n-1):swapped = Falsefor j in range(n-i-1):if a[j] > a[j+1]:a[j], a[j+1] = a[j+1], a[j]swapped = Trueif not swapped: break
n = int(input())
a = list(map(int, input().split()))
bubble_sort()
for i in range(n): print(a[i], end=" ")
3. 插入排序
插入排序(Insertion sort)是一种“动态”算法:在一个有序数列上,新增一个数x,把它插入到有序数列中的合适位置,使数列仍保持有序。
如何插?简单的做法是,从有序数列的最后一个数开始,逐个与x比较,若这个数比x大,就继续往前找,直到找到比x小的数,把x插到它后面。
具体操作,以{3,7,4,5,6,1,8,2}为例:
(1)从第一个数a[0]开始。它构成了长度为1的有序数列{a[0]}。

(2)新增a[1],把它插到有序数列{a[0]}中。若a[1]≥a[0],完成。若a[1]<a[0],把a[1]插到a[0]前面,方法是:先把a[0]挪到数列的第2个位置,然后把a[1]放到数列第1个位置。得到新的有序数列{a[0], a[1]}。

(3)新增a[2],把它插到有序数列{a[0],a[1]}中。

…
下面是代码,概况执行过程:从a[1]开始遍历数组,将当前的数作为key,然后将它和前面的有序数列一一比较,如果发现前一个数大于key,则将它后移一位,直到找到一个前面的数不再大于key,就找到了key应该插入的位置,将key插入到该位置即可。
C++代码
#include<bits/stdc++.h>
using namespace std;
int a[100005], n;
void insertion_sort() {for (int i = 1; i < n; i++) {int key = a[i]; //记下a[i],准备把它插到前面合适的地方int j = i - 1; //i前面的数已经有序,把key插到合适位置while (j >= 0 && a[j] > key) { a[j+1] = a[j]; //如果key比a[j]小,就把a[j]往后挪,给key腾位置j--;}a[j+1] = key; //把key插到这里}
}
int main() {cin>>n;for (int i = 0; i < n; i++) scanf("%d", &a[i]);insertion_sort();for (int i = 0; i < n; i++) printf("%d ", a[i]);return 0;
}
插入排序的计算复杂度取决于第5行的for循环和第8行的while循环,这是两重循环,各循环O(n)次,总计算复杂度 O ( n 2 ) O(n^2) O(n2)。
插入排序是不是和冒泡排序一样“聪明”?也就是说,如果在一个有序的数列上运行插入排序算法,需要计算多少次?此时第8行的while的判断条件 a[j] > key始终不成立,while内的第9、10行不会执行,而第12行实际上就是a[i]=key,没有任何变化。那么for、while这两重循环实际上变成了只有for一个循环,一共计算O(n)次即结束。所以插入排序和冒泡排序一样“聪明”。
Java代码
import java.util.Scanner;
public class Main {static int a[] = new int[100005];static int n;public static void insertion_sort() {for (int i = 1; i < n; i++) {int key = a[i];int j = i - 1;while (j >= 0 && a[j] > key) {a[j+1] = a[j];j--;}a[j+1] = key;}}public static void main(String[] args) {Scanner scanner = new Scanner(System.in);n = scanner.nextInt();for (int i = 0; i < n; i++) a[i] = scanner.nextInt();insertion_sort();for (int i = 0; i < n; i++) System.out.print(a[i] + " ");}
}
Python代码
def insertion_sort():global a, nfor i in range(1, n):key = a[i]j = i - 1while j >= 0 and a[j] > key:a[j+1] = a[j]j -= 1a[j+1] = key
n = int(input())
a = list(map(int, input().split()))
insertion_sort()
for i in range(n): print(a[i], end=" ")
下一节的希尔排序是对插入排序的优化,其核心思想是让数列尽量有序,从而减少while循环。
4. 希尔排序
希尔排序(Shell sort)是一种基于插入排序的高效算法。
先给出代码,可以看到,shell_sort()仅仅是分多次做插入排序insertation_sort()。代码的关键处是称为“排序间距”的变量gap,通过多轮gap操作,减少了插入排序时的while循环的计算。
C++代码
#include<bits/stdc++.h>
using namespace std;
int a[100005], n;
void insertion_sort(int gap) { //插入排序for (int i = gap; i < n; i++){int key = a[i];int j = i-1;while(j >= gap-1 && a[j-gap+1] > key){a[j+1] = a[j-gap+1];j -= gap; //测试计算量,在这里统计: cnt++}a[j+1] = key;}
}
void shell_sort() { for (int gap = n/2; gap > 0; gap /= 2)insertion_sort(gap);
}
int main() {cin>>n;for (int i = 0; i < n; i++) scanf("%d", &a[i]);shell_sort();for (int i = 0; i < n; i++) printf("%d ", a[i]);return 0;
}
以int a[]={8, 7, 6, 5, 4, 3, 2, 1}这8个数从小到大排序为例,说明希尔排序的步骤。
(1)gap = 8/2 = 4,对间距为4的数排序。共有4组数的间距为4,这四组数分别是{8, 4}、{7, 3}、{6, 2}、{5, 1}。分别在这4组数内部做插入排序。例如{8, 4}做插入排序结果是{4, 8}。在这一轮,每组内的数做插入排序时都要进入代码第8行的while执行交换操作,共执行4次。经过这一轮操作,较大的数挪到了右边,更靠近它们排序后的终止位置。

(2)gap = 4/2 = 2,对间距为2的数排序。共有2组数的间距为2,分别是{4, 2, 8, 6}、{3, 1, 7, 5}。分别做插入排序,例如{4, 2, 8, 6}做插入排序的结果是{2, 4, 6, 8}。在这一轮,每组内的数做插入排序时,有些不需要进入代码第8行的while。例如处理8时,它前面的2、4已经排好序且更小,8不用做什么操作。这就是上一轮gap=4的排序操作带来的好处。

(3)gap = 2/2 = 1,对间距为1的数排序,实际上gap=1的希尔排序就是基本的插入排序。由于前2轮的操作,到这一轮有很多数不用进入代码第8行的while,例如{4, 6, 8}这3个数。即使进入了while,也只需做极少的交换操作,例如处理到{5}时,它前面已经得到{1, 2, 3, 4, 6},那么{5}只需要插到{6}前面即可。

希尔排序在多大程度上改善了插入排序?可以直接对比两个代码的计算量。定义一个全局变量cnt,在insertion_sort()的while中累加cnt,统计进入了多少次while。输入数列{8, 7, 6, 5, 4, 3, 2, 1},分别执行上一节的插入排序和这一节的希尔排序,得插入排序cnt = 28次,希尔排序cnt = 12。希尔排序显然好很多。
根据严格的算法分析,希尔排序的计算复杂度约为 O ( n 1.5 ) O(n^{1.5}) O(n1.5)。当 n = 1 0 5 n = 10^5 n=105时,计算量约3000万次,远远小于 O ( n 2 ) O(n^2) O(n2)的100亿次。
最后概况希尔排序的思路。希尔排序是一种基于插入排序的排序算法,它将一个序列分成若干个子序列,对每个子序列使用插入排序,最后再对整个序列使用一次插入排序。函数shell_sort()使用gap对数组进行分组,然后对每个子序列使用插入排序,最后将整个序列使用插入排序。在插入排序的过程中,每次将元素插入到已经排好序的序列中,而这个已经排好序的序列是由前面的插入排序操作得到的,每次操作都相当于将元素插入到一个较小的序列中,因此可以更快地将元素插入到正确的位置上。
Java代码
import java.util.Scanner;
public class Main {static int a[] = new int[100005];static int n;public static void insertion_sort(int gap) {for (int i = gap; i < n; i++){int key = a[i];int j = i-1;while(j >= gap-1 && a[j-gap+1] > key){a[j+1] = a[j-gap+1];j -= gap;}a[j+1] = key;}}public static void shell_sort() {for (int gap = n/2; gap > 0; gap /= 2)insertion_sort(gap);}public static void main(String[] args) {Scanner scanner = new Scanner(System.in);n = scanner.nextInt();for (int i = 0; i < n; i++) a[i] = scanner.nextInt();shell_sort();for (int i = 0; i < n; i++) System.out.print(a[i] + " ");}
}
Python代码
def insertion_sort(gap):global a, nfor i in range(gap, n):key = a[i]j = i-1while j >= gap-1 and a[j-gap+1] > key:a[j+1] = a[j-gap+1]j -= gapa[j+1] = key
def shell_sort(): for gap in range(n//2, 0, -1): insertion_sort(gap)
n = int(input())
a = list(map(int, input().split()))
shell_sort()
for i in range(n): print(a[i], end=" ")
5. 计数排序
计数排序(Counting Sort)是基于哈希思想的一种排序算法,它使用一个额外的数组来统计每个数出现的次数,然后基于次数输出排序后的数组。
以数列a[] = {5,2,7,3,4,3}为例说明计数排序的操作步骤。
(1)找到数列的最大值7,建计数数组cnt[8];
(2)把数列中的每个数看成cnt[i]的下标i,对应的cnt[i]计数。例如{5}对应cnt[5]=1,{2}对应cnt[2]=1,2个{3}对应cnt[3]=2,等等。

(3)遍历cnt[],若cnt[i]=k,输出k次i。输出结果就是排序结果。
概况地说,计数排序是一种非比较性的排序算法,它利用元素的值作为键值确定元素在序列中出现的次数,从而实现排序。
C++代码
#include<bits/stdc++.h>
using namespace std;
int a[100005], n;
void counting_sort() {int i;int max = a[0];for (i = 1; i < n; i++) //找到最大值if (a[i] > max) max = a[i];int* cnt = (int*) calloc(max+1, sizeof(int)); //建数组cnt[]for (i = 0; i < n; i++) cnt[a[i]]++; //把a[i]放到对应的空间里i = 0;for (int j = 0; j <= max; j++) //输出排序的结果while (cnt[j] > 0){a[i++] = j;cnt[j]--;}free(cnt);
}
int main() {cin>>n;for (int i = 0; i < n; i++) scanf("%d", &a[i]);counting_sort();for (int i = 0; i < n; i++) printf("%d ", a[i]);return 0;
}
该函数首先遍历数组,找到数组中的最大值max,然后创建计数数组cnt[],大小为 max+1,用于存储元素出现的次数。然后遍历数组,把每个数的出现次数存储在计数数组中。最后遍历计数数组,将数组中的元素按照次数从小到大依次输出,从而得到一个有序数组。
计数排序的时间复杂度取决于第12行的for循环,共循环max次,计算量由max决定。
这使得计数排序的应用场景非常狭窄,只适合“小而紧凑”的数列,当所有的数值都不太大,且均匀分布时,计数排序才有好的效果。例如 n = 1 0 5 n=10^5 n=105,且 0 < a [ i ] < 1 0 5 0<a[i]<10^5 0<a[i]<105时,效率极高,可以在O(n)的时间内排序。
如果数列的数值很大,就不适合用计数排序。此时需要创建极大的数组cnt[],不仅浪费空间,而且计算时间极长。例如对{5, 1 0 9 10^9 109}排序,虽然只有2个数,却需要建长度为 1 0 9 10^9 109=1G的数组,且需要在代码第12行循环 1 0 9 10^9 109次。
代码提交到判题系统,有40%的测试返回Memory Limit Exceeded,说明代码对这40%的测试数据排序时使用的空间超出了内存限制。
Java代码
import java.util.Scanner;
public class Main {static int a[] = new int[100005];static int n;public static void counting_sort() {int i;int max = a[0];for (i = 1; i < n; i++)if (a[i] > max) max = a[i];int[] cnt = new int[max+1];for (i = 0; i < n; i++) cnt[a[i]]++;i = 0;for (int j = 0; j <= max; j++)while (cnt[j] > 0){a[i++] = j;cnt[j]--;}}public static void main(String[] args) {Scanner scanner = new Scanner(System.in);n = scanner.nextInt();for (int i = 0; i < n; i++) a[i] = scanner.nextInt();counting_sort();for (int i = 0; i < n; i++) System.out.print(a[i] + " ");}
}
Python代码
def counting_sort():global a, nmax_num = max(a)cnt = [0] * (max_num+1)for i in range(n): cnt[a[i]] += 1i = 0for j in range(max_num+1):while cnt[j] > 0:a[i] = ji += 1cnt[j] -= 1
n = int(input())
a = list(map(int, input().split()))
counting_sort()
for i in range(n): print(a[i], end=" ")
6. 桶排序
桶排序(Bucket sort)是分治思想的应用,它的要点是:
(1)有k个桶,把要排序的n个数尽量均匀分到每个桶中;
(2)要求桶之间也是有序的,即第i个桶内所有的数小于第i+1个桶内所有的数;
(3)在每个桶内部排序;
(4)最后把所有的桶合起来,就是排序的结果。
例如有100个数,这些数的大小在1~100之间,把它们分到10个桶中,第1个桶放1~10内的数,第2个桶放11~20内的数,…,等等。然后分别在每个桶内排序,最后把所有的桶的数合起来输出,就是排序的结果。
为什么分成多个桶然后在各桶内排序,能提高效率?这就是分治的威力,下面做个简单分析。设有一个排序算法,计算复杂度为 O ( n 2 ) O(n^2) O(n2)。把这n个数分到k个桶中,每个桶装 n k \frac{n}{k} kn个数,且第i个桶的所有数小于第i+1个桶的所有数。每个桶内排序的计算量是 n 2 k 2 \frac{n^2}{k^2} k2n2,k个桶的总计算量是 k × n 2 k 2 = n 2 k k\times\frac{n^2}{k^2}=\frac{n^2}{k} k×k2n2=kn2。所以结论是,利用k个桶进行分治,能把原来 O ( n 2 ) O(n^2) O(n2)的计算量减少到 O ( n 2 k ) O(\frac{n^2}{k}) O(kn2),优化了k倍。
不过,桶排序并不是一个简单的算法,它的性能取决于:
(1)桶的数量k。要求k≤n,极端情况下k=n,且一个桶内只有一个数,那么总计算量就减少到了O(n),达到了最优的计算复杂度。但是太多的桶可能需要大量的存储空间,所以需要设定一个合适的k。
(2)保证桶之间也是有序的,即让第i个桶的所有数小于第i+1个桶的所有数。简单的做法是按数字的大小分到每个桶里。例如数的大小在1~100之间,设置k=10个桶,第1个桶放1~10内的数,第2个桶放11~20内的数,…,等等。这样桶之间就有序了。但是这个简单的方法可能导致分布不均衡,有些桶内数太少,有些桶内数太多。
(3)快速地把n个数分开放到k个桶中。桶排序的总时间包括两部分:把n个数分到k个桶的时间,以及分别在k个桶内排序的时间。如果前者耗时太长,也影响桶排序的性能。
(4)均匀地把n个数分开放到k个桶中。只有均匀分布,才能发挥分治的威力。而极端情况下,有可能所有的数都分到了1个桶里,其他桶都是空的,等于没有分桶。例如100个数,第1个数是1,其他数都在90~100之间,把这100个数分到10个桶里,第1个桶放1~10的数,第2个桶放11~20内的数,…,第10个桶放90~100的数,那么结果是第1个桶内有1个数,第10个桶有99个数,其他桶是空的。这样的分桶毫无意义。所以需要设计一个合理的分桶算法。
(5)桶内排序。在桶内的排序,选用适合的算法会更高效。
由于上述原因,桶排序不是一个简单的算法,而是多个技术的综合,所以本节没有给出代码。
上一节的计数排序可以看作桶排序的一个特例,此时k远远大于n,大部分桶是空的。
7. 基数排序
基数排序(Radix sort)是一种非比较性的排序算法,它不是直接比较各数据的大小,而是按照数据的位数依次进行排序。
“基数”指的是每个元素的进制位上的取值范围。例如,对于十进制数,每个元素的进制位上的取值范围是0~9,因此基数为10;对于二进制数,每个元素的进制位上的取值范围是0~1,因此基数为2。
有两种基数排序:最低位优先法 (LSD, Least Significant Digit first)、最高位优先法 (MSD, Most Significant Digit first)。这里介绍较为简单的LSD基数排序。
LSD基数排序是一种反常识的排序方法,它不是先比较高位再比较低位,而是反过来,先比较低位再比较高位。例如排序{5, 47, 23, 19, 17, 31}。
第1步:先按个位的大小排序,得到{31, 23, 05, 47, 17, 19}。
第2步:再按十位的大小排序,得到{05, 17, 19, 23, 31, 47}。其中5只有个位,把它的十位补0。基数排序需要将所有待比较的数值统一为同样的数位长度,如果某些数的位不够,在前面补零即可。
因为所有数字中最大的只有两位,所以只需2步就结束,得到有序排列。
更特别的是,上述操作并不是用比较的方法得到的,而是用“哈希”的思路:直接把数字放到对应的“桶”里。有10个桶,分别标记为0~9。第1步按个位的数字放,第2步按十位的数字放。下表中第2步得到的序列就是结果。

基数排序的复杂度:n个数,每个数有d位(例如上面例子的17 ~ 47,都是2位数),每一位有k种可能(十进制,0~9共十种情况)。复杂度是O(d*(n+k)),存储空间是O(n+k)。例如对长度10000的字符串进行一次后缀排序,n = 10000,d ≤ 5,k = 10,复杂度d*(n+k) ≈ 10000*5。而一次快排的复杂度nlogn ≈ 10000*13。
对比快速排序等排序方法,基数排序在d比较小的情况下,即所有的数字差不多大时,是更好的方法。如果d比较大,基数排序并不比快速排序更好。
LSD基数排序也可以看成桶排序的一个特例,上面处理十进制的0~9,基数为10,就是10个桶。
当基数为其他数值时,桶的数量也不同。例如:
(1)把数字看成二进制,每一位是0~1,基数为2,有2个桶。
(2)把数字看成二进制,并且把它按每16位划分,例如数字0xE1BE13DC34,划分成00E1-BE13-DC34,16位二进制范围0~65535,基数为65536,有65536个桶。这样做的好处是可以用位操作来处理,速度稍快一些。
(3)对字符串排序,一个字符串的一个字符是char型,8位二进制范围0~255,基数256,就是256个桶。
下面给出例题的LSD基数排序的代码。函数radix_sort()首先遍历数组,找到数组中的最大值max,然后使用exp记录当前排序的位数,从个位开始,依次按照位数进行排序,直到最高位。在每次排序中,使用计数排序的方法,将元素分配到桶中,然后按照桶的顺序将元素重新排序。最后将排序后的数组复制到原数组中。
C++代码
#include<bits/stdc++.h>
using namespace std;
int a[100005], tmp[100005],n;
void radix_sort() {int exp = 1;int max = a[0];for (int i = 1; i < n; i++) //找出最大值,目的是找到最大数有多少位if (a[i] > max) max = a[i];while (max / exp > 0) { //从个位开始,一直到最高位int bucket[10] = {0};for (int i = 0; i < n; i++) bucket[(a[i] / exp) % 10]++;for (int i = 1; i < 10; i++) bucket[i] += bucket[i-1];for (int i = n-1; i >= 0; i--) {int k = (a[i] / exp) % 10;tmp[bucket[k]-1] = a[i];bucket[k]--;}for (int i = 0; i < n; i++) a[i] = tmp[i];exp *= 10;}
}
int main() {cin>>n;for (int i = 0; i < n; i++) scanf("%d", &a[i]);radix_sort();for (int i = 0; i < n; i++) printf("%d ", a[i]);return 0;
}
Java代码
import java.util.Scanner;
public class Main {static int a[] = new int[100005];static int tmp[] = new int[100005];static int n;public static void radix_sort() {int exp = 1;int max = a[0];for (int i = 1; i < n; i++)if (a[i] > max) max = a[i];while (max / exp > 0) {int bucket[] = new int[10];for (int i = 0; i < n; i++) bucket[(a[i] / exp) % 10]++;for (int i = 1; i < 10; i++) bucket[i] += bucket[i-1];for (int i = n-1; i >= 0; i--) {int k = (a[i] / exp) % 10;tmp[bucket[k]-1] = a[i];bucket[k]--;}for (int i = 0; i < n; i++) a[i] = tmp[i];exp *= 10;}}public static void main(String[] args) {Scanner scanner = new Scanner(System.in);n = scanner.nextInt();for (int i = 0; i < n; i++) a[i] = scanner.nextInt();radix_sort();for (int i = 0; i < n; i++) System.out.print(a[i] + " ");}
}
Python代码
def radix_sort():global a, n exp = 1max_num = max(a)tmp = [0] * len(a) while max_num // exp > 0:bucket = [0] * 10for i in range(n): bucket[(a[i] // exp) % 10] += 1for i in range(1, 10): bucket[i] += bucket[i-1]for i in range(n-1, -1, -1):k = (a[i] // exp) % 10tmp[bucket[k]-1] = a[i]bucket[k] -= 1for i in range(n): a[i] = tmp[i]exp *= 10
n = int(input())
a = list(map(int, input().split()))
radix_sort()
for i in range(n): print(a[i], end=" ")
基数排序的计算复杂度证明,参考《算法导论》:

8. 归并排序
归并排序(Merge sort)和下一小节的快速排序是分治法思想的应用,极为精美。学习它们,对于理解分治法、提高算法思维能力,十分有帮助。
先思考一个问题:如何用分治思想设计排序算法?
根据分治法的分解、解决、合并三步骤,具体思路如下:
(1)分解。把原来无序的数列,分成两部分;对每个部分,再继续分解成更小的两部分……在归并排序中,只是简单地把数列分成两半。在快速排序中,是把序列分成左右两部分,左部分的元素都小于右部分的元素;分解操作是快速排序的核心操作。
(2)解决。分解到最后不能再分解,排序。
(3)合并。把每次分开的两个部分合并到一起。归并排序的核心操作是合并,其过程类似于交换排序。快速排序并不需要合并操作,因为在分解过程中,左右部分已经是有序的。
下图的例子给出了归并排序的操作步骤。初始数列经过3趟归并之后,得到一个从小到大的有序数列。
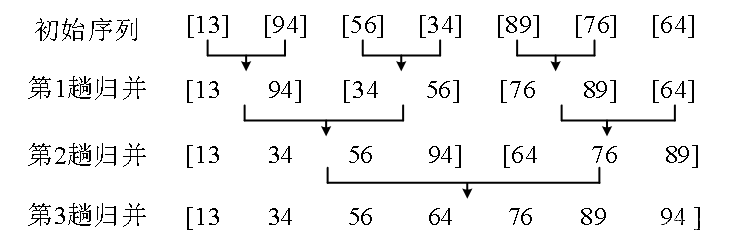
归并排序的主要操作:
(1)分解。把初始序列分成长度相同的左右两个子序列,然后把每个子序列再分成更小的两个子序列……,直到子序列只包含1个数。这个过程用递归实现,上图中的第一行是初始序列,每个数是一个子序列,可以看成递归到达的最底层。
(2)求解子问题,对子序列排序。最底层的子序列只包含1个数,其实不用排序。
(3)合并。归并两个有序的子序列,这是归并排序的主要操作,过程如下图。例如图 (1)中, i和j分别指向子序列{13, 94, 99}和{34, 56}的第1个数,进行第一次比较,发现a[i] < a[j],把a[i]放到临时空间b[]中。总共经过四次比较,得到b[] = {13, 34 ,56, 94, 99}。

下面分析归并排序的计算复杂度。对n个数进行归并排序:(1)需要logn趟归并;(2)在每一趟归并中,有很多次合并操作,一共需要O(n)次比较。总计算复杂度是O(nlogn)。
空间复杂度:由于需要一个临时的b[]存储结果,所以空间复杂度是O(n)。
C++代码
#include<bits/stdc++.h>
using namespace std;
int a[100005], b[100005], n;
void Merge(int L, int mid, int R){int i=L, j = mid+1, t=0;while(i <= mid && j <= R){if(a[i] > a[j]) b[t++] = a[j++];else b[t++]=a[i++];}//一个子序列中的数都处理完了,另一个还没有,把剩下的直接复制过来:while(i <= mid) b[t++]=a[i++];while(j <= R) b[t++]=a[j++];for(i=0; i<t; i++) a[L+i] = b[i]; //把排好序的b[]复制回a[]
}
void Mergesort(int L, int R){if(L<R){int mid = (L+R)/2; //平分成两个子序列Mergesort(L, mid);Mergesort(mid+1, R);Merge(L, mid, R); //合并}
}
int main() {cin>>n;for (int i = 0; i < n; i++) scanf("%d", &a[i]);Mergesort(0,n-1);for (int i = 0; i < n; i++) printf("%d ", a[i]);return 0;
}
Java代码
import java.util.Scanner;
public class Main {static int a[] = new int[100005];static int b[] = new int[100005];static int n;public static void Merge(int L, int mid, int R){int i=L, j = mid+1, t=0;while(i <= mid && j <= R){if(a[i] > a[j]) b[t++] = a[j++];else b[t++]=a[i++];}while(i <= mid) b[t++]=a[i++];while(j <= R) b[t++]=a[j++];for(i=0; i<t; i++) a[L+i] = b[i];}public static void Mergesort(int L, int R){if(L<R){int mid = (L+R)/2;Mergesort(L, mid);Mergesort(mid+1, R);Merge(L, mid, R);}}public static void main(String[] args) {Scanner scanner = new Scanner(System.in);n = scanner.nextInt();for (int i = 0; i < n; i++) a[i] = scanner.nextInt();Mergesort(0,n-1);for (int i = 0; i < n; i++) System.out.print(a[i] + " ");}
}Python代码
def Merge(L, mid, R):global a, bi=Lj = mid+1t=0while(i <= mid and j <= R):if(a[i] > a[j]):b[t] = a[j]j += 1else:b[t] = a[i]i += 1t += 1while(i <= mid):b[t] = a[i]i += 1t += 1while(j <= R):b[t] = a[j]j += 1t += 1for i in range(t): a[L+i] = b[i]
def Mergesort(L, R):if L < R:mid = (L+R)//2Mergesort(L, mid)Mergesort(mid+1, R)Merge(L, mid, R)
n = int(input())
a = list(map(int, input().split()))
b = [0] * len(a)
Mergesort(0,n-1)
for i in range(n): print(a[i], end=" ")
9. 快速排序
上一节提到,快速排序(Quick sort)和归并排序都是分治法的应用。
快速排序的思路是:把序列分成左右两部分,使得左边所有的数都比右边的数小;递归这个过程,直到不能再分为止。如何把序列分成左右两部分?最简单的办法是设定两个临时空间X、Y和一个基准数t;检查序列中所有的元素,比t小的放在X中,比t大的放在Y中。不过,其实不用这么麻烦,直接在原序列上操作就行了,不需要使用临时空间X、Y。
直接在原序列上进行划分的方法有很多种,下面的图示介绍了一种很容易操作的方法:

下面分析复杂度。
每一次划分,都把序列分成了左右两部分,在这个过程中,需要比较所有的元素,有O(n)次。如果每次划分是对称的,也就是说左右两部分的长度差不多,那么一共需要划分O(logn)次。总复杂度O(nlogn)。
如果划分不是对称的,左部分和右部分的数量差别很大,那么复杂度会高一些。在极端情况下,例如左部分只有1个数,剩下的全部都在右部分,那么最多可能划分n次,总复杂度是 O ( n 2 ) O(n^2) O(n2)。所以,快速排序的效率和数据本身有关。
不过,一般情况下快速排序效率很高,甚至比归并排序更好。读者可以观察到,下面给出的快速排序的代码比归并排序的代码更简洁,代码中的比较、交换、拷贝操作很少。 快速排序几乎是目前所有排序法中速度最快的方法。STL的sort()函数就是基于快速排序算法的,并针对快速排序的缺点做了很多优化。
C++代码
#include<bits/stdc++.h>
using namespace std;
int a[100005],n;
void qsort(int L,int R){int i=L,j=R;int key=a[(L+R)/2];while(i<=j) {while(a[i]<key) i++;while(a[j]>key) j--;if(i<=j){swap(a[i],a[j]);i++; j--;}}if(j>L) qsort(L,j);if(i<R) qsort(i,R);
}
int main(){cin>>n;for(int i=0;i<n;i++) scanf("%d",&a[i]);qsort(0,n-1);for(int i=0;i<n;i++) printf("%d ",a[i]);return 0;
}
Java代码
import java.util.Scanner;
public class Main {static int[] a = new int[100005];static int n;public static void qsort(int L, int R) {int i = L, j = R;int key = a[(L + R) / 2];while (i <= j) {while (a[i] < key) i++;while (a[j] > key) j--;if (i <= j) {int temp = a[i];a[i] = a[j];a[j] = temp;i++;j--;}}if (j > L) qsort(L, j);if (i < R) qsort(i, R);}public static void main(String[] args) {Scanner input = new Scanner(System.in);n = input.nextInt();for (int i = 0; i < n; i++) a[i] = input.nextInt();qsort(0, n - 1);for (int i = 0; i < n; i++) System.out.print(a[i] + " ");}
}
Python代码
def qsort(L, R):i, j = L, Rkey = a[(L + R) // 2]while i <= j:while a[i] < key: i += 1while a[j] > key: j -= 1if i <= j:a[i], a[j] = a[j], a[i]i += 1j -= 1if j > L: qsort(L, j)if i < R: qsort(i, R)
n = int(input())
a = list(map(int, input().split()))
qsort(0,n-1)
for i in range(n): print(a[i], end=" ")
10. 堆排序
堆排序(heap sort)利用二叉堆的属性来排序。二叉堆是一棵二叉树,如果是一棵最小堆,那么树根是最小值。把树根取出后,新的树根仍然是剩下的树上的最小值。首先把需要排序的n个数放进二叉堆,然后依次取出树根,就从小到大排好了序。由于把数放进二叉堆和取出二叉堆,计算复杂度都是O(logn)的,所以n个数的总复杂度是O(nlogn)的。
由于自己编程实现二叉堆比较麻烦,这里直接使用优先队列。优先队列是用二叉堆实现的。
C++代码
#include<bits/stdc++.h>
using namespace std;
int main() {int n; cin >> n;priority_queue<int, vector<int>, greater<int>> pq; // 优先队列,是小根堆for (int i = 0; i < n; i++) {int a; cin >> a;pq.push(a); // 将输入的数插入小根堆}while (!pq.empty()) {cout << pq.top() << " "; // 依次输出堆顶元素(树根),就是从小到大输出pq.pop(); // 弹出堆顶元素}return 0;
}
Java代码
import java.util.PriorityQueue;
import java.util.Scanner;
public class Main {public static void main(String[] args) {Scanner input = new Scanner(System.in);int n = input.nextInt();PriorityQueue<Integer> pq = new PriorityQueue<Integer>();for (int i = 0; i < n; i++) {int a = input.nextInt();pq.offer(a);}while (!pq.isEmpty())System.out.print(pq.poll() + " ");}
}
Python代码
import queue
n = int(input())
a = list(map(int, input().split()))
pq = queue.PriorityQueue()
for i in range(n): pq.put(a[i])
while not pq.empty(): print(pq.get(), end=' ')
相关文章:

<蓝桥杯软件赛>零基础备赛20周--第8周第1讲--十大排序
报名明年4月蓝桥杯软件赛的同学们,如果你是大一零基础,目前懵懂中,不知该怎么办,可以看看本博客系列:备赛20周合集 20周的完整安排请点击:20周计划 每周发1个博客,共20周(读者可以按…...

数据增强让模型更健壮
在做一些图像分类训练任务时,我们经常会遇到一个很尴尬的情况,那就是: 明明训练数据集中有很多可爱猫咪的照片,但是当我们给训练好的模型输入一张戴着头盔的猫咪进行测试时,模型就不认识了,或者说识别精度很低。 很明显,模型的泛化能力太差,难道戴着头盔的猫咪就不是猫…...

Redis远程字典服务
1 介绍 Redis(Remote Dictionary Server)是一个开源的内存数据存储系统,可以用作数据库、缓存和消息中间件。它支持多种数据结构,包括字符串(strings)、哈希表(hashes)、列表&#…...
Hdoop学习笔记(HDP)-Part.15 安装HIVE
目录 Part.01 关于HDP Part.02 核心组件原理 Part.03 资源规划 Part.04 基础环境配置 Part.05 Yum源配置 Part.06 安装OracleJDK Part.07 安装MySQL Part.08 部署Ambari集群 Part.09 安装OpenLDAP Part.10 创建集群 Part.11 安装Kerberos Part.12 安装HDFS Part.13 安装Ranger …...

vue3+element-plus之el-date-picker日期选择器清空无回调的解决方案
MENU 前言解决htmlJavaScrip 前言 在一个任务列表的搜索栏,添加一个日期区间搜索。使用到element-plus中的日期选择器el-date-picker;el-date-picker本身方法中有change事件,但是清空按钮没有对应回调方法。在任务列表的搜索需求中࿰…...
【虚拟机】Docker基础 【二】
2.2.数据卷 容器是隔离环境,容器内程序的文件、配置、运行时产生的容器都在容器内部,我们要读写容器内的文件非常不方便。大家思考几个问题: 如果要升级MySQL版本,需要销毁旧容器,那么数据岂不是跟着被销毁了&#x…...

CSS 绝对定位问题和粘性定位介绍
目录 1,绝对定位问题1,绝对定位元素的特性2,初始包含块问题 2,粘性定位注意点: 1,绝对定位问题 1,绝对定位元素的特性 display 默认为 block。所以行内元素设置绝对定位后可直接设置宽高。脱离…...

matlab 计算两点云之间的放缩倍数
目录 一、算法原理1、原理概述2、参考文献二、代码实现三、结果展示本文由CSDN点云侠原创,原文链接。如果你不是在点云侠的博客中看到该文章,那么此处便是不要脸的爬虫与GPT。 一、算法原理 1、原理概述 放缩倍数即尺度参数,尺度参数可由2个公共点在不同坐标系下的距离之…...

MySQL-数据库设计与实现
目录 第1关:从概念模型到MySQL实现 第2关:从需求分析到逻辑模型 第3关:建模工具的使用 第1关:从概念模型到MySQL实现 任务描述 将已建好的概念模型,变成MySQL物理实现。 # 请将你实现flight_booking数据库的语句写…...

后端返回图片流前端展示图片
根据后端返回的图片流格式,选用合适方法转换 下面以base64为例 if(res.status 200) {res.data.data.forEach((item,index) > {let Array data:image/png;base64, itemlet blob this.base64toBlob(Array)let url URL.createObjectURL(blob)this.imageList.p…...

解决 from . import _imaging as core ImportError: DLL load failed: 找不到指定的模块。
升级pillow版本就完事了 卸载掉之前的旧版本 conda uninstall pillow升级到新的版本就解决了 pip uninstall pillow 那个错误就解决了...

springBoot3.2 + jdk21 + GraalVM上手体验
springBoot3.2 jdk21 GraalVM上手体验 SpringBoot2.x官方已经停止维护了,jdk8这次真的得换了🤣 可以参考官方文章进行体验:https://spring.io/blog/2023/09/09/all-together-now-spring-boot-3-2-graalvm-native-images-java-21-and-virt…...
)的用法,web中的应用)
Python float(input())的用法,web中的应用
float(input()) 要理解Python中的float(input()),可以分两部分。第一,input()用于获取键盘上的输入,该函数的返回值是一个Python字符串str类型的数据——不过输入的是什么;第二,float()函数用于将传递的参数——这里就…...
uniapp是否可以用elementUI等前端UI库、使用步骤以及需要注意的问题
文章目录 uniapp是否可以用elementUI等前端UI库使用方法和步骤问题如何解决 uniapp是否可以用elementUI等前端UI库 在PC端开发uniapp,可以用elementUI,因为elementUI就是PC端的。 在使用uniapp,选择vue2.0时,实测可以用nodejs16的…...

在vue中如何书写 SSR 友好的代码
文章目录 前言服务端的响应性组件生命周期钩子访问平台特有 API跨请求状态污染激活不匹配自定义指令teleports后言 前言 hello world欢迎来到前端的新世界 😜当前文章系列专栏:vue.js 🐱👓博主在前端领域还有很多…...

开源与闭源:数字时代大模型之辩
欢迎大家到我的博客浏览更多文章。YinKais Blog | YinKais Blog 大模型的未来:开源与闭源的博弈 在大模型的发展中,开源和闭源两种截然不同的开发模式发挥着重要的作用。开源以其技术共享的特性,吸引了大量人才参与,推动了大模型的…...

卷积神经网络(VGG-16)猫狗识别
文章目录 一、前言二、前期工作1. 设置GPU(如果使用的是CPU可以忽略这步)2. 导入数据3. 查看数据 二、数据预处理1. 加载数据2. 再次检查数据3. 配置数据集4. 可视化数据 三、构建VG-16网络四、编译五、训练模型六、模型评估七、保存and加载模型八、预测…...
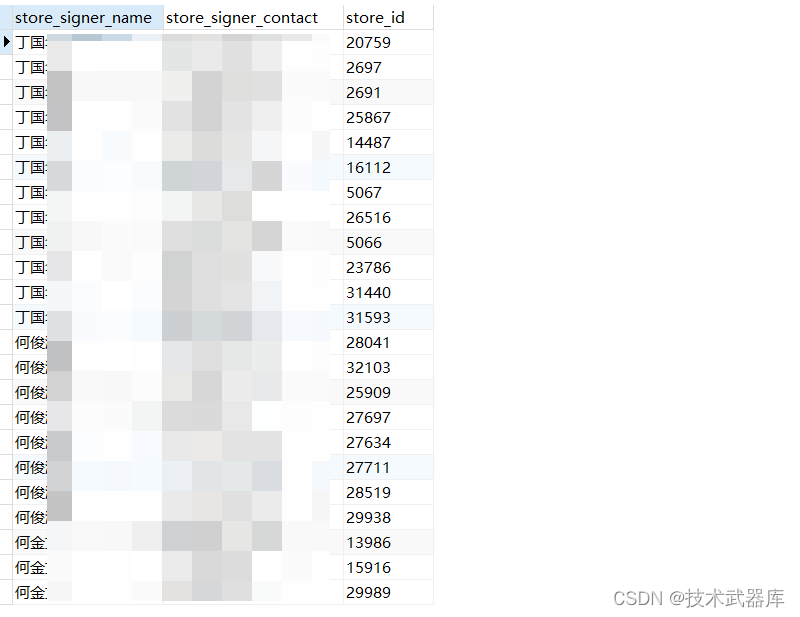
Mysql 行转列,把逗号分隔的字段拆分成多行
目录 效果如下源数据变更后的数据 方法第一种示例SQL和业务结合在一起使用 第二种示例SQL和业务结合在一起使用 结论 效果如下 源数据 变更后的数据 方法 第一种 先执行下面的SQL,看不看能不能执行,如果有结果,代表数据库版本是可以的&…...
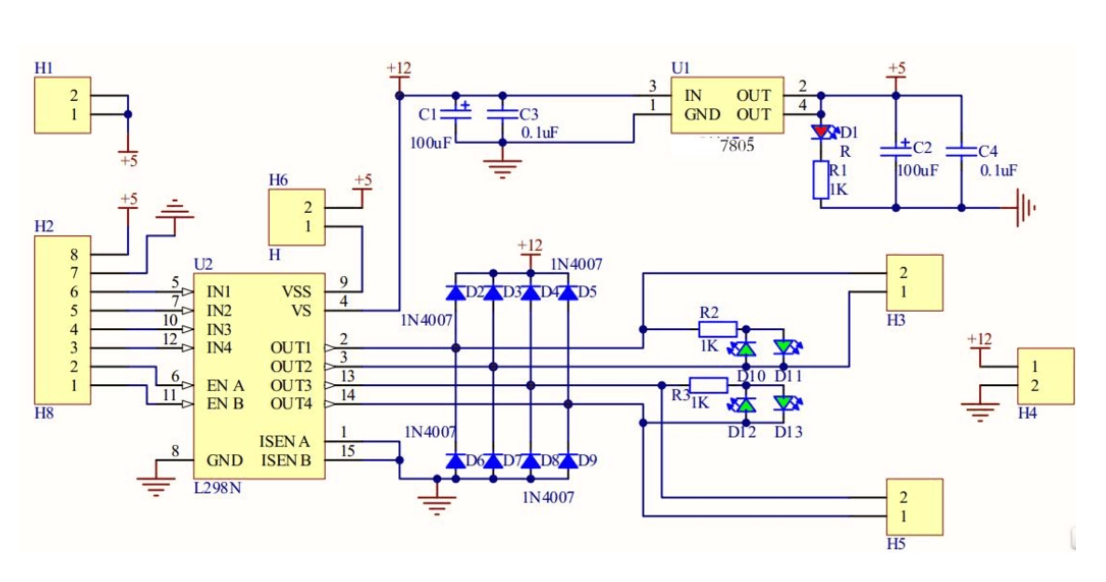
基于单片机设计的智能水泵控制器
一、前言 在一些场景中,如水池、水箱等水体容器的管理中,保持水位的稳定是至关重要的。传统上,人们通常需要手动监测水位并进行水泵的启停控制,这种方式不仅效率低下,还可能导致水位过高或过低,从而对水体…...
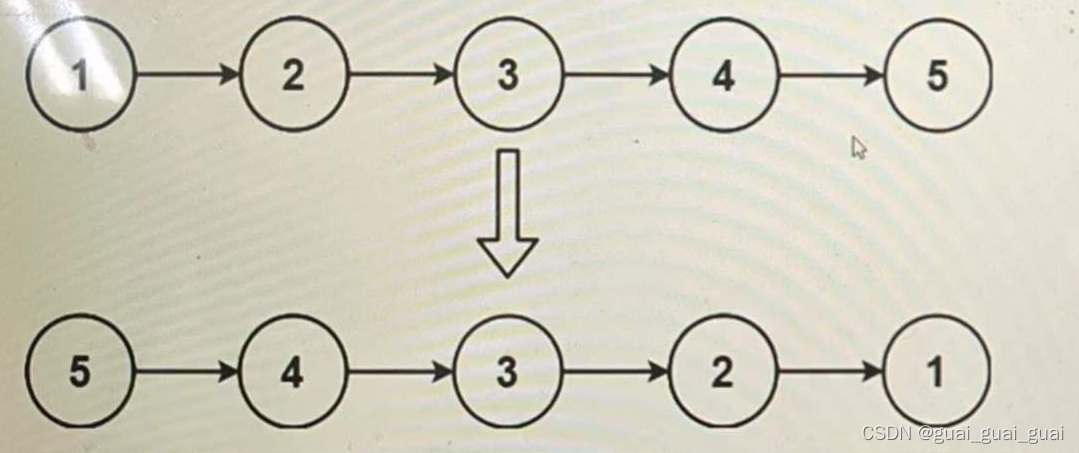
反转链表的实现
题目描述: 给出一个链表的头节点,将其反转,并返回新的头节点 思路1:反转地址 将每个节点里的地址由指向下一个节点变为指向前一个节点 定义三个结构体指针n1,n2,n3,n1表示改后指针的地址,n2表示要修改结构体里next的…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...

c# 局部函数 定义、功能与示例
C# 局部函数:定义、功能与示例 1. 定义与功能 局部函数(Local Function)是嵌套在另一个方法内部的私有方法,仅在包含它的方法内可见。 • 作用:封装仅用于当前方法的逻辑,避免污染类作用域,提升…...

GraphQL 实战篇:Apollo Client 配置与缓存
GraphQL 实战篇:Apollo Client 配置与缓存 上一篇:GraphQL 入门篇:基础查询语法 依旧和上一篇的笔记一样,主实操,没啥过多的细节讲解,代码具体在: https://github.com/GoldenaArcher/graphql…...

负载均衡器》》LVS、Nginx、HAproxy 区别
虚拟主机 先4,后7...
