【数据结构和算法】无限集中的最小数字
其他系列文章导航
Java基础合集
设计模式合集
多线程合集
分布式合集
ES合集
文章目录
其他系列文章导航
文章目录
前言
一、题目描述
二、题解
三、代码
四、总结
前言
这是力扣的2336题,难度为中等,解题方案有很多种,本文讲解我认为最奇妙的一种。
一、题目描述
现有一个包含所有正整数的集合 [1, 2, 3, 4, 5, ...] 。
实现 SmallestInfiniteSet 类:
SmallestInfiniteSet()初始化 SmallestInfiniteSet 对象以包含 所有 正整数。int popSmallest()移除 并返回该无限集中的最小整数。void addBack(int num)如果正整数num不 存在于无限集中,则将一个num添加 到该无限集中。
示例:
输入 ["SmallestInfiniteSet", "addBack", "popSmallest", "popSmallest", "popSmallest", "addBack", "popSmallest", "popSmallest", "popSmallest"] [[], [2], [], [], [], [1], [], [], []] 输出 [null, null, 1, 2, 3, null, 1, 4, 5]解释 SmallestInfiniteSet smallestInfiniteSet = new SmallestInfiniteSet(); smallestInfiniteSet.addBack(2); // 2 已经在集合中,所以不做任何变更。 smallestInfiniteSet.popSmallest(); // 返回 1 ,因为 1 是最小的整数,并将其从集合中移除。 smallestInfiniteSet.popSmallest(); // 返回 2 ,并将其从集合中移除。 smallestInfiniteSet.popSmallest(); // 返回 3 ,并将其从集合中移除。 smallestInfiniteSet.addBack(1); // 将 1 添加到该集合中。 smallestInfiniteSet.popSmallest(); // 返回 1 ,因为 1 在上一步中被添加到集合中,// 且 1 是最小的整数,并将其从集合中移除。 smallestInfiniteSet.popSmallest(); // 返回 4 ,并将其从集合中移除。 smallestInfiniteSet.popSmallest(); // 返回 5 ,并将其从集合中移除。
提示:
1 <= num <= 1000- 最多调用
popSmallest和addBack方法 共计1000次
二、题解
这题的关键点是始终要保证无限集合是连续的。无限集合的范围可以认为是从 1 到正无穷大,并且都是正整数。
这道我是用TreeSet和一个min变量来维护这个无限集合。为什么用TreeSet,因为TreeSet支持维护元素的自然顺序。
TreeSet:小于min的有序集合。
min:有序集合的最小值。
添加元素的时候分为两种情况:
-
添加元素的时候如果添加的值大于等于无限集合中的最小值
min,就不要添加,因为无限集合是连续的,添加的元素在无限集合中已经存在。(简单点说:比min还大的数不用加,说明已经存在了) -
添加的元素如果小于无限集合的最小值 min 也不能直接添加,如果贸然添加会导致无限集合不连续,只需要把它添加到有序集合 TreeSet 中即可, TreeSet 中存放的值都是小于 min 的。所以要加在TreeSet中,要靠TreeSet来维护。
删除元素的时候:
-
删除的时候先判断有序集合 TreeSet 是否为空,如果不为空,说明存在比 min 还小的元素,直接从 TreeSet 中删除。否则就从有序集合中删除 min ,删除之后 min 值要加 1 。
三、代码
class SmallestInfiniteSet {TreeSet<Integer> set = new TreeSet<>();int min = 1;public SmallestInfiniteSet() {}public int popSmallest() {if (set.isEmpty()) {return min++;//先返回,再++}return set.pollFirst();//弹出set的第一个元素,并删除}public void addBack(int num) {if (num < min) {//大于的话,说明存在了set.add(num);}}
}四、总结
使用TreeSet和min变量来维护一个无限集合,保证集合的连续性。添加元素时,若元素大于等于min,则不添加;若元素小于min,则将其添加到TreeSet中。删除元素时,先判断TreeSet是否为空,若不为空,则从TreeSet中删除元素;若为空,则将min值加1。该算法能够高效地添加和删除元素,并保持集合的连续性。
该算法还可以用优先队列(小根堆)+ hash表解题,比较优秀。
相关文章:

【数据结构和算法】无限集中的最小数字
其他系列文章导航 Java基础合集 设计模式合集 多线程合集 分布式合集 ES合集 文章目录 其他系列文章导航 文章目录 前言 一、题目描述 二、题解 三、代码 四、总结 前言 这是力扣的2336题,难度为中等,解题方案有很多种,本文讲解我认为…...
SimpleDataFormat 非线程安全
目录 前言 正文 1.出现异常 2.解决方法1 3.解决方法2 总结 前言 SimpleDateFormat 类是 Java 中处理日期和时间格式化和解析的类,但它并不是线程安全的。这意味着多个线程不能安全地共享一个 SimpleDateFormat 实例进行日期和时间的解析和格式化。当多个…...
SpringBoot : ch12 多模块配置YAML文件
前言 当您使用SpringBoot框架进行项目开发时,通常需要配置一些参数和属性。在实际开发中,可能需要将这些配置参数分成多个不同的YAML文件,并将它们组织到不同的模块中。这样可以方便管理和维护配置文件,并且可以避免配置文件的冲…...

TensorRT之LeNet5部署(onnx方式)
文章目录 前言LeNet-5部署1.ONNX文件导出2.TensorRT构建阶段(TensorRT模型文件)🧁创建Builder🍧创建Network🍭使用onnxparser构建网络🍬优化网络🍡序列化模型🍩释放资源 3.TensorRT运行时阶段(推理)&#x…...
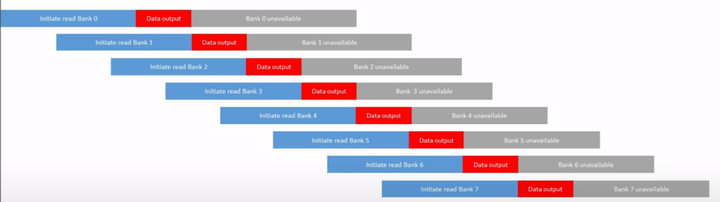
Xilinx FPGA平台DDR3设计详解(二):DDR SDRAM组成与工作过程
本文主要介绍一下DDR SDRAM的基本组成以及工作过程,方便大家更好的理解和掌握DDR的控制与读写。 一、DDR SDRAM的基本组成 1、SDRAM的基本单元 SDRAM的基本单元是一个CMOS晶体管和一个电容组成的电路。 晶体管最上面的一端,称作栅极,通过…...
 属性包装器详解)
ios(swiftui) 属性包装器详解
目录 1. State 2. Binding 3. ObservedObject 和Published 4. StateObject 5. EnvironmentObject和Environment 6. AppStorage 在 SwiftUI 中,属性包装器用于增强和管理视图的状态,以及处理视图与数据模型之间的绑定和交互。下面是一些常见…...
)
【智能家居】面向对象编程OOP和设计模式(工厂模式)
面向对象编程 类和对象 面向对象编程和面向过程编程区别 设计模式 软件设计模式按类型分 工厂模式 面向对象编程 面向对象编程(Object-Oriented Programming,OOP)是一种程序设计范式,其中程序被组织成对象的集合,每…...

Docker安装Memcached+Python调用
简介:Memcached是一个通用的分布式内存缓存系统。它通常用于通过在RAM中缓存数据和对象来加速动态数据库驱动的网站,以减少必须读取外部数据源(如数据库或API)的次数。Memcached的API提供了一个分布在多台机器上的非常大的哈希表。…...

网页开发 HTML
目录 HTML概述 HTML结构 HTML标签语法 基本标签 标题标签 换行标签 段落标签 文本格式化标签 特殊符号 div和span标签 超链接标签 锚点 img标签 列表标签 表格标签 表单标签 HTML概述 HTML,即超文本标记语言(HyperText Markup Language …...
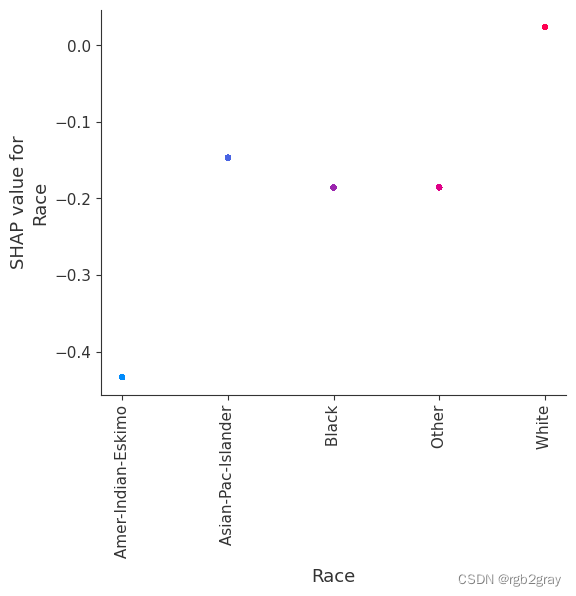
SHAP(五):使用 XGBoost 进行人口普查收入分类
SHAP(五):使用 XGBoost 进行人口普查收入分类 本笔记本演示了如何使用 XGBoost 预测个人年收入超过 5 万美元的概率。 它使用标准 UCI 成人收入数据集。 要下载此笔记本的副本,请访问 github。 XGBoost 等梯度增强机方法对于具有…...

LeetCode 8 字符串转整数
题目描述 字符串转换整数 (atoi) 请你来实现一个 myAtoi(string s) 函数,使其能将字符串转换成一个 32 位有符号整数(类似 C/C 中的 atoi 函数)。 函数 myAtoi(string s) 的算法如下: 读入字符串并丢弃无用的前导空格检查下一…...

前缀和 LeetCode1423. 可获得的最大点数
几张卡牌 排成一行,每张卡牌都有一个对应的点数。点数由整数数组 cardPoints 给出。 每次行动,你可以从行的开头或者末尾拿一张卡牌,最终你必须正好拿 k 张卡牌。 你的点数就是你拿到手中的所有卡牌的点数之和。 给你一个整数数组 cardPoi…...
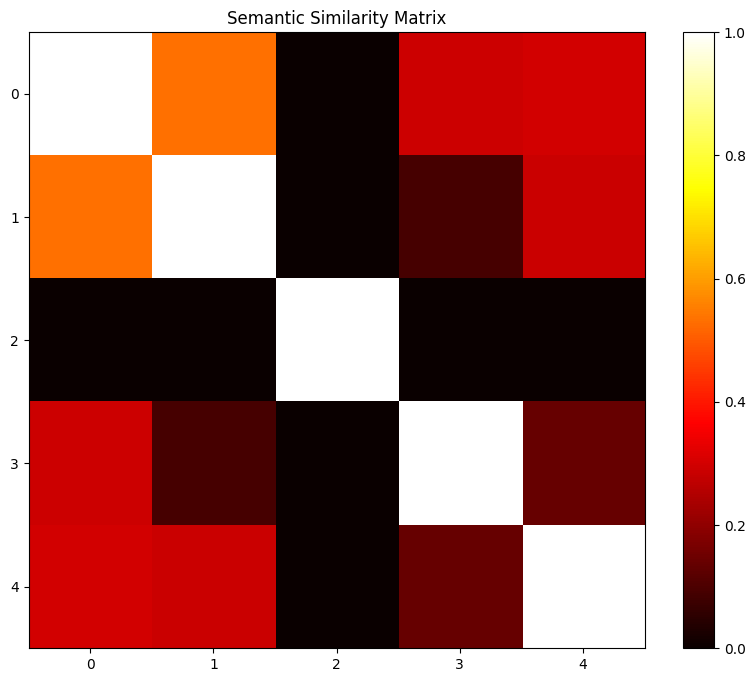
探索意义的深度:自然语言处理中的语义相似性
一、说明 语义相似度,反应出计算机对相同内容,不同表达的识别能力。因而识别范围至少是个句子,最大范围就是文章,其研究方法有所区别。本文将按照目前高手的研究成绩,作为谈资介绍给诸位。 二、语义相似度简介 自然语言…...

WT2605-24SS高品质录音语音芯片:实时输出、不保存本地,引领音频技术新潮流
随着科技的快速发展,高品质音频技术成为了现代社会不可或缺的一部分。在这个追求高品质、高效率的时代,唯创知音推出的WT2605-24SS高品质录音芯片,以其独特的功能和卓越的性能,引领着音频技术的新潮流。 首先,WT2605-…...

Git 合并冲突解决步骤
Git 合并冲突解决步骤 1. 找到并打开冲突文件 定位到发生冲突的文件。可以通过 Git 的命令行输出找到这些文件。例如: pom.xmlsrc/main/java/com/zzm/config/SecurityConfig.javasrc/main/java/com/zzm/service/chat/UserConversationsServiceImpl.javasrc/main/…...
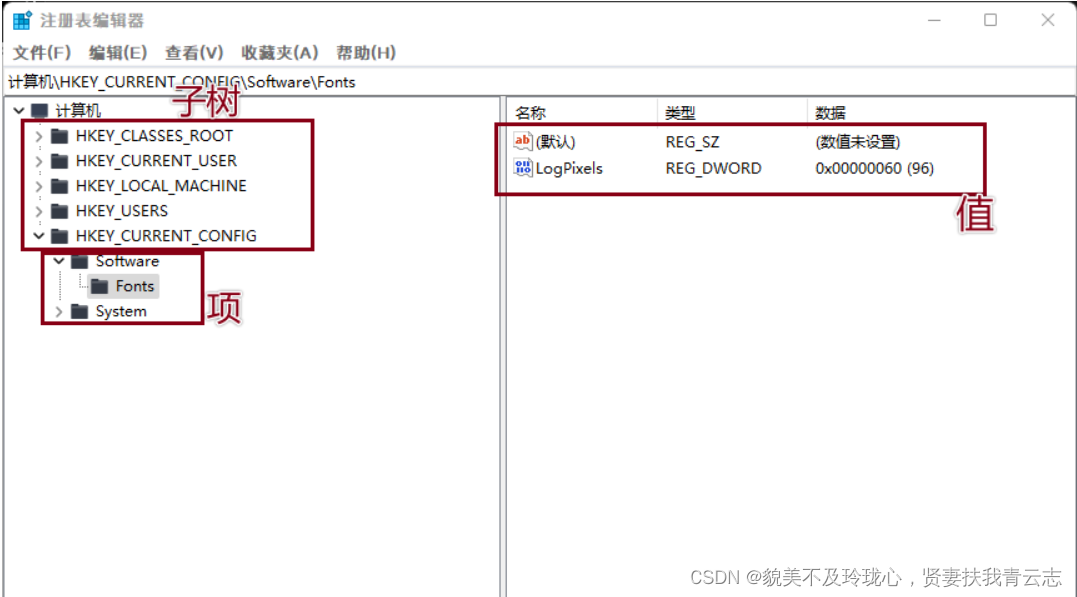
Windows核心编程 注册表
目录 注册表概述 打开关闭注册表 创建删除子健 查询写入删除键值 子健和键值的枚举 常用注册表操作 注册表概述 注册表是Windows操作系统、硬件设备以及客户应用程序得以正常运行和保存设置的核心"数据库",也可以说是一个非常巨大的树状分层结构的…...
【算法专题】二分查找
二分查找 二分查找1. 二分查找2. 在排序数组中查找元素的第一和最后一个位置3. 搜索插入位置4. x 的平方根5. 山脉数组的峰顶索引6. 寻找峰值7. 寻找旋转排序数组中的最小值8. 点名 二分查找 1. 二分查找 题目链接 -> Leetcode -704.二分查找 Leetcode -704.二分查找 题…...

中国消费电子行业发展趋势及消费者需求洞察|徐礼昭
一、引言 近年来,随着科技的飞速发展,消费电子行业面临着前所未有的挑战与机遇。本文将从行业发展趋势、消费者需求洞察以及企业数字化转型的方向和动作三个方面,对消费电子行业进行深入剖析。 二、消费电子行业发展趋势 5G技术的普及和应…...
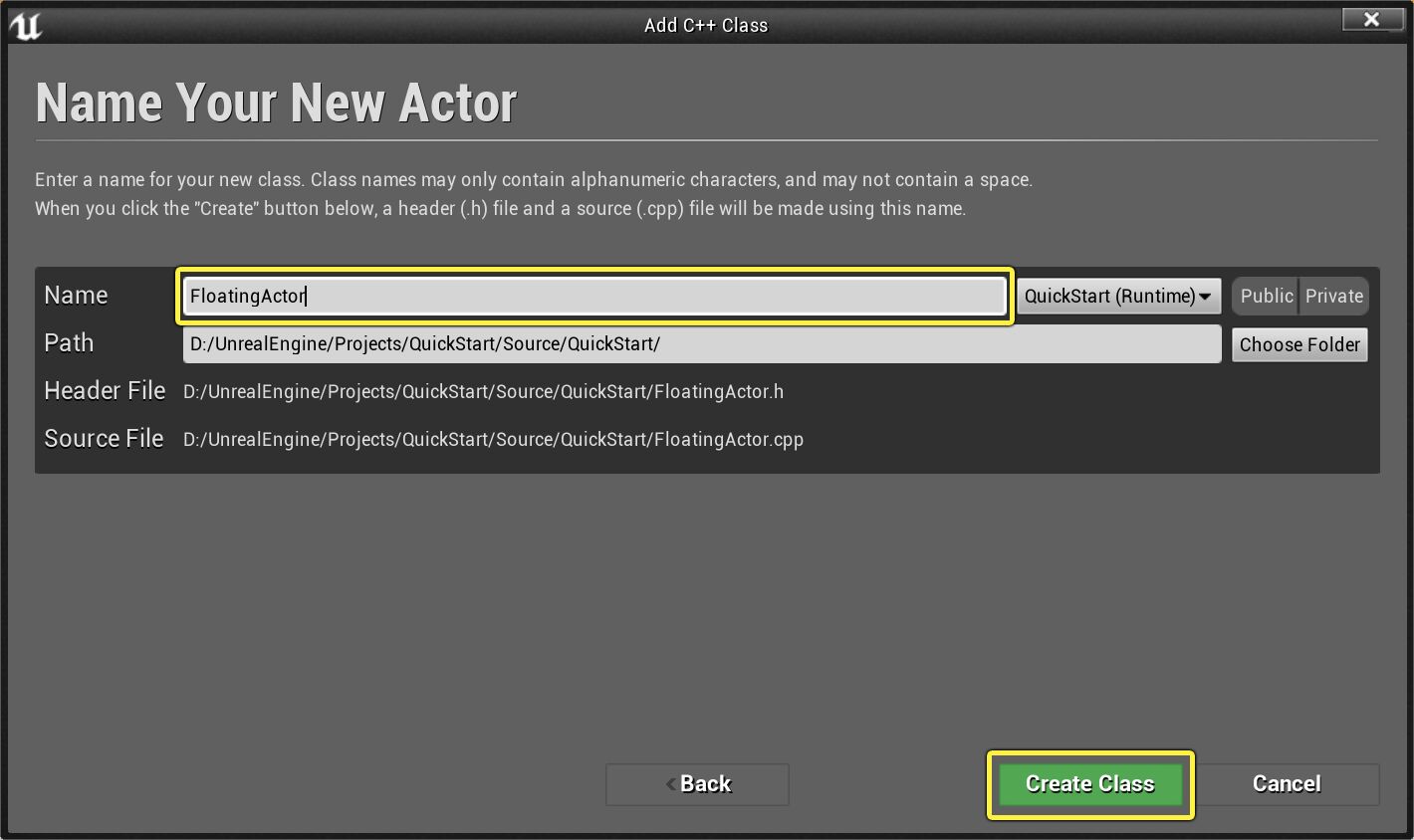
UE学习C++(1)创建actor
创建新C类 在 虚幻编辑器 中,点击 文件(File) 下拉菜单,然后选择 新建C类...(New C Class...) 命令: 此时将显示 选择父类(Choose Parent Class) 菜单。可以选择要扩展的…...

【CTA认证】Android8实现android6以下的应用运行时也要申请权限
需求 CTA入网认证,要求低版本比如Android6以下的应用,运行时,也需要有运行时权限(Runtime Permission)功能,不能默认就取到权限,必须人工在设置中打开才可。 环境 Android 8 实现 frameworks 修改思路是所有APP都…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...
