Python函数的高级用法

Python 的函数是“一等公民”,因此函数本身也是一个对象,函数既可用于赋值,也可用作其他函数的参数,还可作为其他函数的返回值。
使用函数变量
Python 的函数也是一种值:所有函数都是 function 对象,这意味着可以把函数本身赋值给变量,就像把整数、浮点数、列表、元组赋值给变量一样。
当把函数赋值给变量之后,接下来程序也可通过该变量来调用函数。例如如下代码:
# 定义一个计算乘方的函数 def pow(base, exponent) :result = 1for i in range(1, exponent + 1) :result *= basereturn result # 将pow函数赋值给my_fun,则my_fun可当成pow使用 my_fun = pow print(my_fun(3 , 4)) # 输出81 # 定义一个计算面积的函数 def area(width, height) :return width * height # 将area函数赋值给my_fun,则my_fun可当成area使用 my_fun = area print(my_fun(3, 4)) # 输出12
从上面代码可以看出,程序依次将 pow()、area() 函数赋值给 my_fun 变量,接下来即可通过 my_fun 变量分别调用 pow()、area() 函数。
其实 python 已经内置了计算乘方的方法,因此此处的 pow() 函数并没有太大的实际意义,只是作为示范使用。
通过对 my_fun 变量赋值不同的函数,可以让 my_fun 在不同的时间指向不同的函数,从而让程序更加灵活。由此可见,使用函数变量的好处是让程序更加灵活。
除此之外,程序还可使用函数作为另一个函数的形参和(或)返回值。
使用函数作为函数形参
有时候需要定义一个函数,该函数的大部分计算逻辑都能确定,但某些处理逻辑暂时无法确定,这意昧着某些程序代码需要动态改变,如果希望调用函数时能动态传入这些代码,那么就需要在函数中定义函数形参,这样即可在调用该函数时传入不同的函数作为参数,从而动态改变这段代码。
Python 支持像使用其他参数一样使用函数参数,例如如下程序:
# 定义函数类型的形参,其中fn是一个函数
def map(data, fn) : result = []# 遍历data列表中每个元素,并用fn函数对每个元素进行计算# 然后将计算结果作为新数组的元素for e in data :result.append(fn(e))return result
# 定义一个计算平方的函数
def square(n) :return n * n
# 定义一个计算立方的函数
def cube(n) :return n * n * n
# 定义一个计算阶乘的函数
def factorial(n) :result = 1for index in range(2, n + 1) :result *= indexreturn result
data = [3 , 4 , 9 , 5, 8]
print("原数据: ", data)
# 下面程序代码3次调用map()函数,每次调用时传入不同的函数
print("计算数组元素的平方")
print(map(data , square))
print("计算数组元素的立方")
print(map(data , cube))
print("计算数组元素的阶乘")
print(map(data , factorial))
上面程序中定义了一个 map() 函数,该函数的第二个参数是一个函数类型的参数,这意味着每次调用函数时可以动态传入一个函数,随着实际传入函数的改变,就可以动态改变 map() 函数中的部分计算代码。
接下来的三行粗体字代码调用了 map() 函数三次,三次调用依次传入了 square、cube、factorial 函数作为参数,这样每次调用 map() 函数时实际的执行代码是有区别的。
编译、运行上面程序,可以看到如下输出结果:
原数据: [3, 4, 9, 5, 8] 计算数组元素的平方 [9, 16, 81, 25, 64] 计算数组元素的立方 [27, 64, 729, 125, 512] 计算数组元素的阶乘 [6, 24, 362880, 120, 40320]
使用函数作为返回值
前面己经提到,Python 还支持使用函数作为其他函数的返回值。例如如下程序:
def get_math_func(type) :# 定义一个计算平方的局部函数def square(n) : # ①return n * n# 定义一个计算立方的局部函数def cube(n) : # ②return n * n * n# 定义一个计算阶乘的局部函数def factorial(n) : # ③result = 1for index in range(2 , n + 1):result *= indexreturn result# 返回局部函数if type == "square" :return squareif type == "cube" :return cubeelse:return factorial
# 调用get_math_func(),程序返回一个嵌套函数
math_func = get_math_func("cube") # 得到cube函数
print(math_func(5)) # 输出125
math_func = get_math_func("square") # 得到square函数
print(math_func(5)) # 输出25
math_func = get_math_func("other") # 得到factorial函数
print(math_func(5)) # 输出120
程序中,定义了一个 get_math_func() 函数,该函数将返回另一个函数。接下来在 get_math_func() 函数体内的 ①、②、③ 号粗体字代码分别定义了三个局部函数,最后 get_math_func() 函数会根据所传入的参数,使用这三个局部函数之一作为返回值。
相关文章:

Python函数的高级用法
Python 的函数是“一等公民”,因此函数本身也是一个对象,函数既可用于赋值,也可用作其他函数的参数,还可作为其他函数的返回值。 使用函数变量 Python 的函数也是一种值:所有函数都是 function 对象,这意…...
excel单元格内换行按什么快捷键
如果我们使用excel软件的时候,因为一些日常的操作太过繁琐想要简化自己的操作步骤的话,其实是有很多快捷方式在其中的。那么对excel单元格内换行按什么快捷键这个问题,据小编所知我们可以在表格中使用Alt Enter来进行换行。详细内容就来看下…...
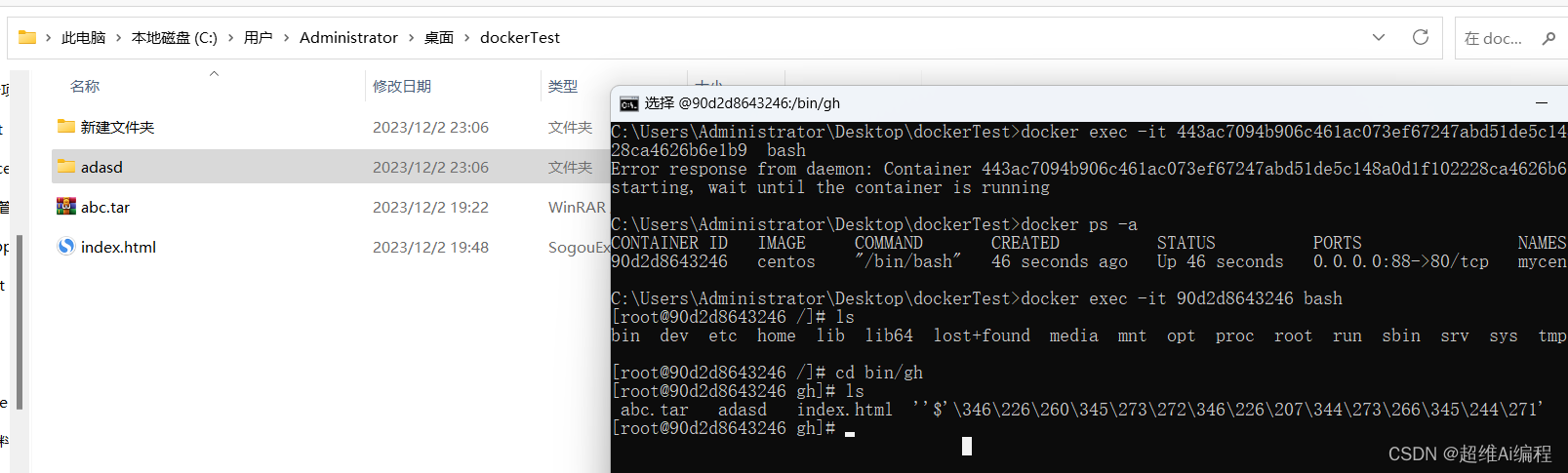
docker容器内部文件挂载主机
docker images执行该命令可以发现一个centos镜像 docker run --namemycentos -itd --privilegedtrue --restartalways -p 88:80 -v C:\Users\Administrator\Desktop\dockerTest:/bin/gh:ro centosdocker run 命令用于在 Docker 上创建和运行容器。 --namemycentos 指定容器…...

python 实现一个简单的计算器
python 实现一个简单的计算器 本文主要整合下tkinter ,实现下简单的计算器. 代码如下: #!/usr/bin/python3 # -*- coding: UTF-8 -*- """Author: zhTime 2023/12/2 下午13:01 .Email:Describe: """ import tkinter as tk# 创建计算器窗口 ro…...

前端对浏览器的理解
浏览器的主要构成 用户界面 - 包括地址栏、后退/前进按钮、书签目录等,也就是你所看到的除了用来显示你所请求页面的主窗口之外的其他部分。 浏览器引擎 - 用来查询及操作渲染引擎的接口。 渲染引擎 - 用来显示请求的内容&#…...
:X509_verify通过ca证书的public key验证证书的签名)
Linux(openssl):X509_verify通过ca证书的public key验证证书的签名
/docs/man3.0/man3/X509_verify.html (openssl.org) 提供了方法用于通过ca证书的public key验证证书的签名 //verify_cert.hpp #include <string> #include <memory> #include <filesystem> #include <openssl/pem.h>using namespace std; namespace …...
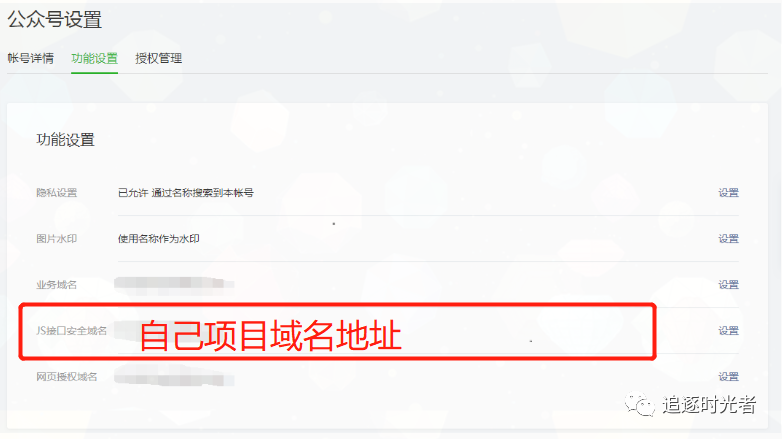
全面的.NET微信网页开发之JS-SDK使用步骤、配置信息和接口请求签名生成详解
JSSDK使用步骤 步骤一:绑定安全域名: 先登录微信公众平台进入“公众号设置”的“功能设置”里填写“JS接口安全域名”。 步骤二:引入JS文件: 在需要调用JS接口的页面引入如下JS文件,(支持https):http://…...

深入了解汉字转拼音转换工具:原理与应用
一、引言 汉字作为世界上最古老、最具象形意的文字之一,承载了数千年的历史文明。然而,在现代信息技术环境下,汉字的输入、输出和检索等方面存在一定的局限性。拼音作为汉字的一种音标表达方式,能够有效地解决这些问题。本文将为…...
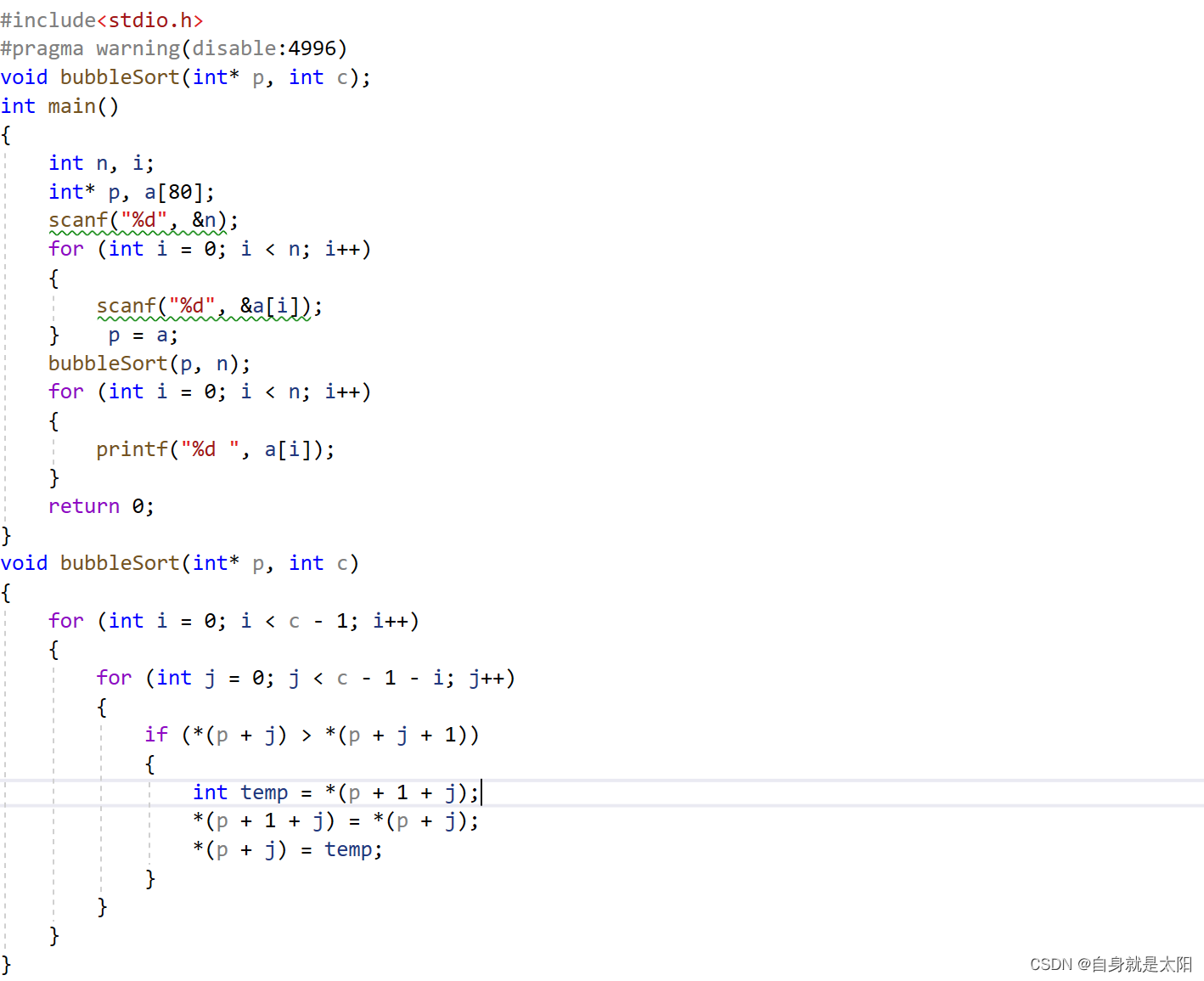
沈阳师范大学期末考试复习pta循环数组函数指针经典编程题汇总+代码分析
目录 前言:临近期末,接下来给大家分享一些经典的编程题,方便大家复习。不一定难,但都是入门的好题,尽可能的吃透彻。因为据说期末考试的题很多来自pta上面的原题。 对于一些语言我是用c来写的,不妨碍理解…...

【面试攻略】Oracle中blob和clob的区别及查询修改方法
大家好,我是小米,欢迎来到小米的技术小屋!今天我们要一起来聊聊一个在面试中常常被问到的问题——“Oracle中Blob和Clob有啥区别,在代码中怎么查询和修改这两个类型的字段里的内容?”别急,跟着小米一步步揭…...
An illegal reflective access operation has occurred问题记录
报错 2023-11-30T01:08:18.7440800 [ERROR] [system.err] WARNING: An illegal reflective access operation has occurred 2023-11-30T01:08:18.7450800 [ERROR] [system.err] WARNING: Illegal reflective access by com.intellij.ui.JreHiDpiUtil to method sun.java2d.Sun…...
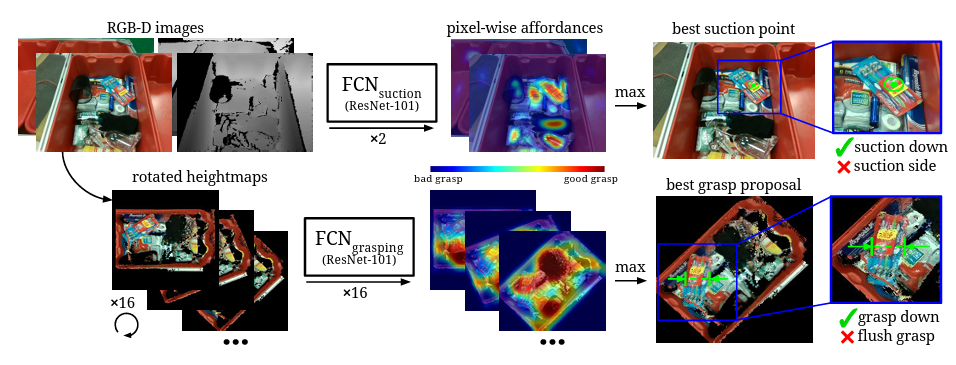
抓取检测(Grasp Dection)
抓取检测 抓取检测被定义为能够识别任何给定图像中物体的抓取点或抓取姿势。抓取策略应确保对新物体的稳定性、任务兼容性和适应性,抓取质量可通过物体上接触点的位置和手的配置来测量。为了掌握一个新的对象,完成以下任务,有分析方法和经验…...

人工智能学习4(特征选择)
编译工具:PyCharm 有些编译工具在绘图的时候不需要写plt.show()或者是print就可以显示绘图结果或者是显示打印结果,pycharm需要(matplotlib.pyplot) 文章目录 编译工具:PyCharm 特征选择嵌入法特征选择练习ÿ…...

vue中keep-alive的使用
什么是keep-alive? keep-alive是一个内置组件,用于缓存和管理组件的状态。 当 keep-alive包裹一个组件时,这个组件的状态将会被缓存起来,而不是每次重新渲染。这在多个视图之间切换时特别有用,可以避免重复的创建和销…...

2023年第十二届数学建模国际赛小美赛B题工业表面缺陷检测求解分析
2023年第十二届数学建模国际赛小美赛 B题 工业表面缺陷检测 原题再现: 金属或塑料制品的表面缺陷不仅影响产品的外观,还可能对产品的性能或耐久性造成严重损害。自动表面异常检测已经成为一个有趣而有前景的研究领域,对视觉检测的应用领域有…...

2023全球数字贸易大赛-web3,区块链,诺威信,浪潮云,微众区块链,福建中科星泰,瓴羊区块链,联想-元宇宙,硅基智能-
目录 诺威信B隐私计算平台 浪潮云=星火连-澳优码 HyperChain 产品介绍...

计算机网络一:TCP/IP基础概念和常见面试题
TCP/IP是一种网络通信协议族,它由两个主要的协议构成:TCP(传输控制协议)和IP(网络互联协议)。TCP负责数据的可靠传输,而IP则负责数据的路由和转发。 TCP/IP有哪些层次结构?每个层次的…...

图论|684.冗余连接 685. 冗余连接 II
684.冗余连接 题目:树可以看成是一个连通且 无环 的 无向 图。 给定往一棵 n 个节点 (节点值 1~n) 的树中添加一条边后的图。添加的边的两个顶点包含在 1 到 n 中间,且这条附加的边不属于树中已存在的边。图的信息记录于长度为 n 的二维数组 …...
依据小兔鲜项目,总结Javascript数组常用方法
find 在向购物车添加某种规格的商品时,查找购物车列表中是否已经存在该规格的商品 find()方法传入一个回调函数,代表对数组每一项item的校验要求 返回数组中第一个符合条件的元素的值,如果没有则返回undefined const item cartList.value…...
制作飞腾(arm)芯片架构的nexus镜像
nexus官方没有arm架构的镜像,下面介绍一种自己制作镜像的方式 1、事先准备 在一个arm架构机器上安装docker下载nexus的linux版(https://www.sonatype.com/download-oss-sonatype)下载centos的arm架构镜像(docker pull centos-centos8.4.2105)下载arm版本的java8(ht…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...
