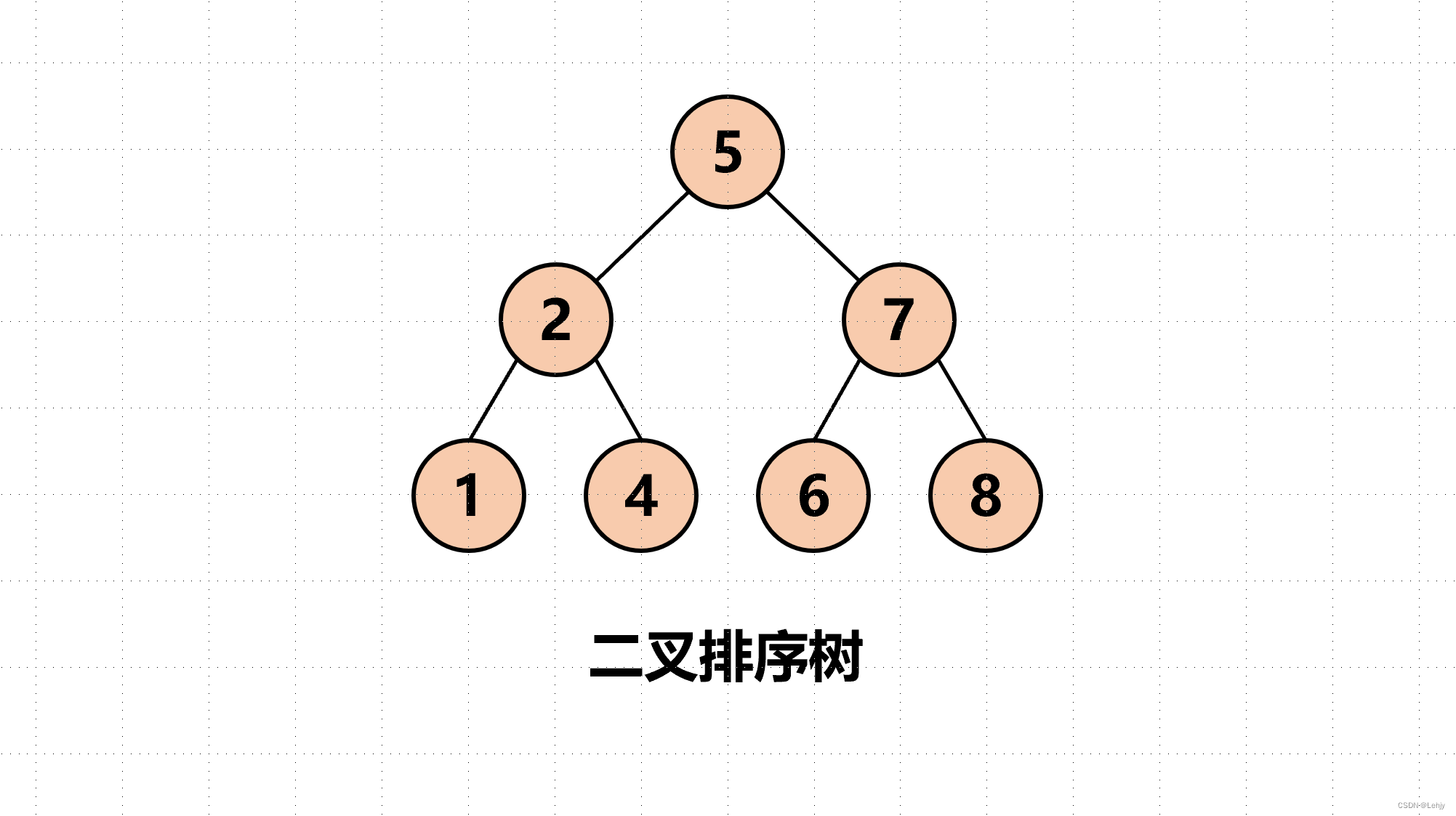
【数据结构】——二叉树特点
前言:我们前面已经了解了二叉树的一些概念,那么我们今天就来了解下二叉树的遍历实现和一些性质。
二叉树的遍历方式有三种:前序,中序,后序。
前序:先根节点,再左子树,最后右子树。
中序:先左子树,再根节点,最后右子树。
后序:先左子树,再右子树,最后根节点。
前序遍历:
void PrevOrder(TreeNode* root)
{if (root == NULL){printf("N ");return;}printf("%d ", root->data);PrevOrder(root->left);PrevOrder(root->right);
}
如果我们的根节点为空就返回空,不为空就递归左子树,如果左子树为空就返回递归访问右子树。
中序遍历:
void InOrder(TreeNode* root)
{if (root == NULL){printf("N");return;}InOrder(root->left);printf("%d ", root->data);InOrder(root->right);
}
先访问遍历左子树,再根节点,最后在访问右子树。
后序遍历:
void Tailorder(TreeNode* root)
{if (root == NULL){printf("N");return;}Tailorder(root->left);Tailorder(root->right);printf("%d", root->data);
}
先遍历左子树,再遍历右子树,最后在根节点。
求二叉树节点个数:
int TreeSize(TreeNode* root)
{return root == NULL ? 0 :TreeSize(root->left) +TreeSize(root->right) + 1;
}
我们递归实现,左子树的节点个数加上右子树的节点个数再加上根节点的个数就是节点的总个数。
求叶子结点的个数:
int TreeLeafSize(TreeNode* root)
{// 空 返回0if (root == NULL)return 0;// 不是空,是叶子 返回1if (root->left == NULL&& root->right == NULL)return 1;// 不是空 也不是叶子 分治=左右子树叶子之和return TreeLeafSize(root->left) +TreeLeafSize(root->right);
}求二叉树的高度:
int TreeHeight(TreeNode* root)
{if (root == NULL)return 0;int leftHeight = TreeHeight(root->left);int rightHeight = TreeHeight(root->right);return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
}
因为我们的递归结合上三目操作符会使得非常的复杂,所以我们用一个数据来保存左右子树的高度,我们的二叉树的高度为左右子树较高的那个子树加上1,所以我们返回的是左右子树高度更高的再加上1就是二叉树的高度。
我们的代码还可以进行改进,我们C语言的fmax函数:该函数的作用是比较两个数得到较大的那一个数
int TreeHeight(TreeNode* root)
{if (root == NULL)return 0;return fmax(TreeHeight(root->left), TreeHeight(root->right)) + 1;
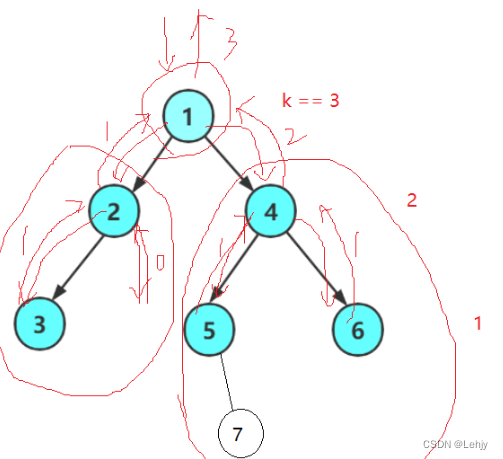
}求二叉树第k层节点个数:
int TreeLevelK(TreeNode* root, int k)
{assert(k > 0);if (root == NULL)return 0;if (k == 1)return 1;return TreeLevelK(root->left, k - 1)+ TreeLevelK(root->right, k - 1);
}
第k层的节点等于第k-1层的节点数相加。
现在我们要求第三层的节点数,相当于我们返回它的第二层,而我们的第二层节点数要返回我们的第一层节点数,我们的左子树返回一个节点,右子树返回两个节点,所以就是三个节点。
如果对大家有所帮助的话就支持一下吧!
相关文章:
【数据结构】——二叉树特点
前言:我们前面已经了解了二叉树的一些概念,那么我们今天就来了解下二叉树的遍历实现和一些性质。 二叉树的遍历方式有三种:前序,中序,后序。 前序:先根节点,再左子树,最后右子树。 中…...
C++的类和对象(一)
目录 1、面向过程和面向对象初认识 2、为什么要有类 3、类的定义 类的两种定义方式 4、类的访问限定符 5、类的作用域 5.1 为什么要有作用域? 5.2类作用域 6、类的实例化 6.1类的实例化的定义 6.2类的实例化的实现 6.3经典面试题 7、类对象 7.1类对…...

基于单片机自动饮料混合机控制系统设计
**单片机设计介绍,基于单片机自动饮料混合机控制系统设计 文章目录 一 概要二、功能设计设计思路 三、 软件设计原理图 五、 程序六、 文章目录 一 概要 基于单片机自动饮料混合机控制系统设计是一个涉及多个领域的复杂项目,包括单片机技术、传感器技术…...
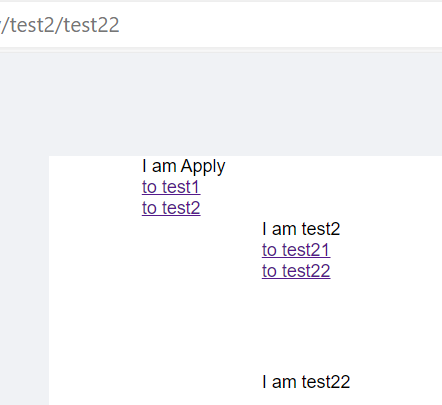
react-route-dom 实现简单的嵌套路由
最终效果 点击 to test1 点击to test2 > to test21 点击to test2 > to test22 代码如下 path: "page",element: <父组件 />,children: [{ path: "test1", element: <Test1 /> },{path: "test2",element: <Test2 />…...

万界星空科技灯具行业MES介绍
中国是LED照明产品最大的生产制造国,如今,我国初步形成了包括LED外延片的生产、LED芯片的制备、LED芯片的封装以及LED产品应用在内的较为完超为产业链,随着LED照明市场渗诱率的快速警升,LED下游应用市场将会越来越广阔。这也将推动…...

16进制字符串转字符串
一、浏览器上 function hexToUtf8(hexString) {const hexArray hexString.match(/.{1,2}/g) || [];const uint8Array new Uint8Array(hexArray.map(hex > parseInt(hex, 16)));const textDecoder new TextDecoder(GB2312); //可以切换字符编码return textDecoder.decode…...

pymysql.err.InternalError: (1054, “Unknown column ‘nan‘ in ‘field list‘“
记录在本地环境通过,然后在云环境,解决问题的过程; 最近两天遇到一个bug,具体就是在本地Pyhon环境运行成功,但是当放在云服务跑的时候,去屡屡报错,具体报错信息如下: pymysql.err.I…...

SQL 错误 [1476] [22012]: ORA-01476: 除数为 0
Oracle sql 语句 添加判断,如果分母为0,则查询结果为0,如果分母不为0,则返回查询结果 你可以使用条件表达式来实现这个要求。以下是一个示例的Oracle SQL查询语句,其中添加了判断条件来处理分母为0的情况:…...

go语言项目的目录结构
Golang 的项目目录结构并没有一个强制的标准,但社区中形成了一些共识和最佳实践,以便更好地组织和管理代码。以下是一个典型的 Golang 项目目录结构示例: /myproject ├── /cmd | ├── /app | | └── main.go | …...

Android : DataBinding 简化开发 简单应用
1.导包 ViewModel 用于观察数据 // 使用androidx版本库 ViewModelProviders implementation androidx.lifecycle:lifecycle-extensions:2.1.0-alpha032.在build.gradle 添加 在android 代码块中添加 复制后点更新(Sync Now) android{...// 步骤1.开启…...
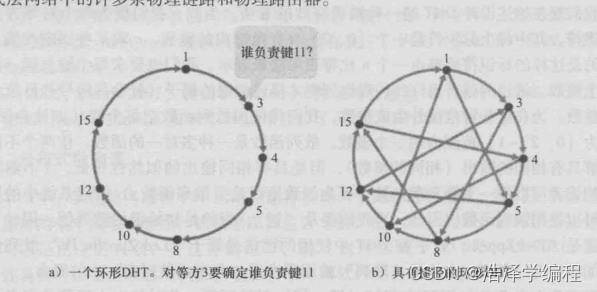
计算机网络:应用层(下篇)
文章目录 前言一 、电子邮件(Email)1.邮件服务器2.SMTP[RFC 2821]3.邮件报文格式4.邮件访问协议 二、DNS(域名系统)1.DNS的历史2.DNS总体思路和目标(1)问题1:DNS名字空间(2ÿ…...
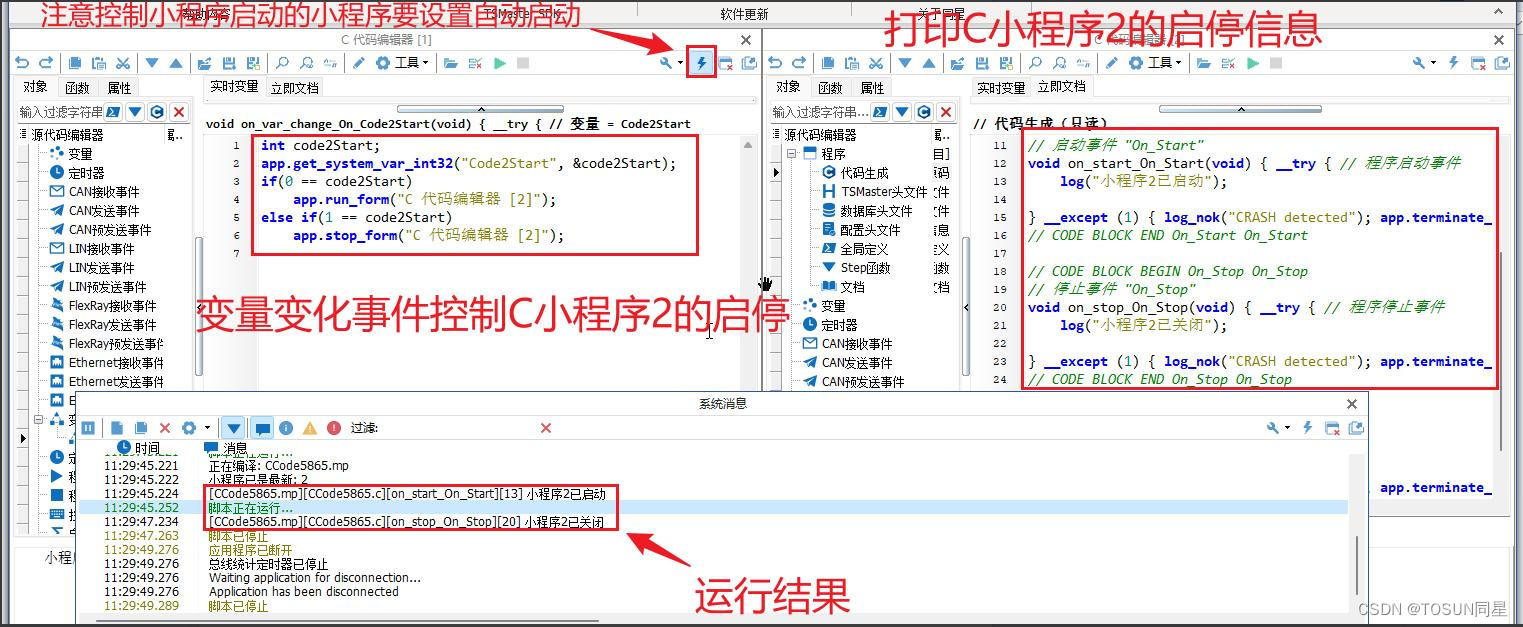
干货分享 | TSMaster小程序启动和停止的自动化控制流程
在实际应用场景中,用户常常需要按一定逻辑和时序来控制TSMaster内置功能模块的启动和停止,TSMaster软件内置有C/Python小程序和图形程序,开发者可以通过编程对这些模块的运行进行精确控制。本文将重点和大家分享一下如何通过C代码来控制TSMas…...

AI视频智能分析识别技术的发展与EasyCVR智慧安防视频监控方案
随着科技的不断进步,基于AI神经网络的视频智能分析技术已经成为了当今社会的一个重要组成部分。这项技术通过利用计算机视觉和深度学习等技术,实现对视频数据的智能分析和处理,从而为各个领域提供了广泛的应用。今天我们就来介绍下视频智能分…...

外包干了2个月,技术倒退2年。。。
先说一下自己的情况,本科生,20年通过校招进入深圳某软件公司,干了接近4年的功能测试,今年国庆,感觉自己不能够在这样下去了,长时间呆在一个舒适的环境会让一个人堕落!而我已经在一个企业干了四年的功能测试…...
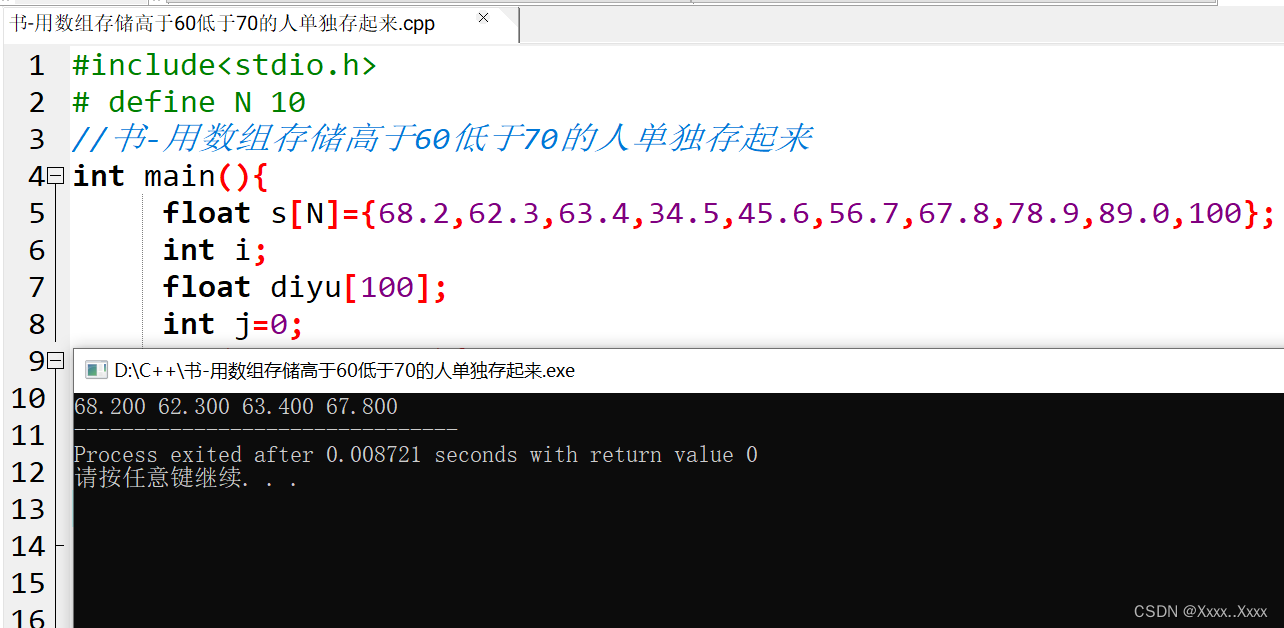
书-用数组存储高于60低于70的人单独存起来
#include<stdio.h> # define N 10 //书-用数组存储高于60低于70的人单独存起来 int main(){float s[N]{68.2,62.3,63.4,34.5,45.6,56.7,67.8,78.9,89.0,100};int i;float diyu[100];int j0;for(i0;i<N;i){if(s[i]>60 && s[i]<70)diyu[j]s[i];//这里的范…...

三、DVP摄像头调试笔记(图片成像质量微调整,非ISP)
说明:当前调试仅仅用来测试和熟悉部分摄像头寄存器模式 一、图片成像方向控制,基本每个摄像头都会有上下左右翻转寄存器 正向图片 反向图片 二、设置成像数据成各种颜色,(黑白/原彩/黄色等等) 在寄存器书册描述中…...

Linux--程序地址空间
📘北尘_:个人主页 🌎个人专栏:《Linux操作系统》《经典算法试题 》《C》 《数据结构与算法》 ☀️走在路上,不忘来时的初心 [TOC](文章目录) 一、程序地址空间回顾 我们在讲C语言的时候,老师给大家画过这样的空间布局…...

【超全】React学习笔记 下:路由与Redux状态管理
React学习笔记 React系列笔记学习 上篇笔记地址:【超全】React学习笔记 上:基础使用与脚手架 中篇笔记地址:【超全】React学习笔记 中:进阶语法与原理机制 React路由概念与理解使用 1. 引入 React路由是构建单页面应用(SPA, Sin…...
matplotlib学习
显示两个figure 坐标上刻度修改 plt.xlim() 下标范围 plt.xticks() 替换新的下标 图例显示 散点图 subplot多合一显示...

【网络安全】-安全常见术语介绍
文章目录 介绍1. 防火墙(Firewall)定义通俗解释 2. 恶意软件(Malware)定义通俗解释 3. 加密(Encryption)定义通俗解释 4. 多因素认证(Multi-Factor Authentication,MFA)定…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...

Python 高效图像帧提取与视频编码:实战指南
Python 高效图像帧提取与视频编码:实战指南 在音视频处理领域,图像帧提取与视频编码是基础但极具挑战性的任务。Python 结合强大的第三方库(如 OpenCV、FFmpeg、PyAV),可以高效处理视频流,实现快速帧提取、压缩编码等关键功能。本文将深入介绍如何优化这些流程,提高处理…...

沙箱虚拟化技术虚拟机容器之间的关系详解
问题 沙箱、虚拟化、容器三者分开一一介绍的话我知道他们各自都是什么东西,但是如果把三者放在一起,它们之间到底什么关系?又有什么联系呢?我不是很明白!!! 就比如说: 沙箱&#…...