西工大计算机学院计算机系统基础实验一(函数编写1~10)
还是那句话,千万不要慌,千万不要着急,耐下性子慢慢来,一步一个脚印,把基础打的牢牢的,一样不比那些人差。回到实验本身,自从按照西工大计算机学院计算机系统基础实验一(环境配置)-CSDN博客 这篇博客结束完成虚拟机平台VMware 17 Workstation Pro的安装,以及Ubuntu虚拟机的导入,还有实验包的导入之后,我们看到了如下图所示的实验压缩包content_1701767947881.tar,如 图1:查看被导入到Ubuntu虚拟机的实验包的压缩包content_1701767947881.tar 所示。接着我们解压缩这个包,如 图2:解压缩实验压缩包content_1701767947881.tar 所示。

(图1:查看被导入到Ubuntu虚拟机的实验包的压缩包content_1701767947881.tar)
(图2:解压缩实验压缩包content_1701767947881.tar。使用"tar xvf content_1701767947881.tar"命令解压实验压缩包之后,得到了lab1-handout文件夹)
接着进入到lab1-handout文件夹,并且查看该lab1-handout文件夹下有什么文件,如 图3:进入lab1-handout文件夹,查看该文件夹下的文件 所示。 但是千万不要急着,什么都不懂就开始做,先耐下性子来慢慢读一读README文件,了解清楚lab1-handout这个文件夹是用来干什么的,如 图4:使用less命令查看README文件 、图5:查看README文件的第一页、图6:查看README文件的第二页 所示。这其中可能有很多大家不熟悉的命令,但千万不要排斥它,跟着作者一步一步来就可以。

(图3:进入lab1-handout文件夹,查看该文件夹下的文件)
(图4:使用less命令查看README文件)
 (图5:查看README文件的第一页)
(图5:查看README文件的第一页)

(图6:查看README文件的第二页)
在这里不要害怕怎么读,不要害怕说因为它是英文,所以就感到害怕。不要害怕,耐下性子慢慢读,就可以读出来一二的。在这里它的大概意思是,我们需要编写bits.c文件中的几个函数的函数体,接着使用dlc可执行文件检查bits.c文件中我们所写的函数是否满足运算符等的要求,然后使用make clean命令清除掉上一次已生成的可执行文件,再使用make btest文件生成可执行文件,最后运行生成的可执行文件价差我们所写的函数的正确性。你可能听不懂这段话是什么意思,不要怕,你跟着作者做,后面都会详细的讲到的。接着使用同样的方法,我们来查看bits.c文件,如 图7:查看bits.c文件(上)、图8:查看bits.c文件(下) 所示。

(图7:查看bits.c文件(上))
 (图8:查看bits.c文件(下))
(图8:查看bits.c文件(下))
bits.c文件开头的一大段注释给我们三个要点信息:
要点1:不要使用"#include <stdio.h>",我们可以得到要点2与要点3:
要点2:对于整型数,只能使用& ^ | + << >> ! ~这八个运算符,只能定义并使用int型的局部变量以及函数参数变量,只能使用0x0到0xFF的int型常量;
要点3:对于浮点数,只能使用& ^ | + << >> ! ~这八个运算符,可以定义并使用int型或unsigned int型的局部变量以及函数参数变量,可以使用任意有符号整型与无符号整型常量,可以使用循环与条件判断。
大家记住它就好,不要深究,考虑到有些同学的Ubuntu没有内置VS code,而且vim编辑器对于初学者来说难度也有点大,所以我们选择Ubuntu内置的文本编辑器,开始编辑bits.c中的第一个函数,如 图9:使用Ubuntu内置的文本编辑器,开始编辑bits.c中的第1个函数 所示。如果文本编辑器的大小过小,可以按照 图10:调大文本编辑器显示文字的大小(上) 、图11:调大文本编辑器显示文字的大小(下) 所示。

(图9:使用Ubuntu内置的文本编辑器,开始编辑bits.c中的第1个函数)
 (图10:调大文本编辑器显示文字的大小(上))
(图10:调大文本编辑器显示文字的大小(上))
(图11:调大文本编辑器显示文字的大小(下))
定位到第174行,我们开始编写第一个函数bitXor,如 图12:定位到第174行,开始编写第1个函数bitXor 所示。

(图12:定位到第174行,开始编写第1个函数bitXor)
bitXor的意思是什么呢?意思是,需要我们只使用取反和位与运算,来实现异或操作。即只使用~与&,来实现^操作。那么该怎么实现这个功能呢?根据异或操作的定义,相同为0,不同才为1。也就是说,0^0=0,0^1=1,1^0=1,1^1=0。观察这个例子,我们发现,只要其中有并且只有1个为1即可。即~x&y和x&~y一个需要为1,一个需要为0,可以写成(~x&y)|(x&~y),但是不允许使用位或操作,那么我们应该怎么做呢?再思考下去就很麻烦了。我们不妨换一种思路,当x&y与~x&~y都为0时,这时只对应着两种情况,0^1=1与1^0=1,然后对x&y和~x&~y取反,得到~(x&y)和~(~x&~y),这时只有当0^1=1与1^0=1这两种情况下,~(x&y)和~(~x&~y)才都为1,进而~(x&y)&~(~x&~y)才为1,所以只需要写一个语句 "return ~(x&y)&~(~x&~y)"即可。如 图13:编写完成第1个函数bitXor 所示。接着保存对bits.c文件的修改,然后在包含bits.c文件的文件夹中打开命令行,如 图14:在包含bits.c文件的文件夹中打开命令行 所示。接着使用命令"./dlc -e bits.c"查看运算符的数量是否满足要求以及是否满足其它的要求。如果除了对各个函数所使用到的运算符进行计数之后就没有其它的输出,那么表明满足运算符和其它的要求。接着使用"make clean"命令清除掉上一次遗留的旧的文件,如 图15:使用命令"./dlc -e bits.c"和命令"make clean" 所示。接着再使用命令"make btest"生成新的文件,生成btest这个新的可执行文件之后,使用命令“./btest -f bitXor”来检验我们所写的第一个函数bitXor的正确性,其中"-f"选项制定了需要被检验的函数名,在这里需要被检验的函数名是bitXor。如 图16:使用命令"make btest"和命令“./btest -f bitXor” 所示。我们已成功编写了bitXor函数。
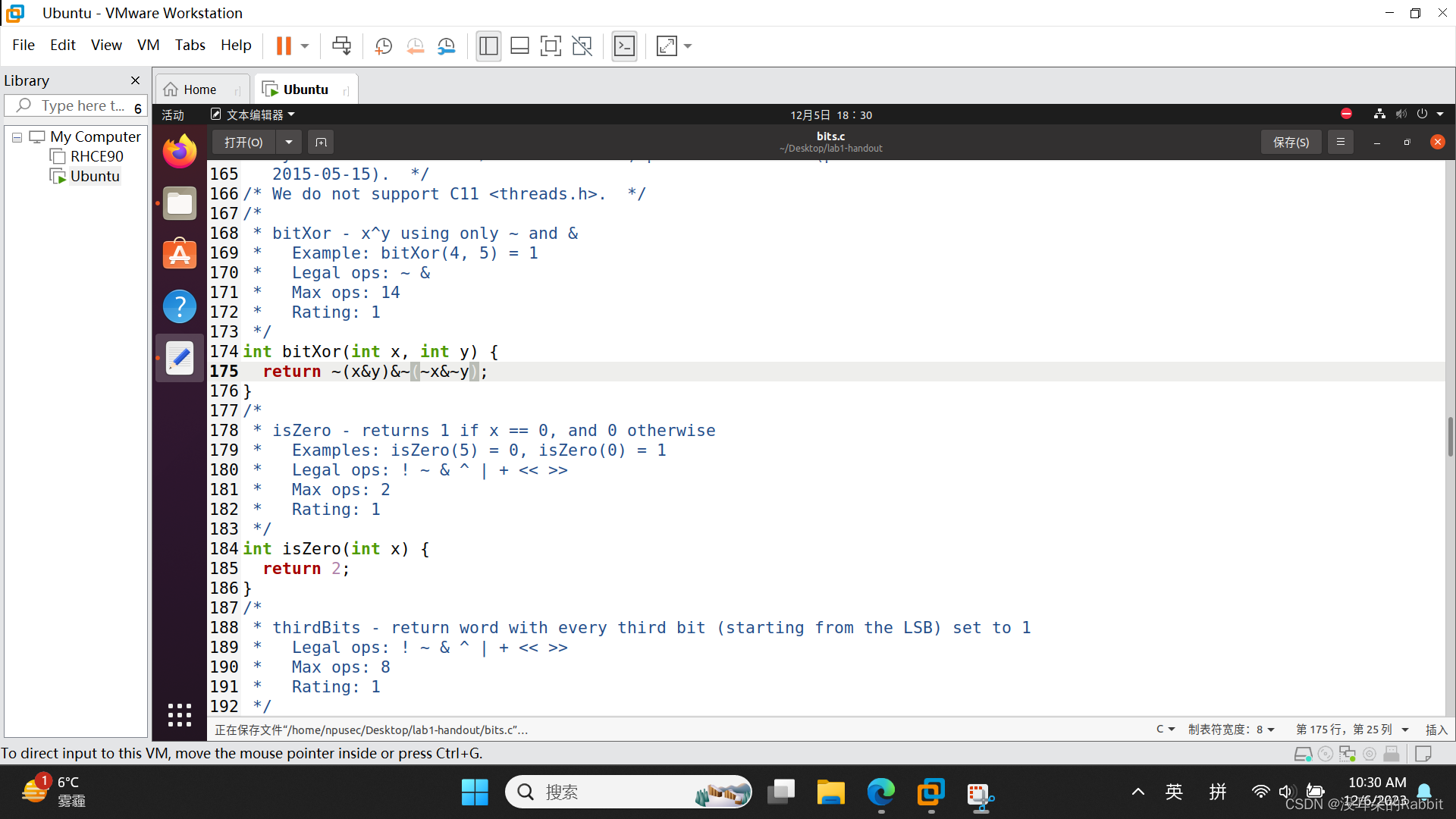
(图13:编写完成第1个函数bitXor)

(图14:在包含bits.c文件的文件夹中打开命令行)

(图15:使用命令"./dlc -e bits.c"和命令"make clean" 。使用命令"./dlc -e bits.c"查看运算符的数量是否满足要求以及是否满足其它的要求。如果除了对各个函数所使用到的运算符进行计数之后就没有其它的输出,那么表明满足运算符和其它的要求。接着使用"make clean"命令清除掉上一次遗留的旧的文件)
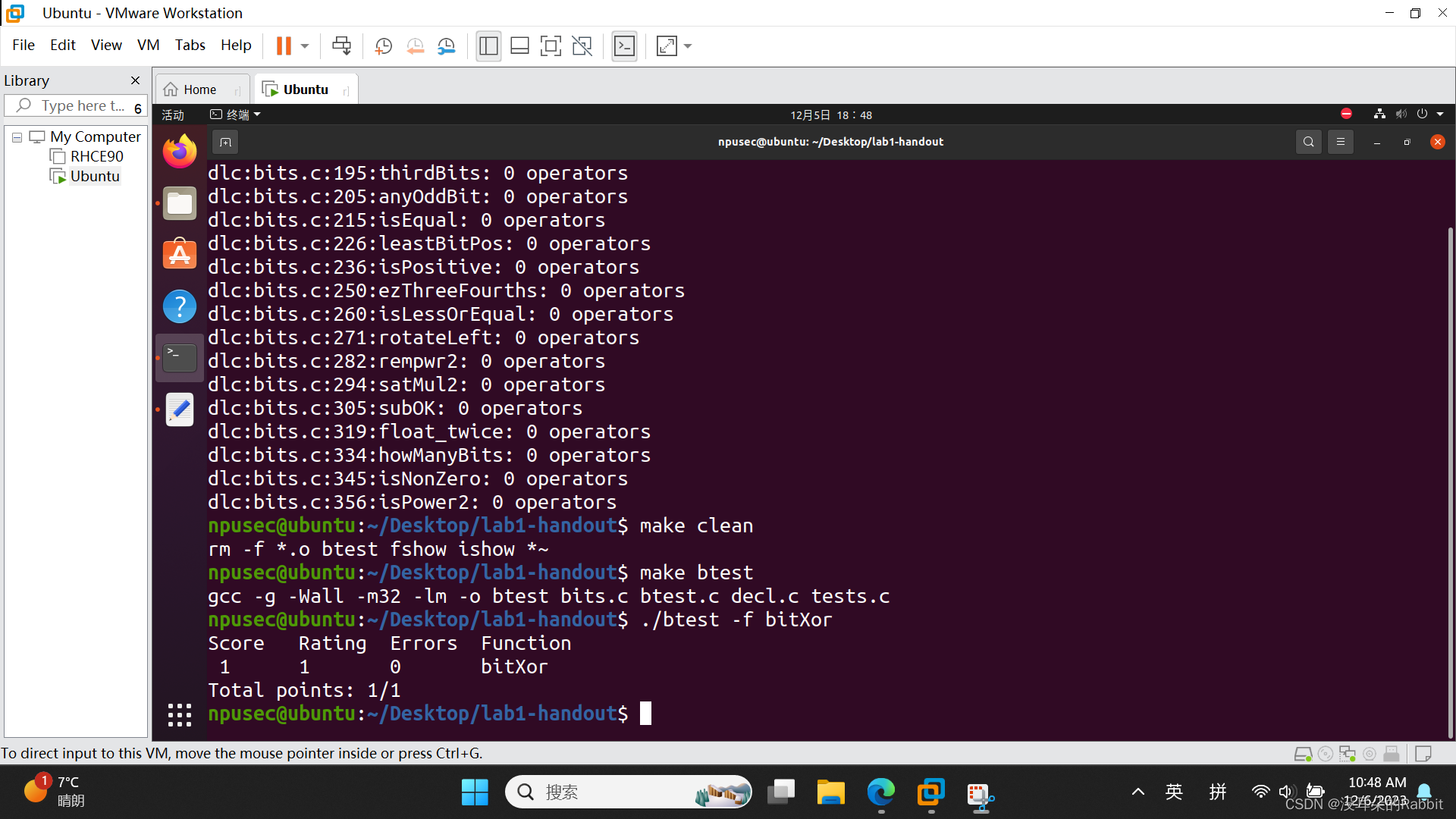
(图16:使用命令"make btest"和命令“./btest -f bitXor”)
接着第二个函数,isZero,当x为0时,返回1,当x不为0时,返回0,所以只需要简单的写"return !x"即可,如 图17:编写第2个函数isZero 和 图18:重复编写第1个函数时的操作 所示。

(图17:编写第2个函数isZero)
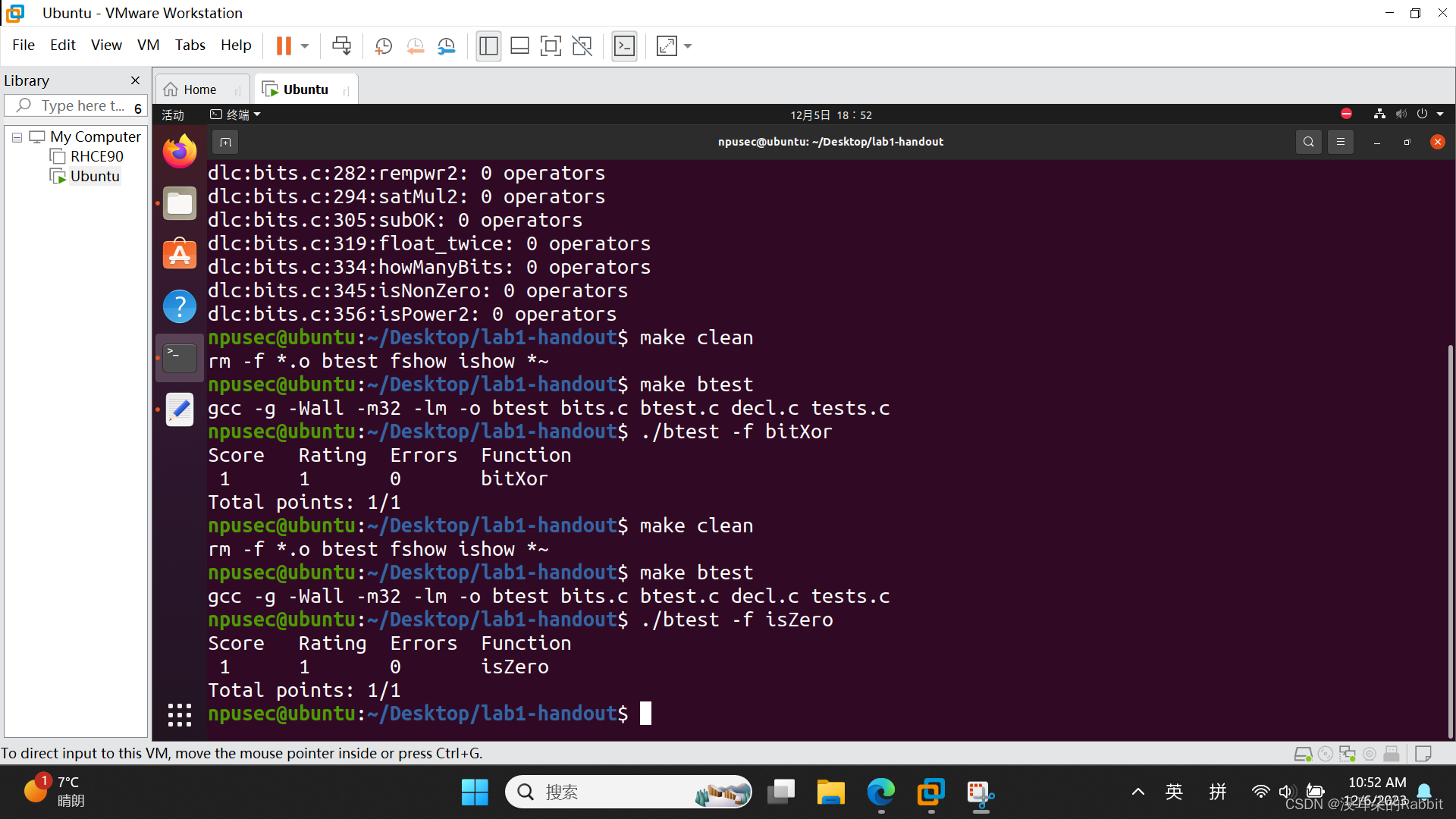
(图18:重复编写第1个函数时的操作。使用命令"./dlc -e bits.c"统计各个函数使用到的运算符的个数,使用命令"make clean"清除掉上一次遗留下来的旧的可执行文件,使用命令"make btest"生成新的btest可执行文件,使用命令"./btest -f isZero"检验所写函数isZero的正确性)
第三个函数,thirdBits,要我们自己产生一个int型的数,保证它从最低有效位开始,每第三个比特位被设置为1,即期望我们返回的数是:0100 1001 0010 0100 1001 0010 0100 1001B。但是根据要点二中的一句话:只能使用0x0到0xFF的int型常量,即我们不能直接返回它。那么应该怎么产生这个数呢?我们发现,可以先产生一个小于0xFF的int型常量,让它既满足从最低有效位开始,每第三个比特位被设置为1,又满足小于0xFF,而这个数就是0x49,它的二进制表示形式为0100 1001。接着让0x49左移9位,得到了1001 0010 0000 0000,左移9位的目的就是为了让其既能保证,除了低9位以外,从最低有效位开始,每第三个比特位被设置为1,又是0x49左移所能完成这个任务的极限。接着将0x49与0x49<<9拼凑在一起,得到了0000 0000 0000 0000 1001 0010 0100 1001,它结合了0x49和0x49<<9的优点,保证了最大程度上从最低有效位开始,每第三个比特位被设置为1。但是,最高的16个比特位还没有被处理,而这可以简单的通过((0x49<<9)+0x49)<<18来实现。最后将0x49、0x49<<9与((0x49<<9)+0x49)<<18拼凑起来,即为最终的答案。而为了节省运算符,我们使用int型变量t来保存((0x49<<9)+0x49),接着"return t+(t<<24)"即可。具体的五个步骤为:
-
期望的输出: 0100 1001 0010 0100 1001 0010 0100 1001
-
第一个步骤: 0000 0000 0000 0000 0000 0000 0100 1001 0x49
-
第二个步骤: 0000 0000 0000 0000 1001 0010 0000 0000 0x49<<9
-
第三个步骤: 0000 0000 0000 0000 1001 0010 0100 1001 (0x49<<9)+0x49
-
第四个步骤: 0100 1001 0010 0100 0000 0000 0000 0000 ((0x49<<9)+0x49)<<18
-
第五个步骤: 0100 1001 0010 0100 1001 0010 0100 1001 (((0x49<<9)+0x49)<<18)+(0x49<<9)+0x49
如 图19:编写第3个函数thirdBits 所示。


(图19:编写第3个函数thirdBits)
第4个函数anyOddBit,如果x中,只要有一个第奇数个比特位被设置为了1,那么就返回1,否则返回0,比如7是0111,其第0、1、2个比特位为1,满足第1个比特位被设置为1,返回1;比如5是0101,第0、2个比特位为1,不满足第奇数个比特位被设置为1,也就是第1个比特位没有被设置为1,所以返回0,注意这里特别容易混淆,作者因为搞混了这一点,废了好多功夫。我们的思路就是,先产生1010 1010 1010 1010 1010 1010 1010 1010,这个数是0xAAAAAAAA,它第1、3、5、7、9、11... ...31个比特位都被设置为了1,然后将0xAAAAAAAA与x做位与操作,这样子获取x的所有奇数比特位,如果x中存在一个奇数比特位被设置为1,那么位与的结果就不为0,此时连用两个逻辑非!,即可得到1,如果x中所有奇数比特位都是0,那么位与的结果就是0,此时连用两个逻辑非!,即可得到0。那么我们该如何得到0xAAAAAAAA呢?可以按照下面的五个步骤来得到0xAAAAAAAA。为了节省运算符,引入int a=0xAA,int b=0xAA<<8,int c=a+b,int d=(c<<16)+c,这时d即为0xAAAAAAAA。然后编写第四个函数anyOddBit,如 图20:编写第4个函数anyOddBit 所示。
-
期望的输出: 1010 1010 1010 1010 1010 1010 1010 1010 0xAAAAAAAA
-
第一个步骤: 0000 0000 0000 0000 0000 0000 1010 1010 0xAA
-
第二个步骤: 0000 0000 0000 0000 1010 1010 0000 0000 0xAA<<8
-
第三个步骤: 0000 0000 0000 0000 1010 1010 1010 1010 (0xAA<<8)+0xAA
-
第四个步骤: 1010 1010 1010 1010 0000 0000 0000 0000 ((0xAA<<8)+0xAA)<<16
-
第五个步骤: 1010 1010 1010 1010 1010 1010 1010 1010 (((0xAA<<8)+0xAA)<<16)+((0xAA<<8)+0xAA)


(图20:编写第4个函数anyOddBit)
第5个函数,isEqual,如果两个int型数相等,那么返回1,否则返回0,我们直接!(x^y)即可。如 图21:编写第5个函数isEqual 所示。
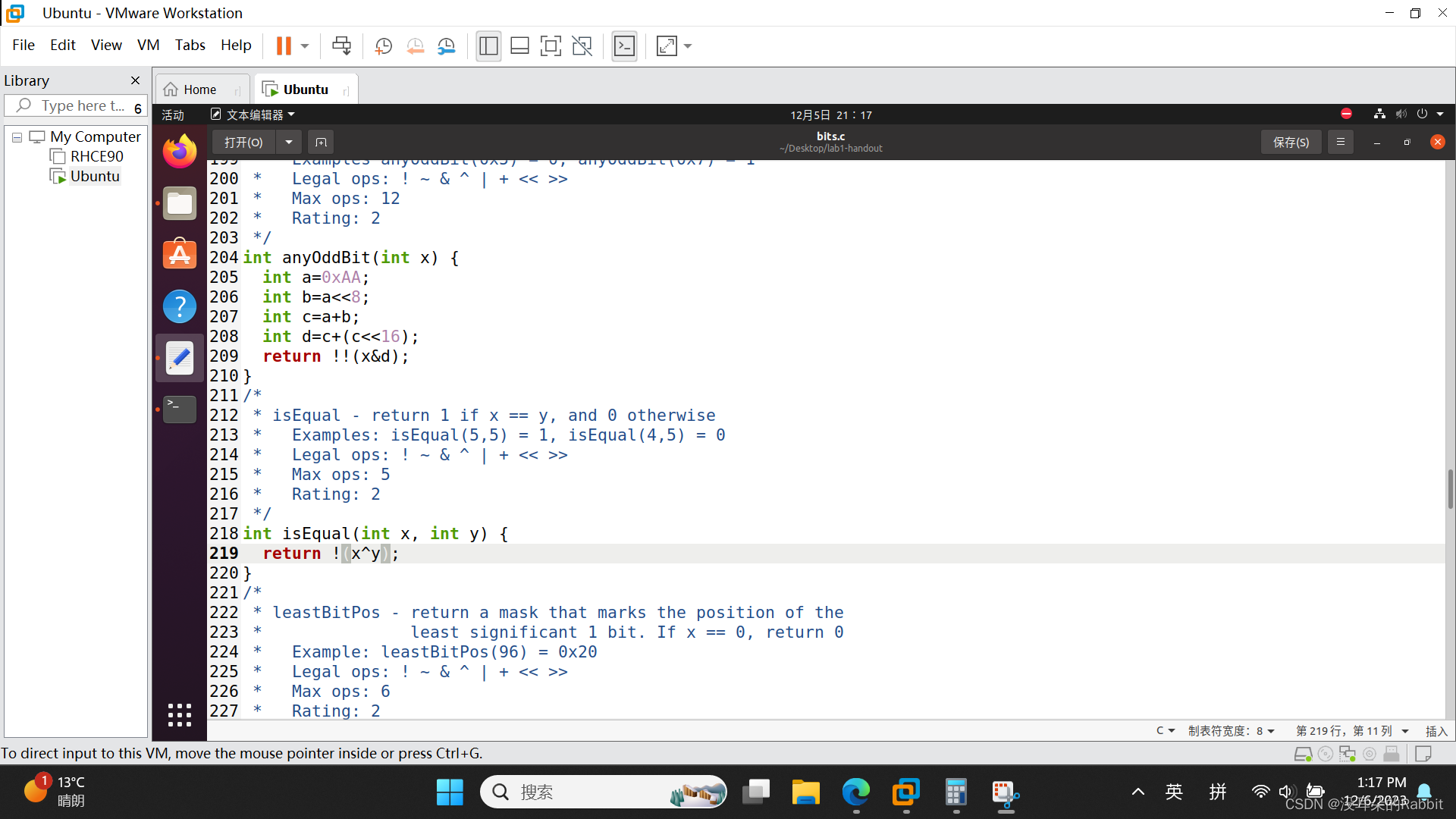

(图21:编写第5个函数isEqual)
第6个函数,leastBitPos,可以理解为,找到从左到右最后一个1的位置,然后其它位置都设为0。对于96来说,96可以写成0110 0000,最低位的1是从右往左第5个,所以返回0010 0000;对于104来说,104可以写成0110 1000,从左到右最后一个1的位置是第3个,所以返回0000 1000。那么我们该怎么做呢?发现可以将x各位取反然后加1,并将这个结果与x进行位与,这时返回的结果即为我们期望中的结果。比如对于96,也就是0110 0000来说,各位取反得到了1001 1111,再加1得到了1010 0000,然后将这个数与0110 0000进行位与操作,得到了0010 0000,正好是我们想要的结果,所以我们"return ((~x)+1)&x;"即可,如 图22:编写第6个函数leastBitPos 所示。

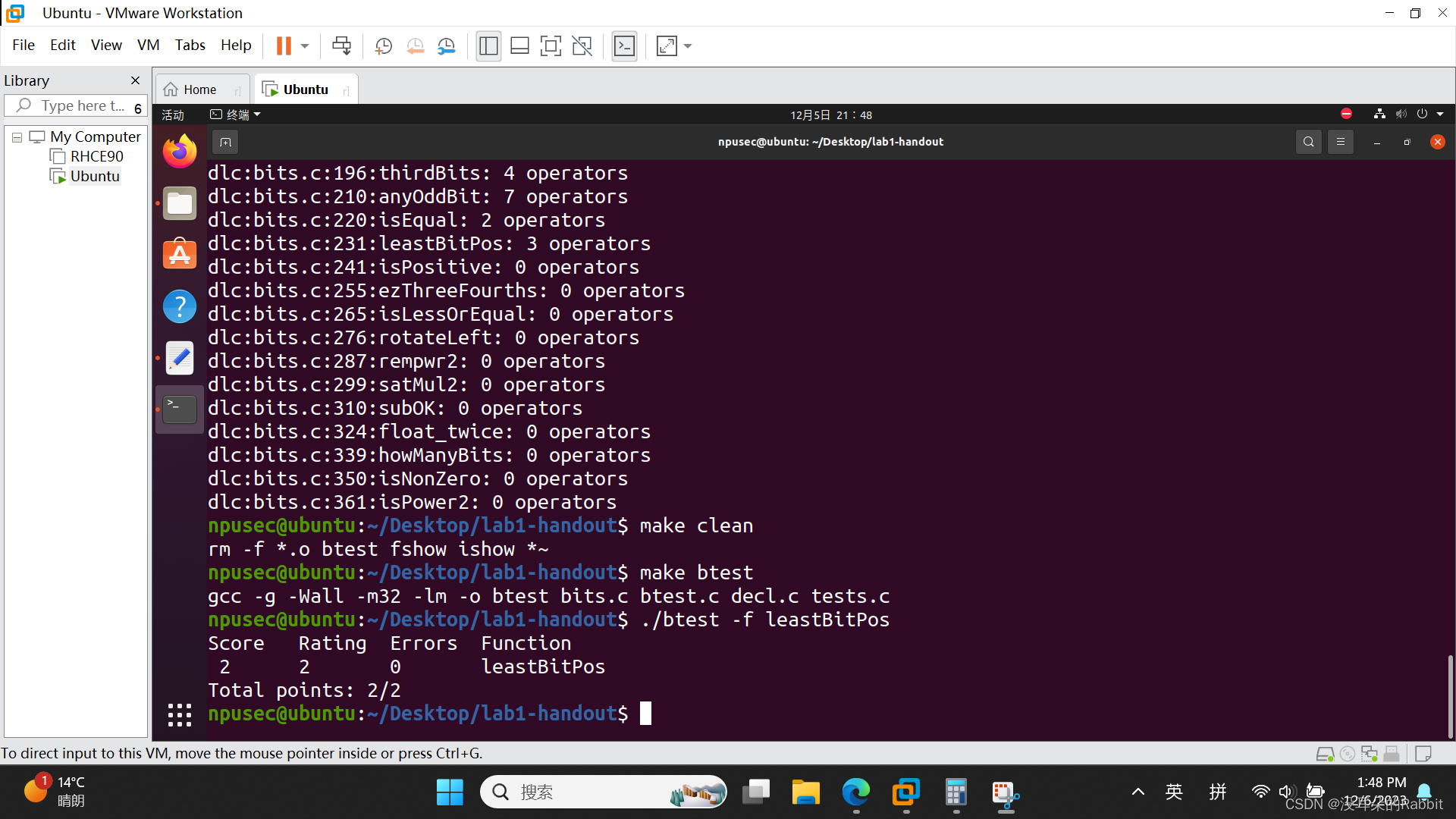
(图22:编写第6个函数leastBitPos)
接着第7个函数,isPositive, 如果x大于0的话返回1,如果x不大于0的话返回0。该怎么做呢?只需要判断符号位即可。该怎么获取符号位呢?可以将x右移31位,因为一方面针对int型变量的右移都是算术右移,另外一方面实验也规定了所有的右移都是算术右移,所以我们将x右移31位,这样所有的比特位都和符号位是一样的取值了。这时得到!(x>>31),如果x为正,则符号位为0,x>>31为0,逻辑非后为1;如果x为负,则符号位为1,x>>31为0xFFFFFFFF,逻辑非后为0。另外考虑到当x为0时,本想让其返回0,结果此时!(x>>31)的结果也是1,所以需要修正,修正的结果为!(x>>31)&!!x,进而可以写成!(!x|x>>31)。当x为0时,!x为1,!x|x>>31直接为1,!(!x|x>>31)为0;当x为负数时,!x为0,x>>31为0xFFFFFFFF,!(!x|x>>31)为0;当x为正数时,!x为0,x>>31也为0,进而!(!x|x>>31)为1,按照这个思路,我们写出了"return !(!x|x>>31)",如 图23:编写第7个函数isPositive 所示。


(图23:编写第7个函数isPositive)
第8个函数,ezThreeFourths,开始慢慢变复杂了,我们需要完美复现C语言表达式x*3/4,那么该怎么做呢?首先计算x*3,x*3可以用位运算表示为(x<<1)+x,接着计算x/4,这里并不能简单的((x<<1)+x)>>2。为什么呢?因为如果简单的这样做以后,会存在当x为负数时舍入的问题,比如当x=-1、-2、-3、-5、-6、-7... ...时,((x<<1)+x)>>2会比x*3/4小1,而当x=-4、-8、-12时,((x<<1)+x)>>2才会与x*3/4相等。所以为了解决这个问题,进行修正,设a=(x<<1)+x,修正为(a+(a>>31)&0x3)>>2,这样子就可以啦!如 图24:编写第8个函数ezThreeFourths 所示。
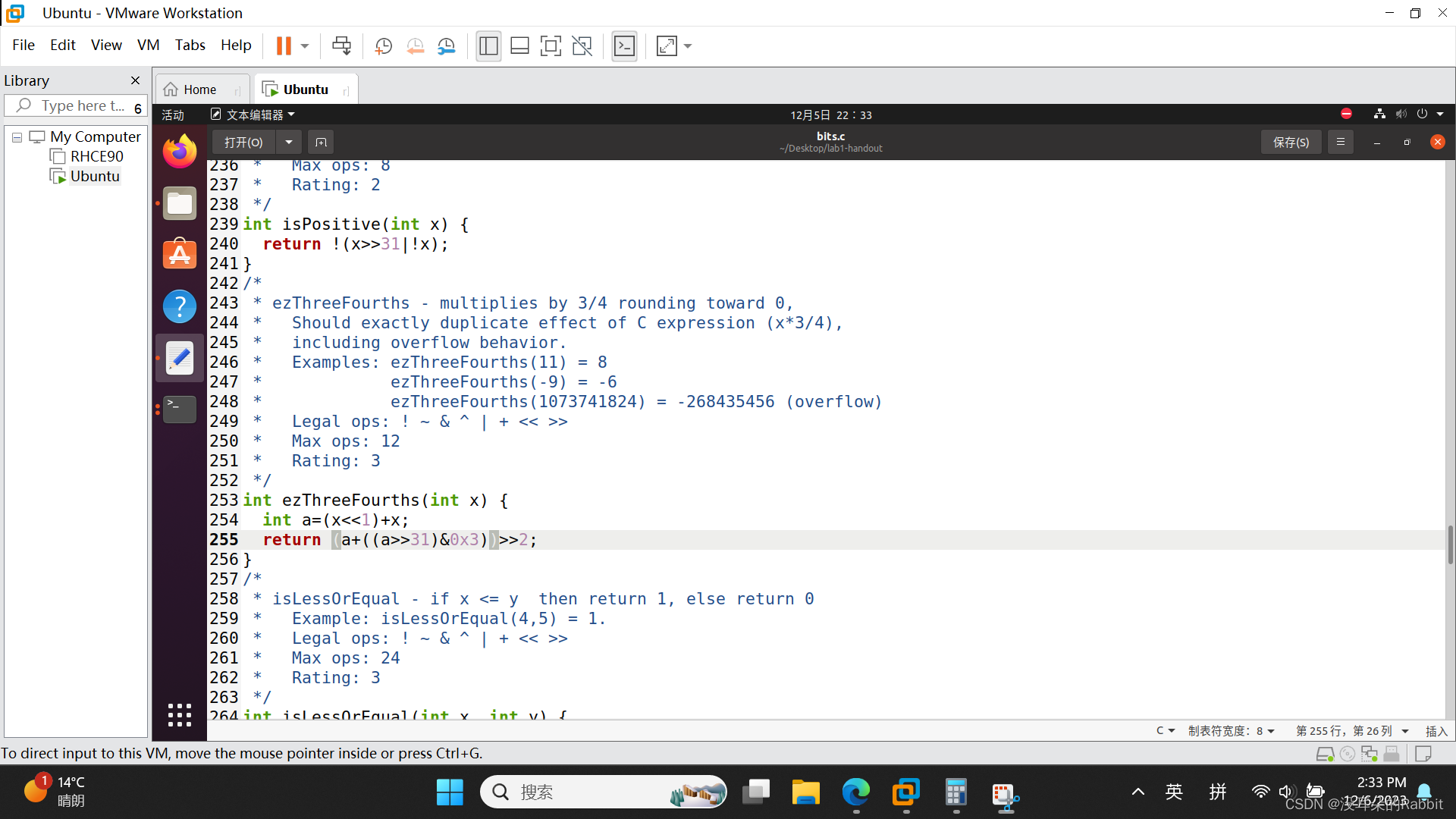

(图24:编写第8个函数ezThreeFourths)
第9个函数,isLessOrEqual。首先从大方向上来看,存在一个或的情况,也就是说,当x等于y时也返回1,所以大框架为:
( ) | ( !(x^y) )
这样子解决了或的问题,下一步就应该要解决isLess的问题。怎么解决这个问题呢?第一反应是通过计算x-y=x+~y+1,根据结果的符号位来判断是否小于。但问题在于,虽然一般情况下这种方法是对的,但如果是一个很小的负数减去一个很大的正数,或者一个很大的正数减去一个很小的负数,这时int类型就无法表示相减的结果,甚至无法表示1-0x8000 0000的结果。所以就需要根据int类型能不能放得下相减的结果,来进行分类讨论。那么如何判断int类型能不能放得下相减的结果呢?我们发现,只有当x与y异号时才存在溢出的问题,所以我们可以将x与y是否同号作为分类依据,这样子大框架进一步细分为:
(( (x^~y)&( ) | ( ) ) >>31)&1 | ( !(x^y) )
当x与y同号时,x与~y异号,x^~y的符号位为1,此时x-y的符号位为即为我们想返回的结果,所以直接返回x-y即可,这时大框架即为:
(( (x^~y)&(x+~y+1) | ( ) ) >>31)&1 | ( !(x^y) )
而当x与y异号时,x与~y同号,x^~y的符号位为0,此时选择x&~y,如果x符号位为0,那么x一定大于y,最终应该返回0,而x&~y恰好就是0;如果x符号位为1,那么x一定小于y,最终应该返回1,而x&~y恰好就是1。利用这个性质,最终的大框架即可完成:
(( (x^~y)&(x+~y+1) | ( x&~y ) ) >>31)&1 | ( !(x^y) )
而如果只选择直接看x的符号位是否为1,而不是选择x&~y的话,有可能出现x与y同号并且x-y符号位为0并且x符号位为1,这时(x^~y)&(x+~y+1)符号位为0,x符号位为1,0|1为1,返回1,但我们想要其返回0,这就出现了冲突。为了避免这个冲突,就需要保证当x与y同号,x^~y的符号位为1时,我们选择的表达式一定为0,所以这才选择了x&~y。有些同学会问,那我们最开始的时候,为什么不写成( !!(x^y)&() ) | ( !(x^y) ),是不是也是这个道理呢?对。因为当!(x^y)为1,即x==y时,!!(x^y)&()中的()一定为0,所以我们才选择省略了!!(x^y)。最终,如 图25:编写第9个函数isLessOrEqual 所示。


(图25:编写第9个函数isLessOrEqual)
第10个函数,rotateLeft,将x旋转左移n位。比如0x87654321左移4位得到了0x76543218,该怎么得到0x76543218呢?我们发现,其由两部分组成,分别是0x76543210与0x8。0x76543210可直接由x<<4得到,0x8可有x>>28然后与0xF做位与得到。最终4可被n代替,28可被32+~n+1代替,那么如何得到0xF呢?最省运算符的方法是,~0+(1<<n)。所以按照这个思路,我们可写出表达式为"(x<<n)|((x>>(32+~n+1))&(~0+(1<<n)))",最终如 图26:编写第10个函数rotateLeft 所示。


(图26:编写第10个函数rotateLeft)
/* * bitXor - x^y using only ~ and & * Example: bitXor(4, 5) = 1* Legal ops: ~ &* Max ops: 14* Rating: 1*/
int bitXor(int x, int y) {return ~(x&y)&~(~x&~y);
}
/** isZero - returns 1 if x == 0, and 0 otherwise * Examples: isZero(5) = 0, isZero(0) = 1* Legal ops: ! ~ & ^ | + << >>* Max ops: 2* Rating: 1*/
int isZero(int x) {return !x;
}
/* * thirdBits - return word with every third bit (starting from the LSB) set to 1* Legal ops: ! ~ & ^ | + << >>* Max ops: 8* Rating: 1*/
int thirdBits(void) {int t=0x49+(0x49<<9);return t+(t<<18);
}
/* * anyOddBit - return 1 if any odd-numbered bit in word set to 1* Examples anyOddBit(0x5) = 0, anyOddBit(0x7) = 1* Legal ops: ! ~ & ^ | + << >>* Max ops: 12* Rating: 2*/
int anyOddBit(int x) {int a=0xAA;int b=a<<8;int c=a+b;int d=c+(c<<16);return !!(x&d);
}
/* * isEqual - return 1 if x == y, and 0 otherwise * Examples: isEqual(5,5) = 1, isEqual(4,5) = 0* Legal ops: ! ~ & ^ | + << >>* Max ops: 5* Rating: 2*/
int isEqual(int x, int y) {return !(x^y);
}
/* * leastBitPos - return a mask that marks the position of the* least significant 1 bit. If x == 0, return 0* Example: leastBitPos(96) = 0x20* Legal ops: ! ~ & ^ | + << >>* Max ops: 6* Rating: 2 */
int leastBitPos(int x) {return ((~x)+1)&x;
}
/* * isPositive - return 1 if x > 0, return 0 otherwise * Example: isPositive(-1) = 0.* Legal ops: ! ~ & ^ | + << >>* Max ops: 8* Rating: 2*/
int isPositive(int x) {return !(x>>31|!x);
}
/** ezThreeFourths - multiplies by 3/4 rounding toward 0,* Should exactly duplicate effect of C expression (x*3/4),* including overflow behavior.* Examples: ezThreeFourths(11) = 8* ezThreeFourths(-9) = -6* ezThreeFourths(1073741824) = -268435456 (overflow)* Legal ops: ! ~ & ^ | + << >>* Max ops: 12* Rating: 3*/
int ezThreeFourths(int x) {int a=(x<<1)+x;return (a+((a>>31)&0x3))>>2;
}
/* * isLessOrEqual - if x <= y then return 1, else return 0 * Example: isLessOrEqual(4,5) = 1.* Legal ops: ! ~ & ^ | + << >>* Max ops: 24* Rating: 3*/
int isLessOrEqual(int x, int y) {
return ((((((x+~y+1)&(x^~y))|(x&~y))>>0x1f))&1)|!(x^y);
}
/* * rotateLeft - Rotate x to the left by n* Can assume that 0 <= n <= 31* Examples: rotateLeft(0x87654321,4) = 0x76543218* Legal ops: ~ & ^ | + << >> !* Max ops: 25* Rating: 3 */
int rotateLeft(int x, int n) {return (x<<n)|((x>>(32+~n+1))&(~0+(1<<n)));
}相关文章:

西工大计算机学院计算机系统基础实验一(函数编写1~10)
还是那句话,千万不要慌,千万不要着急,耐下性子慢慢来,一步一个脚印,把基础打的牢牢的,一样不比那些人差。回到实验本身,自从按照西工大计算机学院计算机系统基础实验一(…...

VMware 虚拟机 电脑重启后 NAT 模式连不上网络问题修复
问题描述: 昨天 VMware 安装centos7虚拟机,网络模式配置的是NAT模式,配置好后,当时能连上外网,今天电脑重启后,发现连不上外网了 检查下各个配置,都没变动,突然就连不上了 网上查了…...
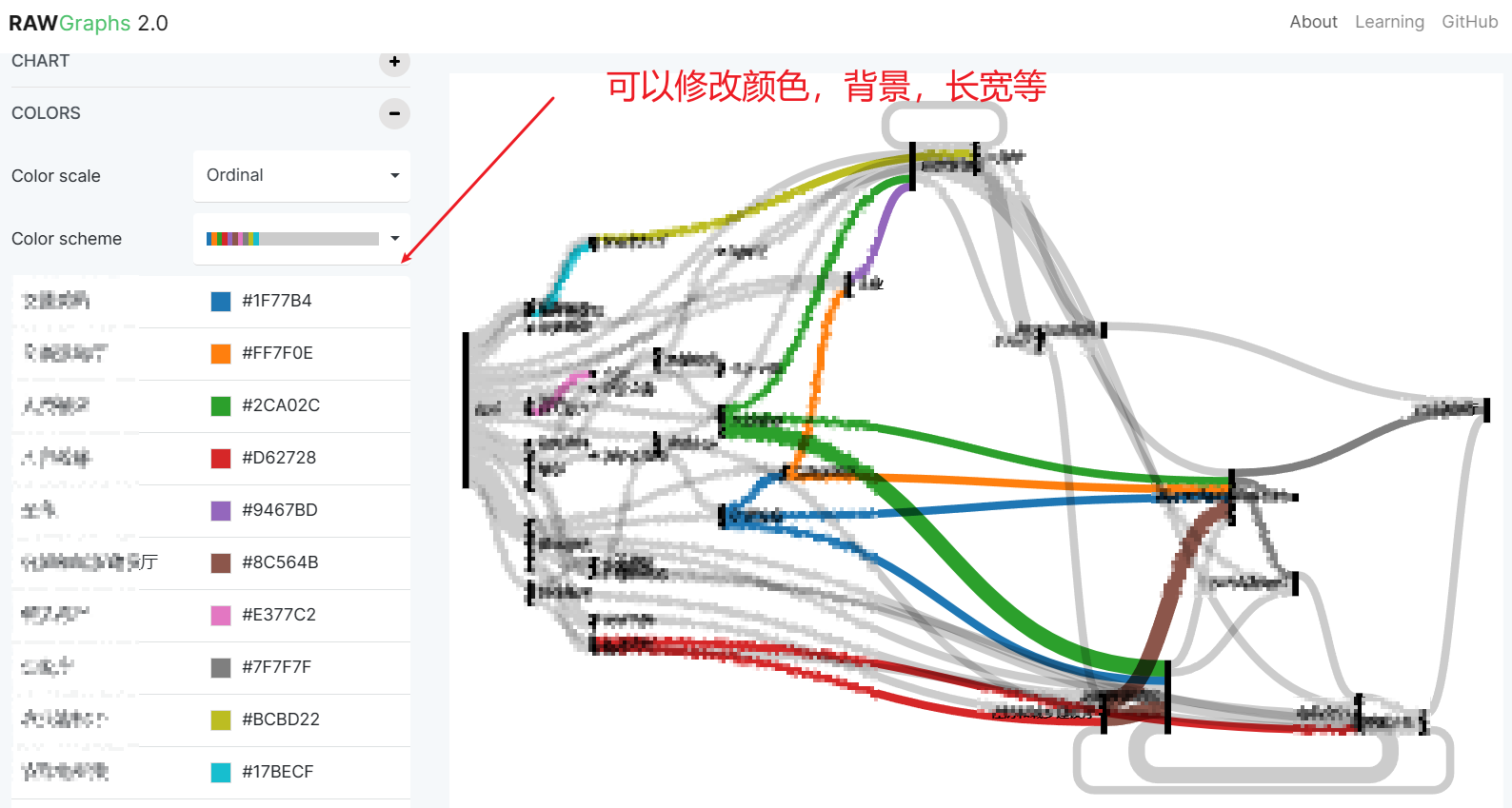
【桑基图】绘制桑基图
绘制桑基图 一、绘制桑基图(1)方法一:去在线网站直接绘制(2)方法二:写html之后在vscode上运行 二、遇到的问题(1)当导入一些excel的时候,无法绘制出桑基图 一、绘制桑基图…...
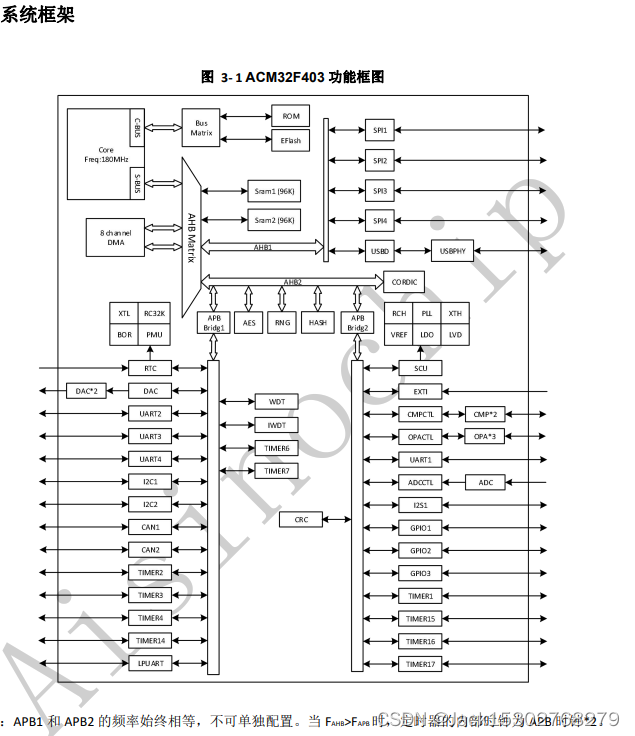
ACM32F403/F433 12 位多通道,支持 MPU 存储保护功能,应用于工业控制,智能家居等产品中
ACM32F403/F433 芯片的内核基于 ARMv8-M 架构,支持 Cortex-M33 和 Cortex-M4F 指令集。芯片内核 支持一整套DSP指令用于数字信号处理,支持单精度FPU处理浮点数据,同时还支持Memory Protection Unit (MPU)用于提升应用的…...
7. 从零用Rust编写正反向代理, HTTP及TCP内网穿透原理及运行篇
wmproxy wmproxy是由Rust编写,已实现http/https代理,socks5代理, 反向代理,静态文件服务器,内网穿透,配置热更新等, 后续将实现websocket代理等,同时会将实现过程分享出来ÿ…...
UE4.27-UE5.1设置打包Android环境
打包Android配置文件 1. 配置打包Android的SDK需求文件位于下面文件中: 2. 指定了对应的SDK环境变量名字以及NDK需求等: UE4.27-UE5.1--脚本自动配置 安装前提 1. 务必关闭虚幻编辑器和Epic Games Launcher,以确保NDK组件的安装或引擎环境…...

MySQL授权密码
mysql> crate databases school charcter set utf8; Query OK, 1 row affected, 1 warning (0.00 sec) 2.在school数据库中创建Student和Score表 mysql> use school Database changed mysql> create table student-> -> (id int(10) primary key auto_incremen…...
0X05
打开题目 点击完登录和注册都没有什么反应,所以先扫一下看看 在出现admin.php后就截止了,访问看看,进入后台。。 尝试一下弱口令 admin/12345 或者是demo/demo 设计中-自定义->右上角导出主题 找到一个导出的点,下载了一个1.zip压缩包…...

Doris优化总结
1 查看QueryProfile 利用查询执行的统计结果,可以更好的帮助我们了解Doris的执行情况,并有针对性的进行相应Debug与调优工作。 FE将查询计划拆分成为Fragment下发到BE进行任务执行。BE在执行Fragment时记录了运行状态时的统计值,并将Fragment执行的统计信息输出到日志之中。…...
案例059:基于微信小程序的在线投稿系统
文末获取源码 开发语言:Java 框架:SSM JDK版本:JDK1.8 数据库:mysql 5.7 开发软件:eclipse/myeclipse/idea Maven包:Maven3.5.4 小程序框架:uniapp 小程序开发软件:HBuilder X 小程序…...

利用STM32内置Bootloader实现USB DFU固件升级
本文将介绍如何利用STM32内置的Bootloader来实现USB DFU(Device Firmware Upgrade)固件升级功能。首先,我们会介绍USB DFU的原理和工作流程。然后,我们将详细讲解如何配置STM32芯片以支持USB DFU,并提供相应的代码示例…...

Centos7如何安装MySQL
目录 一、卸载mysql 二、安装mysql 注:本文主要是看了这位大佬安装MySQL,才想着写一篇记录一下。 一、卸载mysql 安装mysql之前一定要将之前安装的mysql相关文件删除干净,防止出现错误。 (1)关闭mysql 开启了mysql就…...

VR远程带看,助力线下门店线上化转型“自救”
VR远程带看,因自身高效的沉浸式在线沟通功能,逐渐走进了大众的视野。身临其境的线上漫游体验以及实时同屏互联的新型交互模式,提升了商家同用户之间的沟通效率,进一步实现了远程线上一对一、一对多的同屏带看,用户足不…...
算法通关村第十七关-白银挑战贪心算法高频题目
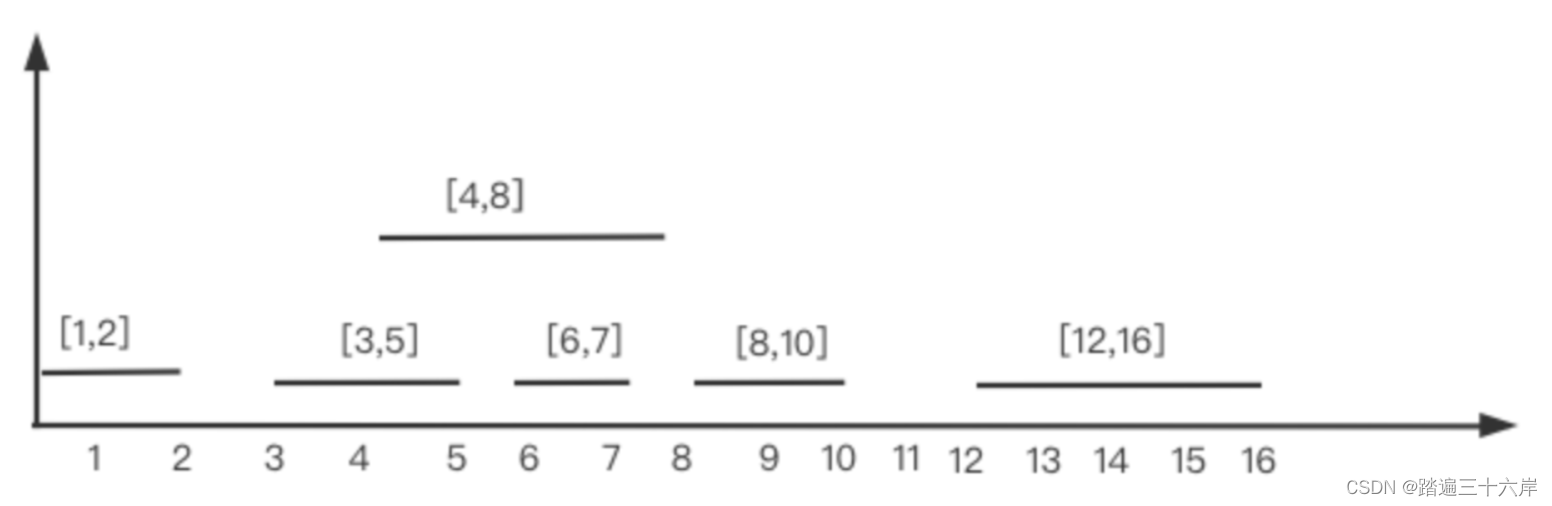
大家好我是苏麟 , 今天说说贪心算法的高频题目 . 大纲 区间问题判断区间是否重叠合并区间插入区间 区间问题 判断区间是否重叠 描述 : 给定一个会议时间安排的数组 intervals ,每个会议时间都会包括开始和结束的时间intervalsl[i] [start, end] ,请你…...
【数据结构】动态规划(Dynamic Programming)
一.动态规划(DP)的定义: 求解决策过程(decision process)最优化的数学方法。 将多阶段决策过程转化为一系列单阶段问题,利用各阶段之间的关系,逐个求解。 二.动态规划的基本思想: …...
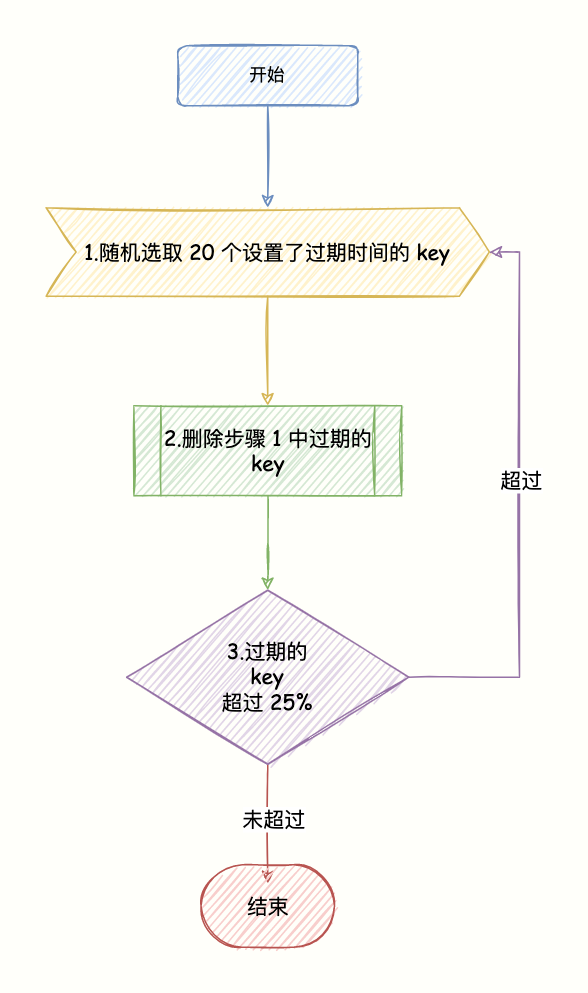
Redis key过期删除机制实现分析
文章目录 前言Redis key过期淘汰机制惰性删除机制定时扫描删除机制 前言 当我们创建Redis key时,可以通过expire命令指定key的过期时间(TTL),当超过指定的TTL时间后,key将会失效。 那么当key失效后,Redis会立刻将其删除么&#…...

ElasticSearch 谈谈分词与倒排索引的原理
ElasticSearch是一个基于Lucene的搜索服务器。Lucene是Java的一个全文检索工具包,而ElasticSearch则是一个分布式搜索和分析引擎。下面,我们将详细讨论ElasticSearch中的分词和倒排索引的原理。 分词: 在ElasticSearch中,分词是…...

【Java】Java8重要特性——Lambda函数式编程以及Stream流对集合数据的操作
【Java】Java8重要特性——Lambda函数式编程以及Stream流对集合数据的操作 前言Lambda函数式编程Stream流对集合数据操作(一)创建Stream流(二)中间操作之filter(三)中间操作之map(四)…...

大话数据结构-查找-散列表查找(哈希表)
注:本文同步发布于稀土掘金。 8 散列表查找(哈希表) 8.1 定义 散列技术是在记录的存储位置和它的关键字之间建立一个确定的对应关系f,使得每个关键字key对应一个存储位置f(key)。查找时,根据这个确定的对应关系找到给…...

持续集成交付CICD:Sonarqube自动更新项目质量配置
目录 一、实验 1.Sonarqube手动自定义质量规则并指定项目 2.Sonarqube自动更新项目质量配置 一、实验 1.Sonarqube手动自定义质量规则并指定项目 (1)自定义质量规则 ①新配置 ②更多激活规则③根据需求激活相应规则④已新增配置 ⑤ 查看 &#x…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...
