【数据结构】动态规划(Dynamic Programming)
一.动态规划(DP)的定义:
求解决策过程(decision process)最优化的数学方法。
将多阶段决策过程转化为一系列单阶段问题,利用各阶段之间的关系,逐个求解。
二.动态规划的基本思想:
与分治法类似,将待求解问题分解成若干个子问题。
但是经分解得到的子问题往往不是相互独立的。
如果使用分治法求解问题,有些子问题被重复计算了多次。
而“如何减少子问题的重复计算”是动态规划算法的关键思想。
问题:如何减少子问题的重复计算呢?
解决方案:保存已解决的子问题的答案,在需要的时候找出已经求得的答案。
三.动态规划的基本步骤
1.找出最优解的性质,并刻划其结构特征。即:寻找最优解的子问题结构。
2.递归地定义最优解。即:根据子问题的结构建立问题的递归解式,求解最优值。
3.以自底向上的方式计算出最优值。
4.根据计算最优值时得到的信息,构造最优解。
四.例题分析——多个矩阵连乘模块设计
问题描述:
实现多个矩阵连乘功能
关键问题计算:
给定n个矩阵{},其中
与
是可乘的,考察这n个矩阵的连乘积
由于矩阵乘法满足结合律,所以计算矩阵的连乘可以有许多不同的计算次序。这种计算次序可以用加括号的方式来确定。
若一个矩阵连乘积的计算次序完全确定,也就是说该矩阵已完全加括号,则可以依此次序反复调用3个矩阵相乘的标准算法计算出矩阵连乘积。
完全加括号的矩阵连乘积:
设有四个矩阵 A,B,C,D 维数分别为:
50*10;10*40;40*30;30*5
则总共有五种完全加括号的方式:
1)
(A((BC)D))
2)
(A(B(CD)))
3)
((AB)(CD))
4)
(((AB)C)D)
5)
((A(BC))D)
对于两个矩阵A(p*q)*B(q*r)(标准乘法计算):
void matrixMultiply(int *a,int *b,int *c,int ra,int ca,int rb,int cb){if(ca!=rb){cout<<"矩阵不可乘!"<<endl;}else{int i,j,k,n,sum=0;for(i=0;i<ra;i++){for(j=0;j<cb;j++){for(k=0;k<ca;k++){sum+=a[i*ca+k]*b[k*cb+j];}c[i*ra+j]=sum;sum=0;}}}
}需要进行p*q*r次乘法计算!
矩阵连乘问题转化为:
确定矩阵连乘的计算次序,使得按照该次序计算矩阵连乘需要的数乘次数最少。
1.穷举法求解思路:
列举出所有可能的计算次序,并计算出每一种次序相应需要的数乘次数,从中找出一种数乘次数最少的计算次序。
算法复杂度分析:
对于n个矩阵的连乘积,设其不同的计算次序为P(n)
由于每种加括号方式都可以分解为两个子矩阵的加括号的问题

2.动态规划求解:
最优解结构分析:
将矩阵连乘积简记为:A[i:j],这里i<=j。
设这个计算次序在和
之间将矩阵断开,i<=k<j,则其相应的完全加括号的方式为:
()(
)
总计算量=A[i:k]的计算量加上A[k+1:j]的计算量,再加上A[i:k]和A[k+1:j]相乘的计算量。
特征:计算A[i:j]的最优次序所包含的计算矩阵子链A[i:k]和A[k+1:j]的次序也是最优的。
最优子结构性质:最优解包含其子问题的最优解。
建立递归关系:(m[i,j]表示最小连乘次数)
当i=j时,A[i:j]=,m[i,j]=0
当i<j时,m[i,j]={m[i,k]+m[k+1,j]+
}
则有:

(k的位置只有j-i种可能)
注:由于矩阵乘法中的列数和
的行数相等,则可以只用列数来化简表达式,这里的
均表示第i-1,k,j个矩阵的列数。n个矩阵的信息,只需要一个长度为n+1的数组来表示即可。
对于m[i][j]数组,只需要填入上三角中的元素即可(因为i<=j)。
五.代码实现
#include <iostream>
using namespace std;
int BestValue(int row[],int col[], int n);
int main(int argc, const char * argv[]) {int row[]={3,4,6};int col[]={4,6,11};cout<<BestValue(row, col, 3);return 0;
}
int BestValue(int row[],int col[], int n){if(n<=0){cout<<"error";return 0;}int m[40][40];int i,j,k,r,sum;for(i=0;i<n-1;i++){if(col[i]!=row[i+1]){cout<<"error"<<endl;return 0;}}for(i=0;i<n;i++){m[i][i]=0;}for(r=1;r<n;r++){for(j=r;j<n;j++){i=j-r;sum=m[i][i]+m[i+1][j]+row[i]*col[i]*col[j];for(k=i;k<j;k++){if(sum>m[i][k]+m[k+1][j]+row[i]*col[k]*col[j]){sum=m[i][k]+m[k+1][j]+row[i]*col[k]*col[j];}}m[i][j]=sum;}}return m[0][n-1];
}
相关文章:
【数据结构】动态规划(Dynamic Programming)
一.动态规划(DP)的定义: 求解决策过程(decision process)最优化的数学方法。 将多阶段决策过程转化为一系列单阶段问题,利用各阶段之间的关系,逐个求解。 二.动态规划的基本思想: …...
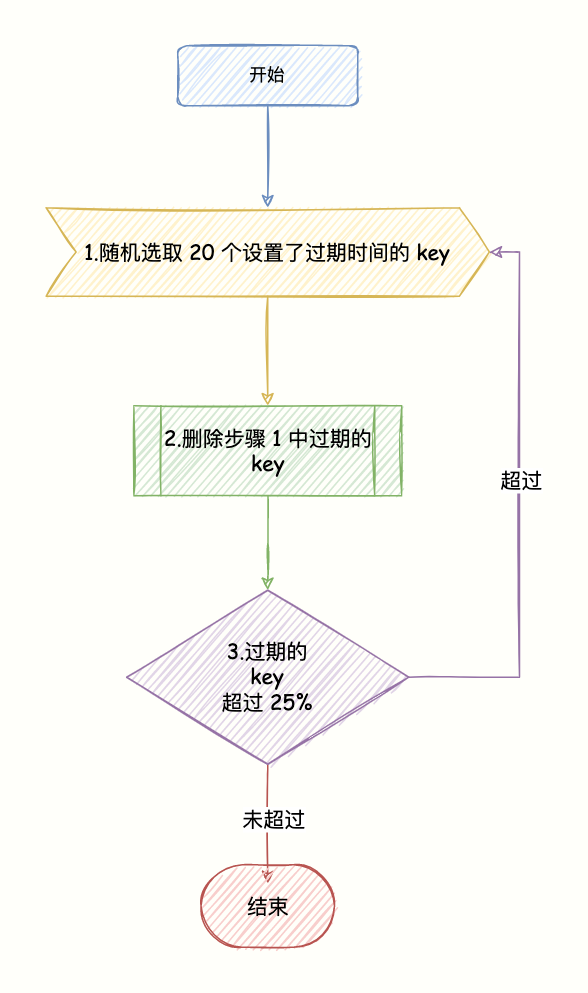
Redis key过期删除机制实现分析
文章目录 前言Redis key过期淘汰机制惰性删除机制定时扫描删除机制 前言 当我们创建Redis key时,可以通过expire命令指定key的过期时间(TTL),当超过指定的TTL时间后,key将会失效。 那么当key失效后,Redis会立刻将其删除么&#…...

ElasticSearch 谈谈分词与倒排索引的原理
ElasticSearch是一个基于Lucene的搜索服务器。Lucene是Java的一个全文检索工具包,而ElasticSearch则是一个分布式搜索和分析引擎。下面,我们将详细讨论ElasticSearch中的分词和倒排索引的原理。 分词: 在ElasticSearch中,分词是…...

【Java】Java8重要特性——Lambda函数式编程以及Stream流对集合数据的操作
【Java】Java8重要特性——Lambda函数式编程以及Stream流对集合数据的操作 前言Lambda函数式编程Stream流对集合数据操作(一)创建Stream流(二)中间操作之filter(三)中间操作之map(四)…...

大话数据结构-查找-散列表查找(哈希表)
注:本文同步发布于稀土掘金。 8 散列表查找(哈希表) 8.1 定义 散列技术是在记录的存储位置和它的关键字之间建立一个确定的对应关系f,使得每个关键字key对应一个存储位置f(key)。查找时,根据这个确定的对应关系找到给…...

持续集成交付CICD:Sonarqube自动更新项目质量配置
目录 一、实验 1.Sonarqube手动自定义质量规则并指定项目 2.Sonarqube自动更新项目质量配置 一、实验 1.Sonarqube手动自定义质量规则并指定项目 (1)自定义质量规则 ①新配置 ②更多激活规则③根据需求激活相应规则④已新增配置 ⑤ 查看 &#x…...

Linux设置Docker自动创建Nginx容器脚本
文章目录 前言一、本地新建脚本二、复制本地脚本到服务器三、执行服务器脚本总结如有启发,可点赞收藏哟~ 前言 一、本地新建脚本 在本地新建nginx-generator.sh脚本文件,并保存以下内容 主要动态定义两个变量(容器名称/服务器本地文件名、端…...
技术博客:Vue中各种混淆用法汇总
技术博客:Vue中各种混淆用法汇总 摘要 本文主要介绍了在Vue中使用的一些常见混淆用法,包括new Vue()、export default {}、createApp()、Vue.component、Vue3注册全局组件、Vue.use()等,以及如何使用混淆器对代码进行加固,保护应…...

【python】Python生成GIF动图,多张图片转动态图,pillow
pip install pillow 示例代码: from PIL import Image, ImageSequence# 图片文件名列表 image_files [car.png, detected_map.png, base64_image_out.png]# 打开图片 images [Image.open(filename) for filename in image_files]# 设置输出 GIF 文件名 output_g…...

python/matlab图像去雾/去雨综述
图像去雾和去雨是计算机视觉领域的两个重要任务,旨在提高图像质量和可视化效果。本文将综述图像去雾和去雨的算法、理论以及相关项目代码示例。 一、图像去雾算法 基于暗通道先验的方法: 这是广泛应用于图像去雾的经典算法之一。该方法基于一个观察&…...
Docker+jenkins+gitlab实现持续集成
1.安装环境 服务器ip虚拟机版本192.168.5.132centos7.6192.168.5.152centos7.6 2. 安装docker 安装必要的一些系统工具 yum install -y yum-utils device-mapper-persistent-data lvm2添加软件源信息,要确保centos7能上外网 yum-config-manager --add-repo http:…...

Web前端JS如何获取 Video/Audio 视音频声道(左右声道|多声道)、视音频轨道、音频流数据
写在前面: 根据Web项目开发需求,需要在H5页面中,通过点击视频列表页中的任意视频进入视频详情页,然后根据视频的链接地址,主要是 .mp4 文件格式,在进行播放时实时的显示该视频的音频轨道情况,并…...
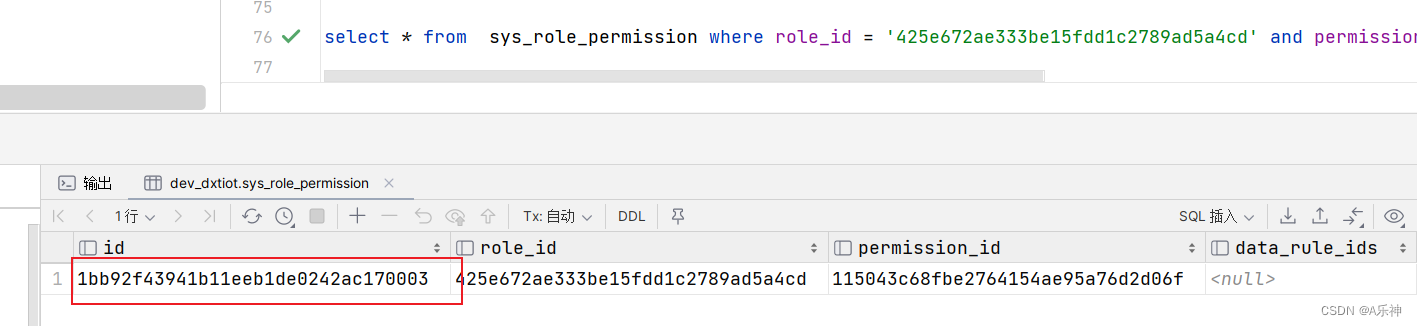
MySQL生成UUID并去除-
uuid()函数 uuid() 函数可以使mysql生成uuid,但是uuid中存在-,如下图: 去除uuid的- 默认生成的uuid含有-,我们可以使用replace函数替换掉-,SQL如下 select replace(uuid(),"-","") as uuid;Insert语句中使用UUID 如果…...

包与字符串
包是分类管理的需要,建立包用:package,包中类的引用import 学习使用javaAPI中的字符串类String,学会其成员方法的使用 (必看)eclipse包的分层等级结构设置 因为eclipse的包的结构默认是平行等级的,所以要手…...
【Gradle】mac环境安装Gradle及配置
官网安装说明:Gradle | Installation 由于Gradle运行依赖jvm,所以事先需要安装jdk,并确认你的jdk版本和gradle版本要求的对应关系,这个官网上有说明,但是我试了一下不太准确,供参考,链接如下&a…...

使用C语言操作kafka ---- librdkafka
1 安装librdkafka git clone https://github.com/edenhill/librdkafka.git cd librdkafka git checkout v1.7.0 ./configure make sudo make install sudo ldconfig 在librdkafka的examples目录下会有示例程序。比如consumer的启动需要下列参数 ./consumer <broker> &…...
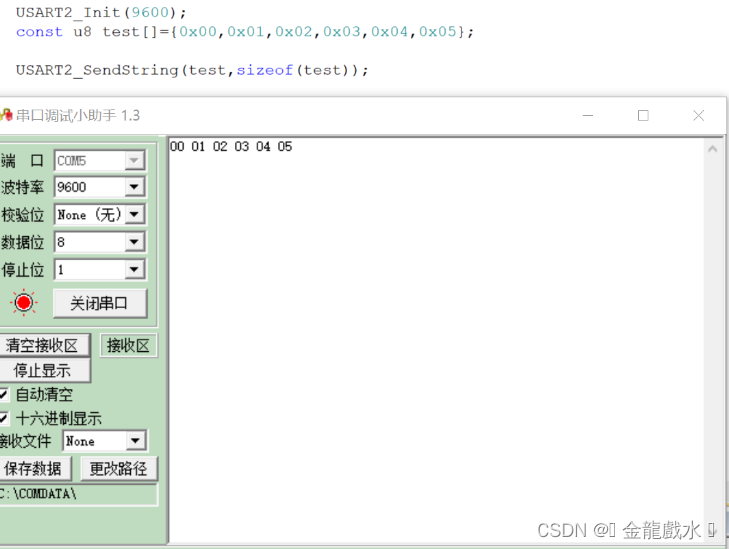
误用STM32串口发送标志位 “USART_FLAG_TXE” “USART_FLAG_TC”造成的BUG
当你使用串口发送数据时是否出现过这样的情况: 1.发送时第一个字节丢失。 2.发送时出现莫名的字节丢失。 3.各种情况字节丢失。 1.先了解一下串口发送的流程图(手动描绘): 可以假想USART_FLAG_TXE是用于检测"弹仓"&…...

指针(三)
函数指针 定义:整型指针是指向整形的指针,数组指针式指向数组的指针,其实函数指针就是指向函数的指针。 函数指针基础: ()优先级要高于*;一个变量除去了变量名,便是它的变量类型;一个指针变量…...

labelimg遇到的标签修改问题:修改一张图像的标签时,保存后导致classes.txt改变
问题描述:修改一张图像的标签时候, classes.txt 会同步更新,导致重新生成了 classes.txt 但是这个 classes.txt 只有你现在写的那个类别名,以前的没有了。 解决:设置一个 predefined_classes.txt,内容和模…...

Spring Cloud Gateway使用和配置
Spring Cloud Gateway是Spring官方基于Spring 5.0,Spring Boot 2.0和Project Reactor等技术开发的网关,Spring Cloud Gateway旨在为微服务架构提供一种简单而有效的统一的API路由管理方式。Spring Cloud Gateway作为Spring Cloud生态系中的网关ÿ…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...

Rust 开发环境搭建
环境搭建 1、开发工具RustRover 或者vs code 2、Cygwin64 安装 https://cygwin.com/install.html 在工具终端执行: rustup toolchain install stable-x86_64-pc-windows-gnu rustup default stable-x86_64-pc-windows-gnu 2、Hello World fn main() { println…...
