当前位置： 首页 > news >正文

《点云进阶》专栏文章目录

news 2026/2/7 15:44:36

目录

  • 一、PCL进阶篇
    • *
  • 二、Open3D进阶篇

一、PCL进阶篇

*

  • PCL 最小二乘拟合二维直线
  • PCL 最小二乘拟合空间直线
  • PCL 计算点云的倒角距离（Chamfer Distance）
  • PCL 点云配准精度评价——点到面的均方根误差
  • PCL 可视化八叉树
  • PCL 计算Hausdorff距离
  • PCL 从变换矩阵中提取欧拉角
  • PCL 点云中值滤波(适用于所有点云)
  • PCL 点云均值滤波
  • PCL 点云切片
  • PCL 求两平面的交线
  • PCL 批量处理点云
  • PCL 三点确定一个平面原理及代码实现
  • PCL 精确计算八叉树占用体素的中心点
  • PCL 从给定的平移和欧拉角创建变换矩阵
  • PCL 点云Delaunay三角剖分
  • PCL 点云Z-Score 标准化
  • PCL 大场景点云水平面校准
  • PCL 计算点云各字段数据的均值
  • PCL 计算USC并可视化
  • PCL RANSAC实现点云粗配准(无需特征描述子)
  • PCL 基于6D协方差的点云采样
  • PCL 计算点云的几何特征
  • PCL计算点云粗糙度
  • PCL 最小二乘拟合二维圆
  • PCL 最小二乘拟合二次曲面
  • PCL 最小二乘拟合多项式曲线
  • PCL 点云分块
  • PCL CSF布料模拟算法
  • PCL 点云转彩色图像
  • PCL 从给定的变换矩阵中提取欧拉角和平移向量
  • PCL DBSCAN密度聚类
  • PCL 点云导向滤波(Guided Filter)
  • PCL 点云按时间进行分段
  • PCL 法线定向
  • PCL 计算三个互不平行平面的交点
  • PCL 方向向量约束的改进ICP算法
  • PCL 基于法向量夹角的点云特征点提取(重制，增强版)
  • PCL 点云镜像变换
  • PCL 最小中值平方法拟合平面
  • PCL 计算点云包围球
  • PCL 点云按比率随机采样
  • PCL 计算平面三角形外接圆的圆心和半径
  • PCL 点云包围球内添加均匀分布的随机噪声添加链接描述
  • PCL 从模型数据中均匀采样点云
  • PCL 改进统计滤波
  • PCL 最小二乘拟合空间曲线
  • PCL 计算两空间直线的交点
  • PCL 点云沿坐标轴进行等距切片
  • PCL 机载点云电力线提取
  • PCL Kmeans点云聚类
  • PCL 基于投影点密度的建筑物立面提取
  • PCL 道格拉斯—普克节点抽稀算法(C++详细过程版)
  • PCL 条件欧式聚类分割
  • PCL 平面点云边界点按顺/逆时针排序(方法二)
  • PCL 点云绕任意点旋转
  • PCL Super4PCS算法实现点云粗配准（版本一）
  • PCL Super4PCS算法实现点云粗配准（版本二）
  • PCL 点云生成DSM
  • PCL 使用点云创建数字高程模型DEM
  • PCL 使用点云构建不规则三角网TIN
  • PCL 点云转强度图像（方法二）
  • 【论文复现】——FEC: Fast Euclidean Clustering for Point Cloud Segmentation
  • 【论文复现】——基于逐点前进法的点云数据精简
  • PCL 计算空间直线与平面的交点
  • 【论文复现】 一种基于栅格投影的快速地面点云分割算法
  • 【论文复现】——Patchwork++：基于点云的快速稳健地面分割方法
  • PCL 动态半径滤波
  • PCL RANSAC拟合圆柱——提取圆柱体的中轴线
  • PCL RANSAC拟合圆柱——计算圆柱的体积和表面积
  • PCL 最小生成树用于法向量定向
  • PCL 计算四面体的体积
  • PCL 欧式聚类分割高阶用法——获取最大聚类
  • PCL 法向量夹角约束的欧式聚类分割
  • PCL 改进快速欧式聚类
  • PCL 法向量约束的4PCS配准算法
  • 【论文复现】—— 基于最小平方中值的点云平面拟合算法
  • PCL 算法各阶段运行效率统计
  • PCL Kmeans++点云聚类
  • PCL 偏度平衡滤波(SKF)算法
  • PCL 基于迭代双边滤波的点云平滑
  • PCL 间接平差法拟合平面
  • PCL 间接平差法拟合二维直线
  • PCL 计算给定点位的坡度
  • PCL 计算空间三角形的面积
  • PCL .pcd点云快速转.txt格式
  • PCL 读取.pts格式点云并可视化
  • PCL 建筑物点云立面和平面分割提取
  • PCL RANSAC分割多个平面（方法二）
  • PCL 计算点云粗糙度（方法二）
  • PCL 计算点云粗糙度（方法三）
    在这里插入图片描述

二、Open3D进阶篇

  • Open3D 进阶（1） MeanShift点云聚类
  • Open3D 进阶（2）DBSCAN点云聚类
  • Open3D 进阶（3）OPTICS点云聚类
  • Open3D 进阶（4）高斯混合点云聚类
  • Open3D 进阶（5）变分贝叶斯高斯混合点云聚类
  • Open3D 进阶（6）Kmeans点云聚类
  • Open3D 进阶（7）Kmeans++点云聚类
  • Open3D 进阶（8）小批量 KMeans点云聚类
  • Open3D 进阶（9）使用BCPD算法对点云配准
  • Open3D 进阶（10）使用FilterReg算法对点云配准
  • Open3D 进阶（11）使用GMM-Tree算法对点云配准
  • Open3D 进阶（12）PCA拟合平面
  • Open3D 进阶（13）使用PCA将点云投影到主成分空间
  • Open3D 进阶（14）PCA拟合空间直线
  • Open3D 进阶（15）方向向量约束的PCA快速粗配准
  • Open3D 进阶（16）三维点云边界提取
  • Open3D 进阶（17）间接平差拟合二维直线
  • Open3D 进阶（18）整体最小二乘拟合平面
  • Open3D 进阶（19）间接平差法拟合平面

相关文章：

《点云进阶》专栏文章目录

目录 一、PCL进阶篇* 二、Open3D进阶篇 一、PCL进阶篇 * PCL 最小二乘拟合二维直线PCL 最小二乘拟合空间直线PCL 计算点云的倒角距离（Chamfer Distance）PCL 点云配准精度评价——点到面的均方根误差PCL 可视化八叉树PCL 计算Hausdorff距离PCL 从变换矩…...

编程日记 2023/12/7 10:24:39

二分查找算法-查找最接近的元素Python实现（题目来源dotcpp: 2926）

题目描述 在一个非降序列中&#xff0c;查找与给定值最接近的元素。 输入格式 第一行包含一个整数n&#xff0c;为非降序列长度。1 < n < 100000。 第二行包含n个整数&#xff0c;为非降序列各元素。所有元素的大小均在0-1,000,000,000之间。 第三行包含一个整数m&#x…...

编程日记 2023/12/7 10:23:38

debian11,debian 如何删除虚拟内存,交换分区

1.以管理员身份登录系统 2.输入以下命令以删除虚拟内存,该命令将关闭当前正在使用的虚拟内存。 sudo swapoff -a 3.输入以下命令以永久删除虚拟内存(硬盘内存文件)&#xff1a; sudo rm /swapfile 4.重启系统 总结:以上步骤将删除 Debian 11 中的虚拟内存。请注意&#xf…...

编程日记 2023/12/7 10:20:35

智能优化算法应用：基于人工大猩猩部队算法无线传感器网络(WSN)覆盖优化 - 附代码

智能优化算法应用&#xff1a;基于人工大猩猩部队算法无线传感器网络(WSN)覆盖优化 - 附代码 文章目录 智能优化算法应用&#xff1a;基于人工大猩猩部队算法无线传感器网络(WSN)覆盖优化 - 附代码1.无线传感网络节点模型2.覆盖数学模型及分析3.人工大猩猩部队算法4.实验参数设…...

编程日记 2023/12/7 10:16:32

鼎捷受邀出席“中国制造业产品创新数字化国际峰会”，共话工业软件创新发展

11月30日&#xff0c; 由e-works数字化企业网、四川省智能制造创新中心、重庆制信信息技术服务有限公司主办的第十九届中国制造业产品创新数字化国际峰会在四川成都盛大开幕。 作为制造业研发信息化领域规模、影响力兼具的专业论坛&#xff0c;本届峰会以“构建基于数字底座的…...

编程日记 2023/12/7 10:15:31

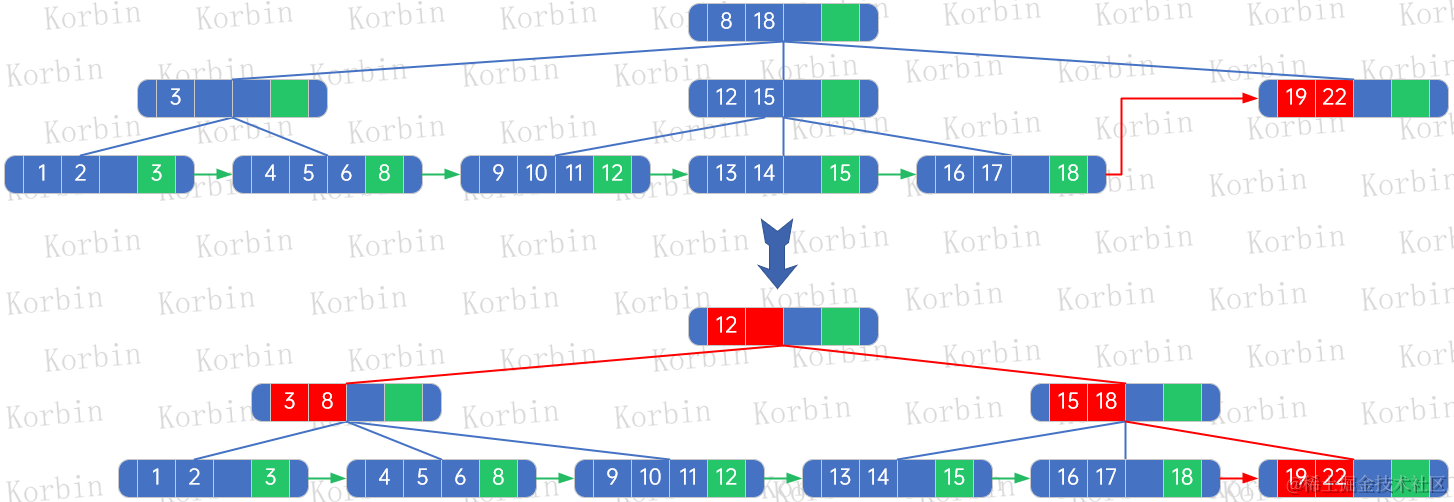
大话数据结构-查找-多路查找树

注&#xff1a;本文同步发布于稀土掘金。 7 多路查找树 多路查找树&#xff08;multi-way search tree&#xff09;&#xff0c;其每个结点的孩子可以多于两个&#xff0c;且每一个结点处可以存储多个元素。由于它是查找树&#xff0c;所有元素之间存在某种特定的排序关系。 …...

编程日记 2023/12/7 10:11:23

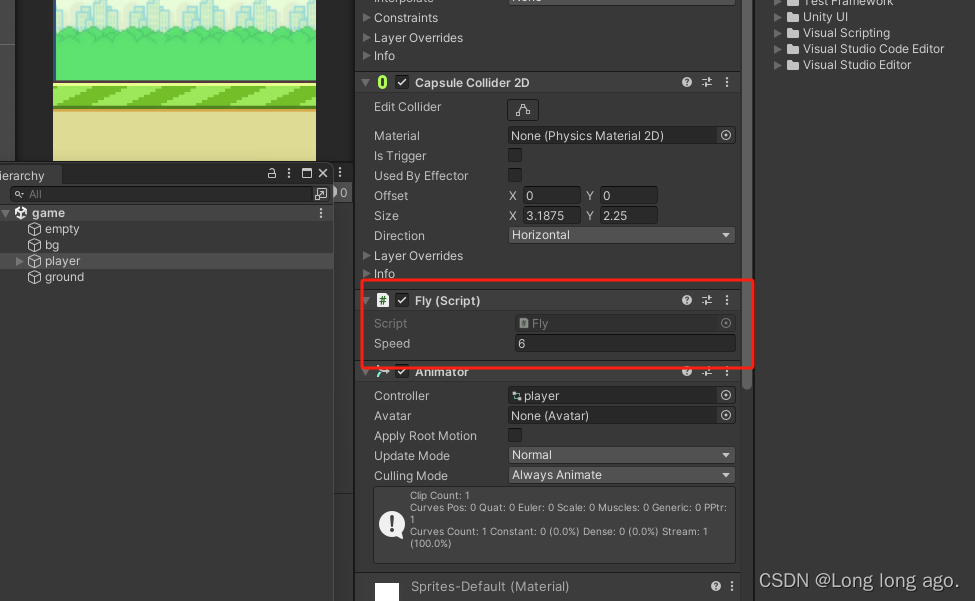
unity 2d 入门 飞翔小鸟 飞翔脚本（五)

新建c#脚本 using System.Collections; using System.Collections.Generic; using UnityEngine;public class Fly : MonoBehaviour {//获取小鸟&#xff08;刚体&#xff09;private Rigidbody2D bird;//速度public float speed;// Start is called before the first frame up…...

编程日记 2023/12/7 10:10:22

Linux系统调试课：I2C tools调试工具

文章目录 一、如何使用I2C tools测试I2C外设1、I2C tools概述： 2、下载I2C tools源码：3、编译I2C tools源码： 4、i2cdetect 5、i2cget 6、i2cdump...

编程日记 2023/12/7 10:09:21

uniapp中解决swiper高度自适应内容高度

起因&#xff1a;uniapp中swiper组件swiper 标签存在默认高度是 height: 150px &#xff1b;高度无法实现由内容撑开&#xff0c;在默认情况下&#xff0c;swiper盒子高度显示总是 150px 解决办法思路&#xff1a; 动态设置swiper盒子的高度&#xff0c;故需要获取swiper-item盒…...

编程日记 2023/12/7 10:07:19

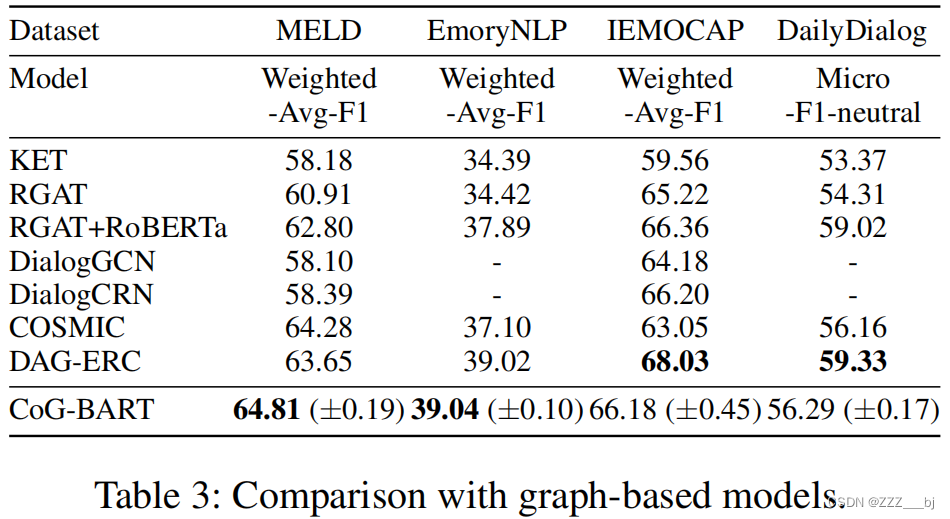
Contrast and Generation Make BART a Good Dialogue Emotion Recognizer

摘要 在对话系统中&#xff0c;具有相似语义的话语在不同的语境下可能具有不同的情感。因此&#xff0c;用说话者依赖来建模长期情境情绪关系在对话情绪识别中起着至关重要的作用。同时&#xff0c;区分不同的情绪类别也不是很简单的&#xff0c;因为它们通常具有语义上相似的…...

编程日记 2023/12/7 10:06:18

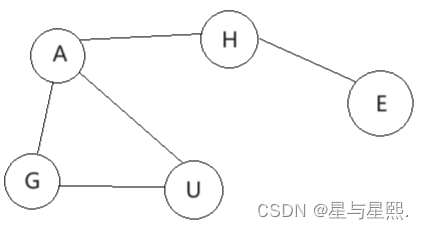
图的深度优先搜索(数据结构实训)

题目&#xff1a; 图的深度优先搜索 描述&#xff1a; 图的深度优先搜索类似于树的先根遍历&#xff0c;是树的先根遍历的推广。即从某个结点开始&#xff0c;先访问该结点&#xff0c;然后深度访问该结点的第一棵子树&#xff0c;依次为第二顶子树。如此进行下去&#xff0c;直…...

编程日记 2023/12/7 10:01:14

VUEX使用总结

1、Store 使用 文件内容大概就是这三个。通俗来讲actions负责向后端获取数据的&#xff0c;内部执行异步操作分发 Action&#xff0c;调用commit提交一个 mutation。 mutations通过Action提交commit的数据进行提交荷载&#xff0c;使state有数据。 vuex的数据是共享的&#xf…...

编程日记 2023/12/7 9:58:12

指定分隔符对字符串进行分割 numpy.char.split()

【小白从小学Python、C、Java】 【计算机等考500强证书考研】 【Python-数据分析】 指定分隔符对字符串进行分割 numpy.char.split() 选择题 请问下列程序运行的的结果是&#xff1a; import numpy as np print("【执行】np.char.split(I.Love.China, sep .)") p…...

编程日记 2023/12/7 9:56:10

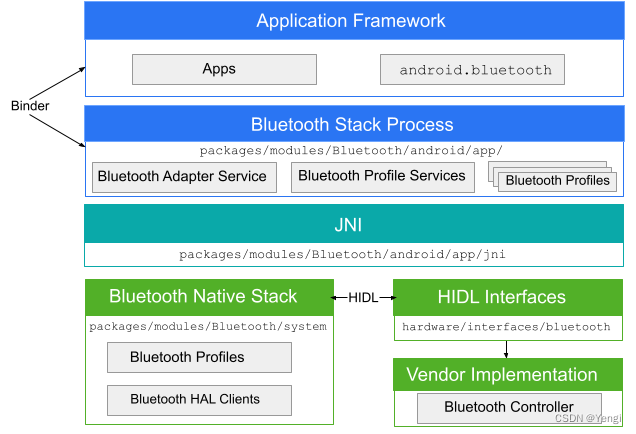
Android12蓝牙框架

参考&#xff1a; https://evilpan.com/2021/07/11/android-bt/ https://source.android.com/docs/core/connect/bluetooth?hlzh-cn https://developer.android.com/guide/topics/connectivity/bluetooth?hlzh-cn https://developer.android.com/guide/components/intents-fi…...

编程日记 2023/12/7 9:52:07

python文件docx转pdf

centos部署的django项目&#xff0c;使用libreoffice做文件转换&#xff0c;官网给环境安装好libreoffice后&#xff0c;可使用命令行来进行转化 还可转换其他的各种格式&#xff0c;本文只做了pdf转换 import subprocess import os def convert_to_pdf(input_file, o…...

编程日记 2023/12/7 9:51:06

9.基于SpringBoot3+I18N实现国际化

1. 新建资源文件 在resources目录下新建目录i18n, 然后 新建messages_en.properties文件 user.login.erroraccount or password error&#xff01;新建messages_zh_CN.properties文件 user.login.error帐户或密码错误&#xff01;2. 新建LocaleConfig.java文件 Configurati…...

编程日记 2023/12/7 9:50:05

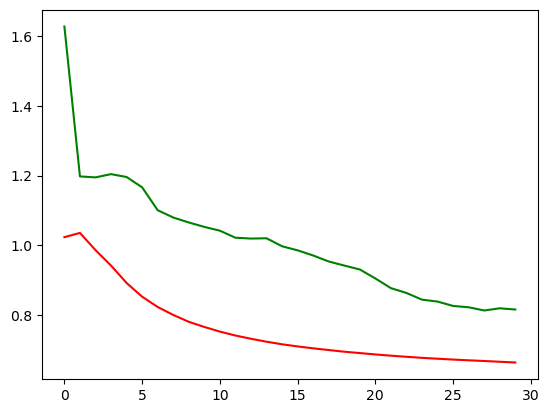
27. 深度学习进阶 - 为什么RNN

文章目录 一个柯基的例子为什么RNN or CNN Hi&#xff0c;你好。我是茶桁。 这节课开始&#xff0c;我们将会讲一个比较重要的一种神经网络&#xff0c;它对应了咱们整个生活中很多类型的一种问题结构&#xff0c;它就是咱们的RNN网络。 咱们首先回忆一下&#xff0c;上节课咱…...

编程日记 2023/12/7 9:48:03

谈一谈柔性数组

文章目录 什么是柔性数组柔性数组有什么用 什么是柔性数组 柔性数组是一种动态可变的数组&#xff0c;也许你从来没有听说过这个概念&#xff0c;但是它确实是存在的&#xff0c;是在C99标准底下支持的一种语法。想要使用柔性数组需要满足3个条件&#xff1a; 柔性数组只能存在…...

编程日记 2023/12/7 9:46:00

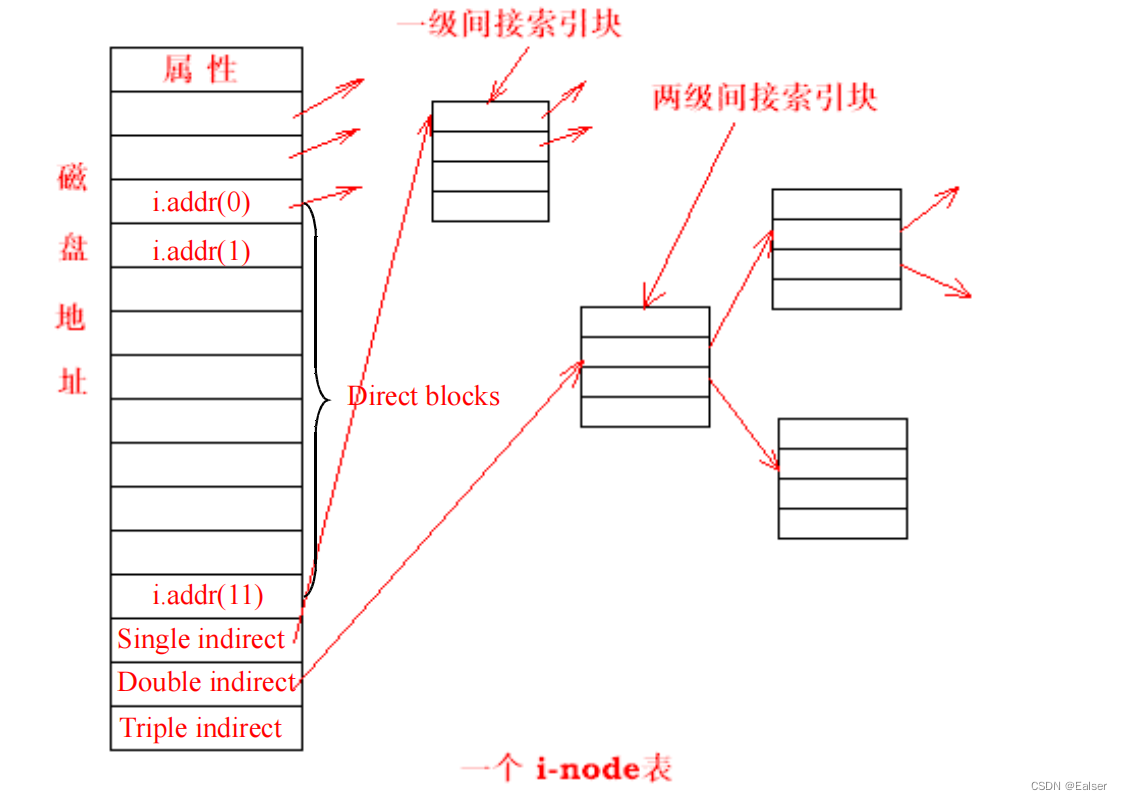
＜Linux＞（极简关键、省时省力）《Linux操作系统原理分析之Linux文件管理（1）》（25）

《Linux操作系统原理分析之Linux文件管理&#xff08;1&#xff09;》&#xff08;25&#xff09; 8 Linux文件管理8.1 Linux 文件系统概述8.2 EXT2 文件系统8.2.1 EXT2 文件系统的构造8.2.2 EXT2 超级块&#xff08;super block&#xff09;8.2.3 组描述符8.2.4 块位图 8.3 EX…...

编程日记 2023/12/7 9:43:59

算能PCIe开发环境搭建-一些记录

开发环境与运行环境&#xff1a; 开发环境是指用于模型转换或验证以及程序编译等开发过程的环境&#xff1b;运行环境是指在具备Sophon设备的平台上实际使用设备进行算法应用部署的运行环境。 开发环境与运行环境可能是统一的&#xff08;如插有SC5加速卡的x86主机&#xff0c;…...

编程日记 2023/12/7 9:34:50

synchronized 学习

学习源&#xff1a; https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖&#xff0c;也要考虑性能问题&#xff08;场景&#xff09; 2.常见面试问题&#xff1a; sync出…...

编程新知 2025/12/14 17:38:17

镜像里切换为普通用户

如果你登录远程虚拟机默认就是 root 用户&#xff0c;但你不希望用 root 权限运行 ns-3&#xff08;这是对的&#xff0c;ns3 工具会拒绝 root&#xff09;&#xff0c;你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案&#xff1a;创建非 roo…...

编程新知 2025/9/11 11:00:29

【RockeMQ】第2节｜RocketMQ快速实战以及核⼼概念详解（二）

升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点&#xff0c;但无自动故障转移能力&#xff0c;Master宕机后需人工切换&#xff0c;期间消息可能无法读取。Slave仅存储数据&#xff0c;无法主动升级为Master响应请求&#xff…...

编程新知 2025/9/2 3:37:40

3403. 从盒子中找出字典序最大的字符串 I

3403. 从盒子中找出字典序最大的字符串 I 题目链接&#xff1a;3403. 从盒子中找出字典序最大的字符串 I 代码如下&#xff1a; class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

编程新知 2025/10/31 5:18:02

爬虫基础学习day2

# 爬虫设计领域 工商&#xff1a;企查查、天眼查短视频&#xff1a;抖音、快手、西瓜 ---> 飞瓜电商&#xff1a;京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空&#xff1a;抓取所有航空公司价格 ---> 去哪儿自媒体&#xff1a;采集自媒体数据进…...

编程新知 2025/12/5 3:38:11

高防服务器能够抵御哪些网络攻击呢？

高防服务器作为一种有着高度防御能力的服务器&#xff0c;可以帮助网站应对分布式拒绝服务攻击&#xff0c;有效识别和清理一些恶意的网络流量&#xff0c;为用户提供安全且稳定的网络环境&#xff0c;那么&#xff0c;高防服务器一般都可以抵御哪些网络攻击呢&#xff1f;下面…...

编程新知 2025/9/3 19:14:38

ui框架-文件列表展示

ui框架-文件列表展示 介绍 UI框架的文件列表展示组件&#xff0c;可以展示文件夹&#xff0c;支持列表展示和图标展示模式。组件提供了丰富的功能和可配置选项&#xff0c;适用于文件管理、文件上传等场景。 功能特性 支持列表模式和网格模式的切换展示支持文件和文件夹的层…...

编程新知 2026/2/4 17:34:02

【免费数据】2005-2019年我国272个地级市的旅游竞争力多指标数据（33个指标）

旅游业是一个城市的重要产业构成。旅游竞争力是一个城市竞争力的重要构成部分。一个城市的旅游竞争力反映了其在旅游市场竞争中的比较优势。 今日我们分享的是2005-2019年我国272个地级市的旅游竞争力多指标数据&#xff01;该数据集源自2025年4月发表于《地理学报》的论文成果…...

编程新知 2026/1/26 19:23:28

深入浅出WebGL：在浏览器中解锁3D世界的魔法钥匙

WebGL&#xff1a;在浏览器中解锁3D世界的魔法钥匙 引言&#xff1a;网页的边界正在消失 在数字化浪潮的推动下&#xff0c;网页早已不再是静态信息的展示窗口。如今&#xff0c;我们可以在浏览器中体验逼真的3D游戏、交互式数据可视化、虚拟实验室&#xff0c;甚至沉浸式的V…...

编程新知 2025/10/31 9:08:31

命令行关闭Windows防火墙

命令行关闭Windows防火墙 引言一、防火墙：被低估的"智能安检员"二、优先尝试！90%问题无需关闭防火墙方案1：程序白名单（解决软件误拦截）方案2：开放特定端口（解决网游/开发端口不通）三、命令行极速关闭方案方法一：PowerShell（推荐Win10/11）​方法二：CMD命令…...

编程新知 2025/8/27 20:07:03