[linux] 输出文本文件的最后一列并去重
使用 awk 命令来实现这个需求。下面是一个示例命令:
awk -F ',' '{print $NF}' a.txt | sort -u
解释一下这个命令:
awk -F ',' '{print $NF}' a.txt:使用逗号作为字段分隔符(-F ','),打印每行的最后一个字段($NF)。sort -u:对输出结果进行排序并去重,只输出不重复的最后一个字段。
假设 a.txt 文件内容如下:
apple,banana,orange
orange,grape,apple
banana,apple,pear
运行上述命令后,将输出以下结果:
orange
apple
pear
相关文章:

[linux] 输出文本文件的最后一列并去重
使用 awk 命令来实现这个需求。下面是一个示例命令: awk -F , {print $NF} a.txt | sort -u解释一下这个命令: awk -F , {print $NF} a.txt:使用逗号作为字段分隔符(-F ,),打印每行的最后一个字段&#x…...
新能源车交直流充电解释
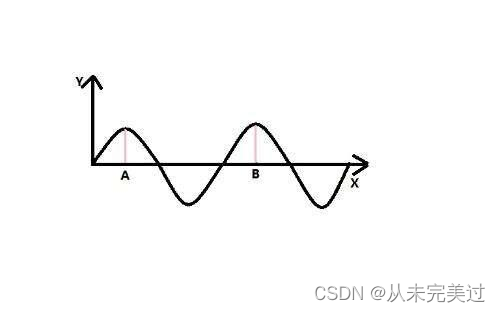
交流充电: 国家电网输出的电都是交流电,如下图所示,具有正弦切换规律的 而电动车的电池只能接受直流电,因此需要首先把交流电转换成直流电才能充进汽车电池,这就需要到了转换器OBC(on-board Charger&#…...

Failed to connect to gitee.com port 443: Time out 连接超时提示【Bug已完美解决-鸿蒙开发】
文章目录 项目场景:问题描述原因分析:解决方案:解决方案1解决方案2:解决方案3:此Bug解决方案总结解决方案总结**心得体会:解决连接超时问题的三种方案**项目场景: 导入Sample时遇到导入失败的情况,并提示“Failed to connect to gitee.com port 443: Time out”连接超…...

【开源】基于Vue+SpringBoot的智慧家政系统
项目编号: S 063 ,文末获取源码。 \color{red}{项目编号:S063,文末获取源码。} 项目编号:S063,文末获取源码。 目录 一、摘要1.1 项目介绍1.2 项目录屏 二、功能模块三、系统展示四、核心代码4.1 查询家政服…...
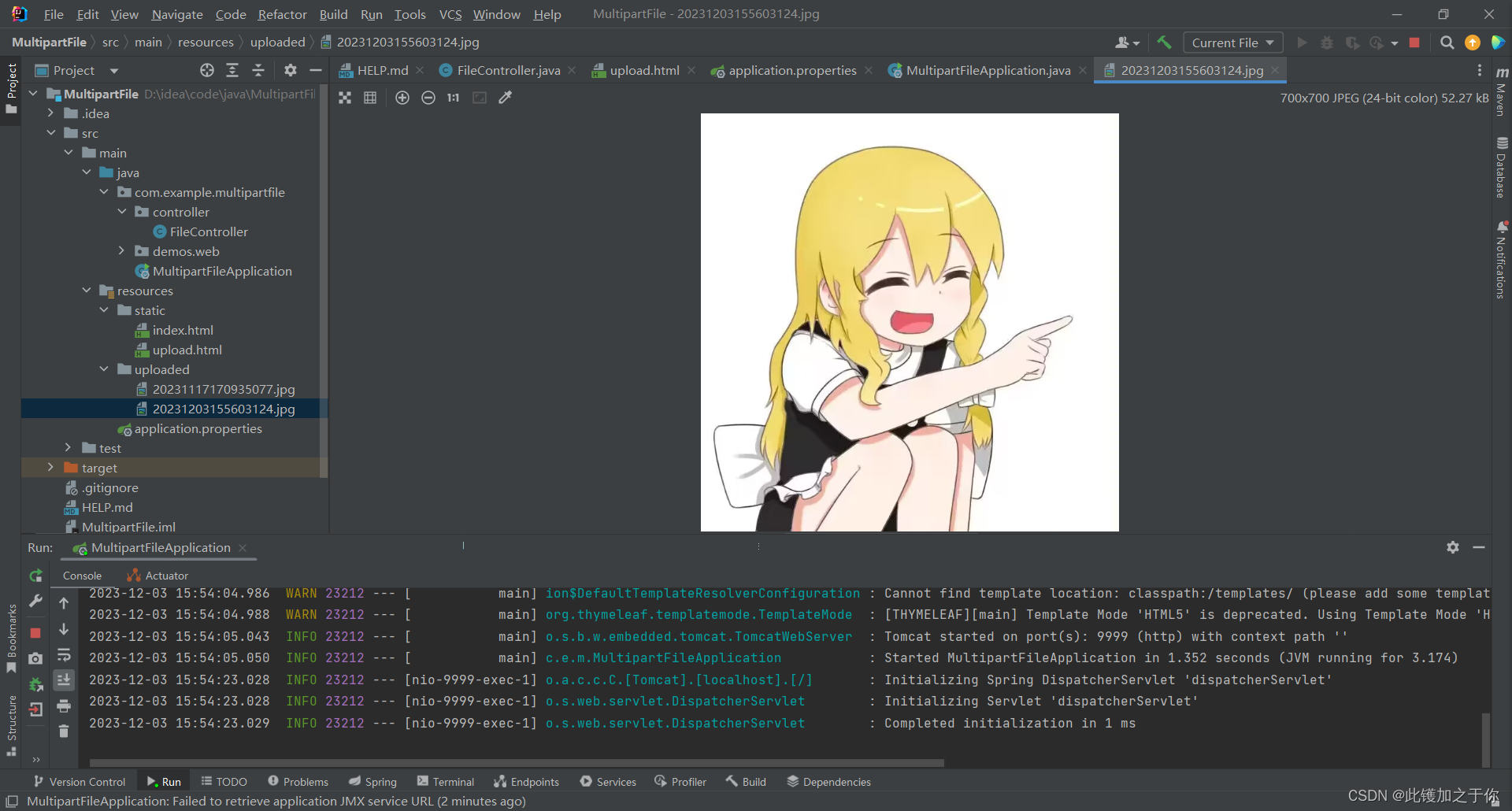
javaee实验:文件上传及拦截器的使用
目录 文件上传ModelAttribute注解实验目的实验内容实验过程项目结构编写代码结果展示 文件上传 Spring MVC 提供 MultipartFile 接口作为参数来处理文件上传。 MultipartFile 提供以下方法来获取上传的文件信息: getOriginalFilename 获取上传的文件名字&#x…...
-1)
二分查找19(Leetcode540有序数组中的单一元素)-1
代码: 没用二分查找版: class Solution {public int singleNonDuplicate(int[] nums) {if(nums.length1){return nums[0];}for(int i1;i<nums.length-1;i){if(nums[i-1]nums[i]||nums[i]nums[i1]){continue;}else{return nums[i];}}if(nums[0]nums[…...
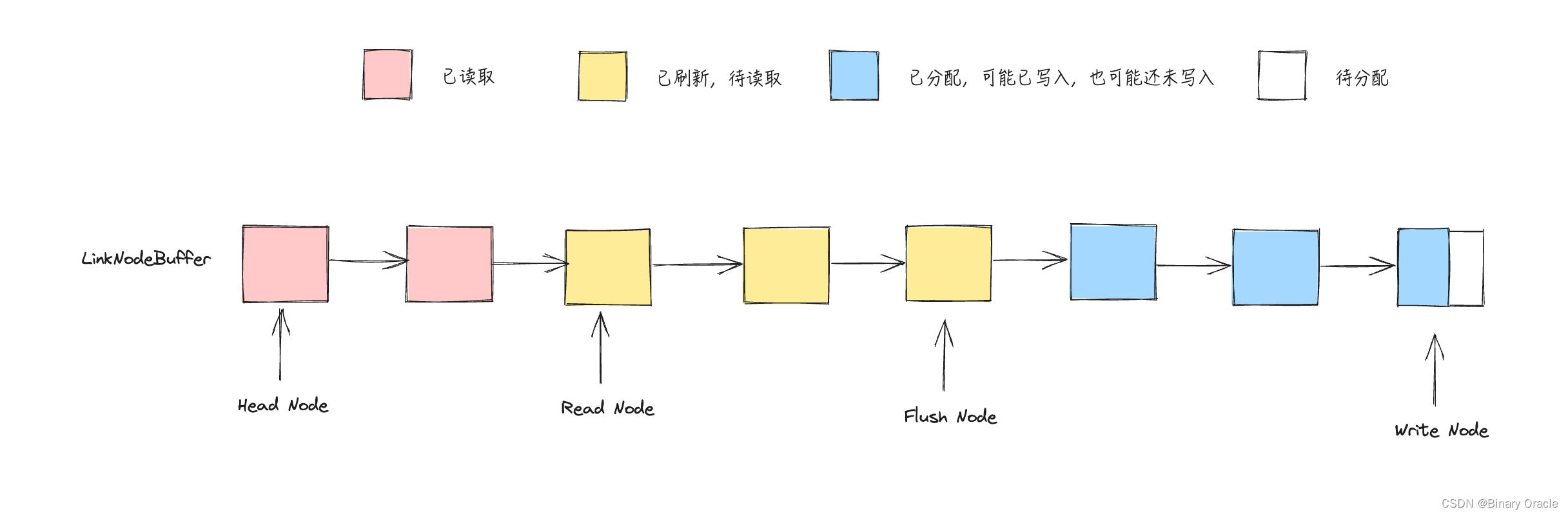
字节开源的netPoll底层LinkBuffer设计与实现
字节开源的netPoll底层LinkBuffer设计与实现 为什么需要LinkBuffer介绍设计思路数据结构LinkBufferNodeAPI LinkBuffer读 API写 APIbook / bookAck api 小结 本文基于字节开源的NetPoll版本进行讲解,对应官方文档链接为: Netpoll对应官方文档链接 netPoll底层有一个…...

《点云进阶》专栏文章目录
目录 一、PCL进阶篇* 二、Open3D进阶篇 一、PCL进阶篇 * PCL 最小二乘拟合二维直线PCL 最小二乘拟合空间直线PCL 计算点云的倒角距离(Chamfer Distance)PCL 点云配准精度评价——点到面的均方根误差PCL 可视化八叉树PCL 计算Hausdorff距离PCL 从变换矩…...
)
二分查找算法-查找最接近的元素Python实现(题目来源dotcpp: 2926)
题目描述 在一个非降序列中,查找与给定值最接近的元素。 输入格式 第一行包含一个整数n,为非降序列长度。1 < n < 100000。 第二行包含n个整数,为非降序列各元素。所有元素的大小均在0-1,000,000,000之间。 第三行包含一个整数m&#x…...

debian11,debian 如何删除虚拟内存,交换分区
1.以管理员身份登录系统 2.输入以下命令以删除虚拟内存,该命令将关闭当前正在使用的虚拟内存。 sudo swapoff -a 3.输入以下命令以永久删除虚拟内存(硬盘内存文件): sudo rm /swapfile 4.重启系统 总结:以上步骤将删除 Debian 11 中的虚拟内存。请注意…...

智能优化算法应用:基于人工大猩猩部队算法无线传感器网络(WSN)覆盖优化 - 附代码
智能优化算法应用:基于人工大猩猩部队算法无线传感器网络(WSN)覆盖优化 - 附代码 文章目录 智能优化算法应用:基于人工大猩猩部队算法无线传感器网络(WSN)覆盖优化 - 附代码1.无线传感网络节点模型2.覆盖数学模型及分析3.人工大猩猩部队算法4.实验参数设…...

鼎捷受邀出席“中国制造业产品创新数字化国际峰会”,共话工业软件创新发展
11月30日, 由e-works数字化企业网、四川省智能制造创新中心、重庆制信信息技术服务有限公司主办的第十九届中国制造业产品创新数字化国际峰会在四川成都盛大开幕。 作为制造业研发信息化领域规模、影响力兼具的专业论坛,本届峰会以“构建基于数字底座的…...
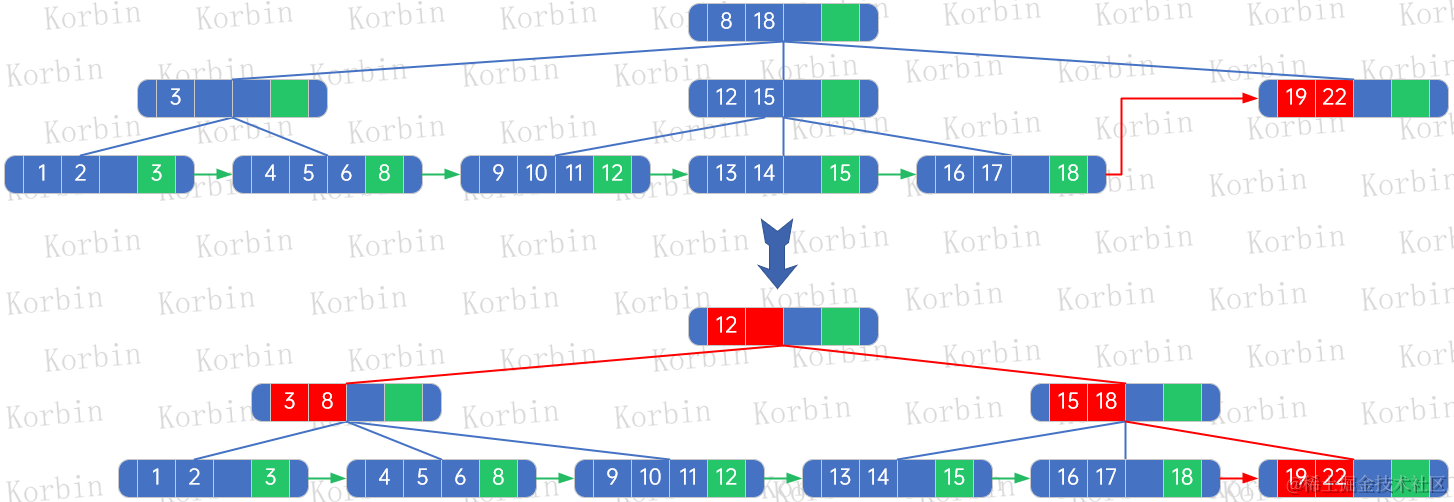
大话数据结构-查找-多路查找树
注:本文同步发布于稀土掘金。 7 多路查找树 多路查找树(multi-way search tree),其每个结点的孩子可以多于两个,且每一个结点处可以存储多个元素。由于它是查找树,所有元素之间存在某种特定的排序关系。 …...
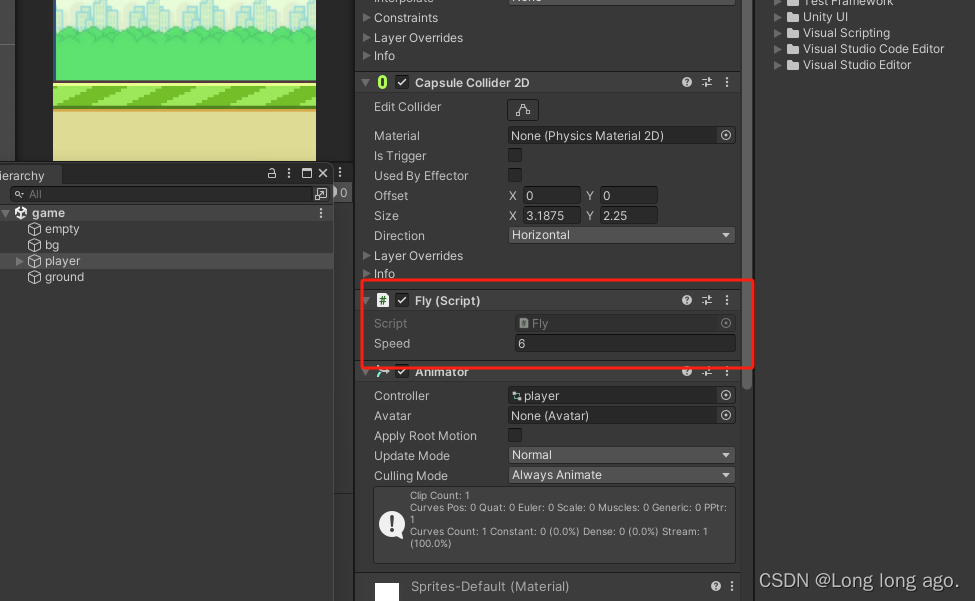
unity 2d 入门 飞翔小鸟 飞翔脚本(五)
新建c#脚本 using System.Collections; using System.Collections.Generic; using UnityEngine;public class Fly : MonoBehaviour {//获取小鸟(刚体)private Rigidbody2D bird;//速度public float speed;// Start is called before the first frame up…...
Linux系统调试课:I2C tools调试工具
文章目录 一、如何使用I2C tools测试I2C外设1、I2C tools概述: 2、下载I2C tools源码:3、编译I2C tools源码: 4、i2cdetect 5、i2cget 6、i2cdump...
uniapp中解决swiper高度自适应内容高度
起因:uniapp中swiper组件swiper 标签存在默认高度是 height: 150px ;高度无法实现由内容撑开,在默认情况下,swiper盒子高度显示总是 150px 解决办法思路: 动态设置swiper盒子的高度,故需要获取swiper-item盒…...
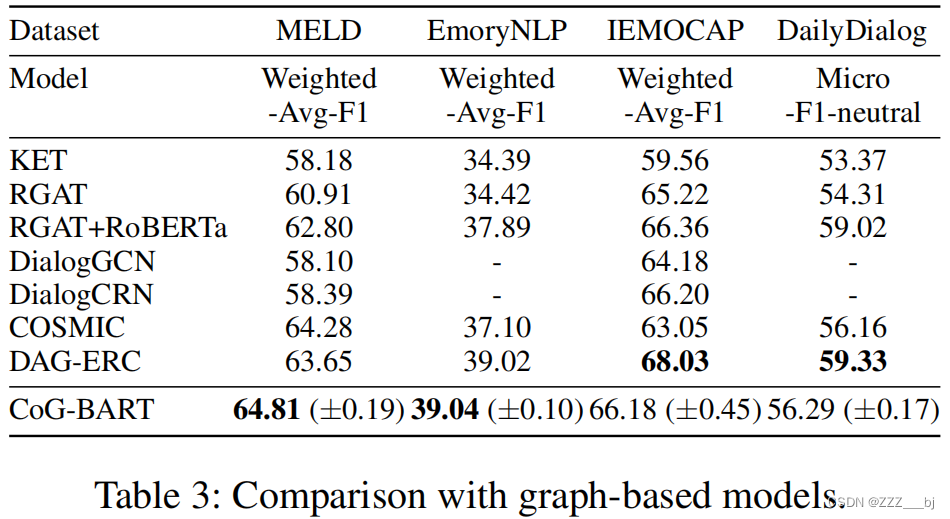
Contrast and Generation Make BART a Good Dialogue Emotion Recognizer
摘要 在对话系统中,具有相似语义的话语在不同的语境下可能具有不同的情感。因此,用说话者依赖来建模长期情境情绪关系在对话情绪识别中起着至关重要的作用。同时,区分不同的情绪类别也不是很简单的,因为它们通常具有语义上相似的…...
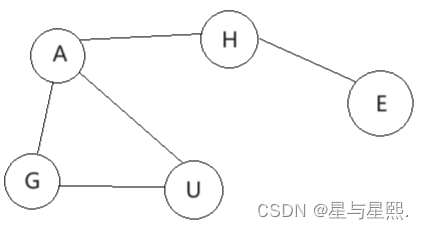
图的深度优先搜索(数据结构实训)
题目: 图的深度优先搜索 描述: 图的深度优先搜索类似于树的先根遍历,是树的先根遍历的推广。即从某个结点开始,先访问该结点,然后深度访问该结点的第一棵子树,依次为第二顶子树。如此进行下去,直…...

VUEX使用总结
1、Store 使用 文件内容大概就是这三个。通俗来讲actions负责向后端获取数据的,内部执行异步操作分发 Action,调用commit提交一个 mutation。 mutations通过Action提交commit的数据进行提交荷载,使state有数据。 vuex的数据是共享的…...

指定分隔符对字符串进行分割 numpy.char.split()
【小白从小学Python、C、Java】 【计算机等考500强证书考研】 【Python-数据分析】 指定分隔符对字符串进行分割 numpy.char.split() 选择题 请问下列程序运行的的结果是: import numpy as np print("【执行】np.char.split(I.Love.China, sep .)") p…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

USB Over IP专用硬件的5个特点
USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中,从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备(如专用硬件设备),从而消除了直接物理连接的需要。USB over IP的…...

在 Spring Boot 中使用 JSP
jsp? 好多年没用了。重新整一下 还费了点时间,记录一下。 项目结构: pom: <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://ww…...

【SpringBoot自动化部署】
SpringBoot自动化部署方法 使用Jenkins进行持续集成与部署 Jenkins是最常用的自动化部署工具之一,能够实现代码拉取、构建、测试和部署的全流程自动化。 配置Jenkins任务时,需要添加Git仓库地址和凭证,设置构建触发器(如GitHub…...

c# 局部函数 定义、功能与示例
C# 局部函数:定义、功能与示例 1. 定义与功能 局部函数(Local Function)是嵌套在另一个方法内部的私有方法,仅在包含它的方法内可见。 • 作用:封装仅用于当前方法的逻辑,避免污染类作用域,提升…...

《Docker》架构
文章目录 架构模式单机架构应用数据分离架构应用服务器集群架构读写分离/主从分离架构冷热分离架构垂直分库架构微服务架构容器编排架构什么是容器,docker,镜像,k8s 架构模式 单机架构 单机架构其实就是应用服务器和单机服务器都部署在同一…...

Visual Studio Code 扩展
Visual Studio Code 扩展 change-case 大小写转换EmmyLua for VSCode 调试插件Bookmarks 书签 change-case 大小写转换 https://marketplace.visualstudio.com/items?itemNamewmaurer.change-case 选中单词后,命令 changeCase.commands 可预览转换效果 EmmyLua…...

链式法则中 复合函数的推导路径 多变量“信息传递路径”
非常好,我们将之前关于偏导数链式法则中不能“约掉”偏导符号的问题,统一使用 二重复合函数: z f ( u ( x , y ) , v ( x , y ) ) \boxed{z f(u(x,y),\ v(x,y))} zf(u(x,y), v(x,y)) 来全面说明。我们会展示其全微分形式(偏导…...
