R语言进行正态分布检验
查了很多资料,还是比较模糊
Kolmogorov-Smirnov检验(K-S检验)广泛用于正态性检验和其他分布的拟合检验。适用于中等到大样本。
Lilliefors检验是K-S检验的一种变体,专门为小样本设计。其通过使用更准确的临界值来提高对小样本的适应性。
Shapiro-Wilk(S-W)检验通常在小样本下表现较好,而在大样本下可能对正态性的敏感性降低。在小样本情况下通常比K-S检验更准确。对于大样本,由于S-W检验可能会过于严格,导致拒绝正态性的可能性较大,这种情况下,应该使用K-S检验。
SPSS 5000及以下用Lilliefors检验、S-W检验;5000以上仅用Lilliefors检验
样本量>30时,倾向于看K-S检验结果;样本量≤30时,倾向于看Lilliefors检验、S-W检验结果
K-S检验
ks_result <- ks.test(sample_data, "pnorm")ks_result <- ks.test(sample_data, "pnorm", mean = mean(sample_data), sd = sd(sample_data))
S-W检验
shapiro_result <- shapiro.test(sample_data)
lillie修正的K-S检验
需要先安装
install.packages("nortest")
library(nortest)
lillie_result <- lillie.test(sample_data)
读取excel数据
library(readxl)
excel_file <- “数据分析测试数据.xlsx”
first_column <- data[[0]]
相关文章:

R语言进行正态分布检验
查了很多资料,还是比较模糊 Kolmogorov-Smirnov检验(K-S检验)广泛用于正态性检验和其他分布的拟合检验。适用于中等到大样本。 Lilliefors检验是K-S检验的一种变体,专门为小样本设计。其通过使用更准确的临界值来提高对小样本的适…...

什么是SPA(Single Page Application)?它的优点和缺点是什么?
聚沙成塔每天进步一点点 ⭐ 专栏简介 前端入门之旅:探索Web开发的奇妙世界 欢迎来到前端入门之旅!感兴趣的可以订阅本专栏哦!这个专栏是为那些对Web开发感兴趣、刚刚踏入前端领域的朋友们量身打造的。无论你是完全的新手还是有一些基础的开发…...

由于找不到xinput1_3.dll,无法继续执行代码的多种解决方法指南,xinput1_3.dll文件修复
当玩家或用户在启动某些游戏和应用程序时,可能会遭遇到一个系统错误提示:“由于找不到xinput1_3.dll,无法继续执行代码l”。这种情况通常指出系统中DirectX组件存在问题。以下我们将介绍几种常用的解决方法,并提供详细的操作步骤。 一.找不到…...
Vue---Echarts
项目需要用echarts来做数据展示,现记录vue3引入并使用echarts的过程。 1. 使用步骤 安装 ECharts:使用 npm 或 yarn 等包管理工具安装 ECharts。 npm install echarts 在 Vue 组件中引入 ECharts:在需要使用图表的 Vue 组件中,引入…...

uni-app实现返回刷新上一页
方案一 通过监听器实现 page1 uni.$on("refresh", function(data) {if(data.page "page2") {this.reload()} })page2 methods: {handleBack() {uni.$emit("refresh", {page: "page2"})uni.navigateBack()} }方案二 通过页面实例实…...
centos服务器安装docker和Rabbitmq
centos服务器 一 centos安装docker1 安装docker所需要的依赖包2配置yum源3查看仓库中所有的docker版本4安装docker5 设置docker为开机自启6验证docker是否安装成功 二 使用docker安装RabbitMQ拉取RabbitMQ镜像创建并运行容器 一 centos安装docker 1 安装docker所需要的依赖包 …...

【Redis】Redis高级特性和应用(慢查询、Pipeline、事务、Lua)
目录 Redis的慢查询 慢查询配置 慢查询操作命令 慢查询建议 Pipeline 事务 Redis的事务原理 Redis的watch命令 Pipeline和事务的区别 Lua Lua入门 安装Lua Lua基本语法 注释 标示符 关键词 全局变量 Lua中的数据类型 Lua 中的函数 Lua 变量 Lua中的控制语句…...

【pytorch】深度学习入门一:pytorch的安装与配置(Windows版)
请支持原创,认准DannisTang(tangweixuan1995foxmail.com) 文章目录 第〇章 阅读前提示第一章 准备工作第一节 Python下载第二节 Python安装第三节 Python配置第四节 Pycharm下载第五节 Pycharm安装第六节 CUDA的安装 第二章 Anaconda安装与配…...

安装postgresql驱动及python使用pyodbc指定postgresql驱动调用postgresql
注:Python解释器版本(32位/64位)和postgresql驱动版本(32位/64位)需一致。 一、安装postgresql驱动 https://www.postgresql.org/ftp/odbc/versions/msi/ (1)32位: (2)64位: 双击安装。全程默…...
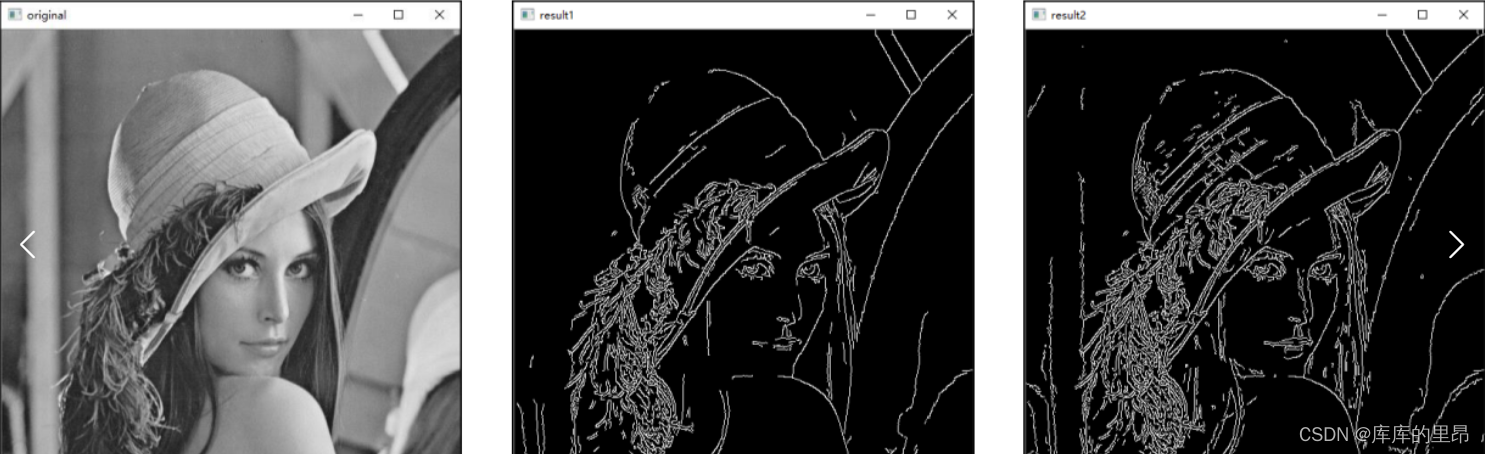
【OpenCV】计算机视觉图像处理基础知识
目录 前言 推荐 1、OpenCV礼帽操作和黑帽操作 2、Sobel算子理论基础及实际操作 3、Scharr算子简介及相关操作 4、Sobel算子和Scharr算子的比较 5、laplacian算子简介及相关操作 6、Canny边缘检测的原理 6.1 去噪 6.2 梯度运算 6.3 非极大值抑制 6.4 滞后阈值 7、Ca…...
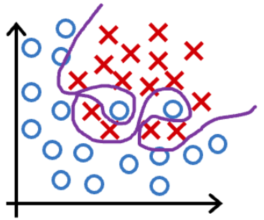
Course1-Week3-分类问题
Course1-Week3-分类问题 文章目录 Course1-Week3-分类问题1. 逻辑回归1.1 线性回归不适用于分类问题1.2 逻辑回归模型1.3 决策边界 2. 逻辑回归的代价函数3. 实现梯度下降4. 过拟合与正则化4.1 线性回归和逻辑回归中的过拟合4.2 解决过拟合的三种方法4.3 正则化4.4 用于线性回归…...
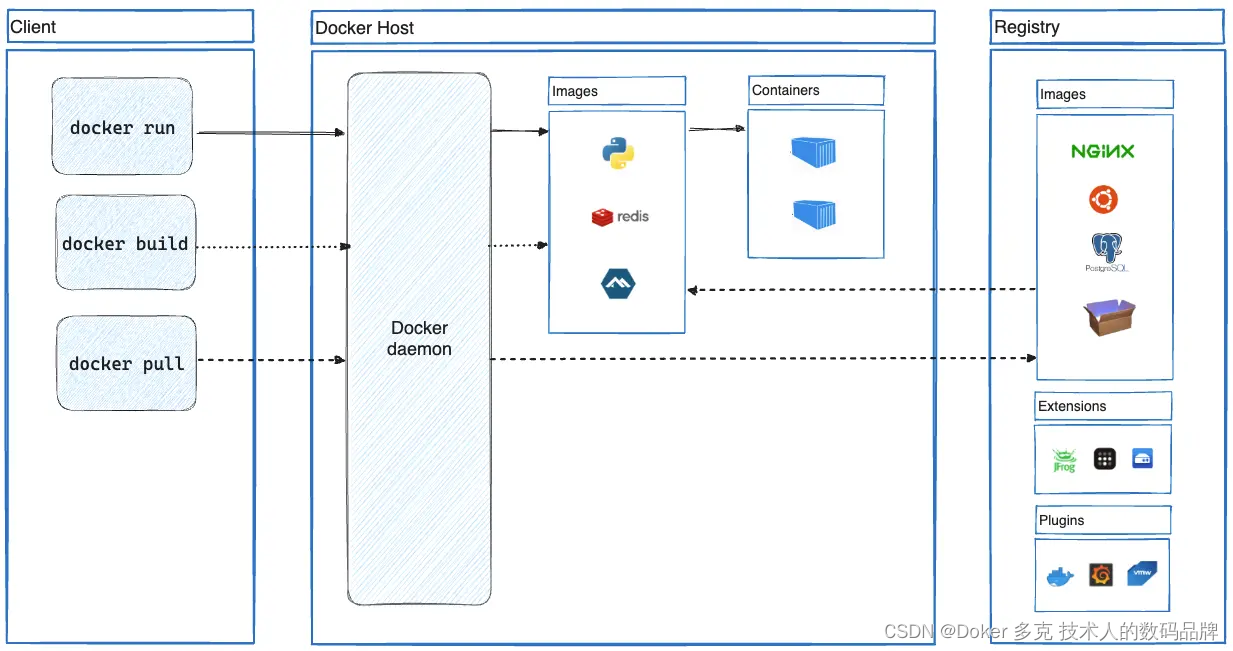
Dockerfile 指令的最佳实践
这些建议旨在帮助您创建一个高效且可维护的Dockerfile。 一、FROM 尽可能使用当前的官方镜像作为镜像的基础。Docker推荐Alpine镜像,因为它受到严格控制,体积小(目前不到6 MB),同时仍然是一个完整的Linux发行版。 FR…...
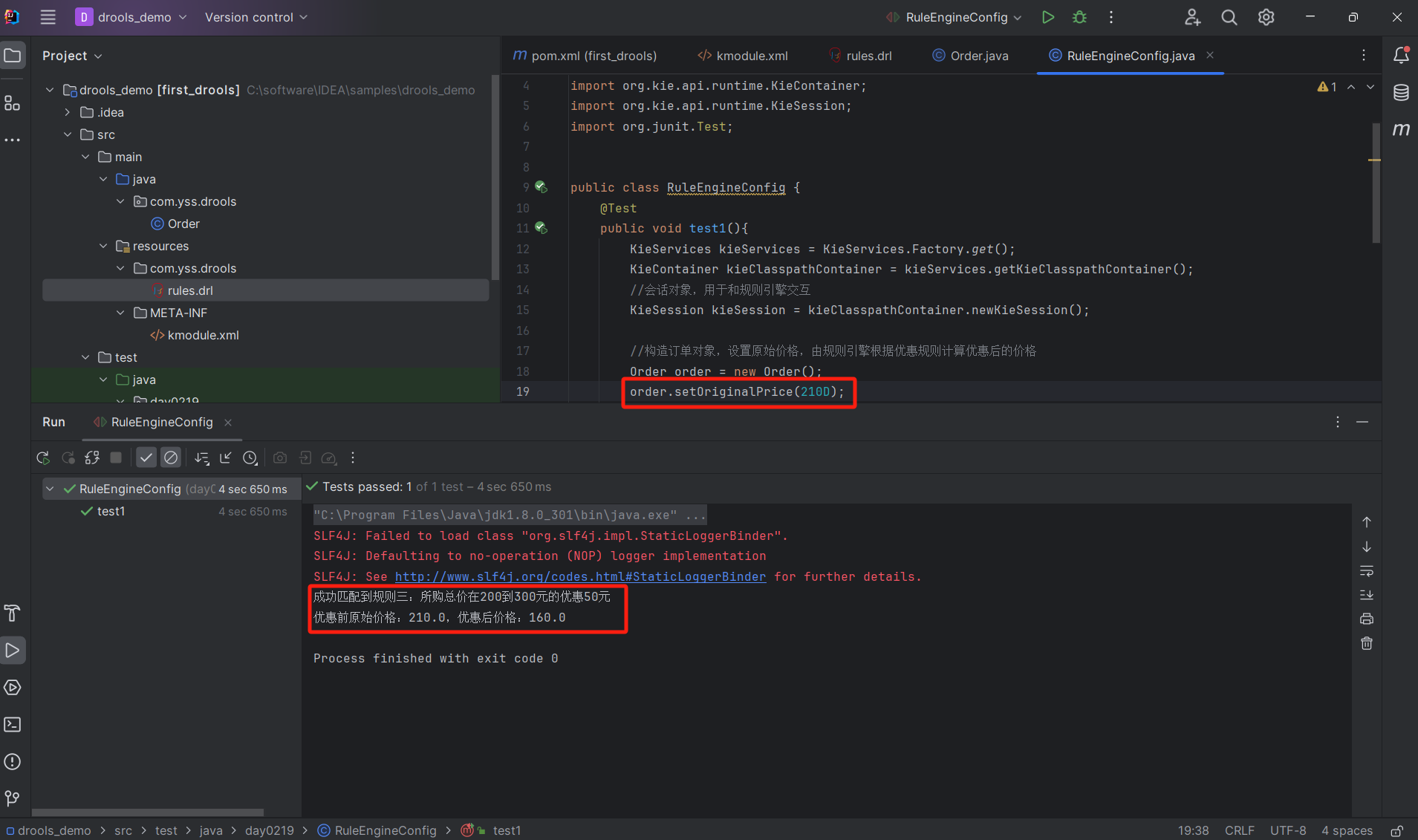
Drools 入门:折扣案例
1. 安装 在idea软件中安装Drools 插件,我这里是直接搜索Drools就可以搜到 2. 实现入门案例 2.1 配置pom.xml文件 <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0"xmlns:xsi&q…...
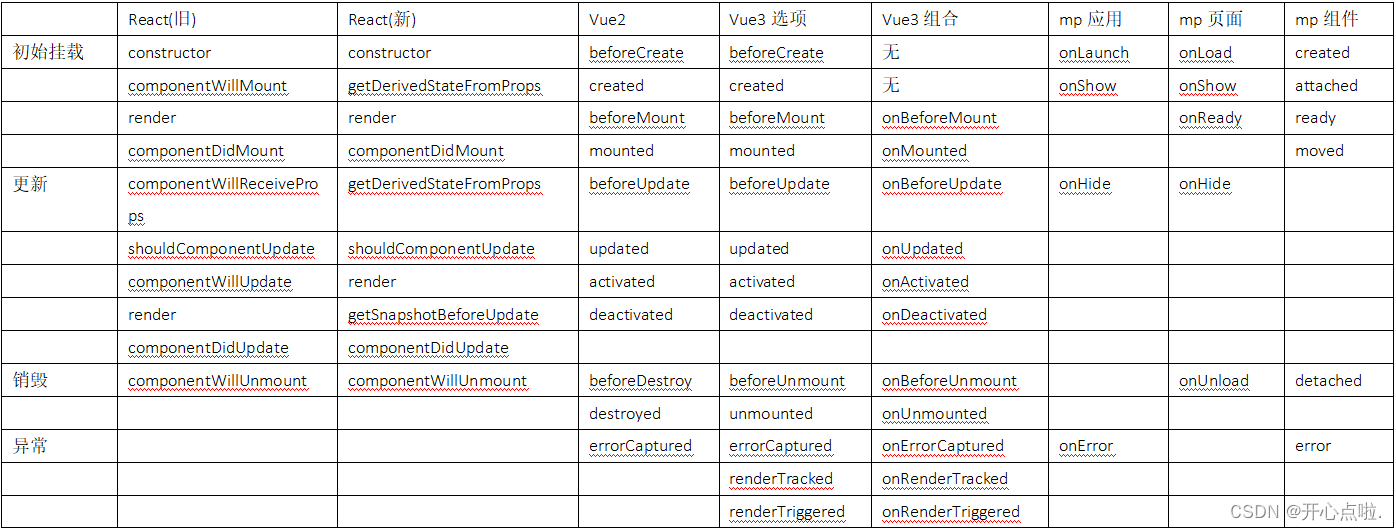
微信小程序中生命周期钩子函数
微信小程序 App 的生命周期钩子函数有以下 7 个: onLaunch(options):当小程序初始化完成时,会触发 onLaunch(全局只触发一次)。onShow(options):当小程序启动或从后台进入前台显示时,会触发 on…...

“无忧文件安全!上海迅软DSE文件加密软件助您轻松管控分公司数据!
许多大型企业集团由于旗下有着分布在不同城市的分支机构,因此在规划数据安全解决方案时,不适合采用市面上常见的集中式部署方式来管控各分部服务器,而迅软DSE文件加密软件支持采用分布式部署的方式来解决这一问题。 企业用户只需在总部内部署…...
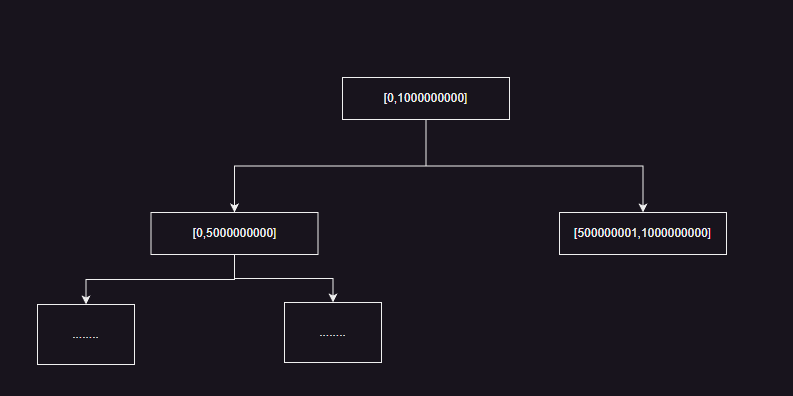
详解线段树
前段时间写过一篇关于树状数组的博客树状数组,今天我们要介绍的是线段树,线段树比树状数组中的应用场景更加的广泛。这些问题也是在leetcode 11月的每日一题频繁遇到的问题,实际上线段树就和红黑树 、堆一样是一类模板,但是标准库…...

C语言——指针的运算
1、指针 - 整数 #include<stdio.h> #define N_VALUES 5 int main() {flout values[N_VALUES];flout *vp;for(vp&values[0];vp<&values[N_VALUES];) //指针的关系运算{*vp0; //指针整数} } 2、指针 - 指针 #include<stdio.h> int main() …...
Apache Hive(部署+SQL+FineBI构建展示)
Hive架构 Hive部署 VMware虚拟机部署 一、在node1节点安装mysql数据库 二、配置Hadoop 三、下载 解压Hive 四、提供mysql Driver驱动 五、配置Hive 六、初始化元数据库 七、启动Hive(Hadoop用户) chown -R hadoop:hadoop apache-hive-3.1.3-bin hive 阿里云部…...

python入门级简易教程
Python是一种高级编程语言,由Guido van Rossum于1991年创建。它是一种通用的、解释型的、高级的、动态的、面向对象的编程语言。 Python的编程哲学是简洁明了,强调代码的可读性和简洁性,使开发人员能够快速开发出正确的代码。Python被广泛用…...

模拟一个集合 里面是设备号和每日的日期
问题: 需要模拟一个集合 里面是设备号和每日的日期 代码如下: static void Main(string[] args){string equipmentCodePar "";DateTime time DateTime.Now; // 获取当前时间DateTime startDate time.AddDays(1 - time.Day);//获取当前月第一…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...
