当前位置： 首页 > news >正文

区块链实验室(28) - 拜占庭节点劫持区块链仿真

news 2026/2/7 13:40:40

在以前的FISCO环境中仿真拜占庭节点攻击区块链网络。该环境共有100个节点，采用PBFT作为共识机制，节点编号分别为：Node0，Node，… ，Node99。这100个节点的前2010区块完全相同，自区块2011开始分叉。

(1)1个拜占庭节点:Node0

Node0 区块长度2020，Node1 - Node99区块长度2030。

在Node0上发起交易，Node0区块同步失败。

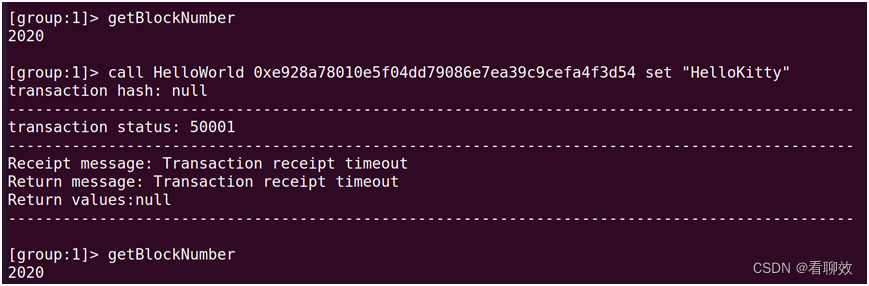
在这里插入图片描述

在其他节点上交易成功，区块同步成功。

在这里插入图片描述

这说明：100个节点中Node0被抛弃，99个节点仍能PBFT共识成功。

反过来，在Node99节点上发起同样的交易，成功。

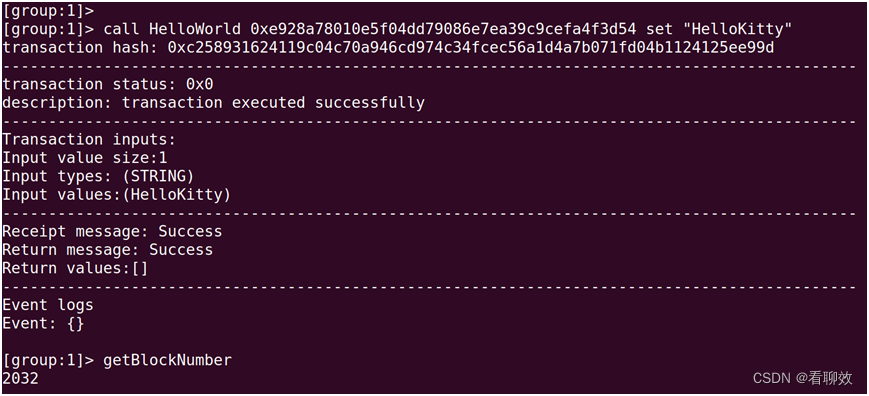
在这里插入图片描述

但Node0节点的区块未更新，节点被抛弃。

在这里插入图片描述

(2)33个拜占庭节点:Node0 – Node32

Node0 – Node32 区块长度2020，Node33 - Node99区块长度2030

在Node0上发起交易，交易失败，区块长度未变。

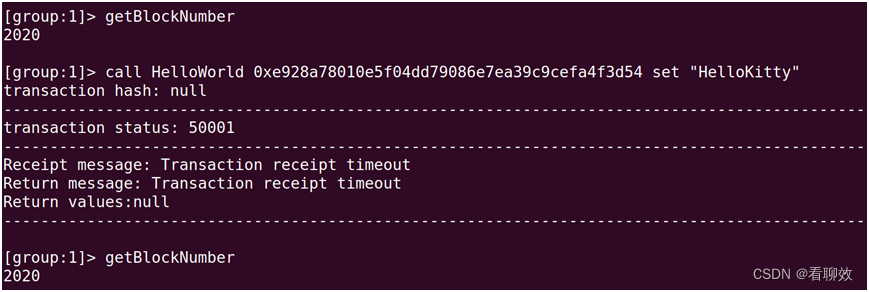
在这里插入图片描述

Node99节点的区块长度也未变，说明交易失败。

在这里插入图片描述

反过来，在Node99节点上发起同样的交易，同样失败。

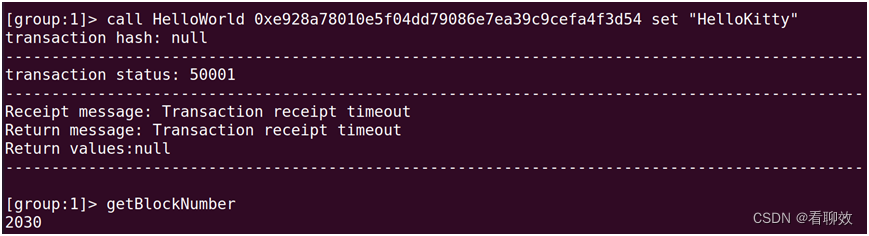
在这里插入图片描述

Node0节点的区块长度也未变，交易彻底失败。

在这里插入图片描述

此时，整个区块链失去共识能力。

(3)32个拜占庭节点:Node0 – Node31

Node0 – Node31 区块长度2020，Node32 - Node99区块长度2030

在Node0上发起交易，Node0的区块长度未变。

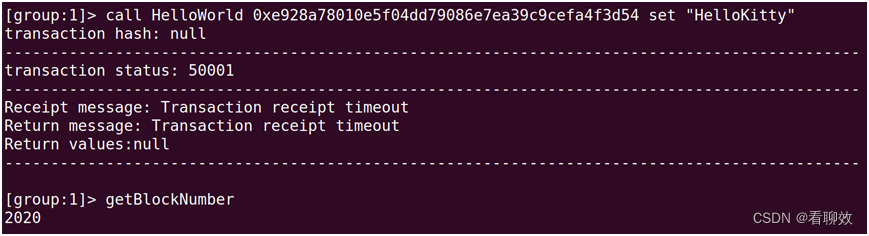
在这里插入图片描述

但在Node99上区块长度加1，说明交易成功。

在这里插入图片描述

相同地，在Node99上发起交易，交易成功，区块长度加1.

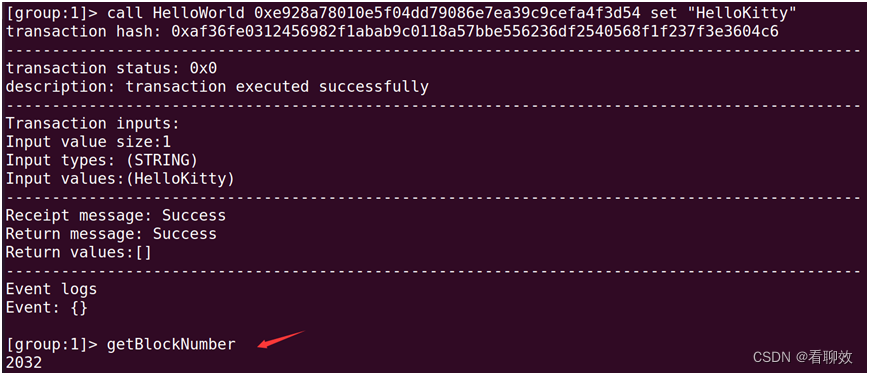
在这里插入图片描述

然而，Node0节点的区块长度未变。

在这里插入图片描述

此时，整个区块链还具有共识能力。结论：在FISCO环境中，PBFT共识的条件是N>3f+1，其中N是节点总数，f是拜占庭节点数量。

相关文章：

区块链实验室(28) - 拜占庭节点劫持区块链仿真

在以前的FISCO环境中仿真拜占庭节点攻击区块链网络。该环境共有100个节点，采用PBFT作为共识机制，节点编号分别为：Node0，Node，… ，Node99。这100个节点的前2010区块完全相同，自区块2011开始分叉。…...

编程日记 2023/12/8 17:26:42

聊聊AsyncHttpClient的ChannelPool

序 本文主要研究一下AsyncHttpClient的ChannelPool ChannelPool org/asynchttpclient/channel/ChannelPool.java public interface ChannelPool {/*** Add a channel to the pool** param channel an I/O channel* param partitionKey a key used to retrieve the cac…...

编程日记 2023/12/8 17:22:38

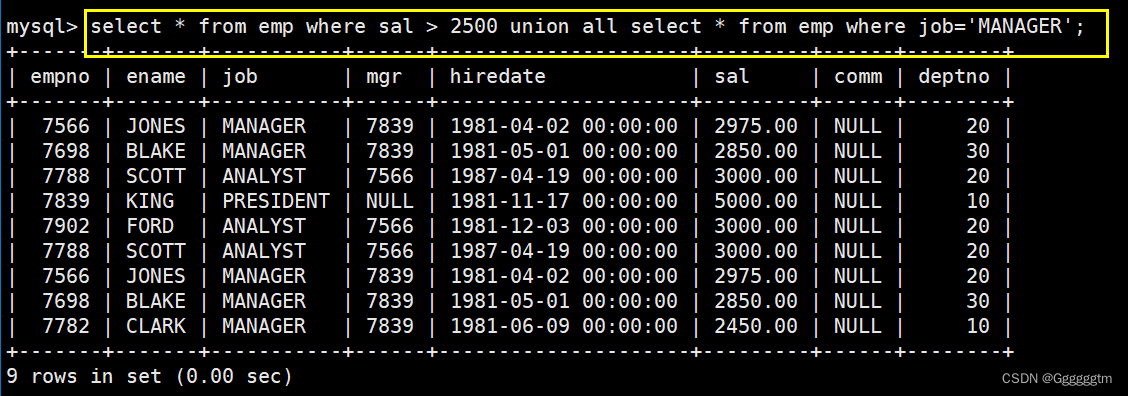
[MySQL] MySQL复合查询（多表查询、子查询）

前面我们学习了MySQL简单的单表查询。但是我们发现，在很多情况下单表查询并不能很好的满足我们的查询需求。本篇文章会重点讲解MySQL中的多表查询、子查询和一些复杂查询。希望本篇文章会对你有所帮助。 文章目录 一、基本查询回顾 二、多表查询 2、1 笛卡尔积 2、2…...

编程日记 2023/12/8 17:19:35

[架构之路-256]：目标系统 - 设计方法 - 软件工程 - 软件设计 - 架构设计 - 软件系统不同层次的复用与软件系统向越来越复杂的方向聚合

目录 前言： 一、CPU寄存器级的复用：CPU寄存器 二、指令级复用：二进制指令 三、过程级复用：汇编语言 四、函数级复用：C语言 五、对象级复用：C, Java, Python 六、组件级复用 七、服务级复用 八、微…...

编程日记 2023/12/8 17:18:34

C++初学教程三

目录 一、运算符 一、自增自减运算符 二、位运算符 三、关系运算符...

编程日记 2023/12/8 17:17:34

雷达点云数据.pcd格式转.bin格式

雷达点云数据.pcd格式转.bin格式 注意，方法1原则上可行，但是本人没整好pypcd的环境 方法2是绝对可以的。 方法1 1 源码如下： def pcb2bin1(): # save as bin formatimport os# import pypcdfrom pypcd import pypcdimport numpy as np…...

编程日记 2023/12/8 17:16:33

Fiddler抓包测试

模拟弱网测试 操作：一、Rules - Customize Rules （快捷键CtrlR）弹出编辑器 二、接着CtrlF查找m_SimulateModem标志位 三、默认上传300ms，下载150ms 四、更改后，继续Rules - Performances - Simulate Modem Speeds勾上 …...

编程日记 2023/12/8 17:13:30

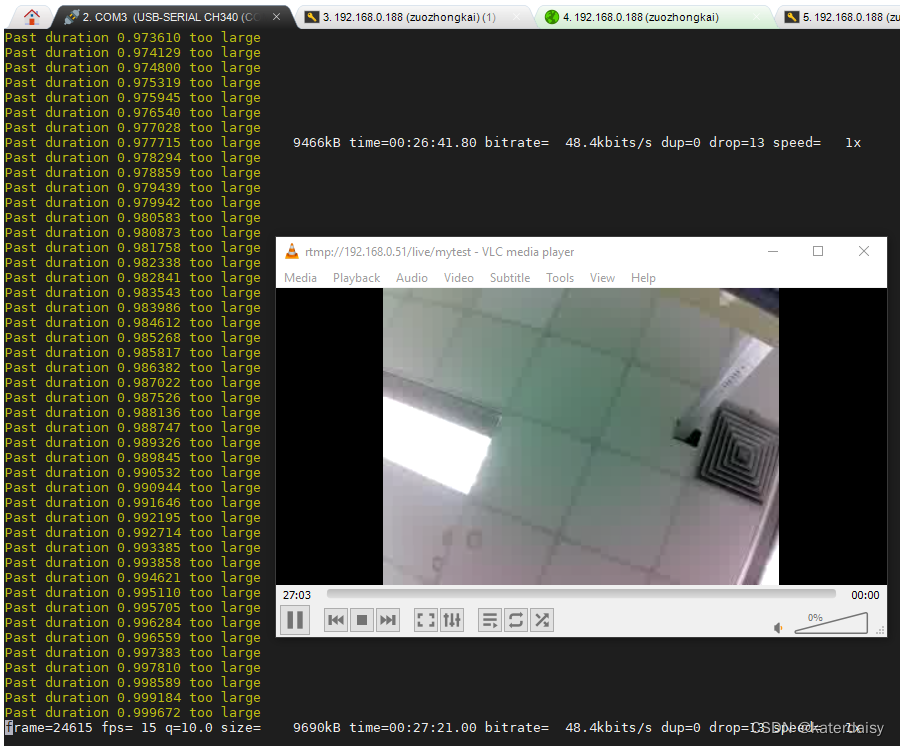
视频处理关键知识

1 引言 视频技术发展到现在已经有100多年的历史，虽然比照相技术历史时间短，但在过去很长一段时间之内都是最重要的媒体。由于互联网在新世纪的崛起，使得传统的媒体技术有了更好的发展平台，应运而生了新的多媒体技术。而多媒体技术…...

编程日记 2023/12/8 17:12:29

LeetCode435. Non-overlapping Intervals

文章目录 一、题目二、题解 一、题目 Given an array of intervals intervals where intervals[i] [starti, endi], return the minimum number of intervals you need to remove to make the rest of the intervals non-overlapping. Example 1: Input: intervals [[1,2]…...

编程日记 2023/12/8 17:10:26

ffmpeg 实现多视频轨录制到同一个文件

引言 在视频录制中，有时会碰到这样一个需求，将不同摄像头的画面写入到一个视频文件，这个叫法很多，有的厂家叫合流模式，有的叫多画面多流模式。无论如何，它们的实质都是在一个视频文件上实现多路不同分辨率视…...

编程日记 2023/12/8 17:09:25

vue3中子组件调用父组件的方法

<script lang"ts" setup>前提 父组件&#xff1a; 子组件&#xff1a; const emit defineEmits([closeson]) 在子组件的方法中使用&#xff1a; emit(closeson)...

编程日记 2023/12/8 17:05:19

使用OkHttp上传本地图片及参数

下面以一个例子来讲解在项目中如何使用OKHttp来对本地图片做个最简单的上传功能&#xff0c;基本上无封装&#xff0c;只需要简单调用便可&#xff08;对于OKHttp的引入不再单独做介绍&#xff09;。 1&#xff1a;构建上传图片附带的参数&#xff08;params&#xff09; Map…...

编程日记 2023/12/8 17:04:18

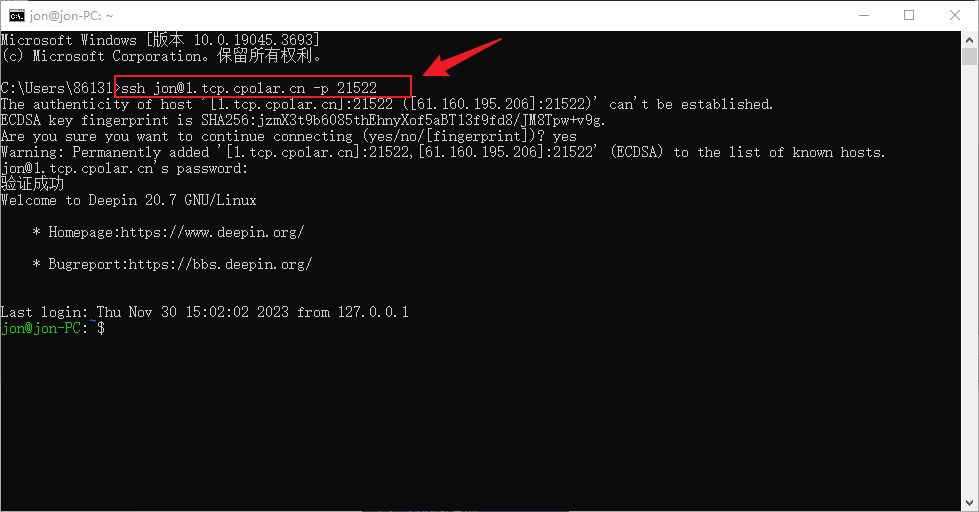
无公网IP环境如何SSH远程连接Deepin操作系统

文章目录 前言1. 开启SSH服务2. Deppin安装Cpolar3. 配置ssh公网地址4. 公网远程SSH连接5. 固定连接SSH公网地址6. SSH固定地址连接测试 前言 Deepin操作系统是一个基于Debian的Linux操作系统&#xff0c;专注于使用者对日常办公、学习、生活和娱乐的操作体验的极致&#xff0…...

编程日记 2023/12/8 17:03:17

不会代码（零基础）学语音开发（语音控制板载双继电器）

继电器的用途可广了&#xff0c;这个语音控制用处也特别广。继电器&#xff0c;它实际上是一种“自动开关”&#xff0c;用小电流去控制大电流运作&#xff0c;在电路中起着自动调节、安全保护、转换电路等作用。 在日常生活中&#xff0c;你插入汽车钥匙&#xff0c;车辆可以…...

编程日记 2023/12/8 17:01:15

在imx6ull中加入ov5640模块

本来觉得是一件很简单的事情但是走了很多的弯路&#xff0c;记录一下调试过程。 先使用正点原子提供的出厂内核把摄像头影像调试出来&#xff0c;然后cat /dev/video1&#xff0c;看一下video1牵扯到哪些模块&#xff0c;可以看到需要ov5640_camera.ko和 mx6s_capture.ko这两个…...

编程日记 2023/12/8 17:00:13

Kafka中的auto-offset-reset配置

Kafka这个服务在启动时会依赖于Zookeeper&#xff0c;Kafka相关的部分数据也会存储在Zookeeper中。如果kafka或者Zookeeper中存在脏数据的话&#xff08;即错误数据&#xff09;&#xff0c;这个时候虽然生产者可以正常生产消息&#xff0c;但是消费者会出现无法正常消费消息的…...

编程日记 2023/12/8 16:59:12

TCP/IP_整理起因

先分享一个初级的问题&#xff1b;有个客户现场&#xff0c;终端设备使用客户网络更新很慢&#xff0c;使用手机热点更新速度符合预期&#xff1b;网络部署情况如下&#xff1a; 前期花费了很大的精力进行问题排查对比&#xff0c;怀疑是客户网络问题&#xff08;其他的客户现…...

编程日记 2023/12/8 16:57:11

CG-0A 电子水尺水导电测量原理应用于道路积水监测

CG-0A 电子水尺水导电测量原理应用于道路积水监测产品概述 本产品是一种采用微处理器芯片为控制器&#xff0c;内置通讯电路的数字式水位传感器&#xff0c;具备高的可靠性及抗干扰性能。适用于江、河、湖、水库及蓄水池、水渠等处的水位测量使用。 本产品采用了生产工艺技术…...

编程日记 2023/12/8 16:56:09

openEuler JDK21 部署 Zookeeper 集群

zookeeper-jdk21 操作系统&#xff1a;openEuler JDK&#xff1a;21 主机名IP地址spark01192.168.171.101spark02192.168.171.102spark03192.168.171.103 安装 1. 升级内核和软件 yum -y update2. 安装常用软件 yum -y install gcc gcc-c autoconf automake cmake make \zl…...

编程日记 2023/12/8 16:52:06

前端——html拖拽原理

文章目录 ⭐前言⭐draggable属性&#x1f496; api&#x1f496; 单向拖动示例&#x1f496; 双向拖动示例 ⭐总结⭐结束 ⭐前言 大家好&#xff0c;我是yma16&#xff0c;本文分享关于 前端——html拖拽原理。 vue3系列相关文章&#xff1a; vue3 fastapi 实现选择目录所有文…...

编程日记 2023/12/8 16:48:02

vscode里如何用git

打开vs终端执行如下&#xff1a; 1 初始化 Git 仓库&#xff08;如果尚未初始化&#xff09; git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

编程新知 2025/8/24 20:45:38

椭圆曲线密码学(ECC)

一、ECC算法概述 椭圆曲线密码学&#xff08;Elliptic Curve Cryptography&#xff09;是基于椭圆曲线数学理论的公钥密码系统&#xff0c;由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA&#xff0c;ECC在相同安全强度下密钥更短&#xff08;256位ECC ≈ 3072位RSA…...

编程新知 2025/10/1 22:26:06

浅谈不同二分算法的查找情况

二分算法原理比较简单&#xff0c;但是实际的算法模板却有很多&#xff0c;这一切都源于二分查找问题中的复杂情况和二分算法的边界处理&#xff0c;以下是博主对一些二分算法查找的情况分析。 需要说明的是&#xff0c;以下二分算法都是基于有序序列为升序有序的情况&#xf…...

编程新知 2025/9/14 7:37:32

【Linux】Linux 系统默认的目录及作用说明

博主介绍&#xff1a;✌全网粉丝23W&#xff0c;CSDN博客专家、Java领域优质创作者&#xff0c;掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围&#xff1a;SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...

编程新知 2026/1/29 2:30:31

jmeter聚合报告中参数详解

sample、average、min、max、90%line、95%line,99%line、Error错误率、吞吐量Thoughput、KB/sec每秒传输的数据量 sample&#xff08;样本数&#xff09; 表示测试中发送的请求数量&#xff0c;即测试执行了多少次请求。 单位&#xff0c;以个或者次数表示。 示例&#xff1a;…...

编程新知 2025/12/18 6:00:45

Chromium 136 编译指南 Windows篇：depot_tools 配置与源码获取（二）

引言 工欲善其事&#xff0c;必先利其器。在完成了 Visual Studio 2022 和 Windows SDK 的安装后&#xff0c;我们即将接触到 Chromium 开发生态中最核心的工具——depot_tools。这个由 Google 精心打造的工具集&#xff0c;就像是连接开发者与 Chromium 庞大代码库的智能桥梁…...

编程新知 2026/1/25 20:54:41

「全栈技术解析」推客小程序系统开发：从架构设计到裂变增长的完整解决方案

在移动互联网营销竞争白热化的当下&#xff0c;推客小程序系统凭借其裂变传播、精准营销等特性&#xff0c;成为企业抢占市场的利器。本文将深度解析推客小程序系统开发的核心技术与实现路径&#xff0c;助力开发者打造具有市场竞争力的营销工具。​ 一、系统核心功能架构&…...

编程新知 2025/8/21 16:28:18

Python 高效图像帧提取与视频编码：实战指南

Python 高效图像帧提取与视频编码：实战指南 在音视频处理领域，图像帧提取与视频编码是基础但极具挑战性的任务。Python 结合强大的第三方库（如 OpenCV、FFmpeg、PyAV），可以高效处理视频流，实现快速帧提取、压缩编码等关键功能。本文将深入介绍如何优化这些流程，提高处理…...

编程新知 2025/8/31 18:02:53

论文阅读：Matting by Generation

今天介绍一篇关于 matting 抠图的文章&#xff0c;抠图也算是计算机视觉里面非常经典的一个任务了。从早期的经典算法到如今的深度学习算法&#xff0c;已经有很多的工作和这个任务相关。这两年 diffusion 模型很火&#xff0c;大家又开始用 diffusion 模型做各种 CV 任务了&am…...

编程新知 2026/1/27 19:36:39

机器学习的数学基础：线性模型

线性模型 线性模型的基本形式为&#xff1a; f ( x ) ω T x b f\left(\boldsymbol{x}\right)\boldsymbol{\omega}^\text{T}\boldsymbol{x}b f(x)ωTxb 回归问题 利用最小二乘法&#xff0c;得到 ω \boldsymbol{\omega} ω和 b b b的参数估计$ \boldsymbol{\hat{\omega}}…...

编程新知 2025/10/2 9:07:50