B. The Number of Products)厉害
You are given a sequence a1,a2,…,ana1,a2,…,an consisting of nn non-zero integers (i.e. ai≠0ai≠0).
You have to calculate two following values:
- the number of pairs of indices (l,r)(l,r) (l≤r)(l≤r) such that al⋅al+1…ar−1⋅aral⋅al+1…ar−1⋅ar is negative;
- the number of pairs of indices (l,r)(l,r) (l≤r)(l≤r) such that al⋅al+1…ar−1⋅aral⋅al+1…ar−1⋅ar is positive;
Input
The first line contains one integer nn (1≤n≤2⋅105)(1≤n≤2⋅105) — the number of elements in the sequence.
The second line contains nn integers a1,a2,…,ana1,a2,…,an (−109≤ai≤109;ai≠0)(−109≤ai≤109;ai≠0) — the elements of the sequence.
Output
Print two integers — the number of subsegments with negative product and the number of subsegments with positive product, respectively.
Examples
input
Copy
5 5 -3 3 -1 1
output
Copy
8 7
input
Copy
10 4 2 -4 3 1 2 -4 3 2 3
output
Copy
28 27
input
Copy
5 -1 -2 -3 -4 -5
output
Copy
9 6
给你一个由n个非零整数(即ai≠0)组成的序列a1,a2,...,an。
你必须计算以下两个值。
指数(l,r)的数目(l≤r),使al⋅al+1...ar-1⋅ar为负数。
使得al⋅al+1...ar-1⋅ar为正数的一对索引(l,r)(l≤r)的数量。
输入
第一行包含一个整数n(1≤n≤2⋅105)--序列中的元素数。
第二行包含n个整数a1,a2,...,an (-109≤ai≤109;ai≠0) - 序列的元素。
输出
打印两个整数 - 负积的子段数和正积的子段数,分别为。
意思:
题目意思是说输出负积子段数和正积子段数。既然都是积,那么只要出现负数就可能改变积的正负,也就是说在遍历的时候要考虑出现负数的情况,如果只存在正数,那么直接1+2+3+。。。+n就能得到答案。
如果出现负数那么就交换正负数的计数,然后在负数奇数上面+1;
#include<iostream>
#include<cmath>
#include<cstring>
#include<cstdio>
#include<stack>
#include<string>
#include<algorithm>
#include<unordered_map>
#include<map>
#include<cstring>
#include<queue>
#include<set>
#include<stdlib.h>
#define dbug cout<<"hear!"<<endl;
#define rep(a,b) for(int i=a;i<=b;i++)
#define rrep(a,b) for(int j=a;j<=b;j++)
#define per(a,b) for(int i=a;i>=b;i--)
#define pper(a,b) for(int j=a;j>=b;j--)
#define no cout<<"NO"<<endl;
#define yes cout<<"YES"<<endl;
using namespace std;
typedef long long ll;
typedef long double ld;
const int N = 2e5 + 100;
const int INF = 0x3f3f3f3f;
ll gcdd(ll a, ll b)
{if (b) while ((a %= b) && (b %= a));return a + b;
}
const int mod = 998244353;
ll t, n, m, a, b, c, x, k, cnt, ans, ant, sum, q, p, idx;
ll arr[N], brr[N], crr[N];
ll axx[2000][2000];
bool book[N];
char s[N];int main()
{cin >> n;ant = 0;cnt = 0;ans = 0;ll zheng = 0, fu = 0;rep(1, n){cin >> x;if (x > 0){ant++;}else{swap(ant, cnt);cnt++;}zheng += ant;fu += cnt;}cout << fu << ' ' << zheng;
}
相关文章:
厉害)
B. The Number of Products)厉害
You are given a sequence a1,a2,…,ana1,a2,…,an consisting of nn non-zero integers (i.e. ai≠0ai≠0). You have to calculate two following values: the number of pairs of indices (l,r)(l,r) (l≤r)(l≤r) such that al⋅al1…ar−1⋅aral⋅al1…ar−1⋅ar is neg…...
)
一起Talk Android吧(第五百一十二回:自定义Dialog)
文章目录整体思路实现方法第一步第二步第三步第四步各位看官们大家好,上一回中咱们说的例子是"自定义Dialog主题",这一回中咱们说的例子是" 自定义Dialog"。闲话休提,言归正转, 让我们一起Talk Android吧!整体…...
GinVueAdmin源码分析3-整合MySQL
目录文件结构数据库准备配置文件处理config.godb_list.gogorm_mysql.gosystem.go初始化数据库gorm.gogorm_mysql.go开始初始化测试数据库定义实体类 Userserviceapi开始测试!文件结构 本文章将使用到上一节创建的 CommonService 接口,用于测试连接数据库…...
MapReduce框架原理——MapReduce开发总结)
大数据框架之Hadoop:MapReduce(三)MapReduce框架原理——MapReduce开发总结
在编写MapReduce程序时,需要考虑如下几个方面: 1、输入数据接口:InputFormat 默认使用的实现类是:TextInputFormatTextInputFormat的功能逻辑是:一次读一行文本,然后将该行的起始偏移量作为key࿰…...

requests---(4)发送post请求完成登录
前段时间写过一个通过cookies完成登录,今天我们写一篇通过post发送请求完成登录豆瓣网 模拟登录 1、首先找到豆瓣网的登录接口 打开豆瓣网站的登录接口,请求错误的账号密码,通过F12或者抓包工具找到登录接口 通过F12抓包获取到请求登录接口…...
Python抓取数据具体流程
之前看了一段有关爬虫的网课深有启发,于是自己也尝试着如如何过去爬虫百科“python”词条等相关页面的整个过程记录下来,方便后期其他人一起来学习。 抓取策略 确定目标:重要的是先确定需要抓取的网站具体的那些部分,下面实例是…...
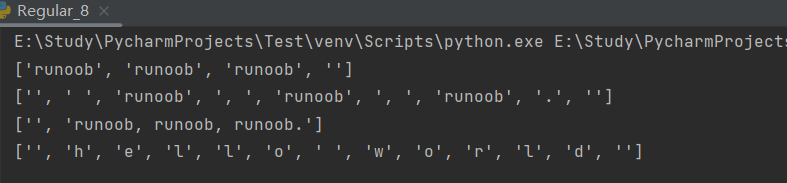
【Python学习笔记】第二十四节 Python 正则表达式
一、正则表达式简介正则表达式(regular expression)是一个特殊的字符序列,它能帮助你方便的检查一个字符串是否与某种模式匹配。正则表达式是对字符串(包括普通字符(例如,a 到 z 之间的字母)和特…...
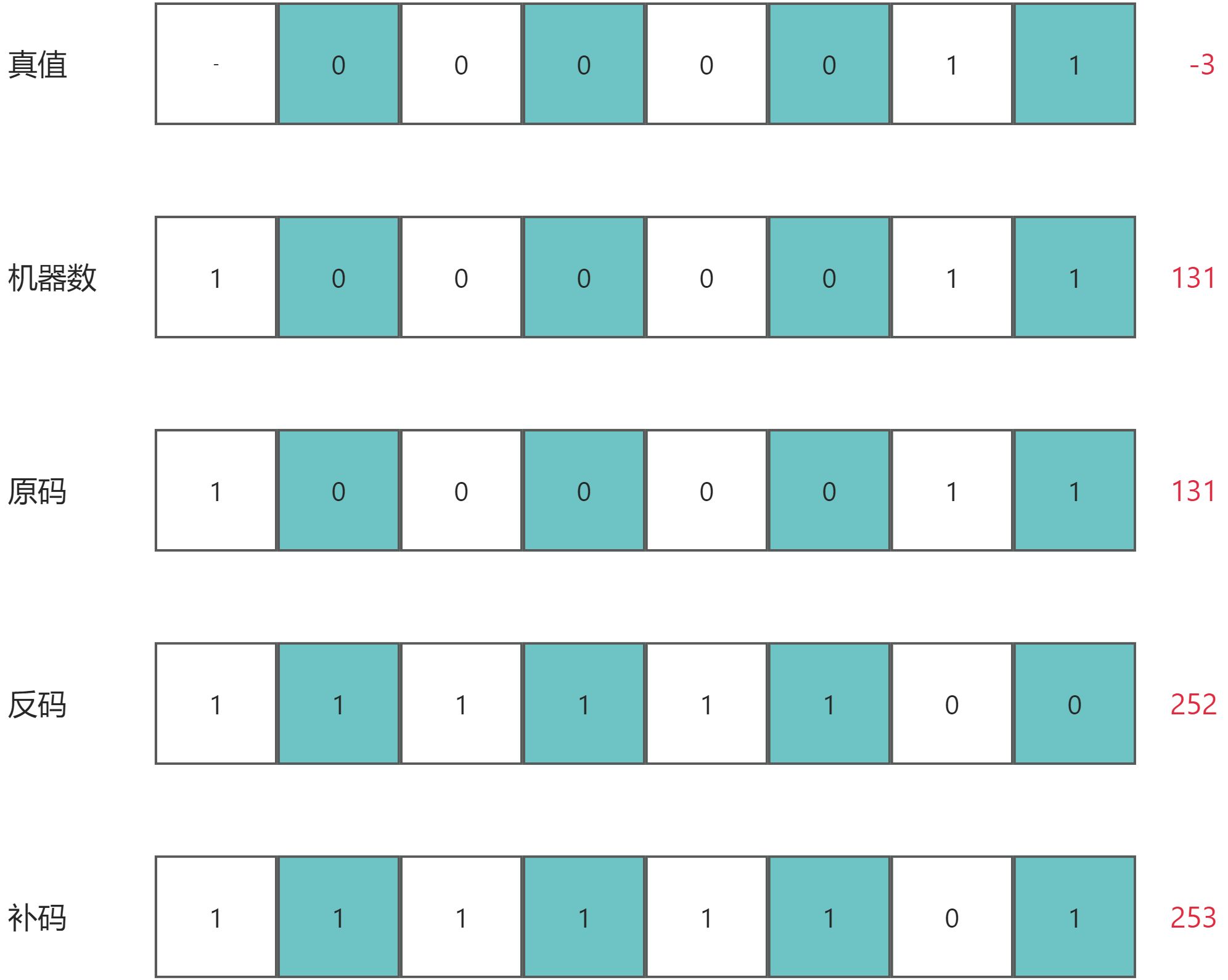
数字逻辑基础:原码、反码、补码
时间紧、不理解可以只看这里的结论 正数的原码、反码、补码相同。等于真值对应的机器码。 负数的原码等于机器码,反码为原码的符号位不变,其余各位按位取反。补码为反码1。 三种码的出现是为了解决计算问题并简化电路结构。 在原码和反码中,存…...

有限差分法-差商公式及其Matlab实现
2.1 有限差分法 有限差分法 (finite difference method)是一种数值求解偏微分方程的方法,它将偏微分方程中的连续变量离散化为有限个点上的函数值,然后利用差分逼近导数,从而得到一个差分方程组。通过求解差分方程组,可以得到原偏微分方程的数值解。 有限差分法是一种历史…...

高校就业信息管理系统
1引言 1.1编写目的 1.2背景 1.3定义 1.4参考资料 2程序系统的结构 3登录模块设计说明一 3.1程序描述 3.2功能 3.3性能 3.4输人项 3.5输出项 3.6算法 3.7流程逻辑 3.8接口 3.10注释设计 3.11限制条件 3.12测试计划 3.13尚未解决的问题 4注册模块设计说明 4.…...

【Java|golang】2373. 矩阵中的局部最大值
给你一个大小为 n x n 的整数矩阵 grid 。 生成一个大小为 (n - 2) x (n - 2) 的整数矩阵 maxLocal ,并满足: maxLocal[i][j] 等于 grid 中以 i 1 行和 j 1 列为中心的 3 x 3 矩阵中的 最大值 。 换句话说,我们希望找出 grid 中每个 3 x …...
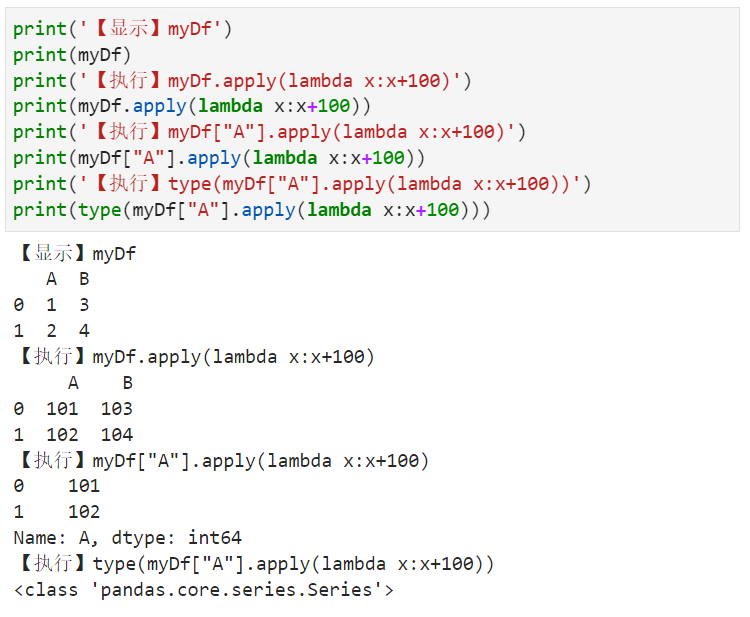
根据指定函数对DataFrame中各元素进行计算
【小白从小学Python、C、Java】【计算机等级考试500强双证书】【Python-数据分析】根据指定函数对DataFrame中各元素进行计算以下错误的一项是?import numpy as npimport pandas as pdmyDict{A:[1,2],B:[3,4]}myDfpd.DataFrame(myDict)print(【显示】myDf)print(myDf)print(【…...

【蓝桥杯集训·每日一题】AcWing 3502. 不同路径数
文章目录一、题目1、原题链接2、题目描述二、解题报告1、思路分析2、时间复杂度3、代码详解三、知识风暴一、题目 1、原题链接 3502. 不同路径数 2、题目描述 给定一个 nm 的二维矩阵,其中的每个元素都是一个 [1,9] 之间的正整数。 从矩阵中的任意位置出发…...
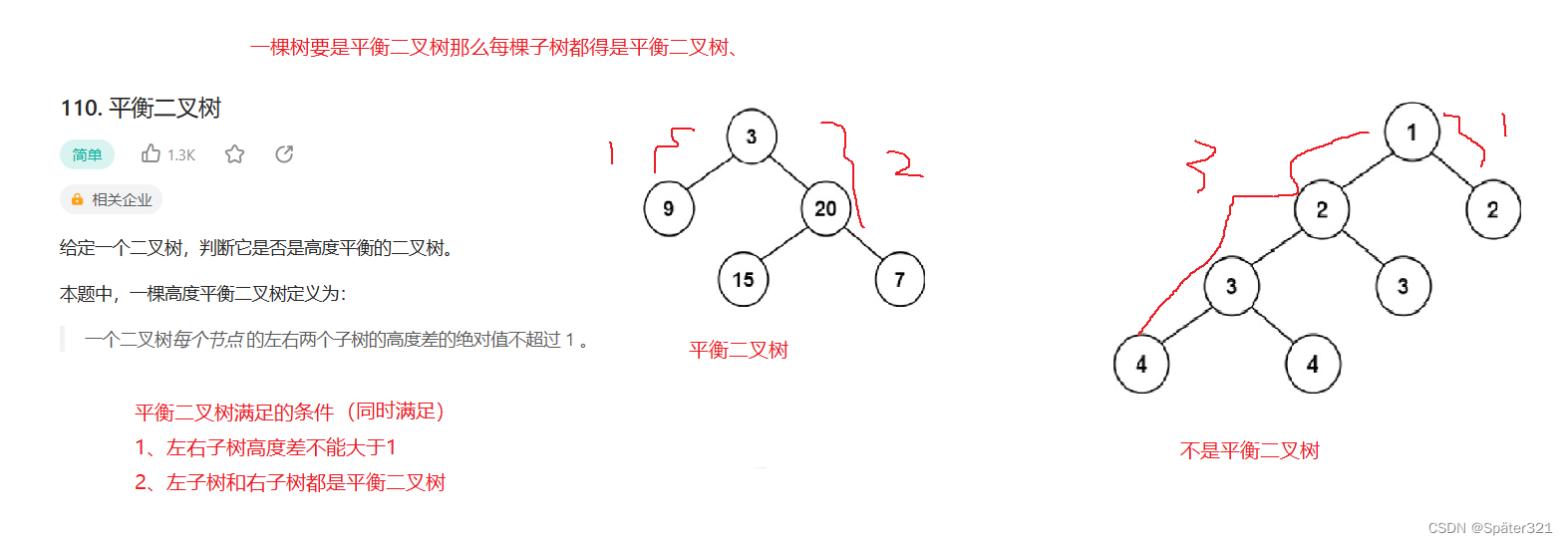
Java - 数据结构,二叉树
一、什么是树 概念 树是一种非线性的数据结构,它是由n(n>0)个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。它具有以下的特点: 1、有…...
模拟QQ登录-课后程序(JAVA基础案例教程-黑马程序员编著-第十一章-课后作业)
【案例11-3】 模拟QQ登录 【案例介绍】 1.案例描述 QQ是现实生活中常用的聊天工具,QQ登录界面看似小巧、简单,但其中涉及的内容却很多,对于初学者练习Java Swing工具的使用非常合适。本案例要求使用所学的Java Swing知识,模拟实…...
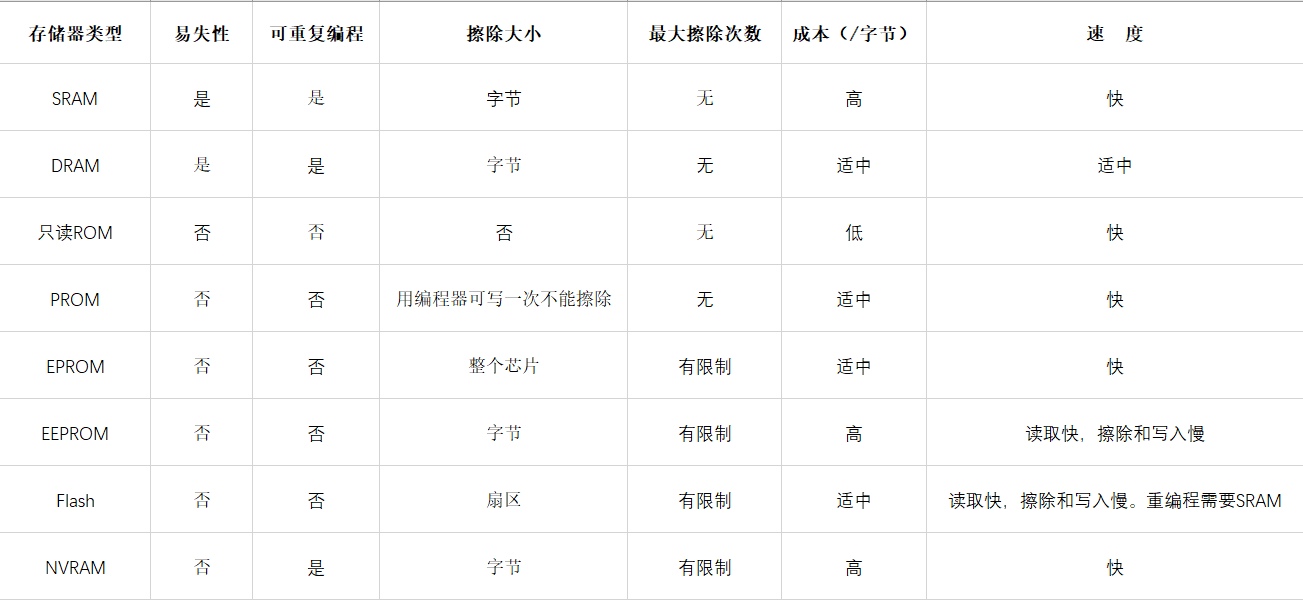
【壹】嵌入式系统硬件基础
随手拍拍💁♂️📷 日期: 2023.2.28 地点: 杭州 介绍: 日子像旋转毒马🐎,在脑海里转不停🤯 🌲🌲🌲🌲🌲 往期回顾 🌲🌲🌲…...
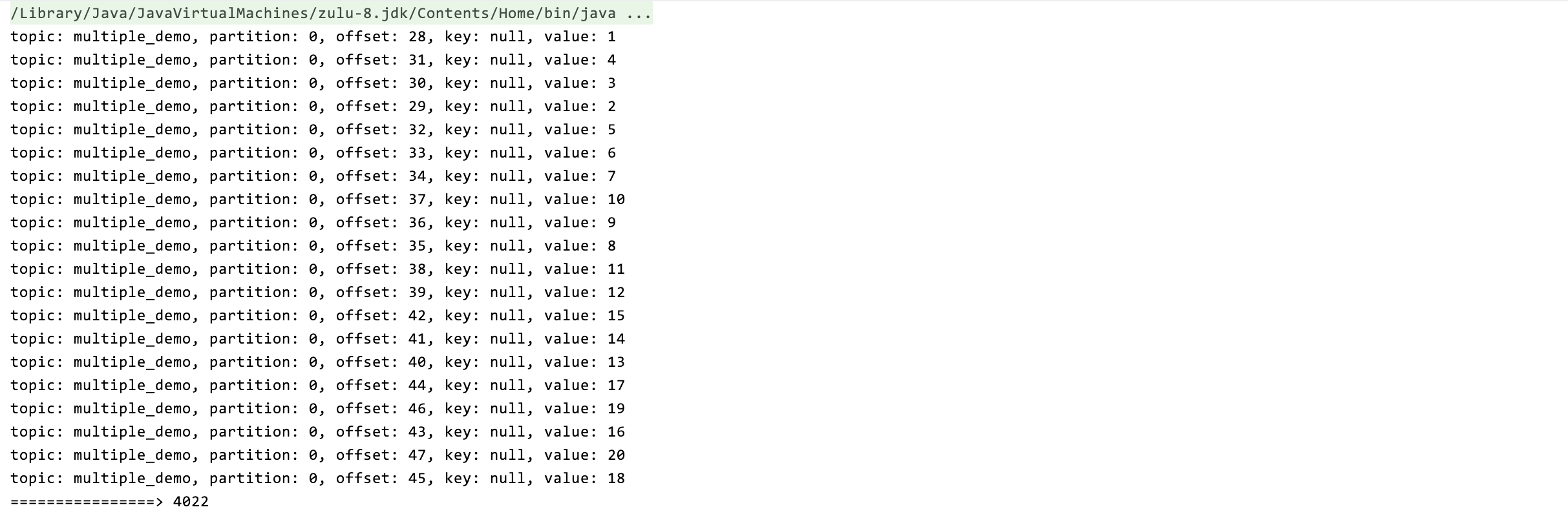
当参数调优无法解决kafka消息积压时可以这么做
今天的议题是:如何快速处理kafka的消息积压 通常的做法有以下几种: 增加消费者数增加 topic 的分区数,从而进一步增加消费者数调整消费者参数,如max.poll.records增加硬件资源 常规手段不是本文的讨论重点或者当上面的手段已经使…...
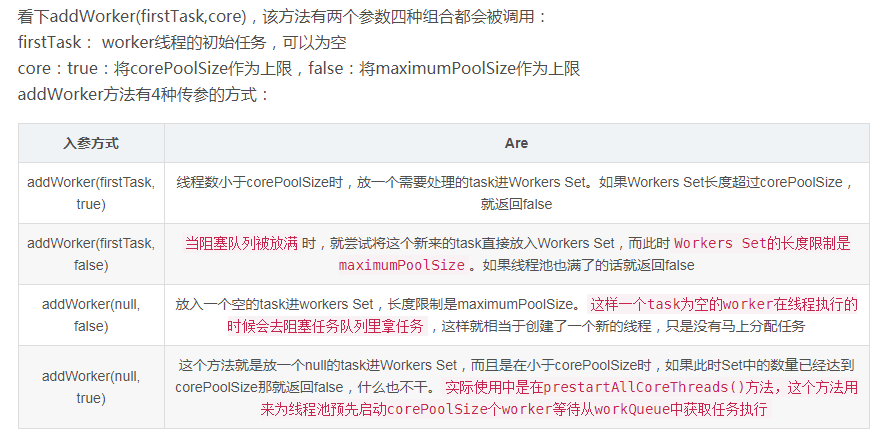
Java线程池源码分析
Java 线程池的使用,是面试必问的。下面我们来从使用到源码整理一下。 1、构造线程池 通过Executors来构造线程池 1、构造一个固定线程数目的线程池,配置的corePoolSize与maximumPoolSize大小相同, 同时使用了一个无界LinkedBlockingQueue存…...
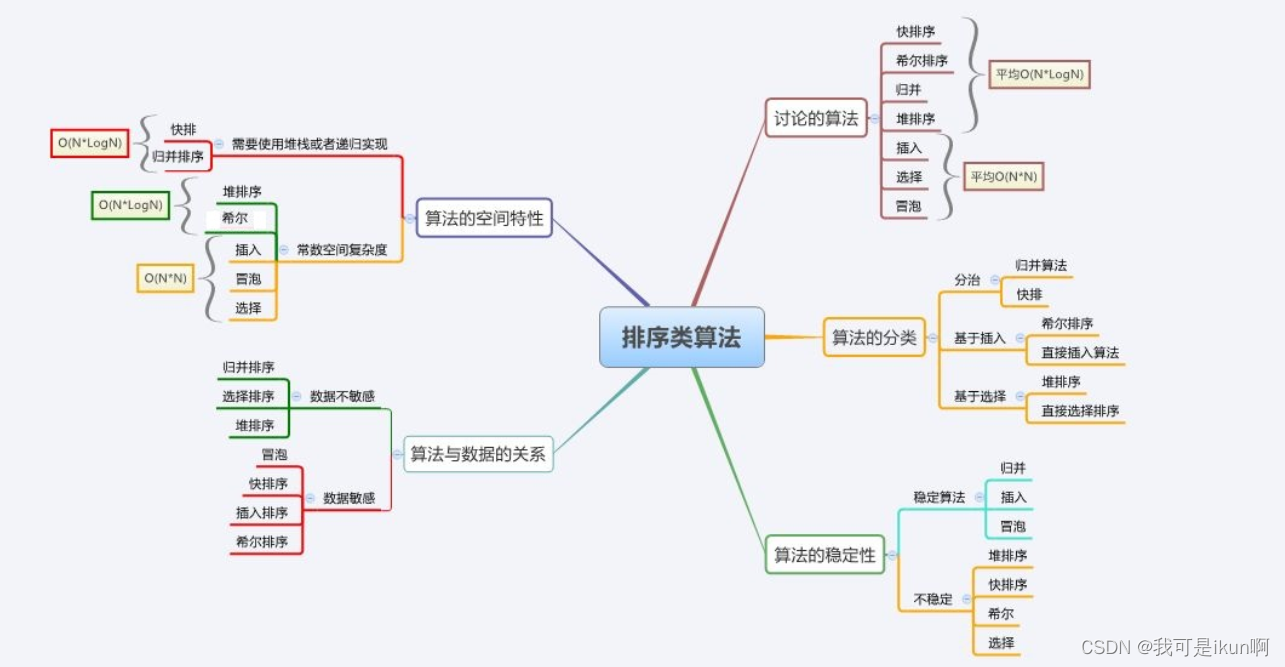
手撕八大排序(下)
目录 交换排序 冒泡排序: 快速排序 Hoare法 挖坑法 前后指针法【了解即可】 优化 再次优化(插入排序) 迭代法 其他排序 归并排序 计数排序 排序总结 结束了上半章四个较为简单的排序,接下来的难度将会大幅度上升&…...
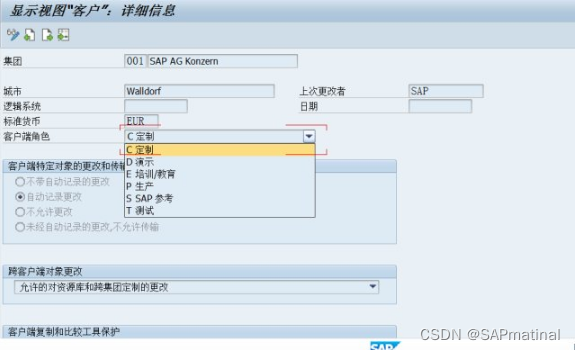
SAP 详细解析SCC4
事务代码:SCC4,选择一个客户端,点击进入,如图: 一、客户端角色 客户控制:客户的角色(生产性,测试,...) 此属性表示 R/3 系统中的客户端角色。其中可能包括…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

作为测试我们应该关注redis哪些方面
1、功能测试 数据结构操作:验证字符串、列表、哈希、集合和有序的基本操作是否正确 持久化:测试aof和aof持久化机制,确保数据在开启后正确恢复。 事务:检查事务的原子性和回滚机制。 发布订阅:确保消息正确传递。 2、性…...

【堆垛策略】设计方法
堆垛策略的设计是积木堆叠系统的核心,直接影响堆叠的稳定性、效率和容错能力。以下是分层次的堆垛策略设计方法,涵盖基础规则、优化算法和容错机制: 1. 基础堆垛规则 (1) 物理稳定性优先 重心原则: 大尺寸/重量积木在下…...
