机器学习基本概念2
资料来源：
https://www.youtube.com/watch?v=Ye018rCVvOo&list=PLJV_el3uVTsMhtt7_Y6sgTHGHp1Vb2P2J&index=1
https://www.youtube.com/watch?v=bHcJCp2Fyxs&list=PLJV_el3uVTsMhtt7_Y6sgTHGHp1Vb2P2J&index=2
分三步
1、 定义function
b和w是需要透过知识去获取的，是未知的
做机器学习，需要Domain Knowledge，这些知识就是用来解b和w
这里的函式，就叫做Model
我们知道2月25号的人数是多少，就叫feauture
2、 定义Loss
Loss is a function of parameters
真实的值叫Label（正确的数值）
可以算出来最近3年的误差，把所有的误差加起来，算出来一个L，这就是我们的Loss，值越大，说明越不好
MAE和MSE的区别和选择具体而定，还有Cross-entropy
真实的后台统计数据例子
越偏红色，代表Loss越大，偏蓝色，Loss越小，那在预测的时候，w为0.75 b代500，可能预测会更准
3、最佳化算法
做法： Gradient Descent
如何做： 当w不同的值时，会得到不同的Loss，
怎么找到w，让Loss最小，随机选取初始化的点 w0（有一些方法可以更科学的找到这个值）
计算w对l的微积分，计算error surface的斜率，如果这个斜率的值为负数，
把w的值变大，Loss就会小
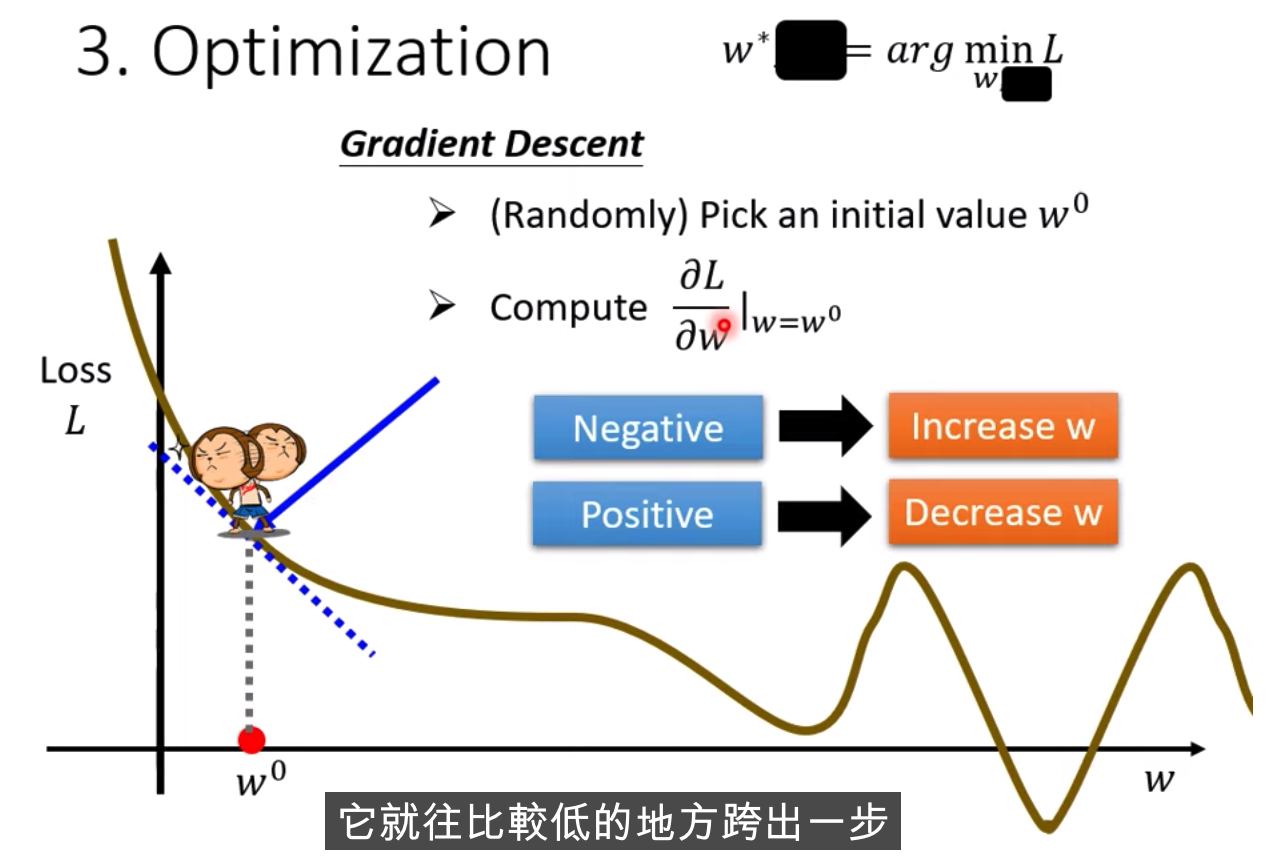
跨步要多大呢？
斜率大，就跨大
学习速率是自己设定的
Loss的值为什么会是负数？
因为这个函数是自己定义的，Loss的定义的估算的值和实际的值的绝对值，如果根据刚刚的定义，不可能为负数
但上面的这个例子不是真实的案例，error surface 可能是任何形状
hyperparameter，自己设定的
什么时候会停止下来？一般两种情况
a、 前期设定了这个参数，例如次数
b、 达到了理想的状态
Gradient Descent上面找不到最佳的loss值，因为随机的位置不一样
Local minima是个假的问题，具体为什么，后面会讲
两个参数，如何做上面的Graddient Descent？
例子
课程总结：
这三个步骤合并起来，叫做训练
2021年的误差还是比较大的，怎么做的更好？ 分析下数据
蓝色线相当于把红色右移了一天而已，每隔7天就是一个循环
这个model是一个比较坏的，我们可以拿7天的周期来进行修改
x叫做feature
上面的叫做Linear Model，我们后面看下怎么把Linear Model做的更好
Linear Model 太过简单了
我们需要写出更复杂，更多未知参数的function
1除以1+Exponential-b+wx1，再乘以constant常数
当b+wx1趋向于无穷大的时候，会发生什么事呢，Exponential会消失，当X1非常大的时候，这一条线会收敛在高度是C的地方
当b+wx1趋向于负的无穷大，分母会非常大，Y的值会趋近于0
S型的function，叫做sigmoid
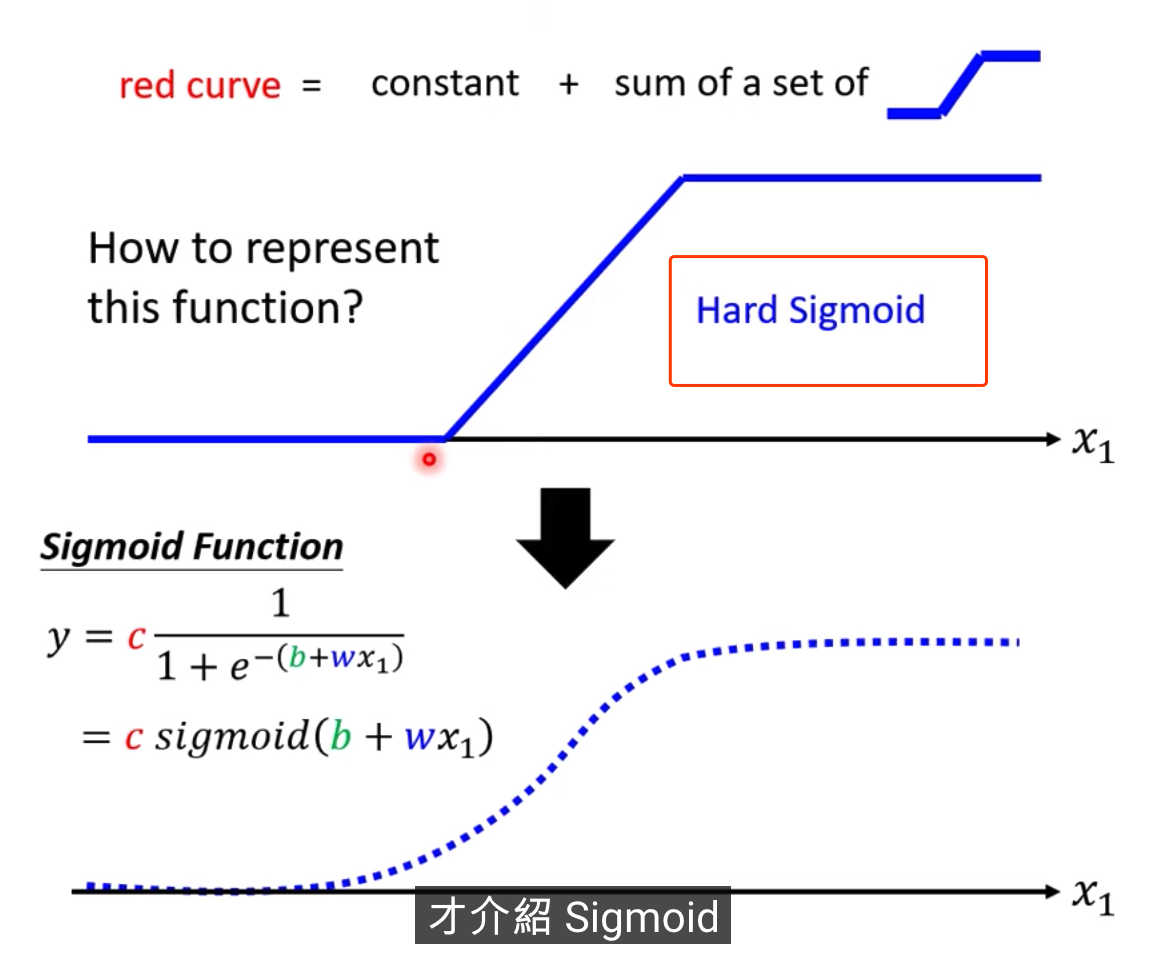
我们需要各式各样合适蓝色的function，那这个蓝色function怎么出来呢，需要调整b和w
改w，会改变斜率，斜坡的坡度
修改b呢，会左右移动
修改c，会改变高度
可以制造出不同
把0和1和2和3都加起来
summation，b是constant
假设b,c,w是未知参数，有弹性，有未知参数的函式
Transpose
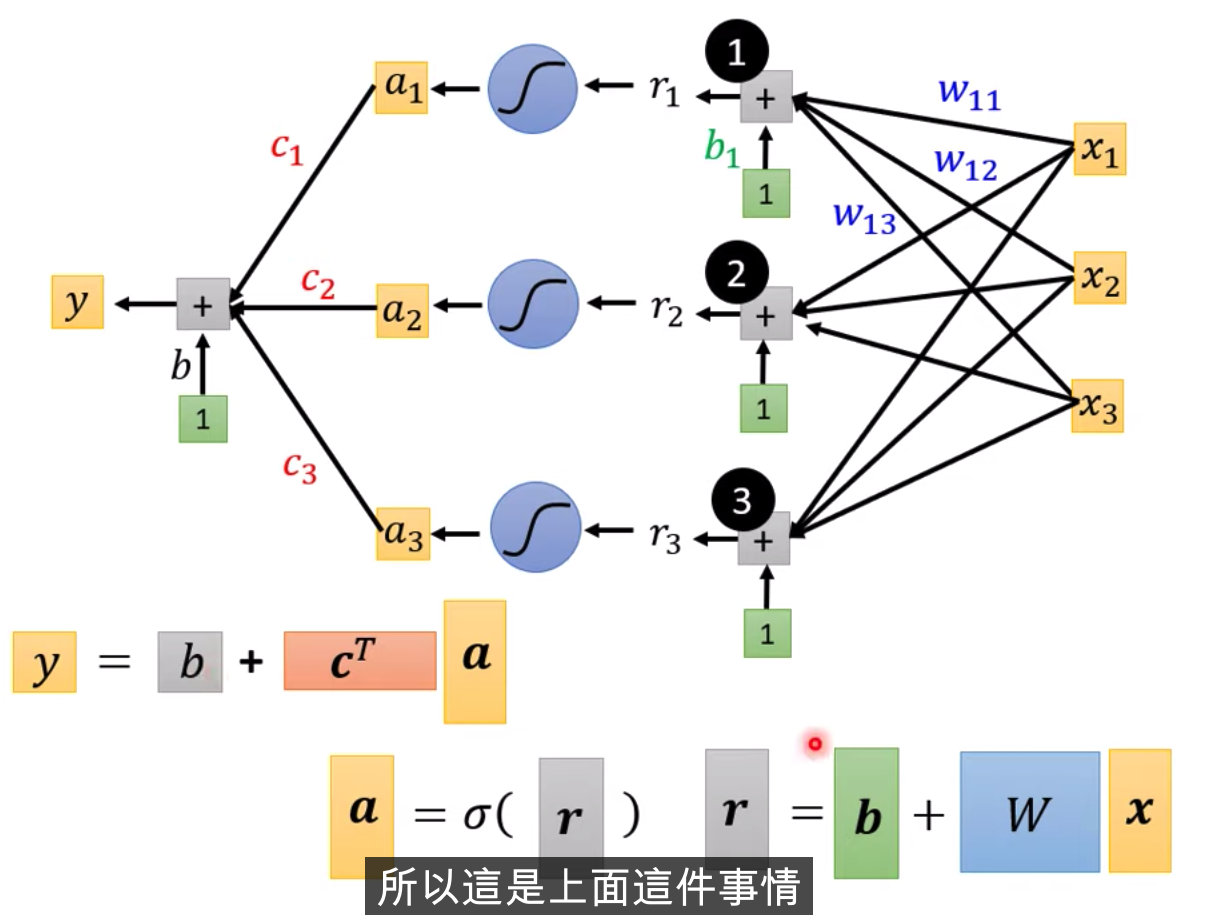
X输入，我们的Feature是X这个向量，X乘上矩阵W加上向量b，得到向量r，再把向量r，通过Sigmooid Function得到向量a，
再把向量a跟乘上c的Transpose加上b，就得到了y
不同的表示方式，上面是图示化的方式，下面是线性代数的表示方式
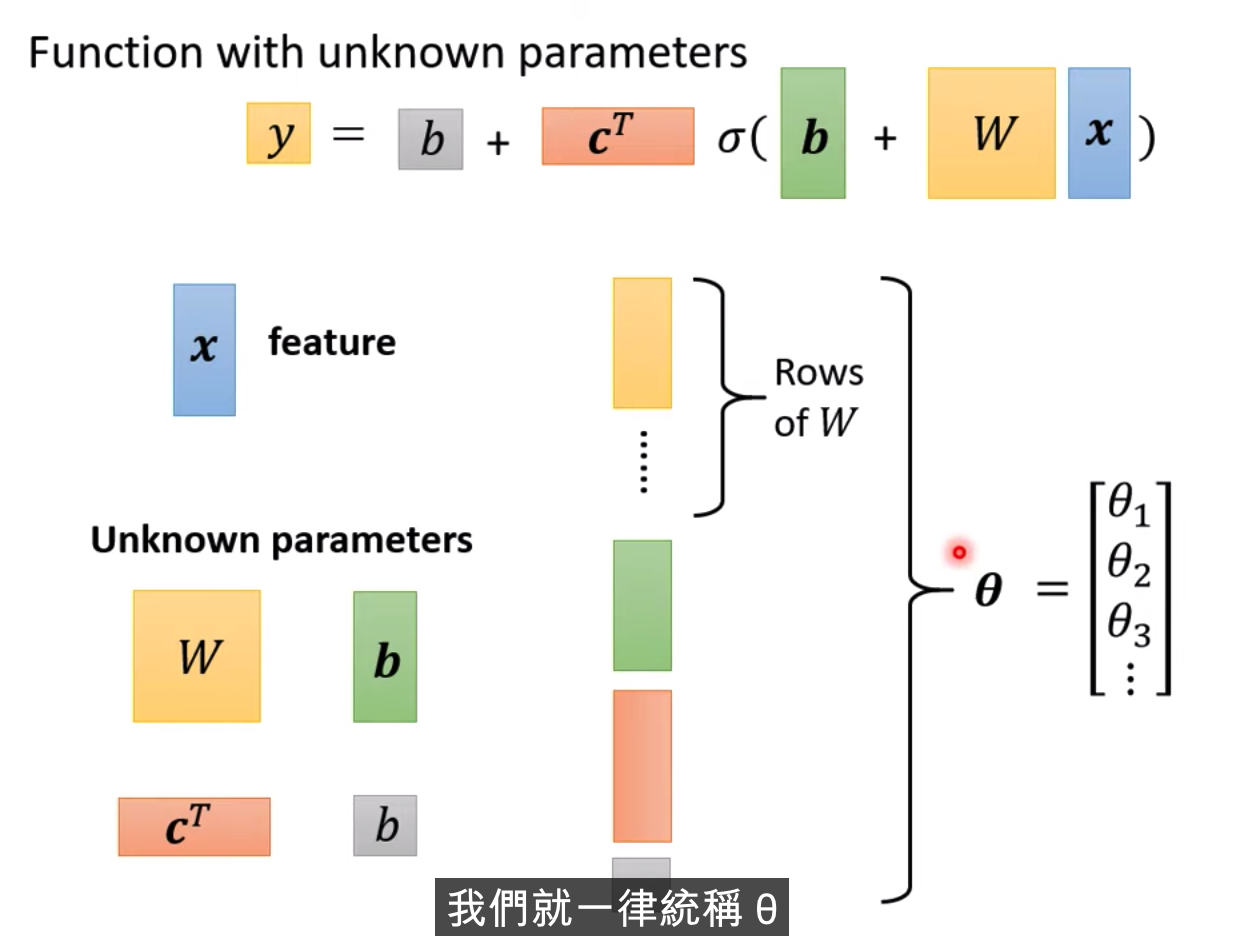
在参数小的情况下，穷举所有的可能就行，不需要使用Gradient Descent
Sigmoid 可以有多个，会产生越多线段的 Piecewise Linear的function，你就可以逼近越复杂的function
至于需要几个Sigmoid，这是另外的Hyper Parameter，这个自己决定
Loss function
Update和Epoch是不一样的东西
每次更新一次参数叫做一次update，把所有的Batch都看过一遍，叫做一个Epoch
为什么要分成一个一个的batch？
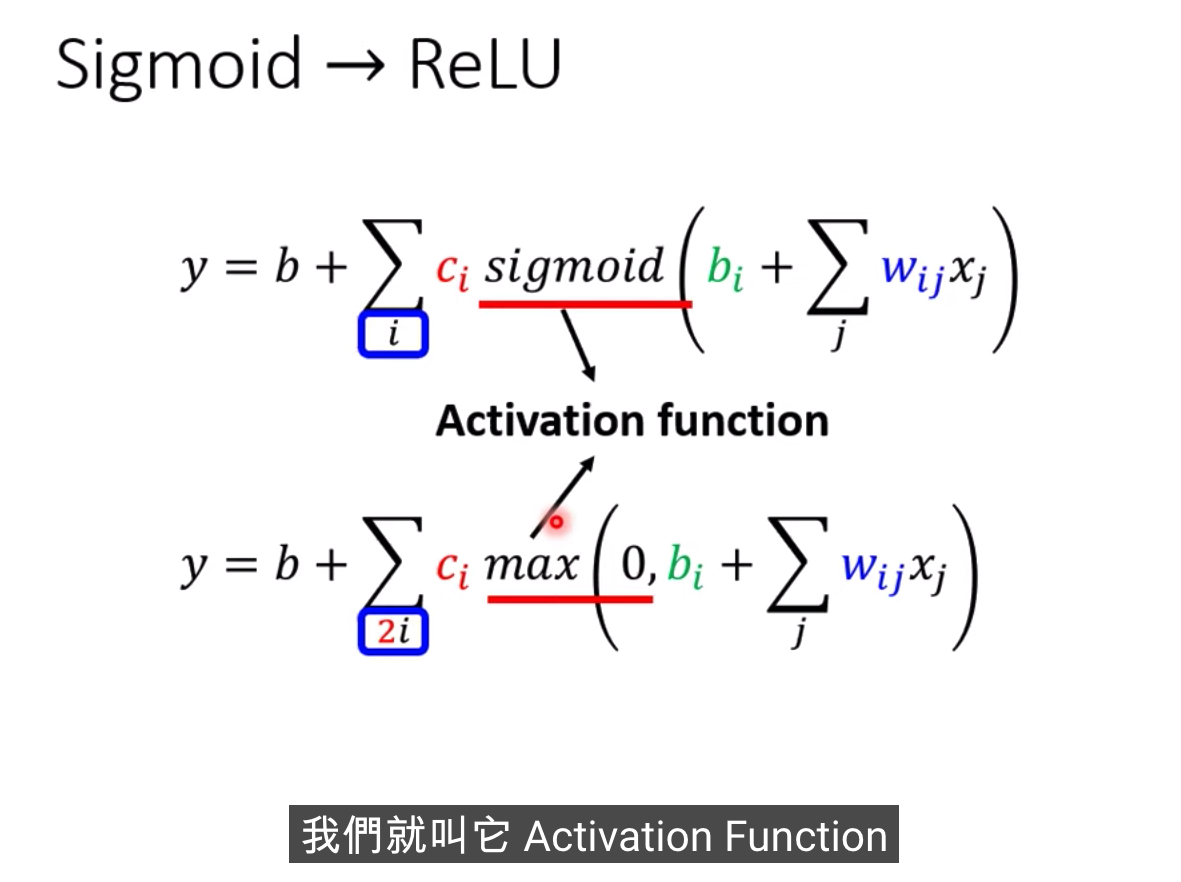
激活函数
哪种比较好？？ Relu好一些
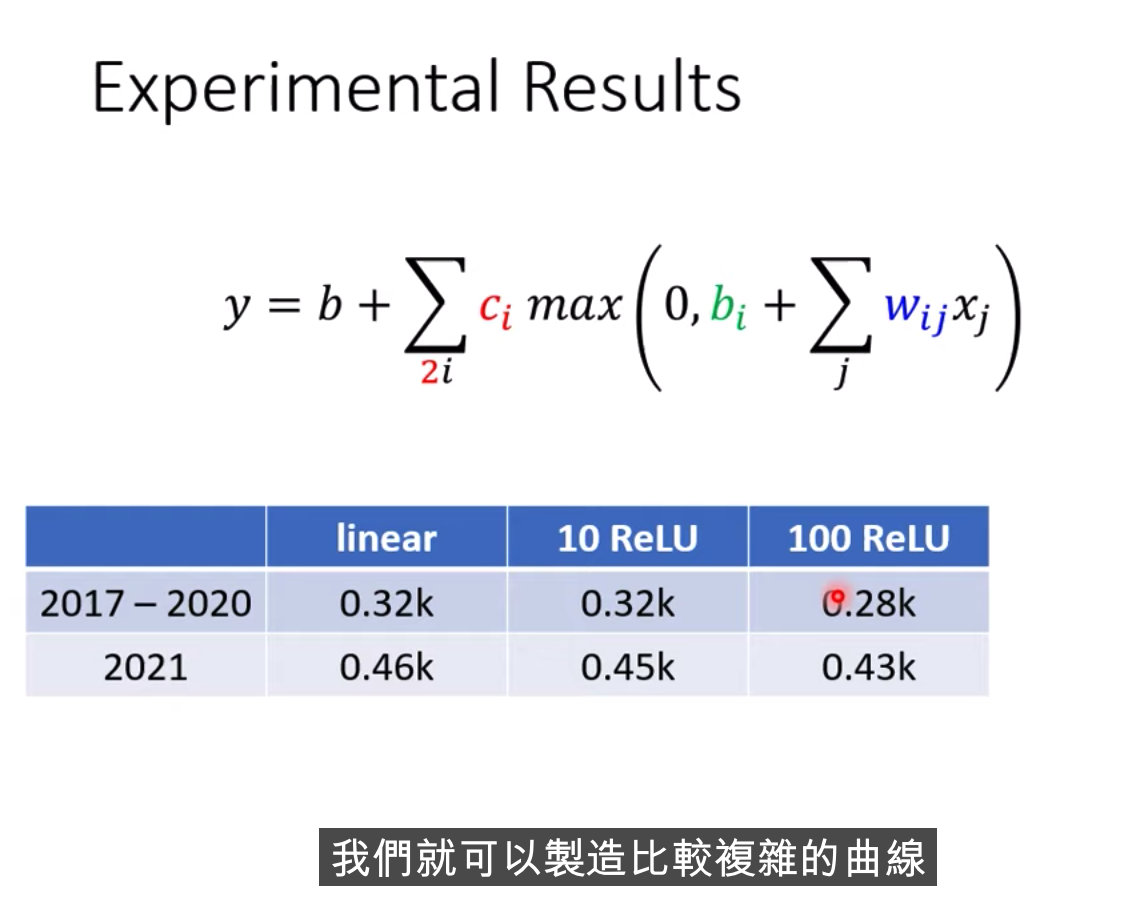
我们还可以继续改我们的模型
我们可以把重复的事情，反复的再多做几次，这里的几次，又是另外一个超参数
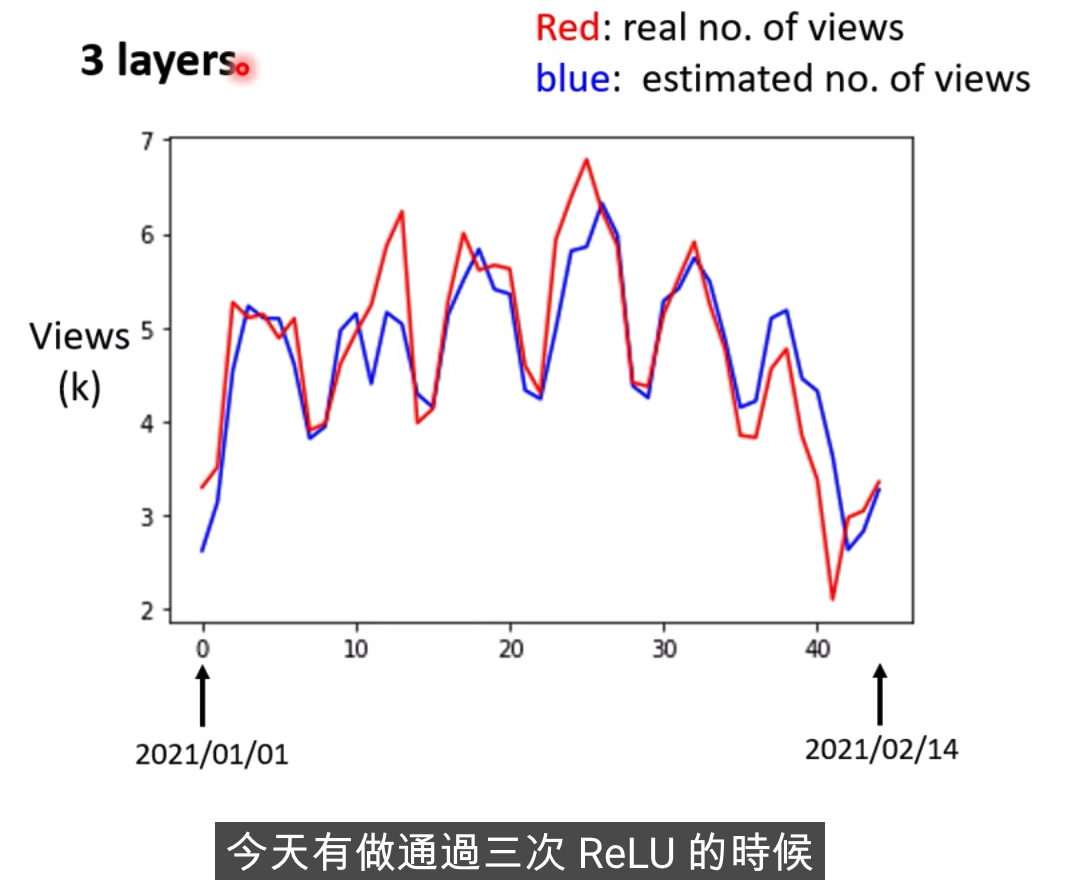
模型也需要一个好的名字
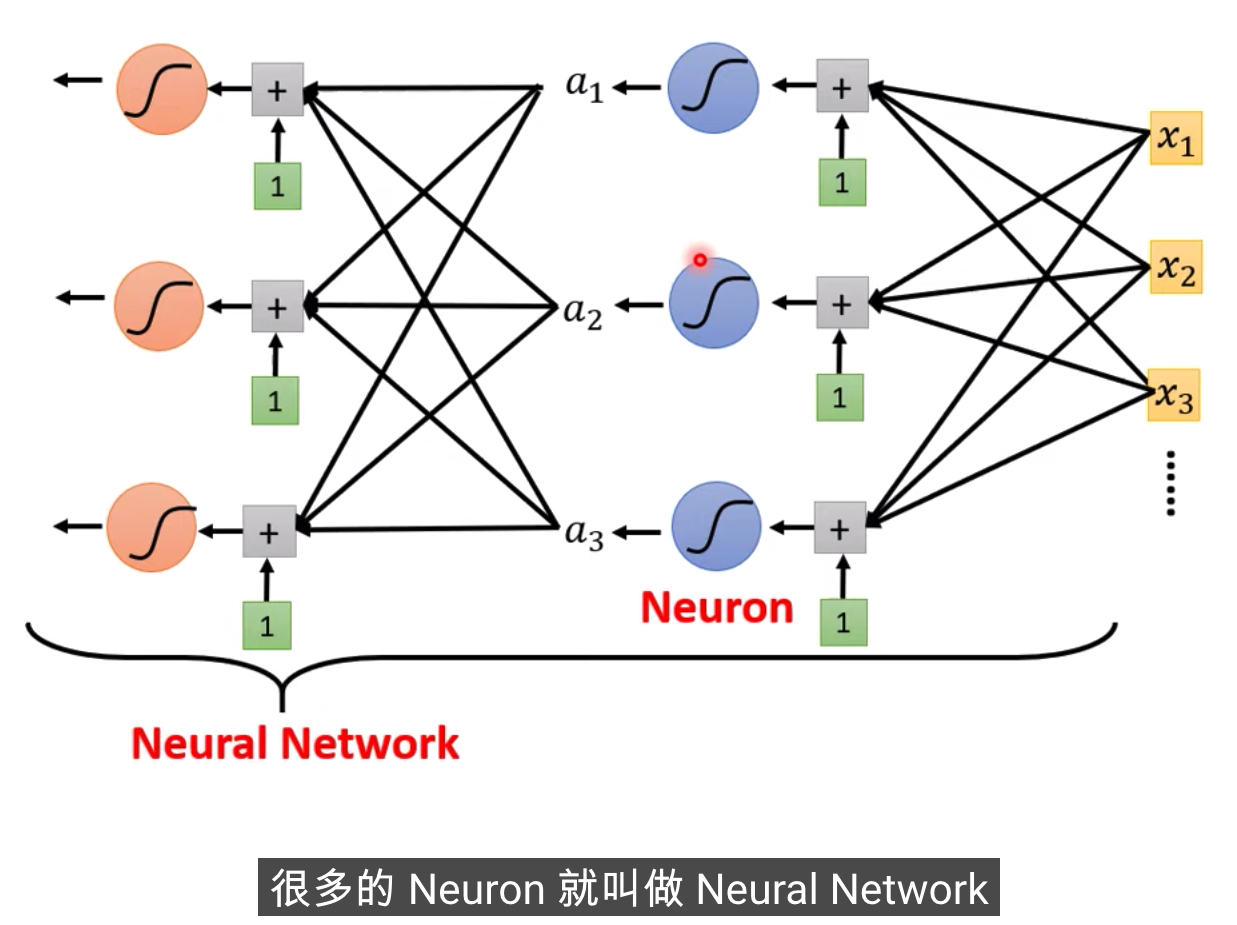
这个是在模拟人脑
Deep Learning的由来。。。。
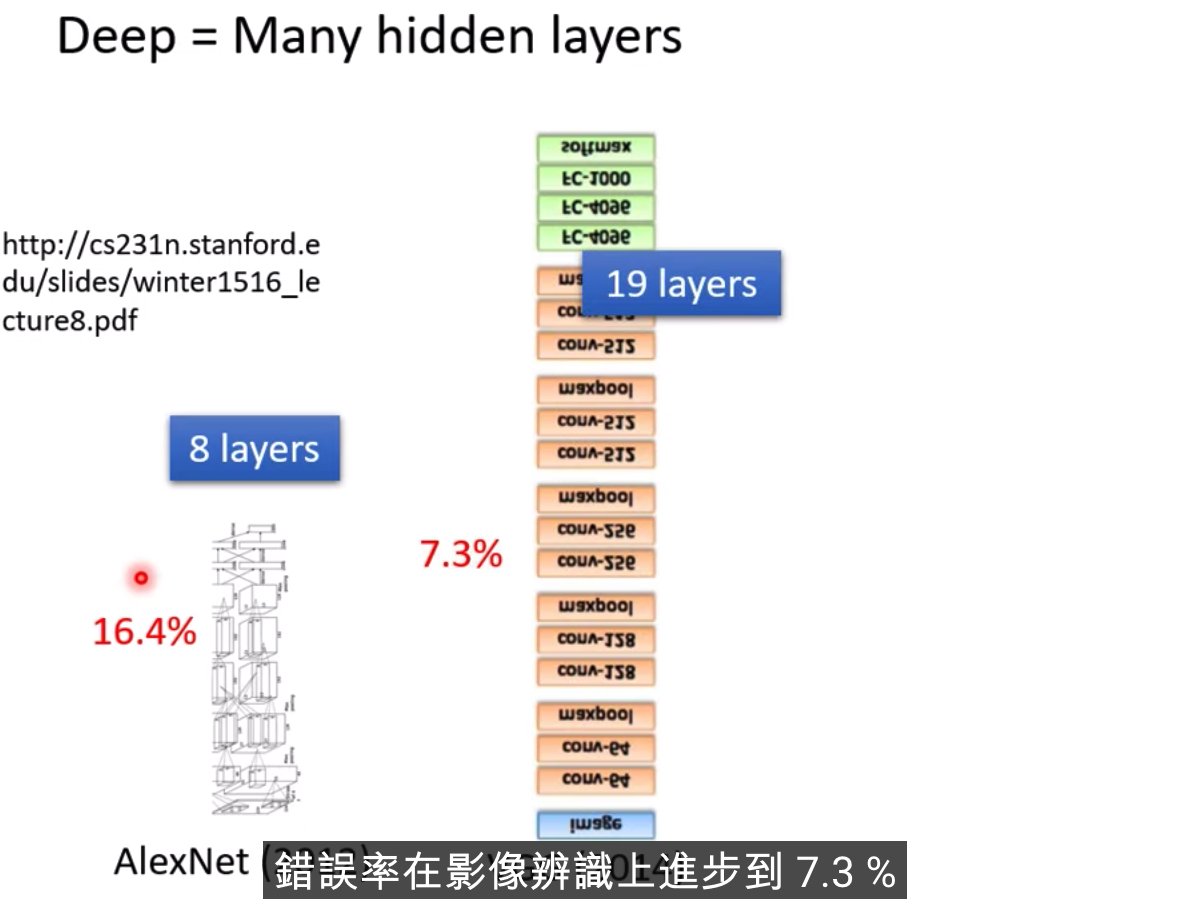
只要有足够多的ReLU或者Sigmoid，就能够逼近任何连续的Function
反复用的意义在哪里？
过多的层数效果不一定好
神经网络结构那部分讲的太精彩了。从简单的线性回归开始，到用几个简单线性函数去逼近一个分段线性函数，然后提出用sigmooid和线性逼近曲线，然后自然而然引出神经网络的基本结构。输入特征，参数，激活函数..等等概念自然而然都出来了
相关文章：
机器学习基本概念2
资料来源： https://www.youtube.com/watch?vYe018rCVvOo&listPLJV_el3uVTsMhtt7_Y6sgTHGHp1Vb2P2J&index1 https://www.youtube.com/watch?vbHcJCp2Fyxs&listPLJV_el3uVTsMhtt7_Y6sgTHGHp1Vb2P2J&index2 分三步 1、 定义function b和w是需要透…...
Spring Cloud 与微服务学习总结（19）—— Spring Cloud Alibaba 之 Nacos 2.3.0 史上最大更新版本发布
Nacos 一个用于构建云原生应用的动态服务发现、配置管理和服务管理平台，由阿里巴巴开源，致力于发现、配置和管理微服务。说白了，Nacos 就是充当微服务中的的注册中心和配置中心。 Nacos 2.3.0 新特性 1. 反脆弱插件 Nacos 2.2.0 版本开始加入反脆弱插件，从 2.3.0 版本开…...
八、C#笔记
/// <summary> /// 第十三章：创建接口和定义抽象类 /// </summary> namespace Chapter13 { class Program { static void Main(string[] args) { //13.1理解接口 ///13.1.1定义接口 ///…...
利用Node.js和cpolar实现远程访问，无需公网IP和路由器设置的完美解决方案
文章目录 前言1.安装Node.js环境2.创建node.js服务3. 访问node.js 服务4.内网穿透4.1 安装配置cpolar内网穿透4.2 创建隧道映射本地端口 5.固定公网地址 前言 Node.js 是能够在服务器端运行 JavaScript 的开放源代码、跨平台运行环境。Node.js 由 OpenJS Foundation࿰…...
C++如何通过调用ffmpeg接口对H264文件进行编码和解码
C可以通过调用FFmpeg的API来对H264文件进行编码和解码。下面是一个简单的例子。 首先需要在代码中包含FFmpeg的头文件： extern "C" { #include <libavcodec/avcodec.h> #include <libavformat/avformat.h> #include <libswscale/swscale…...
使用MetaMask + Ganache搭建本地私有网络并实现合约部署与互动
我使用Remix编写合约，MetaMask钱包工具和Ganache搭建了一个私有网络，并且实现了合约的部署和互动。 在前面的博客中提到了 Remix在线环境及钱包申请 以及 Solidity的基本语法 ，没看过的小伙伴可以点击链接查看一下，都是在本专栏下…...
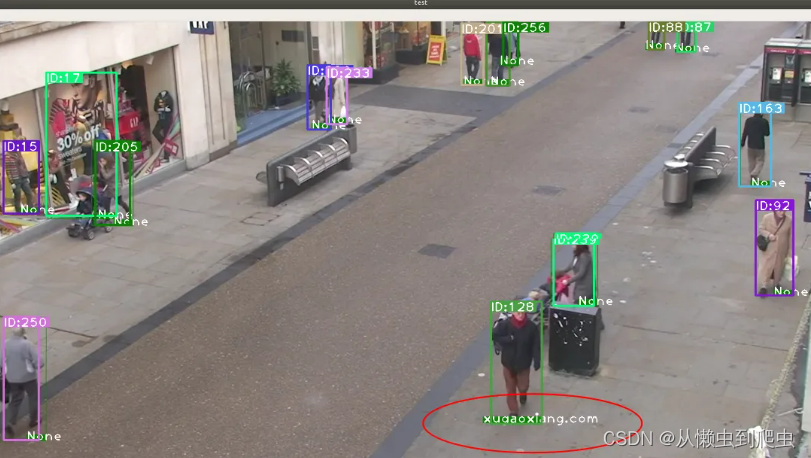
目标检测、目标跟踪、重识别
文章目录 环境前言项目复现特征提取工程下载参考资料 环境 ubuntu 18.04 64位yolov5deepsortfastreid 前言 基于YOLOv5和DeepSort的目标跟踪 介绍过针对行人的检测与跟踪。本文介绍另一个项目，结合 FastReid 来实现行人的检测、跟踪和重识别。作者给出的2个主…...
高防IP防御效果怎么样，和VPN有区别吗
高防IP主要是用于防御网络攻击，可以抵御各种类型的DDoS攻击，隐藏源IP地址，提高网络安全性和用户体验。主要目的是解决外部网络攻击问题，保护网络安全，避免因攻击而导致的业务中断和数据泄露等问题。 而VPN则是一种可以…...
探秘MSSQL存储过程：功能、用法及实战案例
在现代软件开发中，高效地操作数据库是至关重要的。而MSSQL（Microsoft SQL Server）作为一款强大的关系型数据库管理系统，为我们提供了丰富的功能和工具来处理数据。其中，MSSQL存储过程是一项强大而又常用的功能…...
我们常说的流应用到底是什么？
流应用是DCloud公司开发的一种可以让手机App安装包实现边用边下的技术。基于HTML5规范的即点即用应用，开发者按照HTML5规范开发的应用，可以在支持HTML5流应用的发行渠道实现即点即用的效果。 流应用是基于 HTML5规范的即点即用应用，开发者按照…...
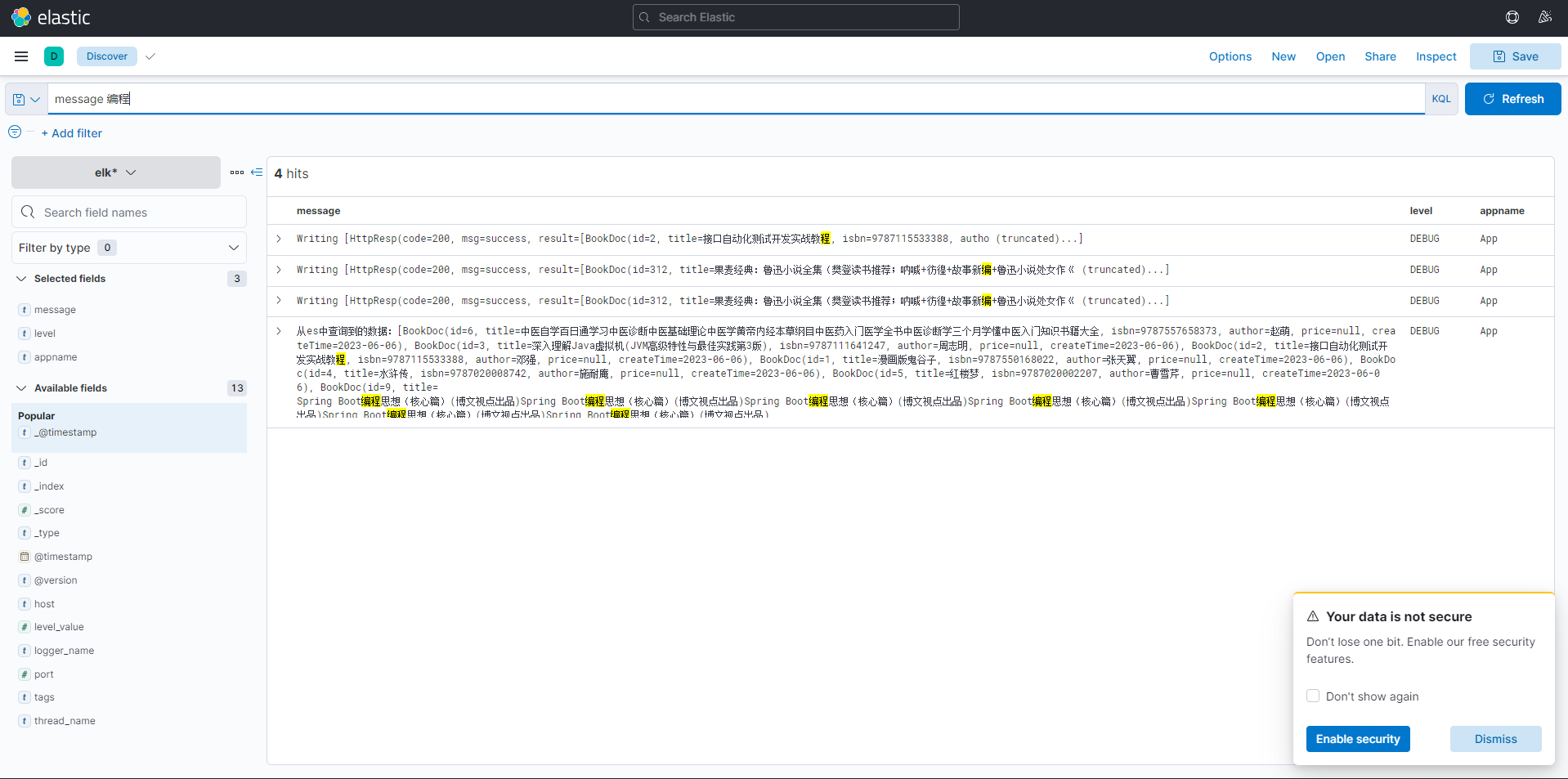
ELK 日志解决方案
ELK 是目前最流行的集中式日志解决方案，提供了对日志收集、存储、展示等一站式的解决方案。 ELK 分别指 Elasticsearch、Logstash、Kibana。 Elasticsearch：分布式数据搜索引擎，基于 Apache Lucene 实现，可集群，提供…...
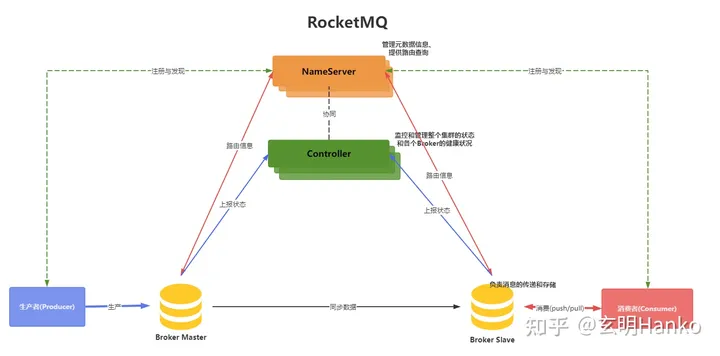
本项目基于Spring boot的AMQP模块，整合流行的开源消息队列中间件rabbitMQ,实现一个向rabbitMQ
在业务逻辑的异步处理，系统解耦，分布式通信以及控制高并发的场景下，消息队列有着广泛的应用。本项目基于Spring的AMQP模块，整合流行的开源消息队列中间件rabbitMQ,实现一个向rabbitMQ添加和读取消息的功能。并比较了两种模式&…...
freeswitch webrtc video_demo客户端进行MCU的视频会议
系统环境 一、编译服务器和加载模块 二、下载编译指定版本video_demo 三、配置verto.conf.xml 1.修改配置文件 2.重新启动 四、MCU通话测试 1.如何使用video_demo 2.测试结果 五、MCU的通话原理及音频/视频/布局/管理员等参数配置 附录 freeswitch微信交流群 系统环境 lsb_rel…...
【鸿蒙学习网络】
鸿蒙技术学习相关学习资料 官方文档：华为官方提供了鸿蒙开发者文档，包括开发指南、API参考和示例代码等。您可以访问华为开发者中心网站（https://developer.harmonyos.com/）获取最新的官方文档和教程。在 线 课 程 ： …...
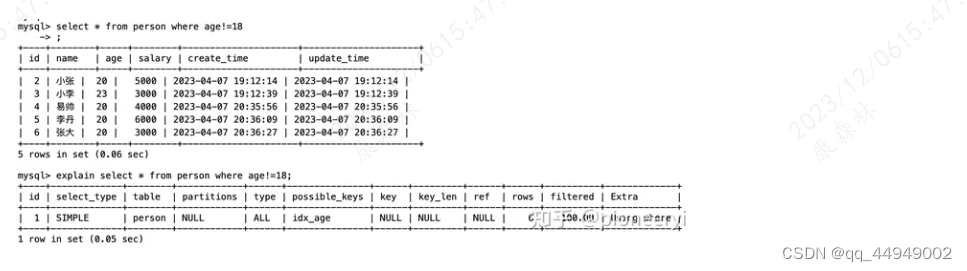
MySQL系列（一）：索引篇
为什么是B树？ 我们推导下，首先看下用哈希表做索引，是否可以满足需求。如果我们用哈希建了索引，那么对于如下这种SQL，通过哈希，可以快速检索出数据： select * from t_user_info where id1;但是这…...
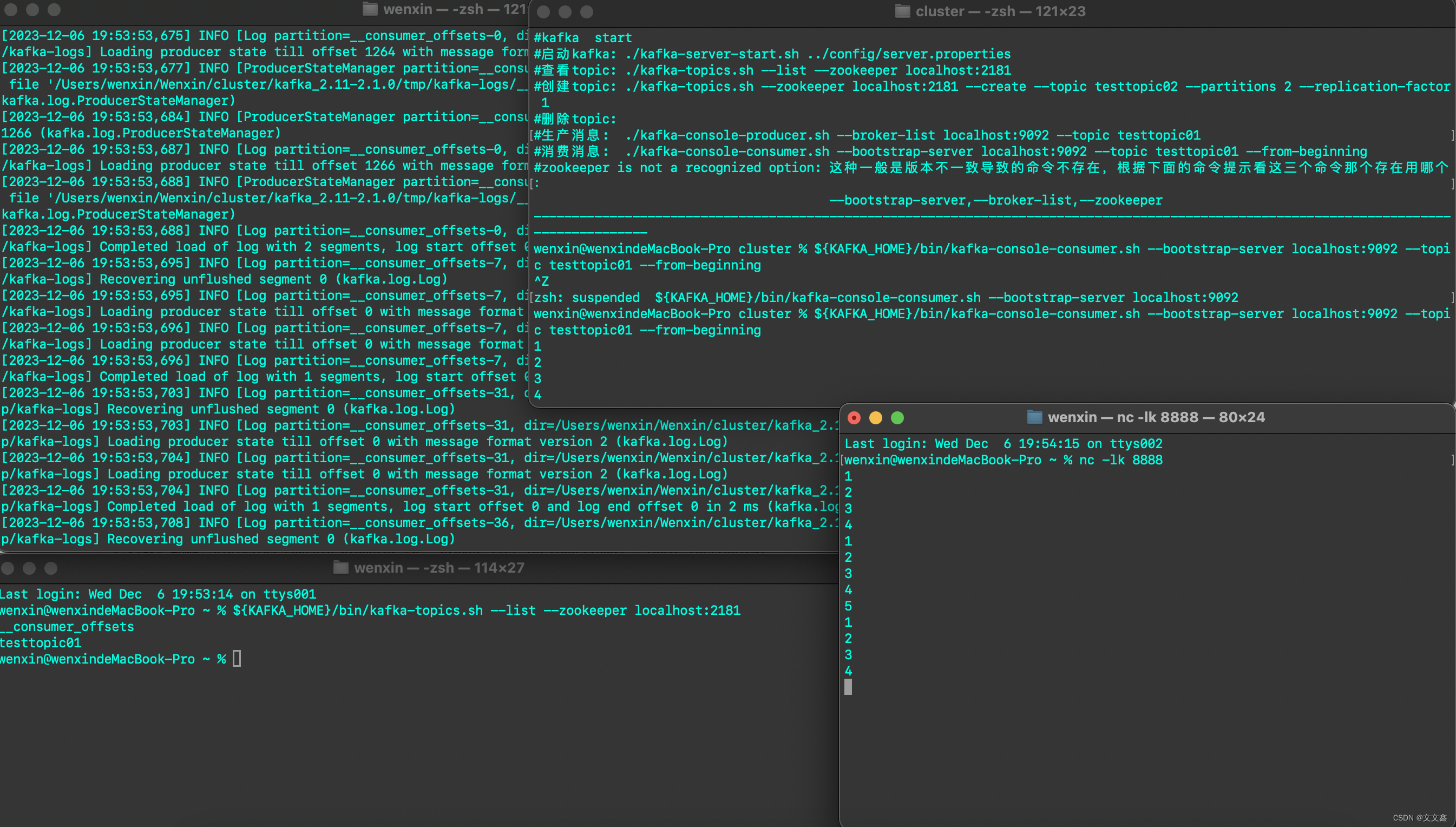
Flink Flink数据写入Kafka
一、环境准备 官网地址 flink官方集成了通用的 Kafka 连接器，使用时需要根据生产环境的版本引入相应的依赖 <properties><project.build.sourceEncoding>UTF-8</project.build.sourceEncoding><flink.version>1.14.6</flink.version&g…...
《论文阅读》用于情绪回复生成的情绪正则化条件变分自动编码器 Affective Computing 2021
《论文阅读》用于情绪回复生成的情绪正则化条件变分自动编码器 前言简介模型结构实验结果总结前言 今天为大家带来的是《Emotion-Regularized Conditional Variational Autoencoder for Emotional Response Generation》 出版：IEEE Transactions on Affective Computing 时间…...
Pytorch CIFAR10图像分类 Swin Transformer篇
Pytorch CIFAR10图像分类 Swin Transformer篇 文章目录 Pytorch CIFAR10图像分类 Swin Transformer篇4. 定义网络（Swin Transformer）Swin Transformer整体架构Patch MergingW-MSASW-MSARelative position biasSwin Transformer 网络结构Patch EmbeddingP…...
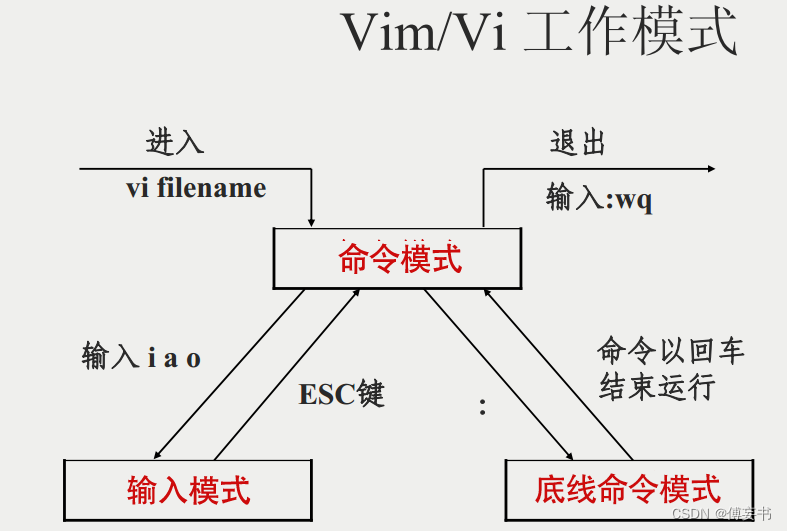
【vim】常用操作
用的时候看看，记太多也没用，下面都是最常用的，更多去查文档vim指令集。 以下均为正常模式下面操作，正在编辑的，先etc一下. 1/拷贝当前行 yy，5yy为拷贝包含当前行往下五行 2/p将拷贝的东西粘贴到当前行下…...
oracle、误操作删除数据库 数据恢复。
–查询 执行 delete 的语句 ，拿到删除的时间 FIRST_LOAD_TIME ，删除行数可参考 ROWS_PROCESSED select t.FIRST_LOAD_TIME,t.ROWS_PROCESSED,t.* from v$sql t where t.sql_text like %delete from trade% ;select *from trade as of timestamp to_time…...
多模态2025：技术路线“神仙打架”，视频生成冲上云霄
文｜魏琳华 编｜王一粟 一场大会，聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中，汇集了学界、创业公司和大厂等三方的热门选手，关于多模态的集中讨论达到了前所未有的热度。其中，…...
脑机新手指南（八）：OpenBCI_GUI：从环境搭建到数据可视化（下）
一、数据处理与分析实战 （一）实时滤波与参数调整 基础滤波操作 60Hz 工频滤波：勾选界面右侧 “60Hz” 复选框，可有效抑制电网干扰（适用于北美地区，欧洲用户可调整为 50Hz）。 平滑处理&…...
cf2117E
原题链接：https://codeforces.com/contest/2117/problem/E 题目背景： 给定两个数组a,b，可以执行多次以下操作：选择 i (1 < i < n - 1)，并设置 或，也可以在执行上述操作前执行一次删除任意 和 。求…...
css的定位（position）详解：相对定位 绝对定位 固定定位
在 CSS 中，元素的定位通过 position 属性控制，共有 5 种定位模式：static（静态定位）、relative（相对定位）、absolute（绝对定位）、fixed（固定定位）和…...
Java入门学习详细版（一）
大家好，Java 学习是一个系统学习的过程，核心原则就是“理论 实践 坚持”，并且需循序渐进，不可过于着急，本篇文章推出的这份详细入门学习资料将带大家从零基础开始，逐步掌握 Java 的核心概念和编程技能。 …...
人工智能（大型语言模型 LLMs）对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验，我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育，这并非炒作，而是已经发生的巨大变革。教育机构和教育者不能忽视它，试图简单地禁止学生使…...
基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化（Gradient Normalization） (2) 判别器梯度间隙正则化（Discriminator Gradient Gap Regularization） (3) 自注意力机制（Self-Attention） 3. 完整损失函数 二…...
代码规范和架构【立芯理论一】（2025.06.08）
1、代码规范的目标 代码简洁精炼、美观，可持续性好高效率高复用，可移植性好高内聚，低耦合没有冗余规范性，代码有规可循，可以看出自己当时的思考过程特殊排版，特殊语法，特殊指令，必须…...
解决：Android studio 编译后报错\app\src\main\cpp\CMakeLists.txt‘ to exist
现象： android studio报错： [CXX1409] D:\GitLab\xxxxx\app.cxx\Debug\3f3w4y1i\arm64-v8a\android_gradle_build.json : expected buildFiles file ‘D:\GitLab\xxxxx\app\src\main\cpp\CMakeLists.txt’ to exist 解决： 不要动CMakeLists.…...
tauri项目，如何在rust端读取电脑环境变量
如果想在前端通过调用来获取环境变量的值，可以通过标准的依赖： std::env::var(name).ok() 想在前端通过调用来获取，可以写一个command函数： #[tauri::command] pub fn get_env_var(name: String) -> Result<String, Stri…...