美易官方:投资美股证券投资组合的优势及快速上手指南
投资美股证券投资组合的优势及快速上手指南

美股证券投资组合的优势
美国股市一直以来都是全球投资者的热门选择之一。与其他市场相比,美国股市具有诸多优势,如市场规模大、流动性好、信息透明度高等。投资者在美国股市中,可以选择各种不同类型的证券进行投资,包括股票、债券、期货等,从而实现投资组合的多样化。同时,美国证券交易操作界面简单便捷,出入金方便,并且免入金门槛,还可以进行杠杆操作。对于想要进入美国股市投资的人来说,如何快速上手成为了一个重要问题。在当今这个信息化、网络化的时代,投资已经不再是少数人的专利,越来越多的人开始通过各种渠道进行财富管理和增值。美易官方投资平台作为行业内的佼佼者,以其卓越的安全性、可靠性和便捷性,成为了广大投资者信赖的选择。

快速上手指南
1.
选择可靠安全的证券交易平台 在进入美国股市投资之前,首先需要选择一个可靠安全的证券交易平台。确保平台具有相关监管牌照,并且注册用户手续简单便捷。
2.
多样化投资组合 在进行美国股市投资时,建议投资者将资金分散到不同类型的证券中,实现投资组合的多样化。这样可以降低风险,并且能够在不同市场情况下获得更好的回报。
3.
简单操作界面 选择一个操作界面简单便捷的交易平台对于新手来说非常重要。这样可以让投资者更快地了解交易规则和操作流程,并且更容易上手进行交易。
4.
出入金方便 一个好的证券交易平台应该提供出入金方便快捷的服务。这样可以让投资者在需要时随时进行充值或提现操作。
5.
免入金门槛 对于新手来说,免入金门槛是一个很大的吸引力。这意味着即使是小额资金也能够进入美国股市进行投资。
6.
杠杆操作 一些证券交易平台还提供杠杆操作功能,这意味着可以借用额外的资金进行交易。但是需要注意,在使用杠杆操作时要谨慎,因为风险也会相应增加。
美易全球投资中心副总裁Kenny Jolin表示通过选择可靠安全的证券交易平台、建立多样化投资组合、使用简单便捷的操作界面、享受出入金方便和免入金门槛等优势,在了解相关风险和规则后,在美国股市中进行快速上手成为可能。希望本文能够帮助想要进入美国股市投资领域的读者们更好地了解并利用这些优势。
相关文章:

美易官方:投资美股证券投资组合的优势及快速上手指南
投资美股证券投资组合的优势及快速上手指南 美股证券投资组合的优势 美国股市一直以来都是全球投资者的热门选择之一。与其他市场相比,美国股市具有诸多优势,如市场规模大、流动性好、信息透明度高等。投资者在美国股市中,可以选择各种不同类…...

centos日常运维随记
# 需要生成随机字符及数字 rootAAA:~# echo $RANDOM | md5sum |cut -c 3-29 e7e8942a791146531f613c7c757 # echo $RANDOM 产生随机数据 # md5sum 随机数生成md5值 # cut -c 3-29 :md5产生的是32的md5数,使用cut -c 对这个数进行 第3位到第29位的截取# 在现有的…...
)
设计模式之观察者模式(主题对象发生变化,通知各个观察者)
当涉及到电商场景时,观察者模式可以用于处理多种情况,比如订单状态更新、库存变化、用户积分变化等。下面是一个简化的订单状态更新的观察者模式案例。 1.首先,定义一个主题接口 OrderSubject /*** Description:主题,用于管理观察…...

vue+高德,百度地图
1,npm安装vue-amap npm install vue-amap --save 2,main.js引入 import VueAMap from vue-amap; Vue.use(VueAMap); VueAMap.initAMapApiLoader({key: ,plugin: [AMap.Autocomplete, AMap.PlaceSearch, AMap.Scale, AMap.OverView, AMap.ToolBar, AMap.…...
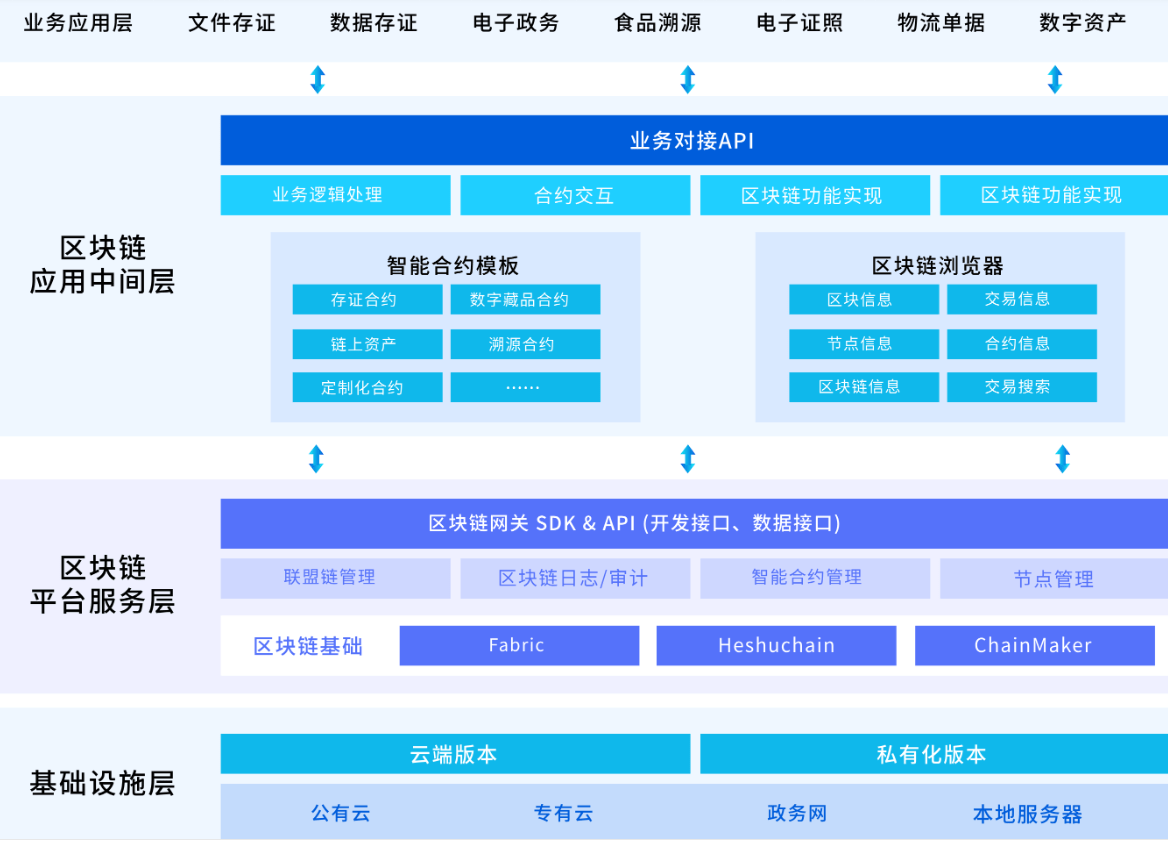
工信部举行发布会 数字化产业推动元宇宙发展取得良好成效
据官方消息,工业和信息化部12日举行“发挥国家高新区作用 加快推进新型工业化”新闻发布会。 在数字化建设方面取得了良好的成绩: 一是数字经济加速发展。国家高新区着力推动人工智能、大数据、云计算、区块链和元宇宙等新产业新业态蓬勃发展ÿ…...
有没有手机电脑同步的工作时间管理软件?
越来越多的职场人士感到每天的工作任务是比较多的,而工作时间又是有限的,所以经常时间不够用。因此,对于上班族来说,高效的时间管理是提高工作效率、按时完成任务的关键。为了满足这一需求,很多网友都在寻找一款既能在…...

docker安装及简单使用(Linux版本)
文章目录 前言一、docker安装二、docker命令pull(安装镜像)rmi(删除镜像)images(查看镜像)run(创建容器)删除容器exec(进入运行中的容器)常用命令 总结如有启…...

山西电力市场日前价格预测【2023-12-10】
1.日前价格预测 预测说明: 如上图所示,预测明日(2023-12-10)山西电力市场全天平均日前电价为384.75元/MWh。其中,最高日前价格为493.66元/MWh,预计出现在16: 00。最低日前电价为282.24元/MWh,预…...

在OpenCV基于深度学习的超分辨率模型实践
1. 引言 OpenCV是一个开源的计算机视觉库,拥有大量优秀的算法。基于最新的合并,OpenCV包含一个易于使用的接口,主要用于实现基于深度学习方法的超分辨率(SR)。该接口包含预先训练的模型,这些模型可以非常容…...
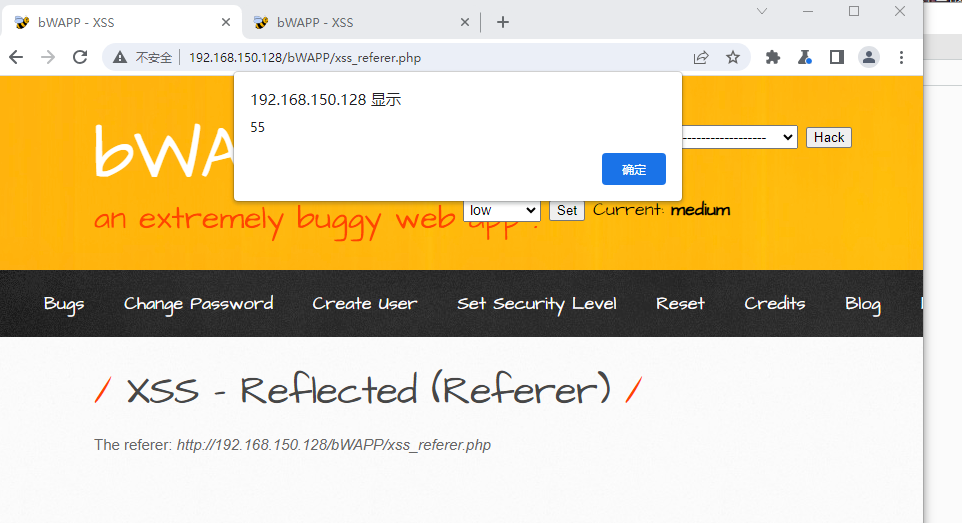
beebox靶场A3 中等级别 xss通关教程
特别注意,低级和中级的差别在于中级使用了一些函数进行了过滤或转义字符 例如 addslashes() 函数返回在预定义字符之前添加反斜杠的字符串。 预定义字符是: 单引号()双引号(")反斜杠(\&…...
———Django与Ajax)
前端知识笔记(二)———Django与Ajax
特点: 异步提交 局部刷新 例子:github注册 动态获取用户名实时的跟后端确认并实时的展示到前端(局部刷新) 朝后端发送请求的方式 1.浏览器地址栏直接输入url回车 -----》get请求 2.a标签的href属性 -----》get请求 3…...
C++新经典模板与泛型编程:用成员函数重载实现is_base_of
用成员函数重载实现is_base_of std::is_base_of是一个C 11标准中用于判断某个类是否是另一个类父类的类模板。 #include "killCmake.h"#include<string>using namespace std;class A { };class B : public A { public:B(int x): x_(x){} private:int x_; };/…...

【vue3】处理数组方法,在数组中获取指定条件所在的数组对象等持续更新笔记~~
1、在数组中获取指定条件所在的数组对象 (1)filter方法获取到的是包含指定项的数组 data.checkRow res.result.filter(item > item.checked 1);打印: (2)map方法取到的是包含指定项的数组,如果满足…...

digit函数
题目描述 在程序中定义一函数 digit(n,k),它能分离出整数 n 从右边数第 k 个数字。 输入格式 正整数 n 和 k。 输出格式 一个数字。 输入输出样例 输入 #1 31859 3 输出 #1 8 说明/提示 n≤10^9。 k≤10。 因为用整数n来做有点难,所以我用…...

Linux中的堡垒机搭建以及使用
JumpServer搭建 安装应用包 curl -sSL https://resource.fit2cloud.com/jumpserver/jumpserver/releases/latest/download/quick_start.sh | bash 一路回车即可安装完毕(可根据需求更改) JumpServer的 配置文件路径 /opt/jumpserver/config/config.tx…...

ubuntu安装微信客户端
安装 Wine 环境 Wine环境包下载地址:http://archive.ubuntukylin.com/software/pool/partner/ukylin-wine_70.6.3.25_amd64.deb 下载完安装包后在命令行运行以下命令安装环境: sudo apt-get install -f -y ./ukylin-wine_70.6.3.25_amd64.deb 安装微信…...

ajax清空所有表单内容,包括input标签、单选框radio、多选框CheckBox、下拉框select以及文本域内容
为了实现重置并清空表单内容,你可以使用 jQuery 的 val 方法将各种表单元素的值设置为空字符串,并通过 layui 的 form.render 方法来更新表单的渲染。以下是修改后的代码: layui.use(["form", "laydate", "jquery&…...

通配符用法
在本篇文章中,本文将说明通配符用法。 (1)概述 通配符是在Linux命令中用于匹配文件名的特殊字符。它们可以帮助我们快速定位和操作文件。本文将介绍一些常用的通配符及其示例用法。 通配符是一种用于模式匹配的特殊字符。在计算机领域中&am…...
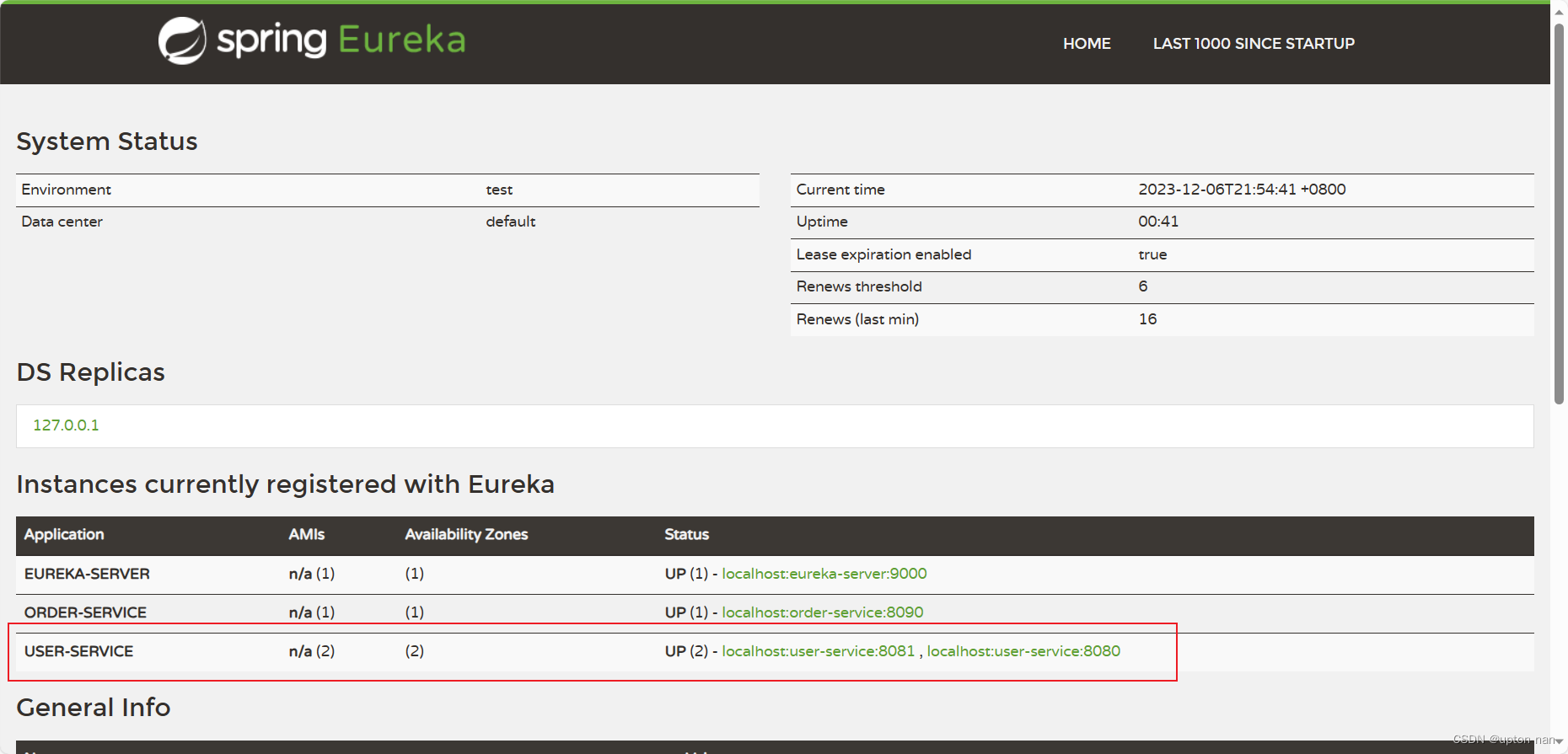
如何从eureka-server上进行服务发现,负载均衡远程调用服务
在spring cloud的maven的pom文件中添加eureka-client的依赖坐标 <!--eureka-client依赖--><dependency><groupId>org.springframework.cloud</groupId><artifactId>spring-cloud-starter-netflix-eureka-client</artifactId></dependen…...

Flutter实现Android拖动到垃圾桶删除效果-Draggable和DragTarget的详细讲解
文章目录 Draggable介绍构造函数参数说明使用示例 DragTarget 介绍构造函数参数说明使用示例 DragTarget 如何接收Draggable传递过来的数据? Draggable介绍 Draggable是Flutter框架中的一个小部件,用于支持用户通过手势拖动一个子部件。它是基于手势的一…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...
