【算法每日一练]-动态规划(保姆级教程 篇13)POJ2686马车旅行 #POJ3254 玉米田 #POJ1185:炮兵阵地
目录
今天知识点
dp每个票的使用情况,然后更新此票状态下的最优解,dp到没有票就行了
dp每行的种植状态,从i-1行进行不断转移
dp每行的种植状态,从i-1和i-2行进行不断转移
POJ2686马车旅行
思路:
POJ3254 玉米田
思路:
POJ1185:炮兵阵地
思路:
前置知识:
基于状态压缩下的集合操作:
1.空集: 0
2.只含有第i个元素的集合{i}: 1<<i
3.含有全部n个元素的集合{0,1,2,....,n-1}: (1<<n)-1
4.判断第i个元素是否属于集合S: if(S>>i&1)
5.向集合中加入第i个元素S ∪ {i}: S|1<<i
6.从集合中除去第i个元素S - {i}: S&~(1<<i)
7.集合S和T的并集S∪T: S | T
8.集合S和T的交集S∩T: S & T
POJ2686马车旅行
有一个公路网连接这些城市,可以乘坐马车通行。乘坐马车需要一张票,旅行者有许多车票,每张票上都标记了马的数量,马越多跑的越快。
你应该考虑如果使用这些票使得在最短时间内把旅行者从出发点他带到目的地的最佳路线。
假设一下条件:
1.通过公路直接连接的两个城市之间只能使用一张车票,且每张票只能用一次
2.乘马车的时间等于两城市之间的距离除以马的数量
3.忽略换乘所需的时间
输入:
2 4 4 2 1
3 1
2 3 3
1 3 3
4 1 2
4 2 5
2 4 3 4 1
5 5
1 2 10
2 3 10
3 4 10
输出:
3.667
impossible
思路:
因为每跑一次票的状态就变动一次,所以我们设置dp[s][u]表示达到当前u点且持有s车票的最小花费,其中s是票的二进制状态。
状态转移:从u到v,当前点v的状态s一定最小的dp[s'][u]+dis/t转移过来(其中s=s'&~(1<<i))
dp[s&~(1<<i)][v]=min(dp[s&~(1<<i)][v],dp[s][u]+dis[u][v]/t[i])
转移顺序:s从大到小,因为大的状态必须要先于小的先确定下来,所以s一定在最外层。然后是每个起点到每个终点使用每张票来去更新每个点,也就是维护该状态下的最优解
#include <bits/stdc++.h>
using namespace std;
const double inf=0x3f3f3f3f;
double ans;
int n,m,p,a,b;
int t[20],dis[50][50];
double dp[1<<10][32];//dp[s][u]表示达到当前u点且持有s车票的最小花费void solve(){for(int i=0;i<(1<<(n+1));i++)for(int j=0;j<=m+1;j++)dp[i][j]=inf;dp[(1<<n)-1][a]=0;//起点状态ans=inf;for(int s=(1<<n)-1;s>=0;s--){//状态从大到小for(int u=1;u<=m;u++)//遍历每个城市for(int i=0;i<n;i++)//遍历每种车票可用就用if((s>>i)&1)for(int v=1;v<=m;v++)//尾点城市if(dis[u][v]>=0){//如果能走,就把第i张票置零dp[s&~(1<<i)][v]=min(dp[s&~(1<<i)][v],dp[s][u]+(double)dis[u][v]/t[i]);}ans=min(ans,dp[s][b]);}}
int main(){while(cin>>n>>m>>p>>a>>b){if(n+m+p+a+b==0)break;for(int i=0;i<n;i++){scanf("%d",&t[i]);//每张车票的数量}memset(dis,-1,sizeof(dis));//初始化成无穷大也行for(int i=0;i<p;i++){//p条变int u,v,w;scanf("%d%d%d",&u,&v,&w);dis[u][v]=dis[v][u]=w;}solve();if(ans==inf)printf("Impossible\n");else printf("%.3lf\n",ans);}
}
POJ3254 玉米田
由m*n(m<12,n<12)的方格组成的玉米田,要在这些方格上种上玉米,有些方格是贫瘠的(0表示),有些是肥沃的(1表示),贫瘠的不能种植。
另外在种植的时候不能在相邻的方格种上玉米,也就是不能共享边。问一共有多少种种植方案。
输入
2 3
1 1 1
0 1 0
思路:
每一行的状态都和上一行的状态有关,状态数有太多因此需要进行状态压缩
首先将每行的状态压缩成j的二进制状态。然后我们进行dp行,设置dp[i][j]表示第i行的第j种状态时对应的前i行的方案数。
转移方程:dp[i][j]=(dp[i][j]+dp[i-1][k])%mod; (k是第i-1行所有的可行状态)
在确定每行转移的时候都要考虑:
1.横向方案 2.横向方案是否和地图匹配 3.是否和i-1行冲突
存每行的可能状态:相邻的两列不能都是1,那就看x&x<<1是不是0(就是可能的横向方案)
是否和i-1冲突:种表示1,不种表示0 那么在判断两行合法性时,不能出现有一列同1(两行都种),所以x&y=0是合法的
存图:肥沃我们用0表示,贫瘠用1表示 那么判断此地和此种法合法性时,不能出现同1(在贫瘠的地方种),所以x&y=0是合法的
(如果不这样的话0和1与是0,你就分不清了)
【注意】:外面每行i循环一次,其次里面是第i行的每个状态j循环一次(找到合适的j),最后是第i-1行的每个状态k循环一次(找到每个合适的k),共O(n^3)
#include <bits/stdc++.h>
using namespace std;
const int mod=1e8;
int sta[600],top,n,m;
int dp[20][600],cur[20];bool check(int x){if(x&x<<1)return 0;return 1;
} void init(){//预处理top=0;for(int i=0;i<(1<<n);i++){//记录所有的没有相邻1的种法if(check(i))sta[++top]=i;}
}void solve(){for(int j=1;j<=top;j++){//处理第一行if(!(sta[j]&cur[1])) dp[1][j]=1;}for(int i=2;i<=m;i++){//处理剩余行for(int j=1;j<=top;j++){//sta[j]是第i行的每种种法if(sta[j]&cur[i]) continue;//检测当前状态是否和当前行匹配for(int k=1;k<=top;k++){//sta[k]是i-1行的每种法if(sta[k]&cur[i-1])continue;//检测当前状态和当前行是否匹配if(sta[j]&sta[k])continue;//第i行和第i-1行有冲突dp[i][j]=(dp[i][j]+dp[i-1][k])%mod;}}}
}int main(){while(cin>>m>>n){//m是行n是列init();int num;memset(dp,0,sizeof(dp));for(int i=1;i<=m;i++){cur[i]=0;for(int j=1;j<=n;j++){scanf("%d",&num);if(num==0)cur[i]+=(1<<(n-j));//读入地图 1变0,0变1}}solve();int ans=0;for(int j=1;j<=top;j++)ans=(ans+dp[m][j])%mod;//最后一行所有方案数加起来cout<<ans;}
}
POJ1185:炮兵阵地
在N*M(N<100,M<10)的地图上布置炮兵,H格子为山地不能布置,P格子为平原可以布置。炮兵的攻击范围是沿横向左右各两格,沿纵向上下个两格子
炮兵之间不能误伤。问在整个地图中最多能拜访多少个炮兵?
5 4
PHPP
PPHH
PPPP
PHPP
PHHP
思路:
首先要对行进行状态压缩(对列的话太大了,枚举2^100还不如不压缩呢),我们每次确定行的状态都需要考虑:
1.横向方案 2.横向方案是否和地图匹配 3.是否和i-1行i-2行冲突
设置dp[i][j][k]表示第i行为第j状态,第i-1行为第k状态时 对应的前i行放置的最大炮兵数。
转移方程:dp[i][j][k]=max(dp[i][j][k],dp[i-1][k][t]+num[j]);
(j是第i行的方案,k是第i-1行的方案,t是i-2行的方案)
存每行的可能状态:左右相邻1个间隔和2个间隔都不能炮兵(就是可能的横向方案)
存图:(1,1)开始存。0表示平原,1表示山地,那么在放置的时候不能出现同1(在山地放炮兵),所以x&y=0是合法的(保证合法的是0就行了)
是否冲突:第i行和第i-1行,第i-2行 不能出现有一列同1(两行都放炮兵),所以x&y=0是合法的
【注意】:外面每行i循环一次,其次里面是第i行的每个状态j循环一次(找到合适的j),然后是第i-1行的每个状态k循环一次(供第i行找到合适的k),
接着是第i-2行的每个状态t循环一次(供第i-1行找到合适的t)
#include <bits/stdc++.h>
using namespace std;
int n,m,top;
char mp[110][20];
int num[70];
int stk[70],cur[70];//stk表示横向可能的方案,cur是我们存的地图行
int dp[110][70][70];bool check(int x){if(x&(x<<1))return 0;//相邻1间隔是否合法if(x&(x<<2))return 0;//相邻2间隔是否合法return 1;
}void init(){//统计所有的可能合法状态,最多60种top=0;for(int i=0;i<(1<<m);i++){if(check(i))stk[top++]=i;}
}int count(int x){//统计x二进制中1的个数int cnt=0;while(x){if(x&1)cnt++;x=x>>1;}
// while(x){//这个更快
// cnt++;
// x&=(x-1);
// } return cnt;
}int solve(){int ans=0;memset(dp,-1,sizeof(dp));for(int j=0;j<top;j++){//初始化第一行的状态num[j]=count(stk[j]);if(!(stk[j]&cur[1])){//和地图匹配dp[1][j][0]=num[j];//第一行状态为j,上一行状态为0(知道为啥从(1,1)开始初始化了把)ans=max(ans,dp[1][j][0]);}}for(int i=2;i<=n;i++){//处理每一行for(int j=0;j<top;j++){//遍历第i行的可能方案if(stk[j]&cur[i])continue;//是否和地图匹配for(int k=0;k<top;k++){//遍历第i-1行的可能方案if(stk[j]&stk[k])continue;//此行和上一行是否匹配(不用再判断和地图是否匹配,不匹配dp是-1,不影响的)for(int t=0;t<top;t++){//遍历上二行可能方案if(stk[j]&stk[t])continue;//此行和上二行是否匹配dp[i][j][k]=max(dp[i][j][k],dp[i-1][k][t]+num[j]);}if(i==n)ans=max(ans,dp[i][j][k]);//不要放在外面套3个for取max}}}return ans;
}
int main(){while(cin>>n>>m){init();for(int i=1;i<=n;i++){scanf("%s",mp[i]+1);//加1是为了从1下标开始存}for(int i=1;i<=n;i++){cur[i]=0;for(int j=1;j<=m;j++){if(mp[i][j]=='H')//同样的,不能放的地方存1cur[i]+=(1<<(m-j));}}cout<<solve();}
}
相关文章:
POJ2686马车旅行 #POJ3254 玉米田 #POJ1185:炮兵阵地)
【算法每日一练]-动态规划(保姆级教程 篇13)POJ2686马车旅行 #POJ3254 玉米田 #POJ1185:炮兵阵地
目录 今天知识点 dp每个票的使用情况,然后更新此票状态下的最优解,dp到没有票就行了 dp每行的种植状态,从i-1行进行不断转移 dp每行的种植状态,从i-1和i-2行进行不断转移 POJ2686马车旅行 思路: POJ3254 玉米田…...

工业固体废物智能化综合管控平台
工业固体废物智能化综合管控平台,涵盖产废企业、运输企业、固废处置企 业等不同群体应用,根据不同群体设计不同的业务应用子系统功能,以及各个不 同群体的环保物联网平台子系统功能模块,同时具有移动端的应用APP。 建立产废企业端…...
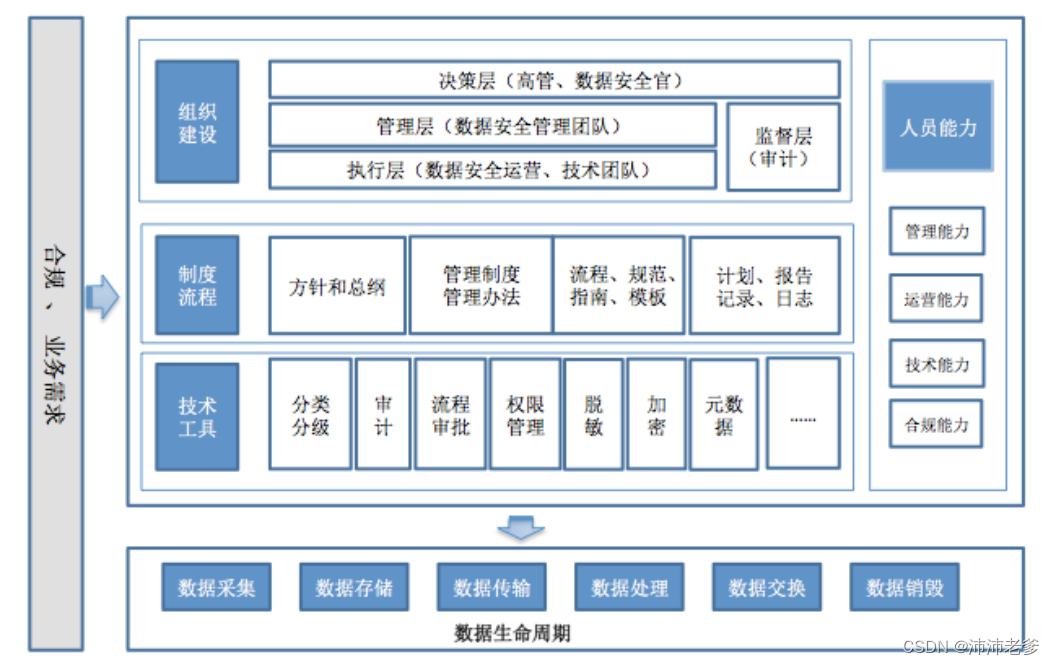
玩转大数据12:大数据安全与隐私保护策略
1. 引言 大数据的快速发展,为各行各业带来了巨大的变革,也带来了新的安全和隐私挑战。大数据系统通常处理大量敏感数据,包括个人身份信息、财务信息、健康信息等。如果这些数据被泄露或滥用,可能会对个人、企业和社会造成严重的损…...

Qt工程文件分离、Qtimer定时器、Qt Creator 常用快捷键
Qt 工程文件分离 不含 UI 的文件分离 以堆栈窗体的代码为例。 firstpagewidget.h #ifndef FIRSTPAGEWIDGET_H #define FIRSTPAGEWIDGET_H#include <QtWidgets> // 记得修改class firstPageWidget : public QWidget {Q_OBJECT public:explicit firstPageWidget(QW…...

验收支撑-软件项目验收计划书
软件项目验收计划的作用主要有以下几点: 确保项目质量:通过项目验收,客户或相关方可以对项目的成果进行全面、系统的评估,以确保项目达到预期的质量标准。发现和解决问题:在项目开发过程中,难免会存在一些问…...

SQL注入绕过技术
预计更新SQL注入概述 1.1 SQL注入攻击概述 1.2 SQL注入漏洞分类 1.3 SQL注入攻击的危害 SQLMap介绍 2.1 SQLMap简介 2.2 SQLMap安装与配置 2.3 SQLMap基本用法 SQLMap进阶使用 3.1 SQLMap高级用法 3.2 SQLMap配置文件详解 3.3 SQLMap插件的使用 SQL注入漏洞检测 4.1 SQL注入…...

锂电池基础知识及管理方式总结
这两天在排查一个锂电池无法充电的问题,用的是电池管理芯片BQ25713,网上相关的资料也很少,查看数据手册时,里面也有很多术语参数等不是很理解,所以,在此对锂电池的基础知识做个简单的总结,方面后…...

小红书基于零信任 SASE 办公安全解决方案,斩获 “IDC 中国 20 大杰出安全项目”
近日,由 IDC 主办的 2023 全球 CSO 网络安全峰会(中国站)在京举行,峰会荟萃 300 生态伙伴和行业领袖,共同探讨新形势下的数据安全保护,畅议未来网络安全的可靠航道。 会上,“2023 IDC 中国20大杰…...

html通过CDN引入Vue使用Vuex以及Computed、Watch监听
html通过CDN引入Vue使用Vuex以及Computed、Watch监听 近期遇到个需求,就是需要在.net MVC的项目中,对已有的项目的首页进行优化,也就是写原生html和js。但是咱是一个写前端的,写html还可以,.net的话,开发也…...

【LabVIEW学习】5.数据通信之TCP协议,控制电脑的一种方式
一。tcp连接以及写数据(登录) 数据通信--》协议--》TCP 1.tcp连接 创建while循环,中间加入事件结构,创建tcp连接,写入IP地址与端口号 2.写入tcp数据 登录服务器除了要知道IP地址以及端口以外,需要用户名与密…...
uview1 的u-tabs组件在微信小程序中会出现横向滚动条
uview1 的u-tabs组件在微信小程序中会出现横向滚动条,真机才会生效,微信开发者工具没问题包括官方示例也会 原因:未屏蔽微信小程序的滚动条 解决办法:uview-ui中uview-ui/components/u-tabs/u-tabs.vue文件把h5屏蔽滚动条的条件编…...

服务器ipv6地址显示“scope global dadfailed tentative noprefixroute”无法连通的问题处理一例
服务器规模启用ipv6地址后,遇到一起案例 ,配置的服务ipv6地址显示“scope global dadfailed tentative noprefixroute”,无法连通,现将解决过程记录如下。 一、问题情况 1、ipv6信息检查 某台服务器配置ipv6地址后,…...
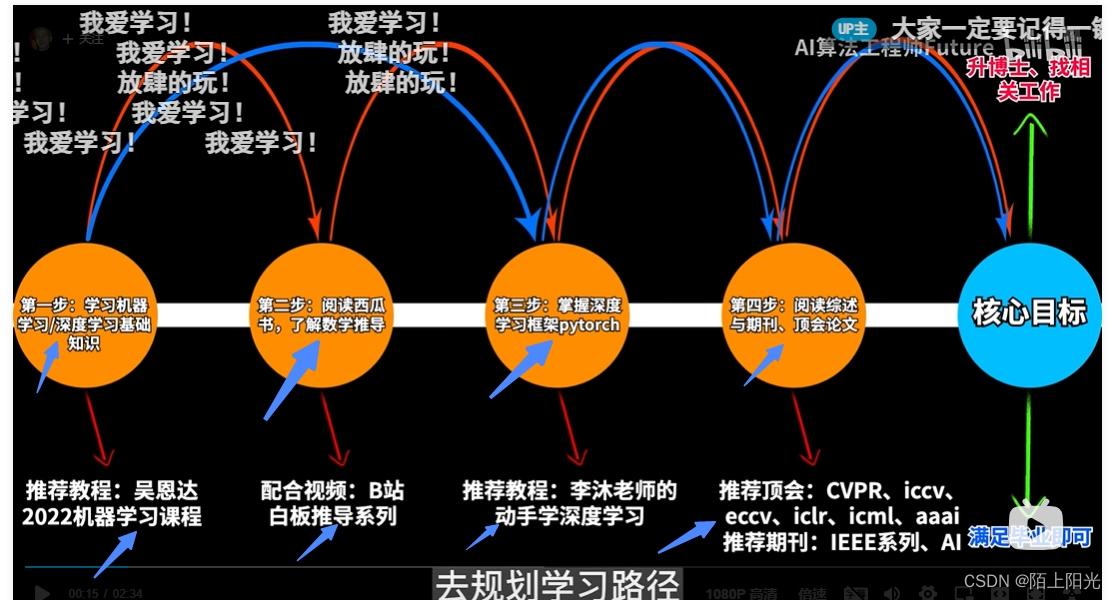
深度学习学习顺序梳理
https://www.bilibili.com/video/BV1to4y1G7xq/?spm_id_from333.999.0.0&vd_source9607a6d9d829b667f8f0ccaaaa142fcb 1.吴恩达机器学习课程 已学完,时间较久了,后续可以重新听一遍,整理一下笔记 2. 白板推导读西瓜书 统计学习方法看…...

机器学习实验六:聚类
系列文章目录 机器学习实验一:线性回归机器学习实验二:决策树模型机器学习实验三:支持向量机模型机器学习实验四:贝叶斯分类器机器学习实验五:集成学习机器学习实验六:聚类 文章目录 系列文章目录一、实验…...

逆向思考 C. Fence Painting
Problem - 1481C - Codeforces 思路:逆序考虑,因为每一块木板都是被最后一次粉刷所决定的。 从后往前开始,对于 c i c_i ci来说, 如果这个颜色还有没有涂的木板,那么涂到其中一个木板即可如果这个颜色下没有未涂的…...

当当狸AR智能学习图集跨越千年文明传承,邀您“面对面”与虚拟诗人互动对诗
中华传统文化底蕴深厚,余韵悠长。即使经过千年的历史裂变,依然历久铭心慰藉着一代又一代人的灵魂。千百年后的今天,成为了我们独一无二的财富。 如今,国人学习中华传统文化的方式有很多,诗词集、动画影片、诗歌传颂等…...

CESM笔记——component活动状态+compset前缀解析+B1850,BHIST区别
时隔一年没写CSDN笔记了,一些CESM的知识点我都快忘了。诶,主要是在国外办公室的网屏蔽了好多国内的网络,CSDN登不上,回家又不想干活。。。好吧,好多借口。。。 昨天师弟问我一些问题,想想要不可以水一篇小…...

vue 页面跳转时,浏览器上方显示进度条
vue 页面跳转时,浏览器上方显示进度条 文章目录 vue 页面跳转时,浏览器上方显示进度条先看效果一、安装 nprogress二、main.js 引入nprogress1.引入库 三、在router.js中对路由钩子进行设置四、测试 先看效果 vue 页面跳转时,浏览器上方显示进…...

tqdm输出字符串被截断
tqdm输出截断 1.遇到的问题2.tqdm默认的字符串长度是80(ncols属性)3.修改tqdm的ncols属性4.本人字符串长度是64 1.遇到的问题 字符串打印,显示不完整, 2.tqdm默认的字符串长度是80(ncols属性) 3.修改tqdm的…...
Qt::UniqueConnection和lambda一块用无效
如果槽函数是lambda。 那么用了Qt::UniqueConnection也会出现槽函数被多次调用的问题。 原因: 参考官方文档: QObject Class | Qt Core 5.15.16https://doc.qt.io/qt-5/qobject.html#connect...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

Webpack性能优化:构建速度与体积优化策略
一、构建速度优化 1、升级Webpack和Node.js 优化效果:Webpack 4比Webpack 3构建时间降低60%-98%。原因: V8引擎优化(for of替代forEach、Map/Set替代Object)。默认使用更快的md4哈希算法。AST直接从Loa…...

根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的----NTFS源代码分析--重要
根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的 第一部分: 0: kd> g Breakpoint 9 hit Ntfs!ReadIndexBuffer: f7173886 55 push ebp 0: kd> kc # 00 Ntfs!ReadIndexBuffer 01 Ntfs!FindFirstIndexEntry 02 Ntfs!NtfsUpda…...
