Python 全栈体系【四阶】(五)
第四章 机器学习
三、数据预处理
1. 数据预处理的目的
去除无效数据、不规范数据、错误数据
补齐缺失值
对数据范围、量纲、格式、类型进行统一化处理,更容易进行后续计算
2. 预处理方法
2.1 标准化(均值移除)
让样本矩阵中的每一列的平均值为 0,标准差为 1。如有三个数 a, b, c,则平均值为:
m = ( a + b + c ) / 3 a ′ = a − m b ′ = b − m c ′ = c − m m = (a + b + c) / 3 \\ a' = a - m \\ b' = b - m \\ c' = c - m m=(a+b+c)/3a′=a−mb′=b−mc′=c−m
预处理后的平均值为 0:
( a ′ + b ′ + c ′ ) / 3 = ( ( a + b + c ) − 3 m ) / 3 = 0 (a' + b' + c') / 3 =( (a + b + c) - 3m) / 3 = 0 (a′+b′+c′)/3=((a+b+c)−3m)/3=0
预处理后的标准差:
s = s q r t ( ( ( a − m ) 2 + ( b − m ) 2 + ( c − m ) 2 ) / 3 ) s = sqrt(((a - m)^2 + (b - m)^2 + (c - m)^2)/3) s=sqrt(((a−m)2+(b−m)2+(c−m)2)/3)
a ′ ′ = a / s a'' = a / s a′′=a/s
b ′ ′ = b / s b'' = b / s b′′=b/s
c ′ ′ = c / s c'' = c / s c′′=c/s
s ′ ′ = s q r t ( ( ( a ′ / s ) 2 + ( b ′ / s ) 2 + ( c ′ / s ) 2 ) / 3 ) s'' = sqrt(((a' / s)^2 + (b' / s) ^ 2 + (c' / s) ^ 2) / 3) s′′=sqrt(((a′/s)2+(b′/s)2+(c′/s)2)/3)
= s q r t ( ( a ′ 2 + b ′ 2 + c ′ 2 ) / ( 3 ∗ s 2 ) ) =sqrt((a'^2 + b'^2 + c'^2) / (3 *s ^2)) =sqrt((a′2+b′2+c′2)/(3∗s2))
= 1 =1 =1
标准差:又称均方差,是离均差平方的算术平均数的平方根,用 σ 表示 ,标准差能反映一个数据集的离散程度。
代码示例:
# 数据预处理之:均值移除示例
import numpy as np
import sklearn.preprocessing as sp# 样本数据
raw_samples = np.array([[3.0, -1.0, 2.0],[0.0, 4.0, 3.0],[1.0, -4.0, 2.0]
])
print(raw_samples)
print(raw_samples.mean(axis=0)) # 求每列的平均值
print(raw_samples.std(axis=0)) # 求每列标准差std_samples = raw_samples.copy() # 复制样本数据
for col in std_samples.T: # 遍历每列col_mean = col.mean() # 计算平均数col_std = col.std() # 求标准差col -= col_mean # 减平均值col /= col_std # 除标准差print(std_samples)
print(std_samples.mean(axis=0))
print(std_samples.std(axis=0))
"""
[[ 3. -1. 2.][ 0. 4. 3.][ 1. -4. 2.]]
[ 1.33333333 -0.33333333 2.33333333]
[1.24721913 3.29983165 0.47140452]
[[ 1.33630621 -0.20203051 -0.70710678][-1.06904497 1.31319831 1.41421356][-0.26726124 -1.1111678 -0.70710678]]
[ 5.55111512e-17 0.00000000e+00 -2.96059473e-16]
[1. 1. 1.]
"""
也可以通过 sklearn 提供 sp.scale 函数实现同样的功能,如下面代码所示:
std_samples = sp.scale(raw_samples) # 求标准移除
print(std_samples)
print(std_samples.mean(axis=0))
print(std_samples.std(axis=0))
"""
[[ 1.33630621 -0.20203051 -0.70710678][-1.06904497 1.31319831 1.41421356][-0.26726124 -1.1111678 -0.70710678]]
[ 5.55111512e-17 0.00000000e+00 -2.96059473e-16]
[1. 1. 1.]
"""
2.2 范围缩放
将样本矩阵中的每一列最小值和最大值设定为相同的区间,统一各特征值的范围.如有 a, b, c 三个数,其中 b 为最小值,c 为最大值,则:
a ′ = a − b a' = a - b a′=a−b
b ′ = b − b b' = b - b b′=b−b
c ′ = c − b c' = c - b c′=c−b
缩放计算方式如下公式所示:
a ′ ′ = a ′ / c ′ a'' = a' / c' a′′=a′/c′
b ′ ′ = b ′ / c ′ b'' = b' / c' b′′=b′/c′
c ′ ′ = c ′ / c ′ c'' = c' / c' c′′=c′/c′
计算完成后,最小值为 0,最大值为 1。以下是一个范围缩放的示例。
# 数据预处理之:范围缩放
import numpy as np
import sklearn.preprocessing as sp# 样本数据
raw_samples = np.array([[1.0, 2.0, 3.0],[4.0, 5.0, 6.0],[7.0, 8.0, 9.0]]).astype("float64")# print(raw_samples)
mms_samples = raw_samples.copy() # 复制样本数据for col in mms_samples.T:col_min = col.min()col_max = col.max()col -= col_mincol /= (col_max - col_min)
print(mms_samples)"""
[[0. 0. 0. ][0.5 0.5 0.5][1. 1. 1. ]]
"""
也可以通过 sklearn 提供的对象实现同样的功能,如下面代码所示:
# 根据给定范围创建一个范围缩放器对象
mms = sp.MinMaxScaler(feature_range=(0, 1))# 定义对象(修改范围观察现象)
# 使用范围缩放器实现特征值范围缩放
mms_samples = mms.fit_transform(raw_samples) # 缩放
print(mms_samples)
"""
[[0. 0. 0. ][0.5 0.5 0.5][1. 1. 1. ]]
"""
执行结果:
[[0. 0. 0. ][0.5 0.5 0.5][1. 1. 1. ]]
[[0. 0. 0. ][0.5 0.5 0.5][1. 1. 1. ]]
3. 归一化 Normalize
反映样本所占比率。
用每个样本的每个特征值,除以该样本各个特征值绝对值之和。
变换后的样本矩阵,每个样本的特征值绝对值之和为 1。
例如如下反映编程语言热度的样本中,2018 年也 2017 年比较,Python 开发人员数量减少了 2 万,但是所占比率确上升了:
| 年份 | Python(万人) | Java(万人) | PHP(万人) |
|---|---|---|---|
| 2017 | 10 | 20 | 5 |
| 2018 | 8 | 10 | 1 |
归一化预处理示例代码如下所示:
# 数据预处理之:归一化
import numpy as np
import sklearn.preprocessing as sp# 样本数据
raw_samples = np.array([[10.0, 20.0, 5.0],[8.0, 10.0, 1.0]
])
print(raw_samples)
nor_samples = raw_samples.copy() # 复制样本数据for row in nor_samples:row /= abs(row).sum() # 先对行求绝对值,再求和,再除以绝对值之和print(nor_samples) # 打印结果
"""
[[10. 20. 5.][ 8. 10. 1.]]
[[0.28571429 0.57142857 0.14285714][0.42105263 0.52631579 0.05263158]]
"""
在 sklearn 库中,可以调用 sp.normalize()函数进行归一化处理,函数原型为:
sp.normalize(原始样本, norm='l2')
# l1: l1范数,除以向量中各元素绝对值之和
# l2: l2范数,除以向量中各元素平方之和
使用 sklearn 库中归一化处理代码如下所指示:
nor_samples = sp.normalize(raw_samples, norm='l1')
print(nor_samples) # 打印结果
"""
[[0.28571429 0.57142857 0.14285714][0.42105263 0.52631579 0.05263158]]
"""
4. 二值化
根据一个事先给定的阈值,用 0 和 1 来表示特征值是否超过阈值.以下是实现二值化预处理的代码:
# 二值化
import numpy as np
import sklearn.preprocessing as spraw_samples = np.array([[65.5, 89.0, 73.0],[55.0, 99.0, 98.5],[45.0, 22.5, 60.0]])
bin_samples = raw_samples.copy() # 复制数组
# 生成掩码数组
mask1 = bin_samples < 60
mask2 = bin_samples >= 60
# 通过掩码进行二值化处理
bin_samples[mask1] = 0
bin_samples[mask2] = 1print(bin_samples) # 打印结果
"""
[[1. 1. 1.][0. 1. 1.][0. 0. 1.]]
"""
同样,也可以利用 sklearn 库来处理:
bin = sp.Binarizer(threshold=59) # 创建二值化对象(注意边界值)
bin_samples = bin.transform(raw_samples) # 二值化预处理
print(bin_samples)
"""
[[1. 1. 1.][0. 1. 1.][0. 0. 1.]]
"""
二值化编码会导致信息损失,是不可逆的数值转换。如果进行可逆转换,则需要用到独热编码。
5. 独热编码
根据一个特征中不重复值的个数来建立一个由一个 1 和若干个 0 组成的序列,用来序列对所有的特征值进行编码。例如有如下样本:
[ 1 3 2 7 5 4 1 8 6 7 3 9 ] \left[ \begin{matrix} 1 & 3 & 2\\ 7 & 5 & 4\\ 1 & 8 & 6\\ 7 & 3 & 9\\ \end{matrix} \right] 171735832469
对于第一列,有两个值,1 使用 10 编码,7 使用 01 编码
对于第二列,有三个值,3 使用 100 编码,5 使用 010 编码,8 使用 001 编码
对于第三列,有四个值,2 使用 1000 编码,4 使用 0100 编码,6 使用 0010 编码,9 使用 0001 编码
编码字段,根据特征值的个数来进行编码,通过位置加以区分.通过独热编码后的结果为:
[ 10 100 1000 01 010 0100 10 001 0010 01 100 001 ] \left[ \begin{matrix} 10 & 100 & 1000\\ 01 & 010 & 0100\\ 10 & 001 & 0010\\ 01 & 100 & 001\\ \end{matrix} \right] 10011001100010001100100001000010001
使用 sklearn 库提供的功能进行独热编码的代码如下所示:
# 独热编码示例
import numpy as np
import sklearn.preprocessing as spraw_samples = np.array([[1, 3, 2],[7, 5, 4],[1, 8, 6],[7, 3, 9]])one_hot_encoder = sp.OneHotEncoder(sparse=False, # 是否采用稀疏格式dtype="int32",categories="auto")# 自动编码
oh_samples = one_hot_encoder.fit_transform(raw_samples) # 执行独热编码
print(oh_samples)print(one_hot_encoder.inverse_transform(oh_samples)) # 解码
执行结果:
[[1 0 1 0 0 1 0 0 0][0 1 0 1 0 0 1 0 0][1 0 0 0 1 0 0 1 0][0 1 1 0 0 0 0 0 1]][[1 3 2][7 5 4][1 8 6][7 3 9]]
6. 标签编码
根据字符串形式的特征值在特征序列中的位置,来为其指定一个数字标签,用于提供给基于数值算法的学习模型。
代码如下所示:
# 标签编码
import numpy as np
import sklearn.preprocessing as spraw_samples = np.array(['audi', 'ford', 'audi','bmw','ford', 'bmw'])lb_encoder = sp.LabelEncoder() # 定义标签编码对象
lb_samples = lb_encoder.fit_transform(raw_samples) # 执行标签编码
print(lb_samples)print(lb_encoder.inverse_transform(lb_samples)) # 逆向转换
执行结果:
[0 2 0 1 2 1]
['audi' 'ford' 'audi' 'bmw' 'ford' 'bmw']
四、练习
1. 判断以下哪个是回归问题,哪个是分类问题,哪个是聚类问题。
-
判断一封邮件是否为垃圾邮件(分类)
-
在图像上检测出人脸的位置(回归,预测 x,y,w,h 四个值,每个值都是连续的)
-
视频网站根据用户观看记录,找出喜欢看战争电影的用户(聚类)
2. 分类和聚类主要区别是什么?
- 分类是有监督学习,聚类是无监督学习
3. 判断以下哪些是数据降维问题
- 将 8*8 的矩阵缩小为 4*4 的矩阵(是)
- 将二维矩阵变形为一维向量(是)
- 将高次方程模型转换为低次方程模型(是)
相关文章:
)
Python 全栈体系【四阶】(五)
第四章 机器学习 三、数据预处理 1. 数据预处理的目的 去除无效数据、不规范数据、错误数据 补齐缺失值 对数据范围、量纲、格式、类型进行统一化处理,更容易进行后续计算 2. 预处理方法 2.1 标准化(均值移除) 让样本矩阵中的每一列的…...

原点处可微问题
文章目录 原点可微问题例例 原点可微问题 lim x → 0 , y → 0 f ( x , y ) − f ( 0 , 0 ) x 2 y 2 \lim\limits_{x\to{0},y\to{0}} \frac{f(x,y)-f(0,0)}{\sqrt{x^2y^2}} x→0,y→0limx2y2 f(x,y)−f(0,0) 0 0 0(1)是函数 f ( x , y ) f(x,y) f(x,y)在 ( 0 , 0 ) (…...
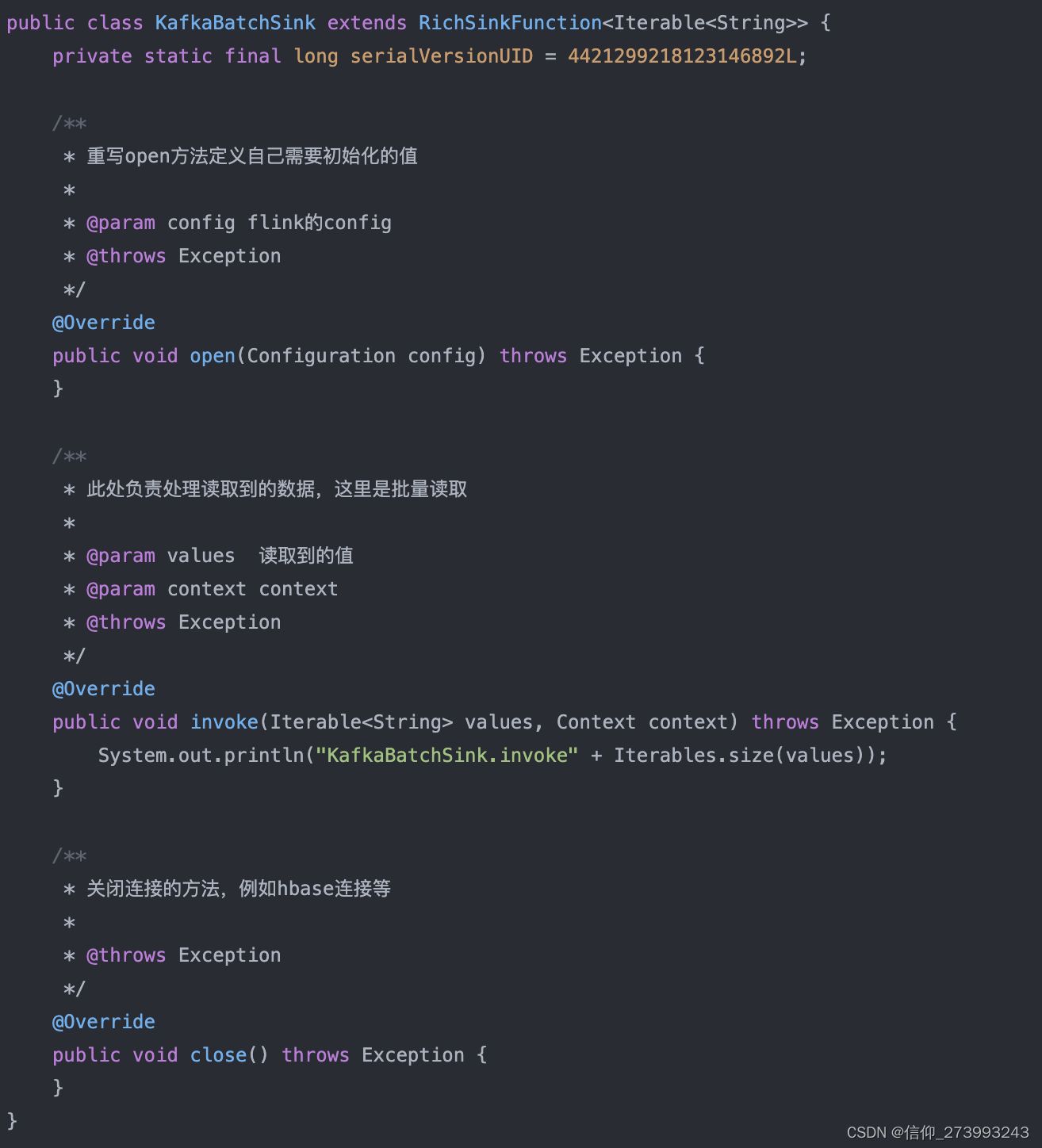
Flink+Kafka消费
引入jar <dependency><groupId>org.apache.flink</groupId><artifactId>flink-java</artifactId><version>1.8.0</version> </dependency> <dependency><groupId>org.apache.flink</groupId><artifactI…...

Seconds_Behind_Master越来越大,主从同步延迟
问题现象 发现从库mysql_slave的参数Seconds_Behind_Master越来越大。已排除主从服务器时间不一致;那么主要就判断两点:是io thread慢还是 sql thread慢?先观察show slave status\G 。 判断3个参数(参数后面的值是默认空闲时候的…...

除法求值[中等]
一、题目 给你一个变量对数组equations和一个实数值数组values作为已知条件,其中equations[i] [Ai, Bi]和values[i]共同表示等式Ai / Bi values[i]。每个Ai或Bi是一个表示单个变量的字符串。另有一些以数组queries表示的问题,其中queries[j] [Cj, Dj…...

新时代商业市场:AR技术的挑战与机遇并存
随着科技的不断发展,增强现实(AR)技术逐渐成为当今社会的一个重要组成部分。AR技术能够将虚拟世界与现实世界相结合,为人们提供更加丰富、多样化的体验。在新时代的社会商业市场中,AR技术也正逐渐被应用于各种商业活动…...

RHEL8中ansible的使用
编写ansible.cfg和清单文件ansible的基本用法 本章实验三台RHEL8系统(rhel801,rhel802,rhel803),其中rhel801是ansible主机 这里要确保ansible主机能够解析所有被管理的机器,这里通过配置/etc/hosts来实现…...

【1.6计算机组成与体系结构】存储系统
目录 1.层次化存储结构2.Cache2.1 Cache的介绍2.2 局部性原理2.3 Cache应用 1.层次化存储结构 由 ⬆ CPU:寄存器。 快 ⬆ Cache:按内容存取(相联存储器)。 到 ⬆内存(主存):DRAM。 慢 ⬆ 外存(辅存&#…...
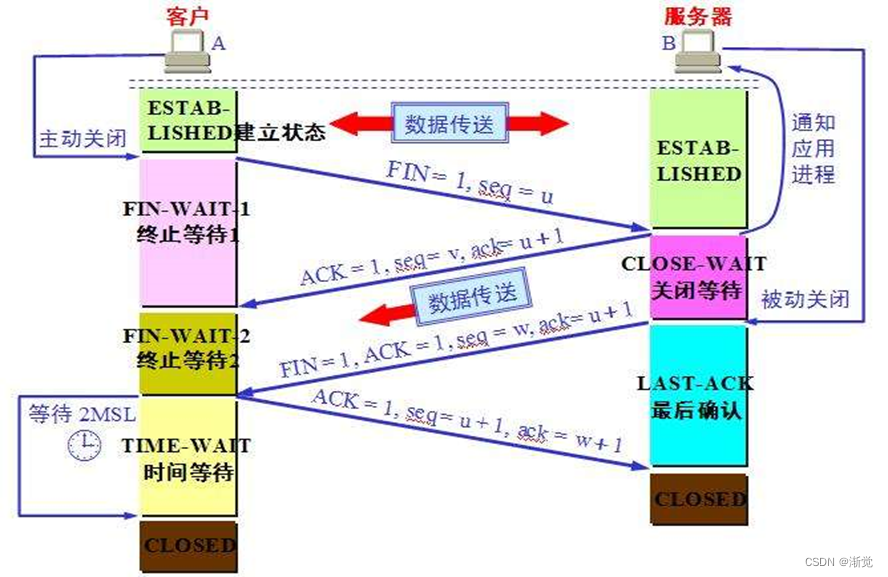
TCP/UDP 协议
目录 一.TCP协议 1.介绍 2.报文格式 编辑 确认号 控制位 窗口大小 3.TCP特性 二.TCP协议的三次握手 1.tcp 三次握手的过程 三.四次挥手 2.有限状态机 四.tcp协议和udp协议的区别 五.udp协议 UDP特性 六.telnet协议 一.TCP协议 1.介绍 TCP(Transm…...

如何正确理解和使用 Golang 中 nil ?
目录 指针中的 nil 切片中的 nil map 中的 nil 通道中的 nil 函数中的 nil 接口中的 nil 避免 nil 相关问题的最佳实践 小结 在 Golang 中,nil 是一个预定义的标识符,在不同的上下文环境中有不同的含义,但通常表示“无”、“空”或“…...
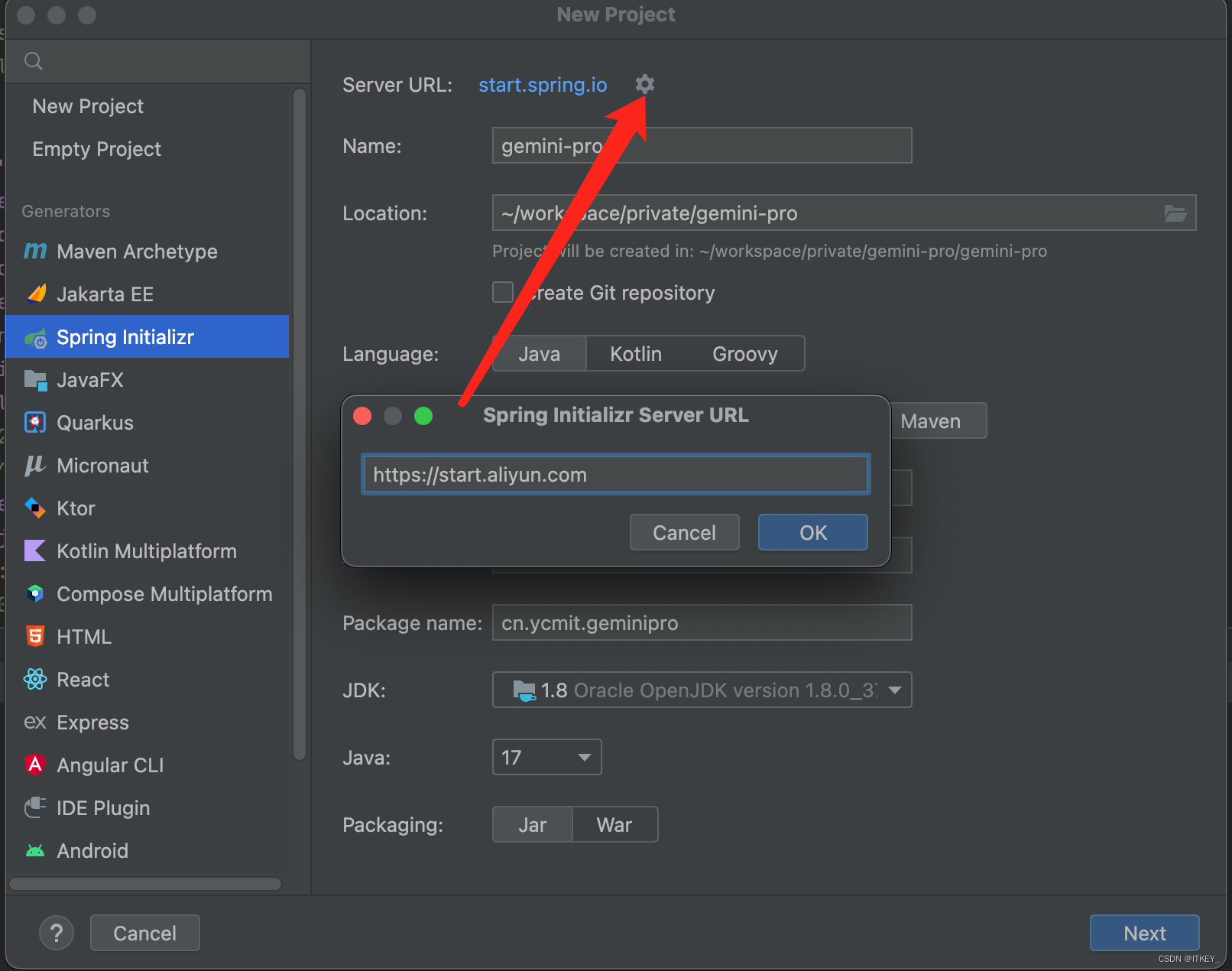
IDEA新建jdk8 spring boot项目
今天新建spring boot项目发现JDK版本最低可选17。 但是目前用的最多的还是JDK8啊。 解决办法 Server URL中设置: https://start.aliyun.com/设置完成后,又可以愉快的用jdk8创建项目了。 参考 https://blog.csdn.net/imbzz/article/details/13469117…...

Qt/C++音视频开发59-使用mdk-sdk组件/原qtav作者力作/性能凶残/超级跨平台
一、前言 最近一个月一直在研究mdk-sdk音视频组件,这个组件是原qtav作者的最新力作,提供了各种各样的示例demo,不仅限于支持C,其他各种比如java/flutter/web/android等全部支持,性能上也是杠杠的,目前大概…...

智安网络|企业网络安全工具对比:云桌面与堡垒机,哪个更适合您的需求
随着云计算技术的快速发展,越来越多的企业开始采用云计算解决方案来提高效率和灵活性。在云计算环境下,云桌面和堡垒机被广泛应用于企业网络安全和办公环境中。尽管它们都有助于提升企业的安全和效率,但云桌面和堡垒机在功能和应用方面存在着…...
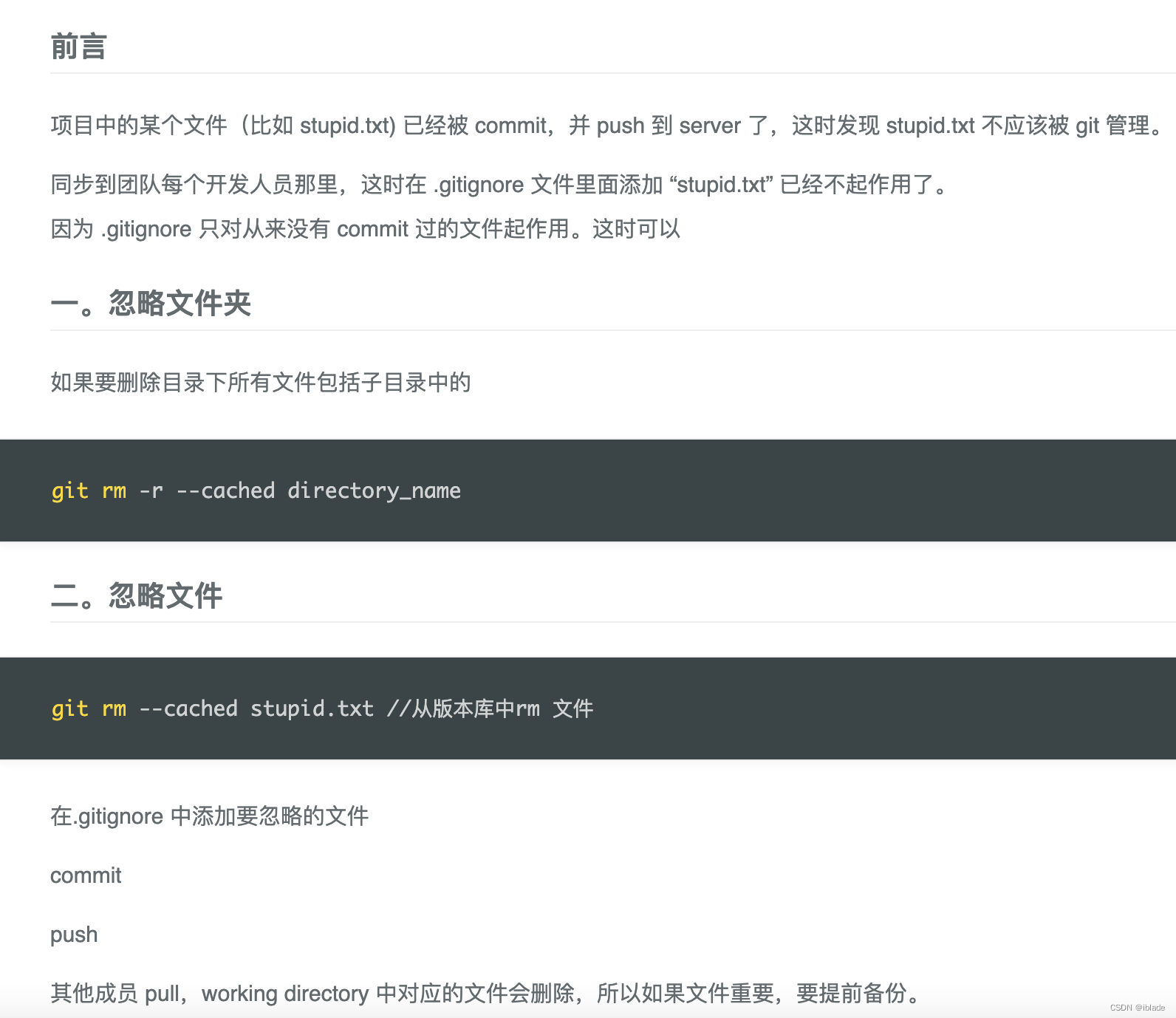
Git忽略已经提交的文件
原理类似于 Android修改submodule的lib包名...

MVVM和MVC以及MVP的原理以及它们的区别
MVVM、MVC 和 MVP 都是前端架构模式,它们各自有不同的原理和特点。 MVC(Model-View-Controller) 原理:MVC 将应用程序分为三个部分:模型(Model)、视图(View)和控制器&a…...
WeChatMsg: 导出微信聊天记录 | 开源日报 No.108
Mozilla-Ocho/llamafile Stars: 3.5k License: NOASSERTION llamafile 是一个开源项目,旨在通过将 lama.cpp 与 Cosmopolitan Libc 结合成一个框架,将 LLM (Large Language Models) 的复杂性折叠到单个文件可执行程序中,并使其能够在大多数…...
)
Python学习之复习MySQL-Day3(DQL)
目录 文章声明⭐⭐⭐让我们开始今天的学习吧!DQL简介基本查询查询多个/全部字段设置别名去除重复记录 条件查询条件查询介绍实例演示 聚合函数什么是聚合函数?常见的聚合函数实例演示 分组查询分组查询语法where 和 having 的区别实例演示 排序查询语法实…...

AI超级个体:ChatGPT与AIGC实战指南
目录 前言 一、ChatGPT在日常工作中的应用场景 1. 客户服务与支持 2. 内部沟通与协作 3. 创新与问题解决 二、巧用ChatGPT提升工作效率 1. 自动化工作流程 2. 信息整合与共享 3. 提高决策效率 三、巧用ChatGPT创造价值 1. 优化产品和服务 2. 提高员工满意度和留任率…...
|(使用OkHttpClient实现websocket以及详细介绍))
SpringBoot集成websocket(5)|(使用OkHttpClient实现websocket以及详细介绍)
SpringBoot集成websocket(5)|(使用OkHttpClient实现websocket以及详细介绍) 文章目录 SpringBoot集成websocket(5)|(使用OkHttpClient实现websocket以及详细介绍)[TOC] 前言一、初始…...
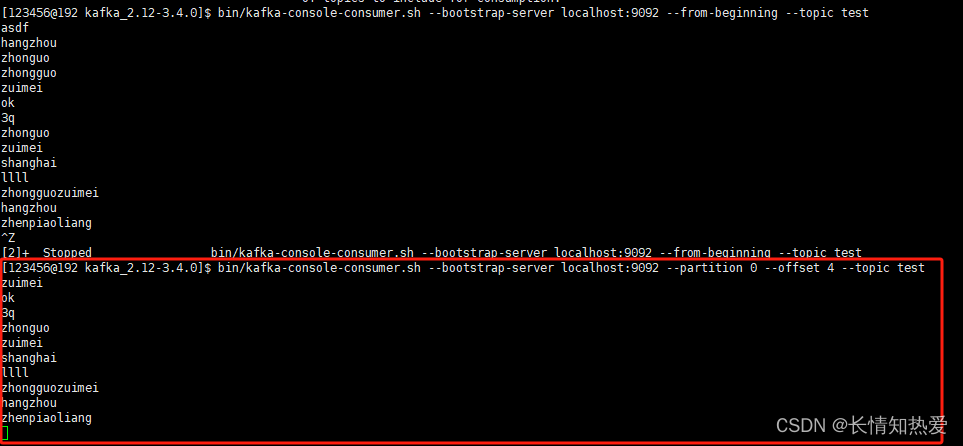
Kafka-Kafka基本原理与集群快速搭建(实践)
Kafka单机搭建 下载Kafka Apache Download Mirrors 解压 tar -zxvf kafka_2.12-3.4.0.tgz -C /usr/local/src/software/kafkakafka内部bin目录下有个内置的zookeeper(用于单机) 启动zookeeper(在后台启动) nohup bin/zookeeper-server-start.sh conf…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

MinIO Docker 部署:仅开放一个端口
MinIO Docker 部署:仅开放一个端口 在实际的服务器部署中,出于安全和管理的考虑,我们可能只能开放一个端口。MinIO 是一个高性能的对象存储服务,支持 Docker 部署,但默认情况下它需要两个端口:一个是 API 端口(用于存储和访问数据),另一个是控制台端口(用于管理界面…...

flow_controllers
关键点: 流控制器类型: 同步(Sync):发布操作会阻塞,直到数据被确认发送。异步(Async):发布操作非阻塞,数据发送由后台线程处理。纯同步(PureSync…...

基于开源AI智能名片链动2 + 1模式S2B2C商城小程序的沉浸式体验营销研究
摘要:在消费市场竞争日益激烈的当下,传统体验营销方式存在诸多局限。本文聚焦开源AI智能名片链动2 1模式S2B2C商城小程序,探讨其在沉浸式体验营销中的应用。通过对比传统品鉴、工厂参观等初级体验方式,分析沉浸式体验的优势与价值…...

node.js的初步学习
那什么是node.js呢? 和JavaScript又是什么关系呢? node.js 提供了 JavaScript的运行环境。当JavaScript作为后端开发语言来说, 需要在node.js的环境上进行当JavaScript作为前端开发语言来说,需要在浏览器的环境上进行 Node.js 可…...

React父子组件通信:Props怎么用?如何从父组件向子组件传递数据?
系列回顾: 在上一篇《React核心概念:State是什么?》中,我们学习了如何使用useState让一个组件拥有自己的内部数据(State),并通过一个计数器案例,实现了组件的自我更新。这很棒&#…...
