ACwing算法备战蓝桥杯——Day30——树状数组
定义:
树状数组是一种数据结构,能将对一个区间内数据进行修改和求前缀和的这两种操作的最坏时间复杂度降低到O(logn);
| 变量名 | 变量数据类型 | 作用 |
| 数组a[] | int | 存储一段区间 |
| 数组tr[] | int | 表示树状数组 |
| 函数名 | 函数参数 | 组要作用 |
| lowbit() | int x | 返回x的二进制表示中最低的一位1的位置 |
| add() | int x,int v | 给区间内第x个数加上v |
| query() | int x | 返回区间前x个数的和 |
int a[N];
int tr[N];int lowbit(int x){return x&-x;
}void add(int x,int c){for(int i=x;i<=n;i+=lowbit(i)) tr[i]+=c;return;
}int query(int x){int res=0;for(int i=x;i;i-=lowbit(i)) res+=tr[i];return res;
}模板题:
题目:动态求连续区间的和
给定 n 个数组成的一个数列,规定有两种操作,一是修改某个元素,二是求子数列 [a,b] 的连续和。输入格式
第一行包含两个整数 n 和 m,分别表示数的个数和操作次数。第二行包含 n 个整数,表示完整数列。接下来 m 行,每行包含三个整数 k,a,b (k=0,表示求子数列[a,b]的和;k=1,表示第 a 个数加 b)。数列从 1 开始计数。输出格式
输出若干行数字,表示 k=0 时,对应的子数列 [a,b] 的连续和。数据范围
1≤n≤100000,
1≤m≤100000,
1≤a≤b≤n,
数据保证在任何时候,数列中所有元素之和均在 int 范围内。输入样例:
10 5
1 2 3 4 5 6 7 8 9 10
1 1 5
0 1 3
0 4 8
1 7 5
0 4 8
输出样例:
11
30
35代码与题解:
#include <iostream>
using namespace std;const int N=1e5+10;int tr[N];
int a[N];
int n,m;int lowbit(int x){return x&-x;
}void add(int x,int c){for(int i=x;i<=n;i+=lowbit(i)) tr[i]+=c;return;
}int query(int x){int res=0;for(int i=x;i;i-=lowbit(i)) res+=tr[i];return res;
}int main(){scanf("%d%d",&n,&m);for(int i=1;i<=n;i++){scanf("%d",&a[i]);}for(int i=1;i<=n;i++){add(i,a[i]);}while(m--){int k,a,b;scanf("%d%d%d",&k,&a,&b);if(k){add(a,b);}else {int anws=query(b)-query(a-1);printf("%d\n",anws);}} return 0;
}
相关文章:

ACwing算法备战蓝桥杯——Day30——树状数组
定义: 树状数组是一种数据结构,能将对一个区间内数据进行修改和求前缀和的这两种操作的最坏时间复杂度降低到O(logn); 实现所需变量 变量名变量数据类型作用数组a[]int存储一段区间数组tr[]int表示树状数组 主要操作 函数名函数参数组要作用lowbit()int…...
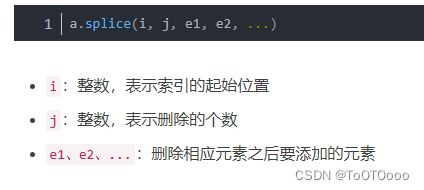
elementui + vue2实现表格行的上下移动
场景: 如上,要实现表格行的上下移动 实现: <el-dialogappend-to-bodytitle"条件编辑":visible.sync"dialogVisible"width"60%"><el-table :data"data1" border style"width: 100%&q…...
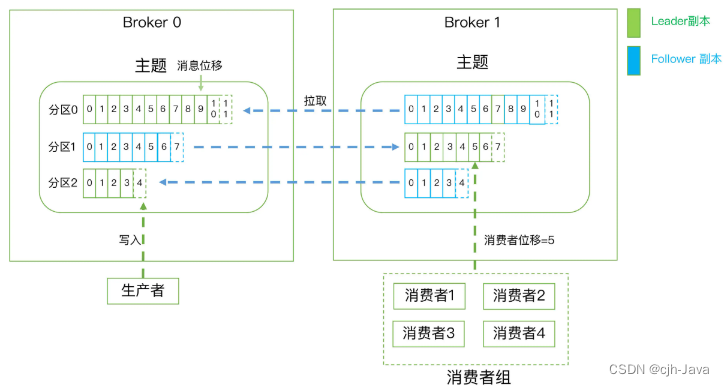
2、快速搞定Kafka术语
快速搞定Kafka术语 Kafka 服务端3层消息架构 Kafka 客户端Broker 如何持久化数据小结 Kafka 服务端 3层消息架构 第 1 层是主题层,每个主题可以配置 M 个分区,而每个分区又可以配置 N 个副本。第 2 层是分区层,每个分区的 N 个副本中只能有…...

CSS新手入门笔记整理:CSS3选择器
属性选择器 属性选择器,指的是通过“元素的属性”来选择元素的一种方式。 语法 元素[attr^"xxx"]{} 元素[attr$"xxx"]{} 元素[attr*"xxx"]{} 选择器 说明 E[attr^"xxx"] 选择元素E,其中E元素的attr属性是…...
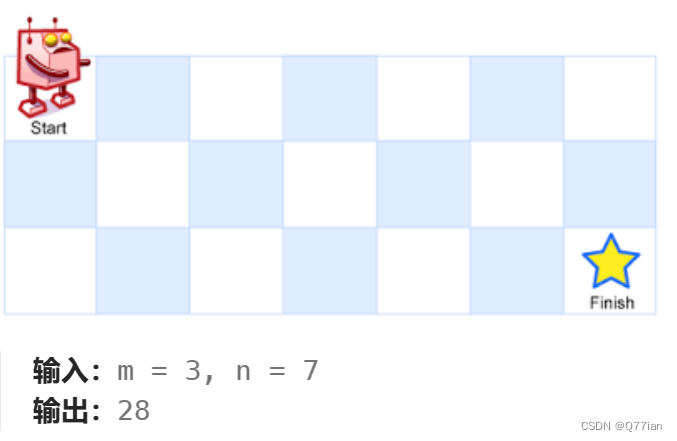
D34|不同路径
62.不同路径 初始思路: 1)确定dp数组以及下标的含义: dp[i][i]存放到第i1行和第i1列的方法数 2)确定递推公式: dp[i][i] dp[i -1][i] dp[i][i-1] 3)dp数组如何初始化 第0行是1; 第0列是1&a…...
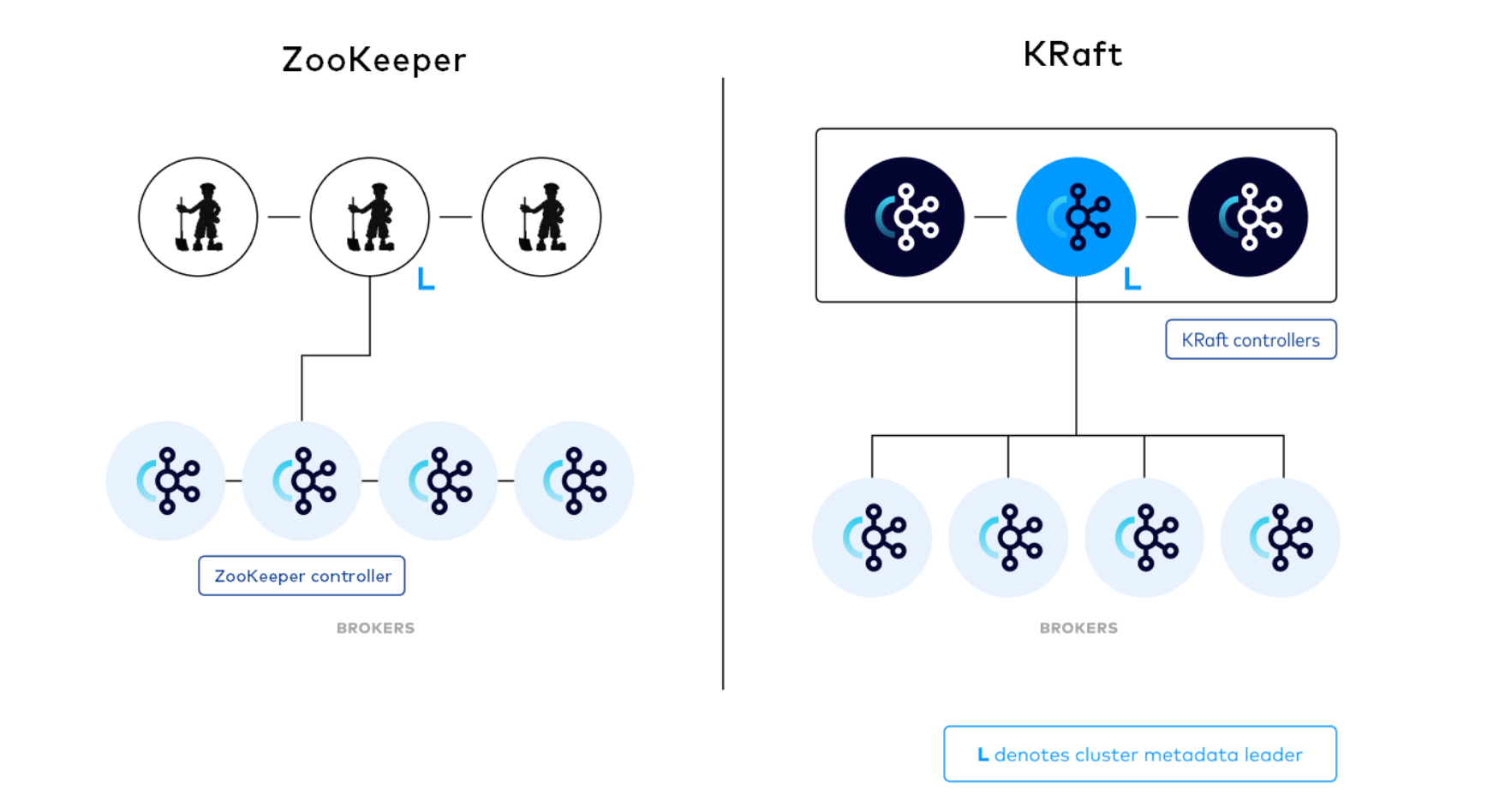
【运维】Kafka高可用: KRaft(不依赖zookeeper)集群搭建
文章目录 一. kafka kraft 集群介绍1. KRaft架构2. Controller 服务器3. Process Roles4. Quorum Voters5. kraft的工作原理 ing 二. 集群安装1. 安装1.1. 配置1.2. 格式化 2. 启动测试2.1. 启功节点服务2.2. 测试 本文主要介绍了 kafka raft集群架构: 与旧架构的不…...

Python 自动化之批量处理文件(一)
批量新建目录、文档Pro版本 文章目录 批量新建目录、文档Pro版本前言一、做成什么样子二、基本思路1.引入库2.基本架构 三、用户输入模块四、数据处理模块1.excel表格数据获取2.批量数据的生成 总结 前言 我来写一个不一样的批量新建吧。在工作中,有些同学应该会遇…...

力扣72. 编辑距离
动态规划 思路: 假设 dp[i][j] 是 word1 前 i 个字母到 word2 前 j 个字母的编辑距离;那么状态 dp[i][j] 状态的上一个状态有: dp[i - 1][j],word1 前 i - 1 个字母到 word2 前 j 个字母的编辑距离,此状态再插入一个字…...
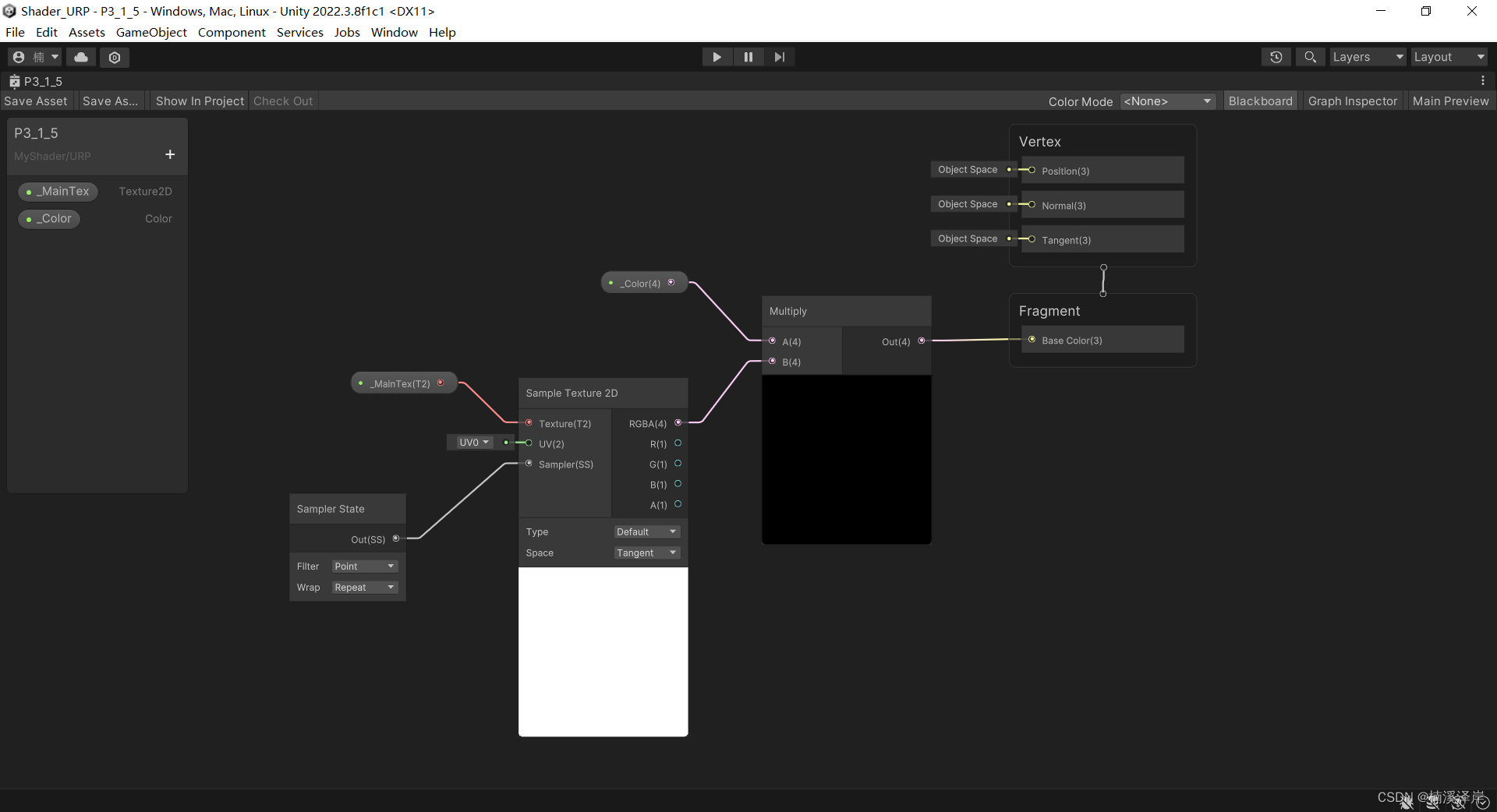
Unity中 URP Shader 的纹理与采样器的分离定义
文章目录 前言一、URP Shader 纹理采样的实现1、在属性面板定义一个2D变量用于接收纹理2、申明纹理3、申明采样器4、进行纹理采样 二、申明纹理 和 申明采样器内部干了什么1、申明纹理2、申明采样器 三、采样器设置采样器的传入格式1、纹理设置中,可以看见我们的采样…...

Electron学习第一天 ,启动项目
之前在安装官网的步骤操作,结果报错,找了好多办法,最后这种办法成功启动项目,并且没有报错,特此记录 特别提醒,最好安装淘宝镜像,npm 太慢,会导致报错问题,解决起来个人觉…...

WebService技术--随笔1
1.WebService 发展史 创建阶段(1990 年代末至 2000 年代初):在这个阶段,XML-RPC 和 SOAP 协议被引入,为跨平台和跨语言的应用程序集成提供了基础。XML-RPC 提供了一种基于 XML 的远程过程调用机制,而 SOAP…...

如何使用Docker将.Net6项目部署到Linux服务器(一)
目录 一 配置服务器环境 1.1 配置yum 1.1.1 更新yum包 1.1.2 yum命令 1.2 配置docker …...

第4章-第3节-Java中跟数组相关的几个算法以及综合应用
在写这篇博文之前,先大概说明一下,就是很常见的数组算法如求最大值、一维数组的遍历等,这里就不去专门说明了,只说一些有代表性的,然后就是冒泡排序算法很容易查阅到,这里也不专门说明了,只说明…...
AlexNet(pytorch)
AlexNet是2012年ISLVRC 2012(ImageNet Large Scale Visual Recognition Challenge)竞赛的冠军网络,分类准确率由传统的 70%提升到 80% 该网络的亮点在于: (1)首次利用 GPU 进行网络加速训练。 ÿ…...

【单调栈 】LeetCode321:拼接最大数
作者推荐 【动态规划】【广度优先搜索】LeetCode:2617 网格图中最少访问的格子数 本文涉及的知识点 单调栈 题目 给定长度分别为 m 和 n 的两个数组,其元素由 0-9 构成,表示两个自然数各位上的数字。现在从这两个数组中选出 k (k < m n) 个数字…...

TikTok与虚拟现实的完美交融:全新娱乐时代的开启
TikTok,这个风靡全球的短视频平台,与虚拟现实(VR)技术的深度结合,为用户呈现了一场全新的娱乐盛宴。虚拟现实技术为TikTok带来了更丰富、更沉浸的用户体验,标志着全新娱乐时代的开启。本文将深入探讨TikTok…...

PXI/PCIe/VPX机箱 ARM|x86 + FPGA测试测量板卡解决方案
PXI便携式测控系统是一种基于PXI总线的便携式测试测控系统,它填补了现有台式及机架式仪器在外场测控和便携测控应用上的空白,在军工国防、航空航天、兵器电子、船舶舰载等各个领域的外场测控场合和科学试验研究场合都有广泛的应用。由于PXI便携式测控系统…...

ES6 面试题 | 12.精选 ES6 面试题
🤍 前端开发工程师(主业)、技术博主(副业)、已过CET6 🍨 阿珊和她的猫_CSDN个人主页 🕠 牛客高级专题作者、在牛客打造高质量专栏《前端面试必备》 🍚 蓝桥云课签约作者、已在蓝桥云…...

【linux】Debian不能运行sudo的解决
一、问题: sudo: 没有找到有效的 sudoers 资源,退出 sudo: 初始化审计插件 sudoers_audit 出错 二、可用的方法: 出现 "sudo: 没有找到有效的 sudoers 资源,退出" 和 "sudo: 初始化审计插件 sudoers_audit 出错&q…...

讲解ThinkPHP的链式操作
数据库提供的链式操作方法,可以有效的提高数据存取的代码清晰度和开发效率,并且支持所有的CURD操作。 使用也比较简单,假如我们现在要查询一个User表的满足状态为1的前10条记录,并希望按照用户的创建时间排序 Db::table(think_u…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...
