【线性代数】期末速通!
1. 行列式的性质
1.1 求一个行列式的值
特殊地,对角线左下全为0,结果为对角线乘积。行 r 列 c
1.2 性质
- 某行(列)加上或减去另一行(列)的几倍,行列式不变
- 某行(列)乘 k,等于 k 乘此行列式
- 互换两行(列),行列式变号
2. 行列式的计算及应用
见书 P22,P18
2.1 公式应用
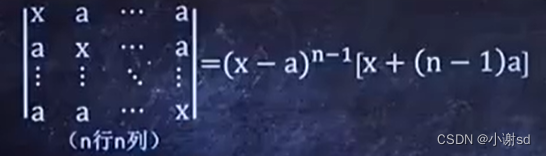
2.2 公式应用
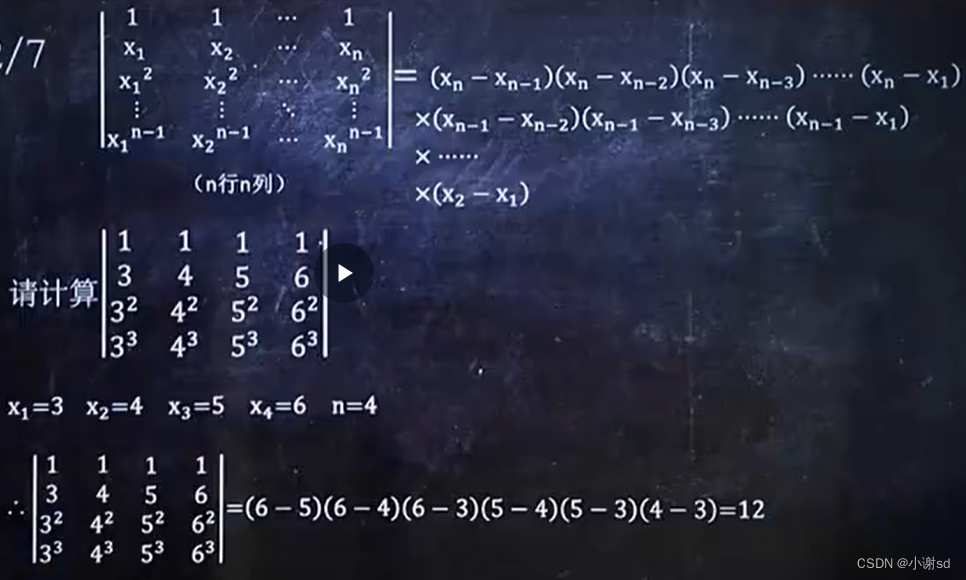
2.3 性质应用
①两行(列)相同或成比例时,行列式为0
②某行(列)为两项相加减时,行列式可拆成两个行列式相加减

2.4 求余子式(M)、代数余子式(A)


2.5 公式应用

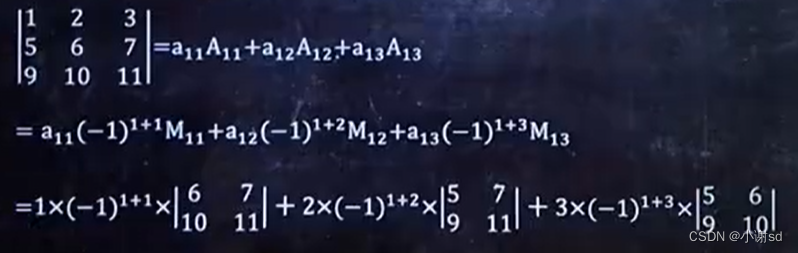
2.6 多个 A 或 M 相加减

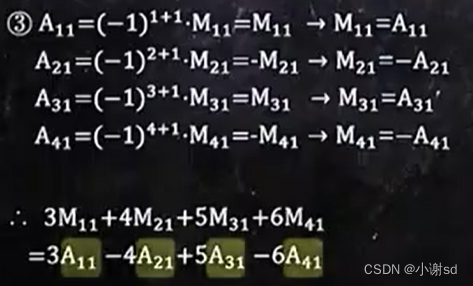
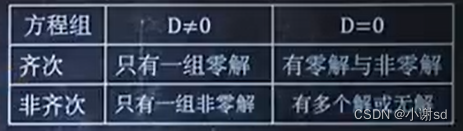
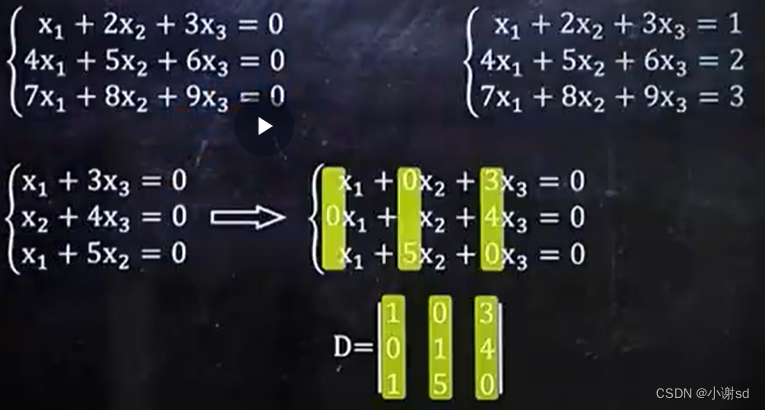
2.7 给一个方程组,判断其解的情况
3. 矩阵的运算上
3.1 矩阵加减

3.2 矩阵相乘
前行乘后列
结果行数等于前项,结果列数等于后项

特殊情况:


3.3 矩阵取绝对值

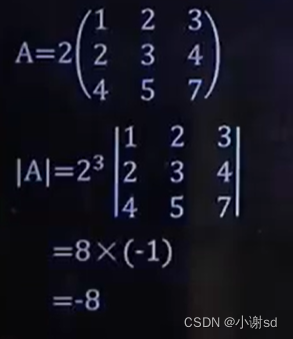

| A ^-1 | = | A | ^-1
行矩阵或者列矩阵的行列式的值就是各个数相乘。
对角矩阵是一个主对角线之外的元素皆为0的矩阵,常写为diag(a1,a2,…,an) 。

4. 矩阵的运算下
4.1 转置
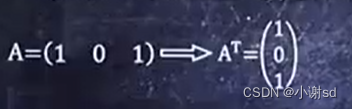
先用行乘列,简化运算。
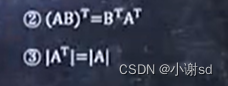
4.2 证明矩阵可逆


4.3 求逆矩阵


A 和 E 同时进行变换。
4.4 公式应用

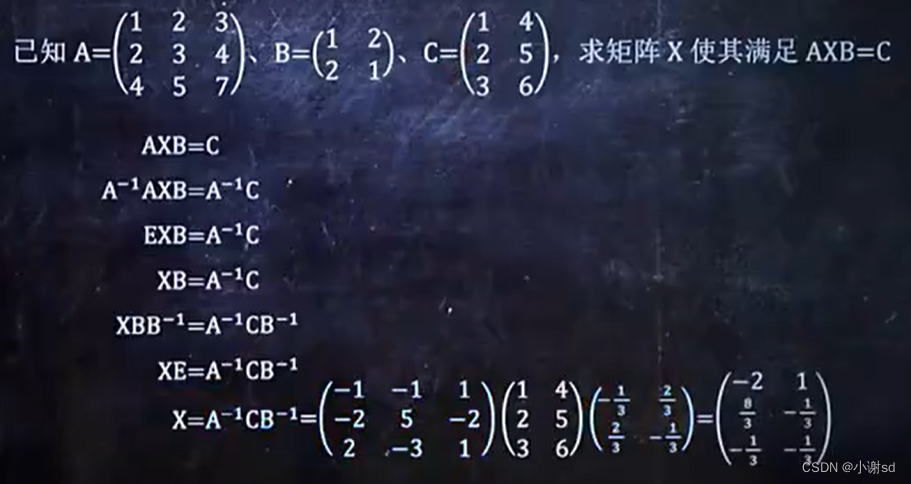
4.5 公式应用


4.6 求矩阵的秩或未知数
对矩阵进行行变换,是下行左端的0比上行多,直到下面行全为0为止。

秩为不全为0的行数。

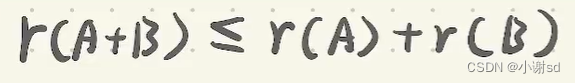
一个矩阵(非零)和它的转置矩阵相乘的积的秩为 1。零矩阵时为零。

5. 向量组与线性空间
5.1 判断某向量是否可以由某向量组线性表示

5.2 判断某个向量组是否线性相关


5.3 已知三维向量空间的一组基底,求某一向量在此基底下的坐标

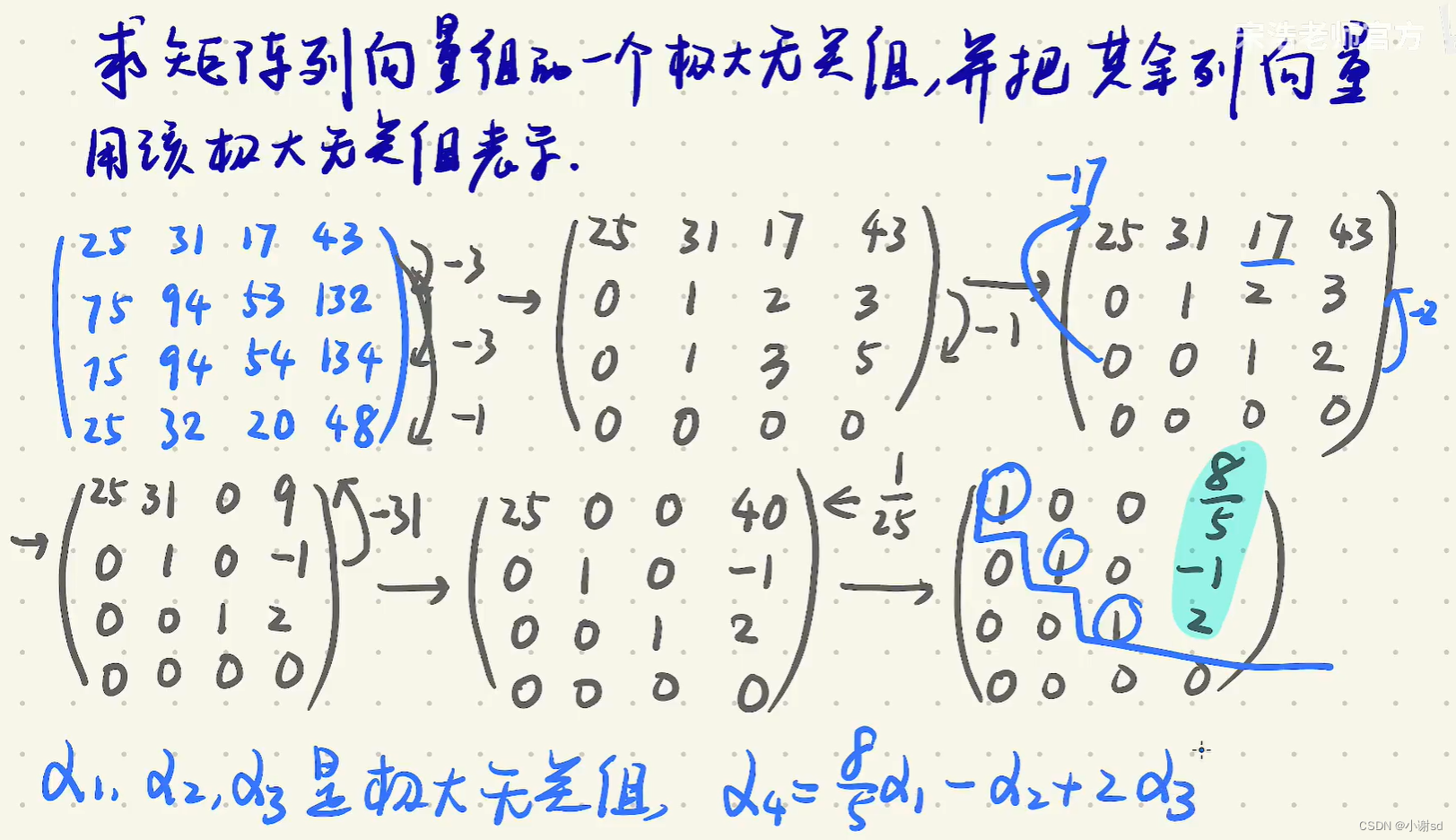
5.4 求几个行向量的极大无关组

操作步骤里面只有第一行和第四行做过交换,因此把前面的序号从1,2,3,4变为4,2,3,1。

6. 解方程组
6.1 判断方程组解的情况



6.2 解方程组(通解)

第②步:因为秩为3,所以将矩阵的前三行前三列的对角线变为1,其他变为0。

6.3 求方程组的通解、特解、基础解系
通解即为上述 6.2 中解出的方程组的解。
特解即为将 k 附任意值,得出的解。
基础解系是 k 后面的矩阵:

6.4 已知某方程组的多个特解,求某齐次方程组的通解
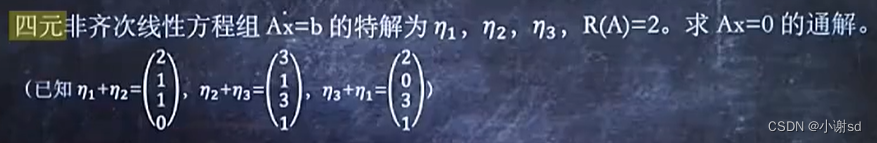
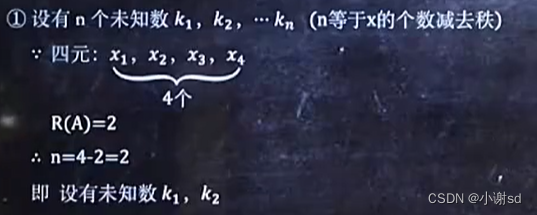

X1和X2不成比例就是线性无关。
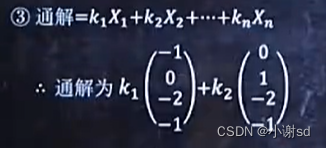
6.5 已知某方程组的多个特解,求某非齐次方程组的通解

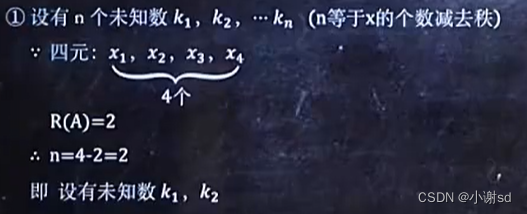


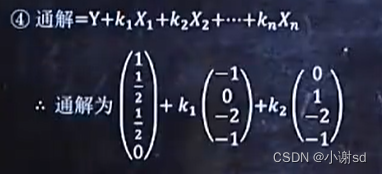
通解 = Ax=b 的一个特解 + 导出组的基础解系的线性组合

6.6 判断解集合中线性无关的解向量个数

7. 方阵对角化及其应用
7.1 规范正交化

比如:
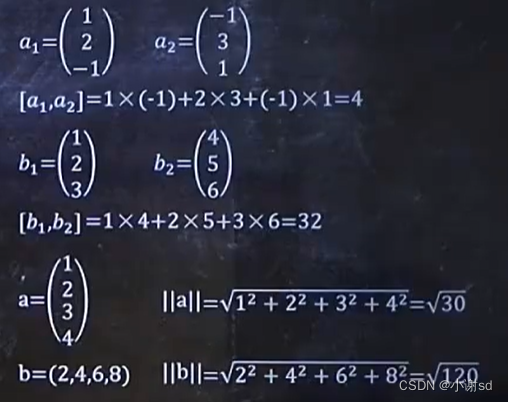

7.2 求矩阵的特征值


7.3 求矩阵的特征向量

先求特征值。

7.4 判断方阵是否与对角阵相似


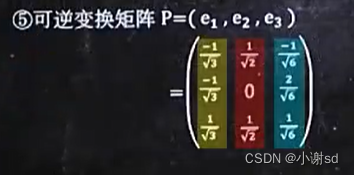
7.5 求方阵对应的对角阵及可逆变换矩阵


7.6 已知条件,求关于 A 的复杂式子
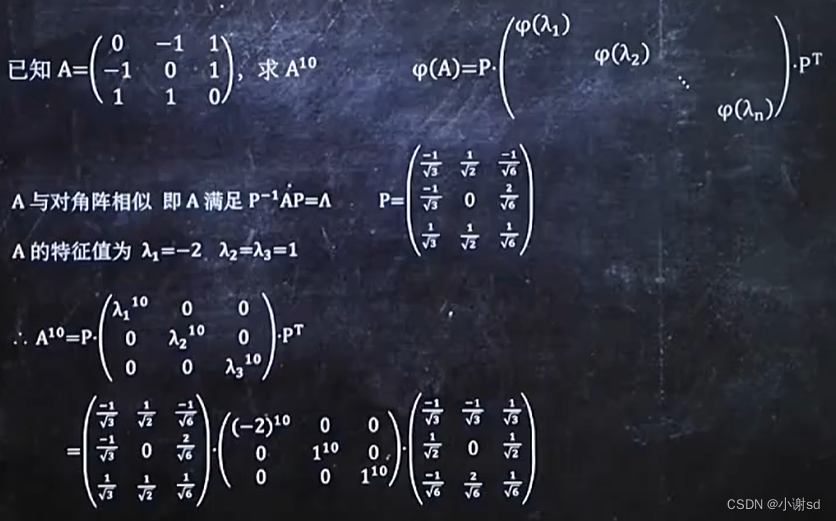
8. 二次型
8.1 求二次型对应的系数矩阵

8.2 把二次型化成标准型

8.3 把二次型化成规范形

8.4 用配方法把二次型化成标准型

8.5 判断二次型的正定性
系数矩阵的顺序主子式均大于 0 时,该二次型正定。

8.6 二次型为正定的等价条件

满足任意一条即可。
9. 其他题型
9.1 化为最简形矩阵
行最简型:①画楼梯②非零行首个一(也就是阶梯处)所在的列其他数都为零
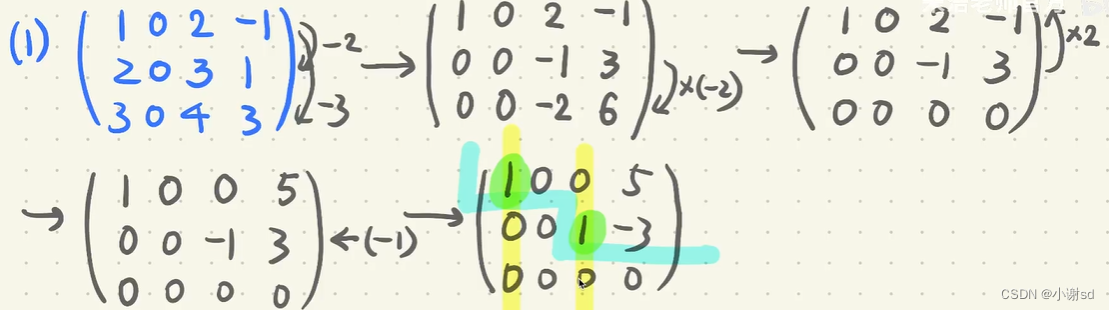
此题型有时答案可能不唯一。

(A矩阵的逆可以理解为 1 / A)

9.2 判断一个矩阵是否可逆
证明一个矩阵可逆的方法有5种:
(1)看这个矩阵的行列式值是否为0,若不为0,则可逆;
(2)看这个矩阵的秩是否为n,若为n,则矩阵可逆;
(3)定义法:若存在一个矩阵B,使矩阵A使得AB=BA=E,则矩阵A可逆,且B是A的逆矩阵;
(4)对于齐次线性方程AX=0,若方程只有零解,那么这个矩阵可逆,反之若有无穷解则矩阵不可逆;
(5)对于非齐次线性方程AX=b,若方程只有特解,那么这个矩阵可逆,反之若有无穷解则矩阵不可逆。
9.3 判断矩阵是否相似合同

9.4 矩阵消去律
消去左矩阵需要左矩阵满秩,消去右矩阵需要右矩阵满秩。
矩阵消去律详解


相关文章:

【线性代数】期末速通!
1. 行列式的性质 1.1 求一个行列式的值 特殊地,对角线左下全为0,结果为对角线乘积。行 r 列 c 1.2 性质 某行(列)加上或减去另一行(列)的几倍,行列式不变某行(列)乘 …...

速盾网络:业务卓越,数字安全的领先者
在数字时代的浪潮中,业务成功需要强大的数字基石。速盾网络以其出色的CDN加速、高防IP、SDK游戏盾和抗DDoS攻击等业务,成为业界领先的数字安全保障者,为您的业务提供全方位的支持与保护。 CDN加速:业务飞跃的翅膀 速盾网络以全球…...
Python 全栈体系【四阶】(七)
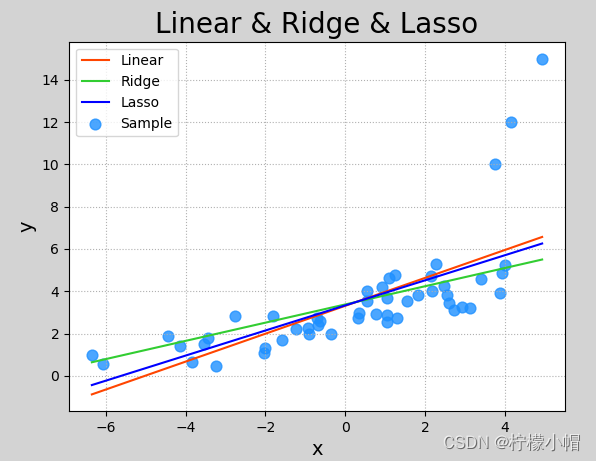
第四章 机器学习 六、多项式回归 1. 什么是多项式回归 线性回归适用于数据呈线性分布的回归问题。如果数据样本呈明显非线性分布,线性回归模型就不再适用(下图左),而采用多项式回归可能更好(下图右)。例…...

智能优化算法应用:基于蛾群算法3D无线传感器网络(WSN)覆盖优化 - 附代码
智能优化算法应用:基于蛾群算法3D无线传感器网络(WSN)覆盖优化 - 附代码 文章目录 智能优化算法应用:基于蛾群算法3D无线传感器网络(WSN)覆盖优化 - 附代码1.无线传感网络节点模型2.覆盖数学模型及分析3.蛾群算法4.实验参数设定5.算法结果6.参考文献7.MA…...

Tekton 克隆 git 仓库
Tekton 克隆 git仓库 介绍如何使用 Tektonhub 官方 git-clone task 克隆 github 上的源码到本地。 git-clone task yaml文件下载地址:https://hub.tekton.dev/tekton/task/git-clone 查看git-clone task yaml内容: 点击Install,选择一种…...

高通平台开发系列讲解(AI篇)SNPE工作流程介绍
文章目录 一、转换网络模型二、量化2.1、选择量化或非量化模型2.2、使用离线TensorFlow或Caffe模型2.3、使用非量化DLC初始化SNPE2.4、使用量化DLC初始化SNPE三、准备输入数据四、运行加载网络沉淀、分享、成长,让自己和他人都能有所收获!😄 📢本篇章主要介绍SNPE模型工作…...

YoloV8改进策略:ASF-YOLO,结合了空间和尺度特征在小目标和密集目标场景有效涨点
摘要 本文提出了一种新型的Attentional Scale Sequence Fusion based You Only Look Once (YOLO)框架(ASF-YOLO),该框架结合了空间和尺度特征,以实现准确且快速的细胞实例分割。该框架建立在YOLO分割框架之上,采用Scale Sequence Feature Fusion (SSFF)模块增强网络的多尺…...
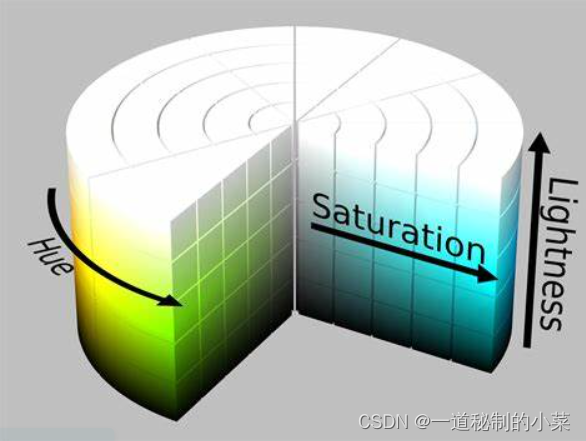
OpenCV-8RGB和BGR颜色空间
一. RGB和BGR 最常见的色彩空间就是RGB,人眼也是基于RGB的色彩空间去分辨颜色。 OpenCV默认使用的是BGR. BGR和RGB色彩空间的区别在于图片在色彩通道上的排列顺序不同。 二.HSV, HSL和YUV 1.HSV(HSB) OpenCV用的最多的色彩空间是HSV. Hue:色相&…...
阿里云主导《Serverless 计算安全指南》国际标准正式立项!
日前,在韩国召开的国际电信联盟电信标准分局 ITU-T SG17 全会上,由阿里云主导的《Serverless 计算安全指南》国际标准正式立项成功。 图 1 项目信息 在现今数字化时代,Serverless 计算正逐渐成为云计算的一个新的发展方向,其灵活…...

YOLOv5改进 | 2023 | CARAFE提高精度的上采样方法(助力细节长点)
一、本文介绍 本文给大家带来的CARAFE(Content-Aware ReAssembly of FEatures)是一种用于增强卷积神经网络特征图的上采样方法。其主要旨在改进传统的上采样方法(就是我们的Upsample)的性能。CARAFE的核心思想是:使用…...
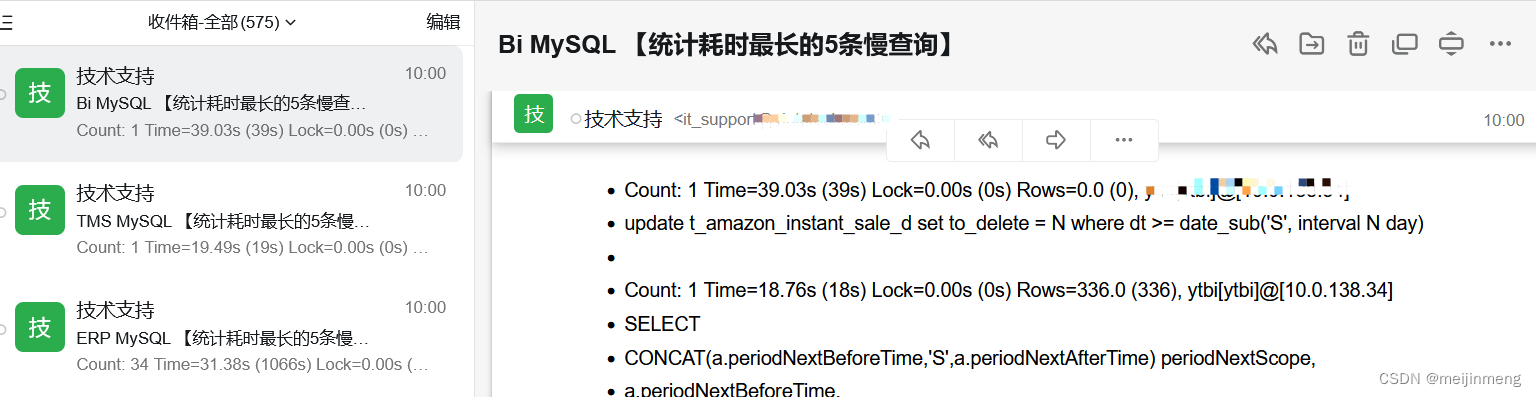
AWS RDS慢日志文件另存到ES并且每天发送邮件统计慢日志
1.背景:需要对aws rds慢日志文件归档到es,让开发能够随时查看。 2.需求:并且每天把最新的慢日志,过滤最慢的5条sql 发送给各个产品线的开发负责人。 3.准备: aws ak/sk ,如果rds 在不同区域需要认证不同的…...

如何在断线后不重连加入音视频房间
RTC 房间断网后,默认是一直尝试重连的,例如当主播再次联网重连成功后,会自动发布之前在发布的音视频流。针对某些不想断网后重新加入连接的场景,需要如下配置: 1、配置断开后不去重连(这种情况也会重连 4 次…...

RabbitMq交换机详解
目录 1.交换机类型2.Fanout交换机2.1.声明队列和交换机2.2.消息发送2.3.消息接收2.4.总结 3.Direct交换机3.1.声明队列和交换机3.2.消息接收3.3.消息发送3.4.总结 4.Topic交换机4.1.说明4.2.消息发送4.3.消息接收4.4.总结 5.Headers交换机5.1.说明5.2.消息发送5.3.消息接收5.4.…...

智能优化算法应用:基于适应度相关算法3D无线传感器网络(WSN)覆盖优化 - 附代码
智能优化算法应用:基于适应度相关算法3D无线传感器网络(WSN)覆盖优化 - 附代码 文章目录 智能优化算法应用:基于适应度相关算法3D无线传感器网络(WSN)覆盖优化 - 附代码1.无线传感网络节点模型2.覆盖数学模型及分析3.适应度相关算法4.实验参数设定5.算法…...

spring之基于注解管理Bean
学习的最大理由是想摆脱平庸,早一天就多一份人生的精彩;迟一天就多一天平庸的困扰。各位小伙伴,如果您: 想系统/深入学习某技术知识点… 一个人摸索学习很难坚持,想组团高效学习… 想写博客但无从下手,急需…...

Wireshark在云计算中的应用
第一章:Wireshark基础及捕获技巧 1.1 Wireshark基础知识回顾 1.2 高级捕获技巧:过滤器和捕获选项 1.3 Wireshark与其他抓包工具的比较 第二章:网络协议分析 2.1 网络协议分析:TCP、UDP、ICMP等 2.2 高级协议分析:HTTP…...
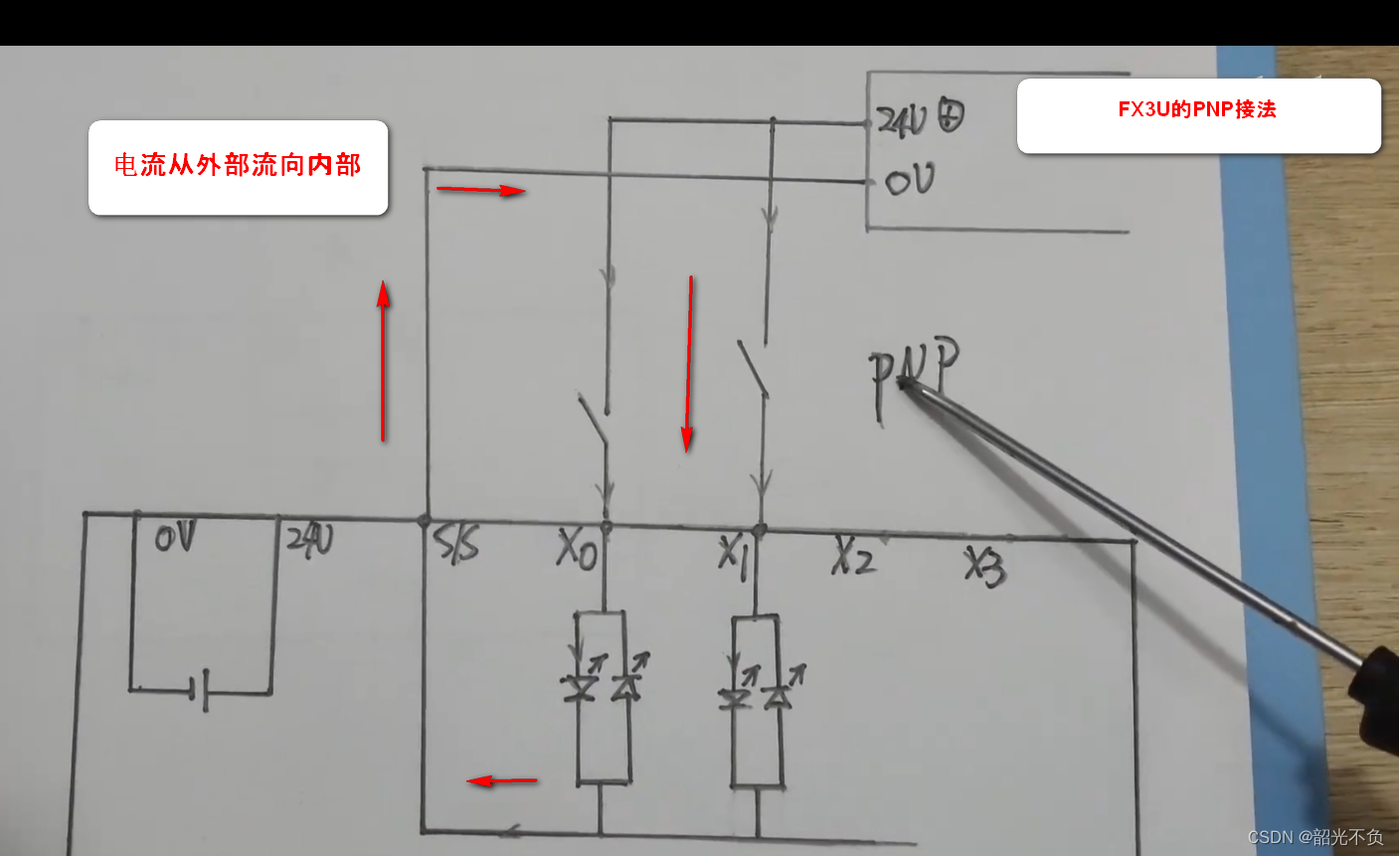
三菱plc学习入门(一,认识三菱plc)
今天就开始对三菱的plc软件入一个门,希望小编的文章对读者和初学者有所帮助!欢迎评论指正,废话不多说,下面开始学习。 目录 plc的型号介绍 M表示什么? T表示什么? R表示什么? 为什么三菱没…...
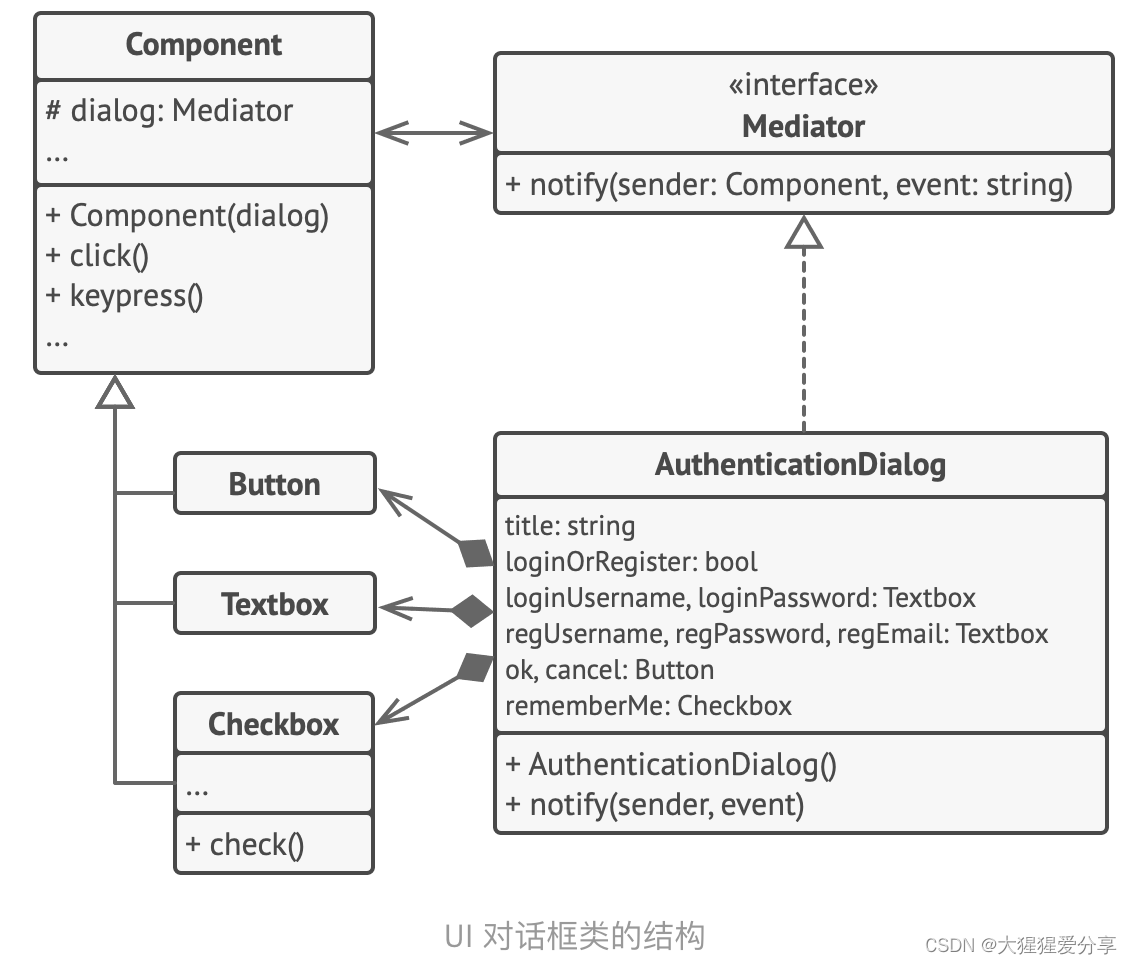
设计模式——中介者模式
引言 中介者模式是一种行为设计模式, 能让你减少对象之间混乱无序的依赖关系。 该模式会限制对象之间的直接交互, 迫使它们通过一个中介者对象进行合作。 问题 假如你有一个创建和修改客户资料的对话框, 它由各种控件组成, 例如…...
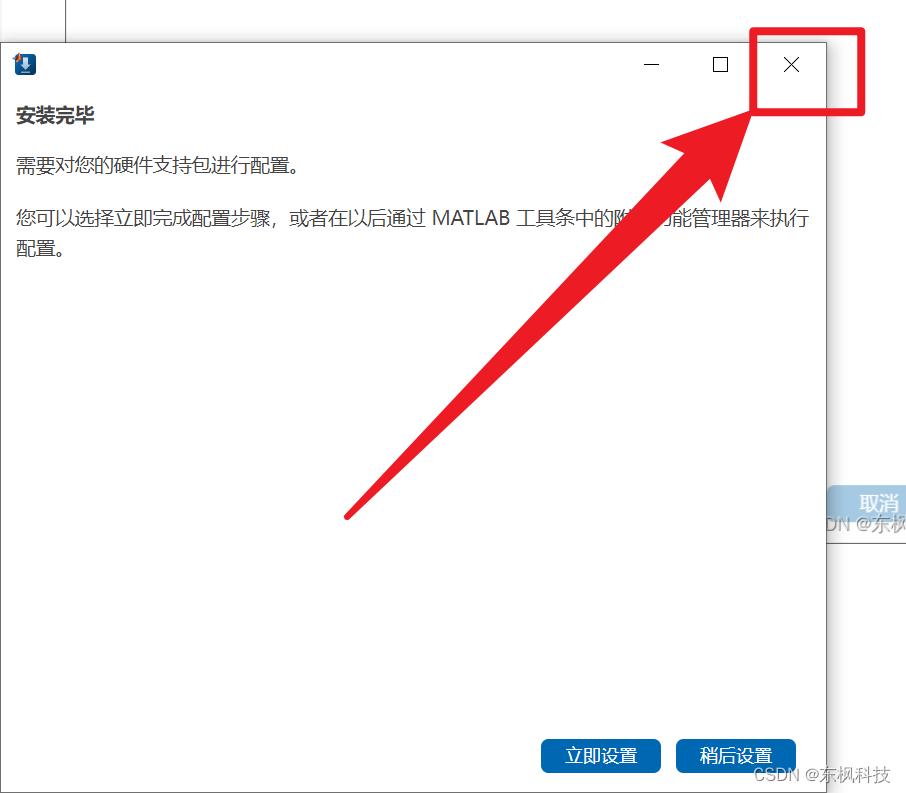
【 USRP安装教程】MATLAB 2023B
步骤 matlabdocusrp驱动包 doc 安装包内容列表 双击“R2023b_Doc_Windows.iso” 打开cmd 查看盘符 切换盘符 因为是F盘,所以cmd输入:“F:” F:进入可安装界面 cd F:\bin\win64安装离线文档库 .\mpm install-doc --matlabroot"C:\MATLAB\R202…...

AI绘画中UNet用于预测噪声
介绍 在AI绘画领域中,UNet是一种常见的神经网络架构,广泛用于图像相关的任务,尤其是在图像分割领域中表现突出。UNet最初是为了解决医学图像分割问题而设计的,但其应用已经扩展到了多种图像处理任务。 特点 对称结构:…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

华为OD机试-最短木板长度-二分法(A卷,100分)
此题是一个最大化最小值的典型例题, 因为搜索范围是有界的,上界最大木板长度补充的全部木料长度,下界最小木板长度; 即left0,right10^6; 我们可以设置一个候选值x(mid),将木板的长度全部都补充到x,如果成功…...

tomcat指定使用的jdk版本
说明 有时候需要对tomcat配置指定的jdk版本号,此时,我们可以通过以下方式进行配置 设置方式 找到tomcat的bin目录中的setclasspath.bat。如果是linux系统则是setclasspath.sh set JAVA_HOMEC:\Program Files\Java\jdk8 set JRE_HOMEC:\Program Files…...

自然语言处理——文本分类
文本分类 传统机器学习方法文本表示向量空间模型 特征选择文档频率互信息信息增益(IG) 分类器设计贝叶斯理论:线性判别函数 文本分类性能评估P-R曲线ROC曲线 将文本文档或句子分类为预定义的类或类别, 有单标签多类别文本分类和多…...

React核心概念:State是什么?如何用useState管理组件自己的数据?
系列回顾: 在上一篇《React入门第一步》中,我们已经成功创建并运行了第一个React项目。我们学会了用Vite初始化项目,并修改了App.jsx组件,让页面显示出我们想要的文字。但是,那个页面是“死”的,它只是静态…...
