sklearn多项式回归和线性回归
什么是线性回归?
回归分析是一种统计学方法,用于研究自变量和因变量之间的关系。它是一种建立关系模型的方法,可以帮助我们预测和解释变量之间的相互作用。 回归分析通常用于预测一个或多个因变量的值,这些因变量的值是由一个或多个自变量的值所决定的。回归分析的目标是建立一个数学模型来描述因变量和自变量之间的关系。 这个数学模型可以是线性或非线性的,可以包含一个或多个自变量。通过回归分析,我们可以使用已知的自变量和因变量值来计算模型参数,然后使用这些参数来预测因变量值。 回归分析被广泛应用于各种领域,包括经济学、社会学、医学、环境科学和工程学等。它可以用于研究许多不同的问题,如房价预测、销售预测、股票价格预测、人口增长预测等等。线性回归需要满足的条件: (1)自变量和因变量在理论上有因果关系;(2)因变量为连续型变量;(3)各自变量与因变量之间存有线性关系;(4)残差要满足正态性、独立性、方差齐性。(5)多个自变量不存在多重共线性其中,线性(Linear)、正态性(Normal)、独立性(independence)、方差齐性(Equal Variance),俗称LINE,是线性回归分析的四大基本前提条件。
sklearn的线性回归:
- 准备工作
from sklearn.linear_model import LinearRegression- 创建模型:
linear =LinearRegression()- 拟合模型:
linear.fit(x,y)- 模型的预测值:
linear.predict(输入数据)- 线性回归模型的权重
linear.coef_和偏置linear.intercept_
class sklearn.linear_model.LinearRegression (fit_intercept=True, normalize=False, copy_X=True, n_jobs=None)
参数
含义
fit_intercept:布尔值,可不填,默认为True是否计算此模型的截距。如果设置为False,则不会计算截距
normalize:布尔值,可不填,默认为False,当fit_intercept设置为False时,将忽略此参数。如果为True,则特征矩阵X在进入回归之前将会被减去均值(中心化)并除以L2范式(缩放)。如果你希望进行标准化,请在fit数据之前用preprocessing模块中的标准化专用类StandardScaler
copy_X:布尔值,可不填,默认为True,如果为真,将在X.copy()上进行操作,否则的话原本的特征矩阵X可能被线性回归影响并覆盖
n_jobs:整数或者None,可不填,默认为None,用于计算的作业数。只在多标签的回归和数据量足够大的时候才生效。除非None在joblib.parallel_backend上下文中,否则None统一表示为1。如果输入 -1,则表示使用全部的CPU来进行计算。
线性回归代码:
线性回归直接预测血糖值:return: None"""# 获取数据lb = readcvs()# print(lb)# 分割数据集到训练集和测试集,按照75%:25%的比例进行数据分配训练数据和测试数据x_train, x_test, y_train, y_test = train_test_split(lb['data'], lb['target'], test_size=0.2)# 进行标准化处理(目标值要进行标准化处理)# 特征值和目标值都必须进行标准化处理, 实例化两个标准化API# 标准化也就是归一化处理# std_x = StandardScaler()# # 标准化训练数据# x_train = std_x.fit_transform(x_train)# # 标准化测试数据# x_test = std_x.transform(x_test)## # 目标值# std_y = StandardScaler()# # 标准化目标训练数据(因为数据是[y,y,1,1,1,1,...]变换成[[],[],[],[],[]...])进行变换# y_train = std_y.fit_transform(y_train.reshape(-1, 1))# # 标准化目标测试数据(同上)# y_test = std_y.transform(y_test.reshape(-1, 1))# estimator预测# 正规方程求解方式预测结果lr = LinearRegression()print("多项式参数:",l_data)# 对训练数据进行拟合lr.fit(x_train, y_train)# # 查看w的参数print('w参数',lr.coef_)# # 查看b的参数print('b参数',lr.intercept_)# 保存训练模型# 预测测试集的房子价格# y_lr_predict = std_y.inverse_transform(lr.predict(x_test))y_lr_predict = lr.predict(x_test)print("正规方程测试集里面每个血糖的预测: ", y_lr_predict)# print("正规方程的均方误差: ", mean_squared_error(std_y.inverse_transform(y_test), y_lr_predict))score_ = lr.score(x_test, y_test)print('模型得分', score_)# 保存血糖模型数据if score_ > 0.2:joblib.dump(lr, "./model/blood.pkl")return score_def train_():count=0sys.setrecursionlimit(100000) # 设置递归深度list=[]#循环10000次for i in range(10000):score = train()list.append(score)count = count+1print("最高得分", max(list))if score>0.2:breakprint("最高得分",max(list))#加载模型准备预测
def predict():list=[[1, 80.0, 179, 55,421,0]]value=np.array(list)# 导入血糖模型数据lr = joblib.load("./model/blood.pkl")#直接预测结果y_lr_predict=lr.predict(value)print(y_lr_predict)#返回模型预测出来的血糖值return y_lr_predictif __name__ == "__main__":train_()多项式回归:
多项式回归:
from sklearn.preprocessing import PolynomialFeatures
# 设置多项式阶数为2,其他值默认
# degree 多项式阶数
poly = PolynomialFeatures(degree=2)
res = poly.fit_transform(X)PolynomialFeatures详细探讨 现在有(a,b)两个特征,使用degree=2的二次多项式则为(1,a, a^2, ab, b ,b^2)。 PolynomialFeatures主要有以下几个参数:degree:度数,决定多项式的次数interaction_only: 默认为False,字面意思就是只能交叉相乘,不能有a^2这种.include_bias: 默认为True, 这个bias指的是多项式会自动包含1,设为False就没这个1了.order:有"C" 和"F" 两个选项。官方写的是在密集情况(dense case)下的输出array的顺序,F可以加快操作但可能使得subsequent estimators变慢。
如何控制多项式回归的系数:a=[[2,3]] 或者a=[[2],[3]]
from sklearn.preprocessing import PolynomialFeatures
a=[[2,3]](相当于[[x1,x2]])
pf=PolynomialFeatures(degree=2)
print(pf.fit_transform(a)) #会产生多项式的系数
#[[1. 2. 3. 4. 6. 9.]] 相当于(1+2+3+2*2+2*3+3*3)
pf=PolynomialFeatures(degree=2,include_bias=False)
print(pf.fit_transform(a))
#[[2. 3. 4. 6. 9.]]
pf=PolynomialFeatures(degree=2,interaction_only=True)
print(pf.fit_transform(a))
#[[1. 2. 3. 6.]]如果是c=[[a],[b]]这种形式,生成的多项式就没有ab交叉项了,只有[[1,a,a^2], [1,b,b^2]] 。
c=[[2],[3]]
print(pf.fit_transform(c))
[[1. 2. 4.][1. 3. 9.]]转换器Transformers 通常与分类器、回归器或其他估计器相结合,构成一个复合估计器。最常见的工具是pipeline。
利用Pipline进项多项式和线性回归合并,这样会产生非线性的回归
lr = Pipeline([('poly', PolynomialFeatures(degree=2)),('clf', LinearRegression())])
lr.fit(x_train, y_train)多项式和线性回归相结合
lr = LinearRegression()
pf=PolynomialFeatures(degree=2)
lr.fit(pf.fit_transform(X), y)
print(lr.coef_)
print(lr.intercept_)
对应w和b(对应多项式的斜率和截距)
[0.1 1.413 -0.435]
-1.584092回归的俩中线性和非线性:
# 线性回归
clf1 = LinearRegression()
clf1.fit(x, y)
y_l = clf1.predict(x) # 线性回归预测值# 非线性回归
ployfeat = PolynomialFeatures(degree=3) # 根据degree的值转换为相应的多项式(非线性回归)
x_p = ployfeat.fit_transform(x)
clf2 = LinearRegression()
clf2.fit(x_p, y)
相关文章:

sklearn多项式回归和线性回归
什么是线性回归? 回归分析是一种统计学方法,用于研究自变量和因变量之间的关系。它是一种建立关系模型的方法,可以帮助我们预测和解释变量之间的相互作用。 回归分析通常用于预测一个或多个因变量的值,这些因变量的值是由一个或多…...
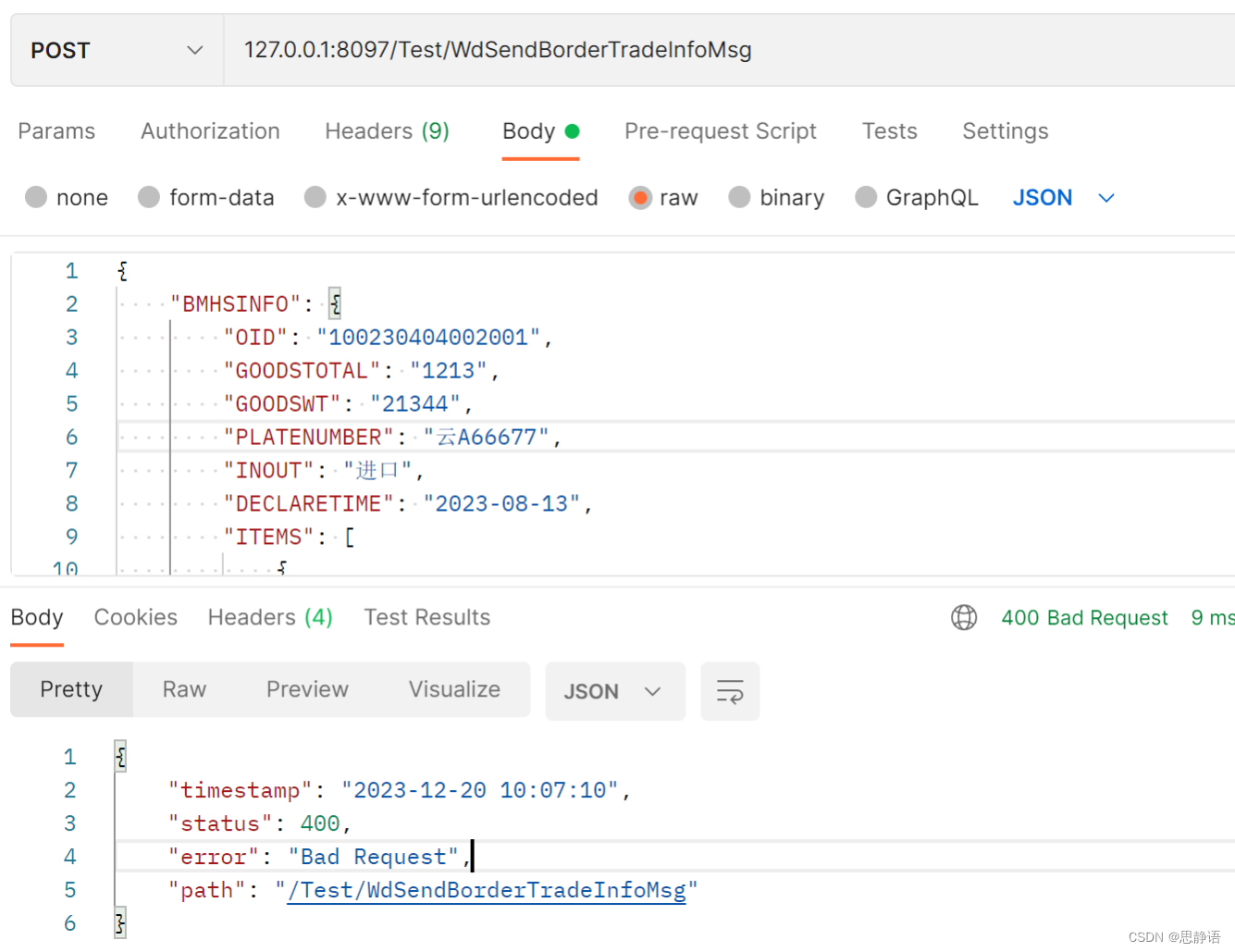
Postman报:400 Bad Request
● 使用Postman发送Post请求报400,入参为JSON; 二、分析 1、Postman请求并没有请求到后台Api(由于语法错误,服务器无法理解请求); 2、入参出错范围:cookie、header、body、form-data、x-www-f…...

apache poi_5.2.5 实现表格内某一段单元格的复制
apache poi_5.2.5 实现表格内,某一段单元格的复制。 实现思路 1.定位开始位置 2.从开始位置之后,在行索引集合中添加行索引下标 3.截至到结束位置。 4.对行索引集合去重,并循环行索引集合 5.利用XWPFTableRow对像的getCtRow().copy()方法&a…...

Oracle重建索引详解
更新:2023-05-17 18:08 一、Oracle重建索引命令 Oracle重建索引可以通过ALTER INDEX命令来完成。下面是示例代码: ALTER INDEX index_name REBUILD [PARAMETERS];其中,index_name是需要重建的索引名称,PARAMETERS是可选的重建参…...

众和策略证券开户首选:股票增持是好还是坏?大股东增持规定?
股票增持是好仍是坏? 股东增持在一定程度上反映股东对个股比较看好,大量的买单,增加了市场上的多方力气,会推动股价上涨,是一种利好消息。 一般大股东会增持可能是上市公司运营成绩较好,具有较大的发展前…...

UE4移动端最小包优化实践
移动端对于包大小有着严苛的要求,然而UE哪怕是一个空工程打出来也有90+M,本文以一个复杂的工程为例,探索怎么把包大小降低到最小。 一、工程简介 工程包含代码、插件、资源、iOS原生库工程。 二、按官方文档进行基础优化 官方文档 1、勾选Use Pak File和Create comp…...
用户管理第2节课--idea 2023.2 后端--实现基本数据库操作(操作user表) -- 自动生成
一、插件 Settings... 1.1 File -- Settings 1.2 Settings -- Plugins 1.2.1 搜索框,也可以直接搜索 1.3 Plugins -- 【输入 & 搜索】mybatis 1.3.1 插件不同功能介绍 1.3.2 翻译如下 1.4 选中 Update,更新下 1.4.1 更新中 1.4.2 Restart IDE 1…...
java开发面试:常见业务场景之单点登录SSO(JWT)、权限认证、上传数据的安全性的控制、项目中遇到的问题、日志采集(ELK)、快速定位系统的瓶颈
单点登录(SSO) 单点登录,Single Sign On(简称SSO),只需要登录一次,就可以访问所有信任的应用系统。 如果是单个tomcat服务,session可以共享,如果是多个tomcat,那么服务s…...
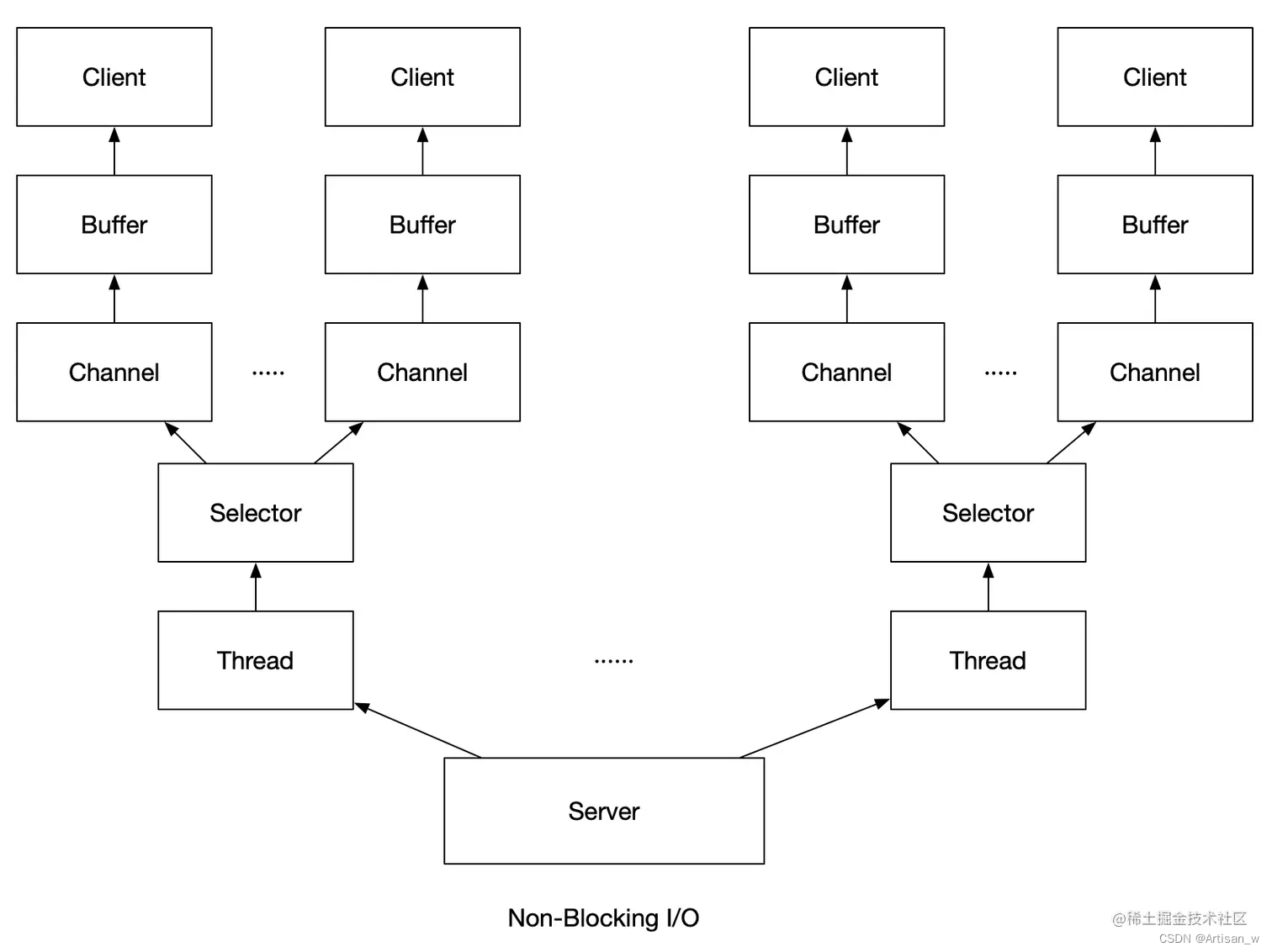
Java网络编程原理与实践--从Socket到BIO再到NIO
文章目录 Java网络编程原理与实践--从Socket到BIO再到NIOSocket基本架构Socket 基本使用简单一次发送接收客户端服务端 字节流方式简单发送接收客户端服务端 双向通信客户端服务端 多次接收消息客户端服务端 Socket写法的问题BIO简单流程BIO写法客户端服务端 BIO的问题 NIO简述…...
ARM GIC(三) gicv2架构
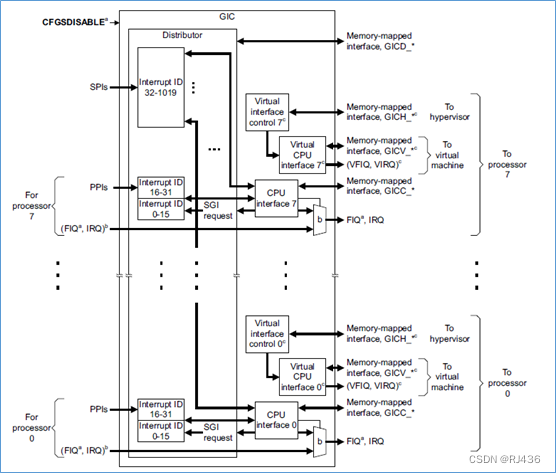
ARM的cpu,特别是cortex-A系列的CPU,目前都是多core的cpu,因此对于多core的cpu的中断管理,就不能像单core那样简单去管理,由此arm定义了GICv2架构,来支持多核cpu的中断管理 一、gicv2架构 GICv2,支持最大8个core。其框图如下图所示: 在gicv2中,gic由两个大模块组成: …...
第4章Netty第二节入门案例+channel,future,promise介绍
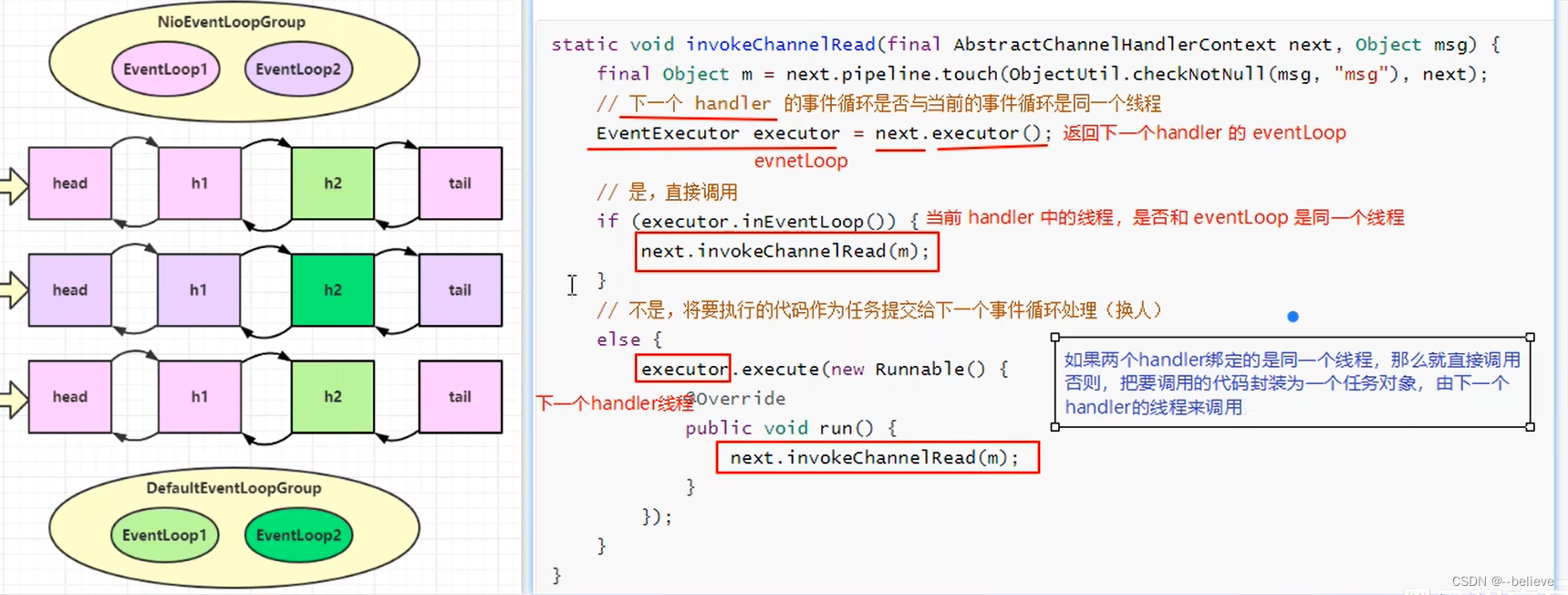
需求 开发一个简单的服务器端和客户端 客户端向服务器端发送 hello, world服务器仅接收,不返回 <dependency><groupId>io.netty</groupId><artifactId>netty-all</artifactId><version>4.1.39.Final</version> </d…...

【论文笔记】3D Gaussian Splatting for Real-Time Radiance Field Rendering
原文链接:https://arxiv.org/abs/2308.04079 1. 引言 网孔和点是最常见的3D场景表达,因其是显式的且适合基于GPU/CUDA的快速栅格化。神经辐射场(NeRF)则建立连续的场景表达便于优化,但渲染时的随机采样耗时且引入噪声…...

【生物信息学】层次聚类过程
文章目录 一、理论二、实践过程1过程2 一、理论 层次聚类是一种基于树状结构的聚类方法,它试图通过在不同层次上逐步合并或分裂数据集来构建聚类结构。这个树状结构通常被称为“树状图”(dendrogram),其中每个节点代表一个数据点或…...

变分自动编码器【03/3】:使用 Docker 和 Bash 脚本进行超参数调整
一、说明 在深入研究第 1 部分中的介绍和实现,并在第 2 部分中探索训练过程之后,我们现在将重点转向在第 3 部分中通过超参数调整来优化模型的性能。要访问本系列的完整代码,请访问我们的 GitHub 存储库在GitHub - asokraju/ImageAutoEncoder…...
KnowLM知识抽取大模型
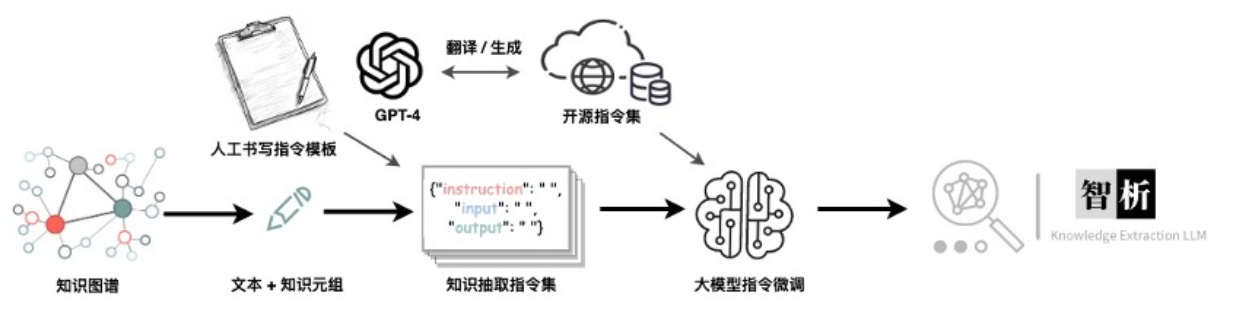
文章目录 KnowLM项目介绍KnowLM项目的动机ChatGPT存在的问题 基于LLama的知识抽取的智析大模型数据集构建及训练过程预训练数据集构建预训练训练过程指令微调数据集构建 指令微调训练过程开源的数据集及模型局限性信息抽取Prompt 部署环境配置模型下载预训练模型使用LoRA模型使…...
MySQL数据库 索引
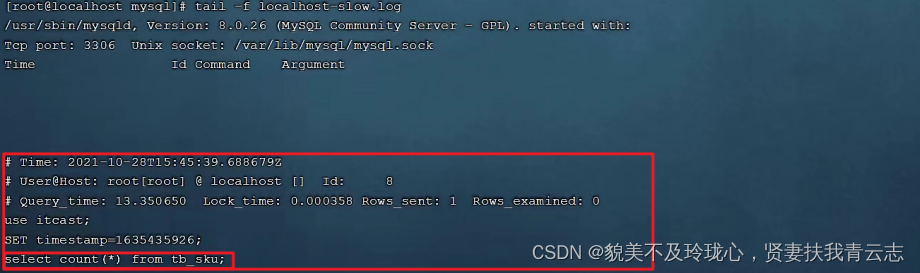
目录 索引概述 索引结构 二叉树 B-Tree BTree Hash 索引分类 索引语法 慢查询日志 索引概述 索引 (index)是帮助MySQL高效获取数据的数据结构(有序)。在数据之外,数据库系统还维护着满足特定查找算法的数据结构,这些数据结构以某种…...

ES 错误码
2xx状态码(如200)表示请求成功处理,并且不需要重试。 400状态码表示客户端发送了无效的请求,例如请求的语法有误或缺少必需的参数。在这种情况下,重试相同的请求很可能会导致相同的错误。因此,应该先检查并…...

听GPT 讲Rust源代码--src/tools(18)
File: rust/src/tools/rust-analyzer/crates/ide-ssr/src/from_comment.rs 在Rust源代码中的from_comment.rs文件位于Rust分析器(rust-analyzer)工具的ide-ssr库中,它的作用是将注释转换为Rust代码。 具体来说,该文件实现了从注…...

如何实现设备远程控制?
在工业自动化领域,设备远程控制是一项非常重要的技术。它使得设备可以在远离现场的情况下进行远程操作和维护,大大提高了设备的可用性和效率。 设备远程控制的应用场景有哪些? 远程故障排除:当设备出现故障时,工程师…...

百度侯震宇详解:大模型将如何重构云计算?
12月20日,在2023百度云智大会智算大会上,百度集团副总裁侯震宇以“大模型重构云计算”为主题发表演讲。他强调,AI原生时代,面向大模型的基础设施体系需要全面重构,为构建繁荣的AI原生生态筑牢底座。 侯震宇表示&…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...

Python 训练营打卡 Day 47
注意力热力图可视化 在day 46代码的基础上,对比不同卷积层热力图可视化的结果 import torch import torch.nn as nn import torch.optim as optim from torchvision import datasets, transforms from torch.utils.data import DataLoader import matplotlib.pypl…...

算法—栈系列
一:删除字符串中的所有相邻重复项 class Solution { public:string removeDuplicates(string s) {stack<char> st;for(int i 0; i < s.size(); i){char target s[i];if(!st.empty() && target st.top())st.pop();elsest.push(s[i]);}string ret…...
