【贪心】单源最短路径Python实现
文章目录
- @[toc]
- 问题描述
- `Dijkstra`算法
- `Dijkstra`算法的正确性
- 贪心选择性质
- 最优子结构性质
- `Dijkstra`算法应用示例
- 时间复杂性
- `Python`实现
文章目录
- @[toc]
- 问题描述
- `Dijkstra`算法
- `Dijkstra`算法的正确性
- 贪心选择性质
- 最优子结构性质
- `Dijkstra`算法应用示例
- 时间复杂性
- `Python`实现

个人主页:丷从心
系列专栏:贪心算法

问题描述
- 给定一个带权有向图 G = ( V , E ) G = (V , E) G=(V,E),其中每条边的权是非负实数,给定 V V V中的一个顶点,称为源
- 计算从源到所有其他各顶点的最短路长度
Dijkstra算法
Dijkstra算法是解单源最短路径问题的一个贪心算法- 其基本思想是,设置顶点集合 S S S,并不断地做贪心选择来扩充这个集合,一个顶点属于集合 S S S当且仅当从源到该顶点的最短路径长度已知
- 初始时, S S S中仅含有源,设 u u u是 G G G的某一个顶点,把从源到 u u u且中间只经过 S S S中顶点的路称为从源到 u u u的特殊路径,并用数组
dist记录当前每个顶点所对应的最短特殊路径长度,用列表parent[i]记录从源到顶点 i i i的最短路径上 i i i的前一个顶点 Dijkstra算法每次从 V − S V - S V−S中取出具有最短特殊路长度的顶点 u u u,将 u u u添加到 S S S中,同时对列表dist和parent做必要的修改,当dist[u] + graph[u][i] < dist[i]时,置dist[i] = dist[u] + graph[u][i],置parent[i] = u- 一旦 S S S包含了所有 V V V中顶点,
dist就记录了从源到所有其他顶点之间的最短路径长度
Dijkstra算法的正确性
贪心选择性质
Dijkstra算法所做的贪心选择是从 V − S V - S V−S中选择具有最短特殊路径的顶点 u u u,从而确定从源到 u u u的最短路径长度dist[u],从源到 u u u没有更短的其他路径- 事实上,如果存在一条从源到 u u u且长度比
dist[u]更短的路,设这条路初次走出 S S S之外到达的顶点为 x ∈ V − S x \in V - S x∈V−S,然后徘徊于 S S S内外若干次,最后离开 S S S到达 u u u

- 在这条路径上,分别记 d ( v , x ) d(v , x) d(v,x)、 d ( x , u ) d(x , u) d(x,u)和 d ( v , u ) d(v , u) d(v,u)为顶点 v v v到顶点 x x x、顶点 x x x到顶点 u u u和顶点 v v v到顶点 u u u的路长,那么
dist[x]≤ d ( v , x ) \leq d(v , x) ≤d(v,x), d ( v , x ) + d ( x , u ) = d ( v , u ) < d i s t [ u ] d(v , x) + d(x , u) = d(v , u) < dist[u] d(v,x)+d(x,u)=d(v,u)<dist[u],利用边权的非负性,可知 d ( x , u ) ≥ 0 d(x , u) \geq 0 d(x,u)≥0,从而推得dist[x]< < <dist[u],此为矛盾 - 这就证明了
dist[u]是从源到顶点 u u u的最短路径长度
最优子结构性质
- 将添加 u u u之前的 S S S称为 S ′ S^{'} S′
- 当添加了 u u u后,可能出现一条到顶点 i i i的新的特殊路

- 如果这条新特殊路是经过 S ′ S^{'} S′到达顶点 u u u,然后从 u u u经一条边直接到达顶点 i i i,则这种路的最短的长度是
dist[u]+ + +c[u][i],此时,如果dist[u]+ + +c[u][i]< < <dist[i],则算法中用dist[u]+ + +c[u][i]作为dist[i]的新值 - 如果这条新特殊路经过 S ′ S^{'} S′到达 u u u后,不是从 u u u经一条边直接到达 i i i,而是回到 S ′ S^{'} S′中某个顶点 x x x,最后才到达顶点 i i i,那么由于 x x x在 S ′ S^{'} S′中,因此 x x x比 u u u先加入 S S S,故从源到 x x x的路的长度比从源到 u u u,再从 u u u到 x x x的路的长度小,于是当前
dist[i]的值小于这条新特殊路的长度,因此,在算法中不必考虑这种路 - 由此可知,不论算法中
dist[u]的值是否有变化,它总是关于当前顶点集 S S S到顶点 u u u的最短特殊路径长度
Dijkstra算法应用示例
- 对下图中的有向图,应用
Dijkstra算法计算从源顶点 1 1 1到其他顶点间最短路径的过程如下表所示

| 迭代 | S S S | u u u | dist[2] | dist[3] | dist[4] | dist[5] |
|---|---|---|---|---|---|---|
| 初始 | { 1 } \set{1} {1} | − - − | 10 10 10 | m a x i n t maxint maxint | 30 30 30 | 100 100 100 |
| 1 1 1 | { 1 , 2 } \set{1 , 2} {1,2} | 2 2 2 | 10 10 10 | 60 60 60 | 30 30 30 | 100 100 100 |
| 2 2 2 | { 1 , 2 , 3 } \set{1 , 2 , 3} {1,2,3} | 4 4 4 | 10 10 10 | 50 50 50 | 30 30 30 | 90 90 90 |
| 3 3 3 | { 1 , 2 , 4 , 3 } \set{1 , 2 , 4 , 3} {1,2,4,3} | 3 3 3 | 10 10 10 | 50 50 50 | 30 30 30 | 60 60 60 |
| 4 4 4 | { 1 , 2 , 4 , 3 , 5 } \set{1 , 2 , 4 , 3 , 5} {1,2,4,3,5} | 5 5 5 | 10 10 10 | 50 50 50 | 30 30 30 | 60 60 60 |
时间复杂性
- 对于一个具有 n n n个顶点的带权有向图,
Dijkstra算法进行二重循环,需要 O ( n 2 ) O(n^{2}) O(n2)时间
Python实现
import sysclass Graph:def __init__(self, vertices):self.V = verticesself.graph = [[0 for _ in range(vertices)] for _ in range(vertices)]def printSolution(self, dist, parent):for v in range(self.V):path = []curr = vwhile curr != -1:path.append(curr)curr = parent[curr]path.reverse()print((v, dist[v], path))def minDistance(self, dist, sptSet):min_value = sys.maxsizemin_index = -1for v in range(self.V):if dist[v] < min_value and not sptSet[v]:min_value = dist[v]min_index = vreturn min_indexdef dijkstra(self, src):dist = [sys.maxsize] * self.Vdist[src] = 0sptSet = [False] * self.Vparent = [-1] * self.Vfor _ in range(self.V):u = self.minDistance(dist, sptSet)sptSet[u] = Truefor v in range(self.V):if self.graph[u][v] != 0 and 0 < dist[u] + self.graph[u][v] < dist[v] and not sptSet[v]:dist[v] = dist[u] + self.graph[u][v]parent[v] = uself.printSolution(dist, parent)g = Graph(9)
g.graph = [[0, 4, 0, 0, 0, 0, 0, 8, 0],[4, 0, 8, 0, 0, 0, 0, 11, 0],[0, 8, 0, 7, 0, 4, 0, 0, 2],[0, 0, 7, 0, 9, 14, 0, 0, 0],[0, 0, 0, 9, 0, 10, 0, 0, 0],[0, 0, 4, 14, 10, 0, 2, 0, 0],[0, 0, 0, 0, 0, 2, 0, 1, 6],[8, 11, 0, 0, 0, 0, 1, 0, 7],[0, 0, 2, 0, 0, 0, 6, 7, 0]]
src = 0print(f'(顶点, 以顶点 {src} 为源的最短路径长度, 最短路径)')
print('-' * 40)g.dijkstra(src)print('-' * 40)
(顶点, 以顶点 0 为源的最短路径长度, 最短路径)
----------------------------------------
(0, 0, [0])
(1, 4, [0, 1])
(2, 12, [0, 1, 2])
(3, 19, [0, 1, 2, 3])
(4, 21, [0, 7, 6, 5, 4])
(5, 11, [0, 7, 6, 5])
(6, 9, [0, 7, 6])
(7, 8, [0, 7])
(8, 14, [0, 1, 2, 8])
----------------------------------------
相关文章:

【贪心】单源最短路径Python实现
文章目录 [toc]问题描述Dijkstra算法Dijkstra算法的正确性贪心选择性质最优子结构性质 Dijkstra算法应用示例时间复杂性Python实现 个人主页:丷从心 系列专栏:贪心算法 问题描述 给定一个带权有向图 G ( V , E ) G (V , E) G(V,E),其中每…...

Spark Shell的简单使用
简介 Spark shell是一个特别适合快速开发Spark原型程序的工具,可以帮助我们熟悉Scala语言。即使你对Scala不熟悉,仍然可以使用这个工具。Spark shell使得用户可以和Spark集群交互,提交查询,这便于调试,也便于初学者使用…...

Springsecurty【2】认证连接MySQL
1.前期准备 基于Spring Initializr创建SpringBoot项目(基于SpringBoot 2.7.12版本),实现与MyBatisPlus的项目整合。分别导入:CodeGenerator和MyBatisPlusConfig。 CodeGenerator:用于MybatisPlus代码生成;…...
.Net 访问电子邮箱-LumiSoft.Net,好用
序言: 网上找了很多关于.Net如何访问电子邮箱的方法,但是大多数都达不到想要的需求,只有一些 收发邮件。因此 花了很大功夫去看 LumiSoft.Net.dll 的源码,总算做出自己想要的结果了,果然学习诗人进步。 介绍ÿ…...

谷粒商城-商品服务-新增商品功能开发(商品图片无法展示问题没有解决)
在网关配置路由 - id: member_routeuri: lb://gulimemberpredicates:- Path/api/gulimember/**filters:- RewritePath/api/(?<segment>.*),/$\{segment}并将所有逆向生成的工程调式出来 获取分类关联的品牌 例如:手机(分类)-> 品…...

Open3D 点云数据处理基础(Python版)
Open3D 点云数据处理基础(Python版) 文章目录 1 概述 2 安装 2.1 PyCharm 与 Python 安装 2.3 Anaconda 安装 2.4 Open3D 0.13.0 安装 2.5 新建一个 Python 项目 3 点云读写 4 点云可视化 2.1 可视化单个点云 2.2 同一窗口可视化多个点云 2.3…...

使用vue-qr,报错in ./node_modules/vue-qr/dist/vue-qr.js
找到node_modules—>vue-qr/dist/vue-qr.js文件,搜…e,将…去掉,然后重新运行项目。...

百川2大模型微调问题解决
之前用https://github.com/FlagAlpha/Llama2-Chinese微调过几个模型,总体来说llama2的生态还是比较好的,过程很顺利。微调百川2就没那么顺利了,所以简单做个记录 1. 数据准备,我的数据是单轮对话,之前微调llama2已经按…...

MySQL的事务-原子性
MySQL的事务处理具有ACID的特性,即原子性(Atomicity)、一致性(Consistency)、隔离性(Isolation)和持久性(Durability)。 1. 原子性指的是事务中所有操作都是原子性的,要…...

D3839|完全背包
完全背包: 首先01背包的滚动数组中的解法是内嵌的循环是从大到小遍历,为了保证每个物品仅被添加一次。 for(int i 0; i < weight.size(); i) { // 遍历物品for(int j bagWeight; j > weight[i]; j--) { // 遍历背包容量dp[j] max(dp[j], dp[j…...
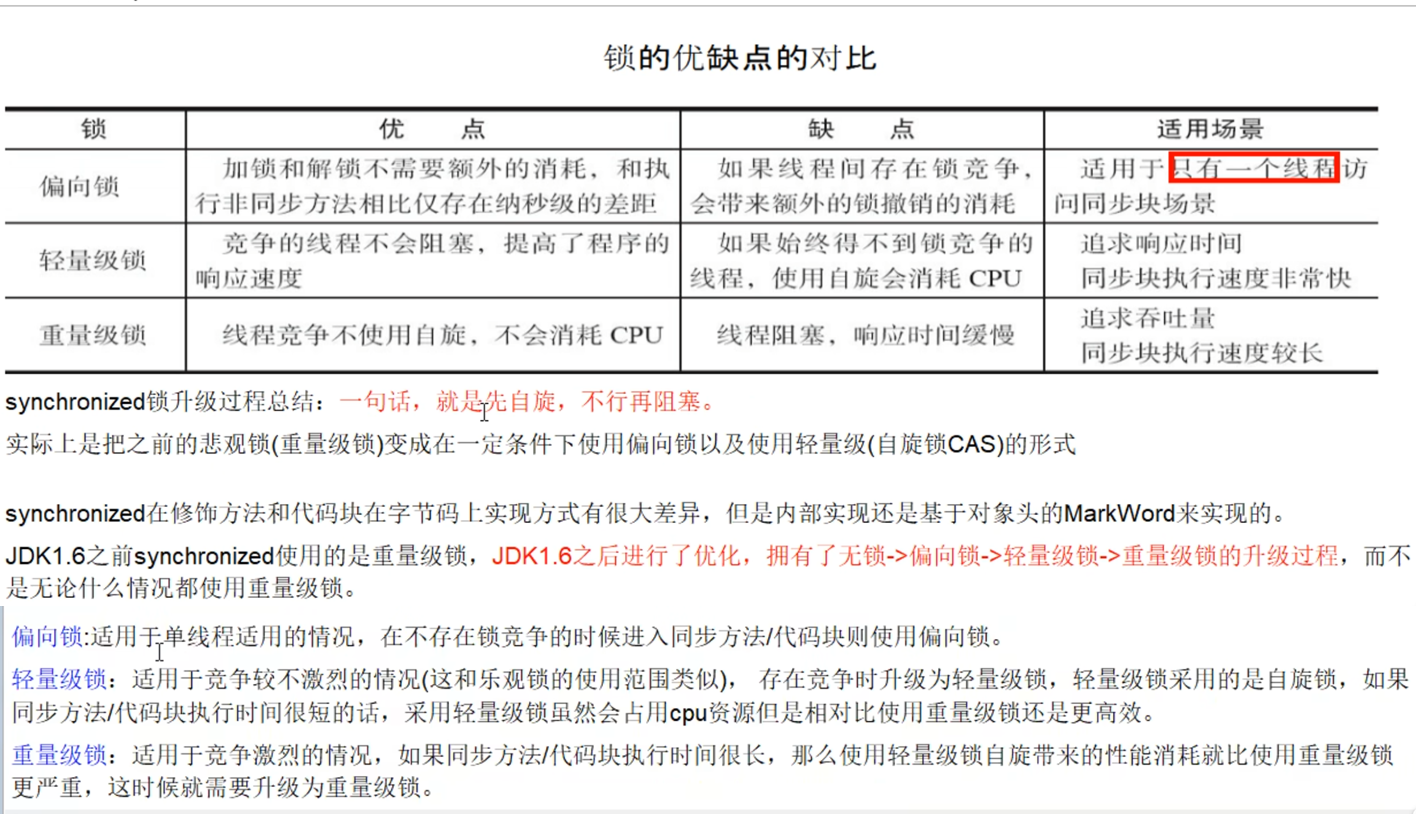
Java之Synchronized与锁升级
Synchronized与锁升级 一、概述 在多线程并发编程中 synchronized 一直是元老级角色,很多人都会称呼它为重量级锁。但是,随着 Java SE 1.6 对 synchronized 进行了各种优化之后,有些情况下它就并不那么重了。 本文详细介绍 Java SE 1.6 中为…...

kitex出现:open conf/test/conf.yaml: no such file or directory
open conf/test/conf.yaml: no such file or directory https://github.com/cloudwego/cwgo/issues/120 https://github.com/cloudwego/cwgo/issues/29 在使用Kitex生成的代码中,单元测试时回报错,如标题所示。出现该错的原因是,biz/servic…...

sql server多表查询
查询目标 现在有学生表和学生选课信息表,stu和stuSelect,stu中包含学生用户名、名字,stuSelect表中包含学生用户名,所选课程名 学生表: nameusername李明Li Ming李华Li Hua 学生选课表: usernameCourse…...
如何利用PPT绘图并导出清晰图片
在写论文的过程中,免不了需要绘图,但是visio等软件绘图没有在ppt上绘图比较熟练,尤其流程图结构图. 但是ppt导出的图片也不够清晰,默认分辨率是96dpi,而杂志投稿一般要求至300dpi。解决办法如下: 1.打开注…...

1.倒排索引 2.逻辑斯提回归算法
1.倒排索引 https://help.aliyun.com/zh/open-search/retrieval-engine-edition/introduction-to-inverted-indexes 倒排索引(Inverted Index)是一种数据结构,用于快速查找包含某个特定词或词语的文档。它主要用于全文搜索引擎等应用&#…...
Kafka消费者组
消费者总体工作流程 Consumer Group(CG):消费者组,由多个consumer组成。形成一个消费者组的条件,是所有消费者的groupid相同。 • 消费者组内每个消费者负责消费不同分区的数据,一个分区只能由一个组内消费…...

四. 基于环视Camera的BEV感知算法-BEVDepth
目录 前言0. 简述1. 算法动机&开创性思路2. 主体结构3. 损失函数4. 性能对比总结下载链接参考 前言 自动驾驶之心推出的《国内首个BVE感知全栈系列学习教程》,链接。记录下个人学习笔记,仅供自己参考 本次课程我们来学习下课程第四章——基于环视Cam…...
——使用docker compose安装mysql)
CentOS系统环境搭建(二十五)——使用docker compose安装mysql
centos系统环境搭建专栏🔗点击跳转 文章目录 使用docker compose安装mysqlMySQL81.新建文件夹2.创建docker-compose.yaml3.创建my.cnf4.mysql容器的启动和关闭 MySQL5.71.新建文件夹2.创建docker-compose.yaml3.创建my.cnf4.mysql容器的启动和关闭 使用docker comp…...
协作机器人(Collaborative-Robot)安全碰撞的速度与接触力
协作机器人(Collaborative-Robot)的安全碰撞速度和接触力是一个非常重要的安全指标。在设计和使用协作机器人时,必须确保其与人类或其他物体的碰撞不会对人员造成伤害。 对于协作机器人的安全碰撞速度,一般会设定一个上限值&…...

第11章 GUI Page400~402 步骤二 画直线
运行效果: 源代码: /**************************************************************** Name: wxMyPainterApp.h* Purpose: Defines Application Class* Author: yanzhenxi (3065598272qq.com)* Created: 2023-12-21* Copyright: yanzhen…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...

如何应对敏捷转型中的团队阻力
应对敏捷转型中的团队阻力需要明确沟通敏捷转型目的、提升团队参与感、提供充分的培训与支持、逐步推进敏捷实践、建立清晰的奖励和反馈机制。其中,明确沟通敏捷转型目的尤为关键,团队成员只有清晰理解转型背后的原因和利益,才能降低对变化的…...

AxureRP-Pro-Beta-Setup_114413.exe (6.0.0.2887)
Name:3ddown Serial:FiCGEezgdGoYILo8U/2MFyCWj0jZoJc/sziRRj2/ENvtEq7w1RH97k5MWctqVHA 注册用户名:Axure 序列号:8t3Yk/zu4cX601/seX6wBZgYRVj/lkC2PICCdO4sFKCCLx8mcCnccoylVb40lP...

基于开源AI智能名片链动2 + 1模式S2B2C商城小程序的沉浸式体验营销研究
摘要:在消费市场竞争日益激烈的当下,传统体验营销方式存在诸多局限。本文聚焦开源AI智能名片链动2 1模式S2B2C商城小程序,探讨其在沉浸式体验营销中的应用。通过对比传统品鉴、工厂参观等初级体验方式,分析沉浸式体验的优势与价值…...
