当前位置： 首页 > news >正文

幺模矩阵-线性规划的整数解特性

news 2026/2/10 17:51:17

百度百科:幺模矩阵
在这里插入图片描述
在线性规划问题中，如果A为幺模矩阵，那么该问题具有最优整数解特性。也就是说使用单纯形法进行求解，得到的解即为整数解。无需再特定使用整数规划方法。
m i n c T x s . t . { A x ≥ b x ≥ 0 \begin{align*} min \quad & \mathbf{c}^T \mathbf{x} \\ s.t. \quad & \begin{cases} \mathbf{Ax} \geq \mathbf{b} \\ \mathbf{x} \geq \mathbf{0} \end{cases} \\ \end{align*} mins.t.​cTx{Ax≥bx≥0​​
在实际应用中，例如网络流问题、匹配问题和覆盖问题等，在问题的线性表示中，经常出现幺模矩阵作为约束矩阵。

相关文章：

幺模矩阵-线性规划的整数解特性

百度百科:幺模矩阵 在线性规划问题中，如果A为幺模矩阵，那么该问题具有最优整数解特性。也就是说使用单纯形法进行求解，得到的解即为整数解。无需再特定使用整数规划方法。 m i n c T x s . t . { A x ≥ b x ≥ 0 \begin{align*} min \quad…...

编程日记 2023/12/25 12:13:06

数据分析思维

Why&What 数据分析是为了驱动决策赋能业务。在数据分析过程中需要对目标进行拆解量化，如何拆解量化目标便是数据分析思维。 在任务拆解过程中使用的软件、统计模型、分析方法等为分析工具和手段，如何在恰当的场景合理的使用这些工具、模型、方法、手…...

编程日记 2023/12/25 12:03:58

C++ boost planner_cond_.wait(lock) 报错1225

1.如下程序段 boost unique_lock doesn’t own the mutex: Operation not permitted 问题： 其中makePlan是一个线程。这里的unlock导致错误这个报错 boost unique_lock doesn’t own the mutex: Operation not permitted bool navigation::makePlan(){ //cv::named…...

编程日记 2023/12/25 12:00:56

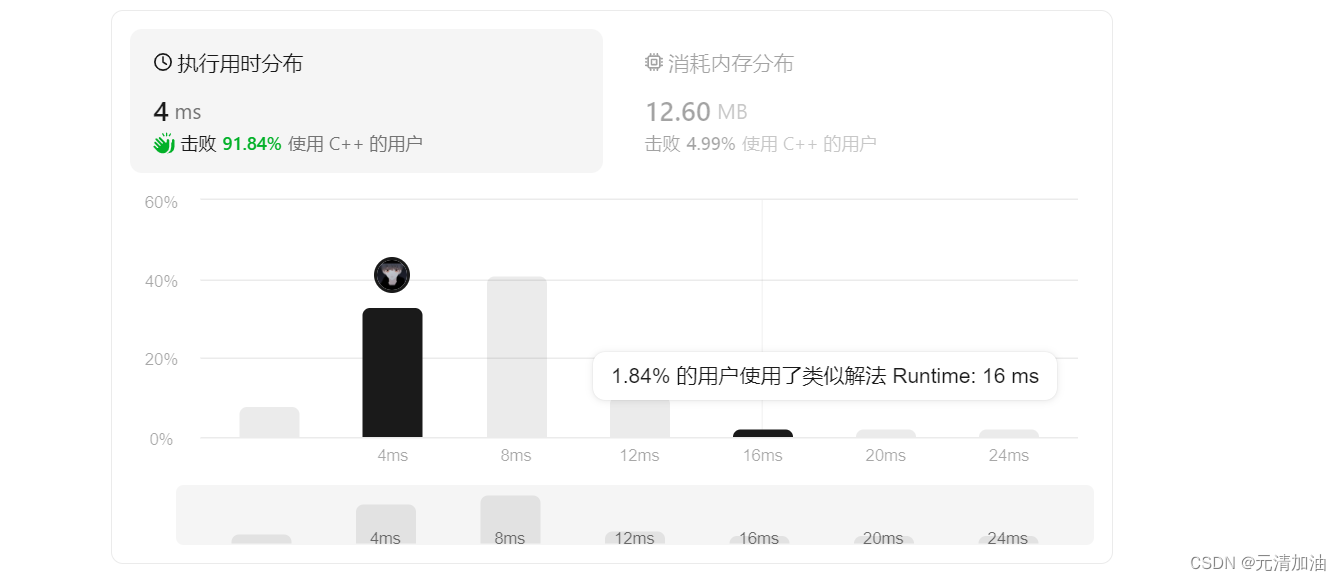
LeetCode刷题--- 字母大小写全排列

个人主页：元清加油_【C】,【C语言】,【数据结构与算法】-CSDN博客 个人专栏 力扣递归算法题 http://t.csdnimg.cn/yUl2I 【C】 http://t.csdnimg.cn/6AbpV 数据结构与算法 http://t.csdnimg.cn/hKh2l 前言：这个专栏主要讲述递归递归、搜索与回…...

编程日记 2023/12/25 11:59:55

165. 小猫爬山（DFS之剪枝与优化）

165. 小猫爬山 - AcWing题库 翰翰和达达饲养了 N 只小猫&#xff0c;这天&#xff0c;小猫们要去爬山。 经历了千辛万苦&#xff0c;小猫们终于爬上了山顶&#xff0c;但是疲倦的它们再也不想徒步走下山了&#xff08;呜咕>_<&#xff09;。 翰翰和达达只好花钱让它们…...

编程日记 2023/12/25 11:58:54

【Linux系统基础】（6）在Linux上大数据NoSQL数据库HBase集群部署、分布式内存计算Spark环境及Flink环境部署详细教程

大数据NoSQL数据库HBase集群部署 简介 HBase 是一种分布式、可扩展、支持海量数据存储的 NoSQL 数据库。 和Redis一样&#xff0c;HBase是一款KeyValue型存储的数据库。 不过和Redis设计方向不同 Redis设计为少量数据&#xff0c;超快检索HBase设计为海量数据&#xff0c;…...

编程日记 2023/12/25 11:57:53

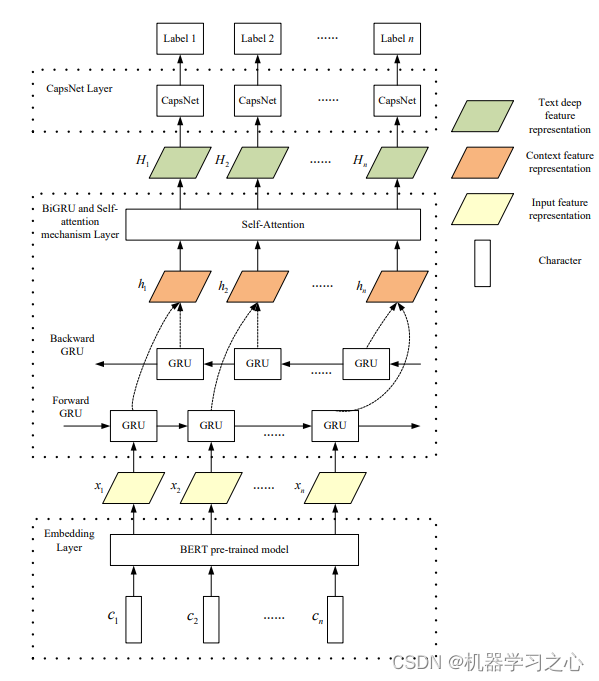
多维时序 | MATLAB实CNN-BiGRU-Mutilhead-Attention卷积网络结合双向门控循环单元网络融合多头注意力机制多变量时间序列预测

多维时序 | MATLAB实现CNN-BiGRU-Mutilhead-Attention卷积网络结合双向门控循环单元网络融合多头注意力机制多变量时间序列预测 目录 多维时序 | MATLAB实现CNN-BiGRU-Mutilhead-Attention卷积网络结合双向门控循环单元网络融合多头注意力机制多变量时间序列预测预测效果基本介…...

编程日记 2023/12/25 11:56:52

vs快捷键

ctrlMo 折叠代码块 ctrlML 打开代码块...

编程日记 2023/12/25 11:55:51

linux 内核时间计量方法

定时器中断由系统定时硬件以规律地间隔产生; 这个间隔在启动时由内核根据 HZ 值来编 程, HZ 是一个体系依赖的值, 在 <linux/param.h>中定义或者它所包含的一个子平台文 件中. 在发布的内核源码中的缺省值在真实硬件上从 50 到 1200 嘀哒每秒, 在软件模拟 器中往下到 24.…...

编程日记 2023/12/25 11:53:50

循环神经网络中的梯度消失或梯度爆炸问题产生原因分析（二）

上一篇中讨论了一般性的原则&#xff0c;这里我们具体讨论通过时间反向传播&#xff08;backpropagation through time&#xff0c;BPTT&#xff09;的细节。我们将展示目标函数对于所有模型参数的梯度计算方法。 出于简单的目的&#xff0c;我们以一个没有偏置参数的循环神经…...

编程日记 2023/12/25 11:50:47

JWT signature does not match locally computed signature

1. 问题背景 最近在协助团队小盆友调试一个验签问题&#xff0c;结果还“节外生枝”了&#xff0c;原来不是签名过程的问题&#xff0c;是token的问题。 当你看到“JWT signature does not match locally computed signature. JWT validity cannot be asserted and should not…...

编程日记 2023/12/25 11:48:45

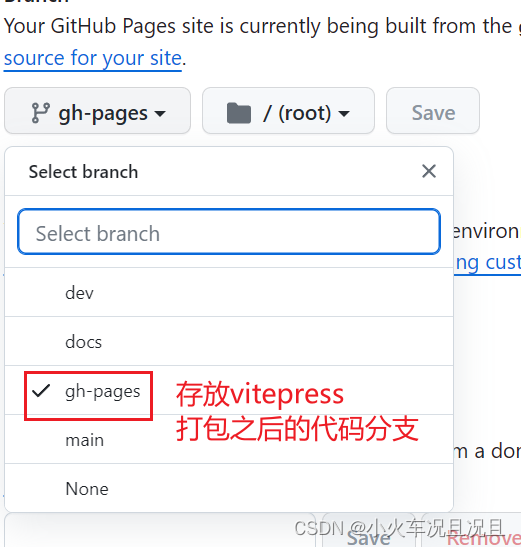
vitepress项目使用github的action自动部署到github-pages中，理论上可以通用所有

使用github的action自动部署到github-pages中 创建部署的deploy.yml文件&#xff0c;在项目的根目录下面 .github\workflows\deploy.yml 完整的代码&#xff1a;使用的是pnpm进行依赖安装。 name: 部署VitePresson:push:branches:- docs # 这段是在推送到 docs 分支时触发该…...

编程日记 2023/12/25 11:45:42

Python爬虫---解析---JSONPath

Xpath可以解析本地文件和服务器响应的文件&#xff0c;JSONPath只能解析本地文件 1. 安装jsonpath&#xff1a;pip install jsonpath 注意&#xff1a;需要安装在python解释器相同的位置,例如&#xff1a;D:\Program Files\Python3.11.4\Scripts 2. 使用步骤 2.1 导入&…...

编程日记 2023/12/25 11:44:41

路由器介绍和命令操作

先来回顾一下上次的内容&#xff1a; ip地址就是由32位二进制数组 二进位数就是只有数字0和1组成 网络位&#xff1a;类似于区号&#xff0c;表示区域作用 主机位&#xff1a;类似于号码&#xff0c;表示区域中编号 网络名称&#xff1a;网络位不变&#xff0c;主机位全为0 …...

编程日记 2023/12/25 11:43:40

Hadoop——分布式计算

一、分布式计算概述 1. 什么是计算、分布式计算？ 计算：对数据进行处理，使用统计分析等手段得到需要的结果分布式计算：多台服务器协同工作，共同完成一个计算任务2. 分布式计算常见的2种工作模式分散->汇总 （MapReduce就是这种模式）将数据分片，多台服务器各自负责一…...

编程日记 2023/12/25 11:40:37

LaTeX引用参考文献 | Texstudio引用参考文献

图片版教程&#xff1a; 文字版教程&#xff1a; ref.bib里面写参考的文献&#xff0c;ref.bib和document.tex要挨着放&#xff0c;同一个目录里面. 解析一下bib文件格式&#xff1a;aboyeji2023effect是引用文献的关键字&#xff0c;需要在正文document.tex里面使用\cite指令…...

编程日记 2023/12/25 11:39:37

如何在Go中使用模板

引言 您是否需要以格式良好的输出、文本报告或HTML页面呈现一些数据?你可以使用Go模板来做到这一点。任何Go程序都可以使用text/template或html/template包(两者都包含在Go标准库中)来整齐地显示数据。 这两个包都允许你编写文本模板并将数据传递给它们，以按你喜欢的格式呈…...

编程日记 2023/12/25 11:37:35

云原生之深入解析基于FunctionGraph在Serverless领域的FinOps的探索和实践

一、背景 Serverless 精确到毫秒级的按用付费模式使得用户不再需要为资源的空闲时间付费。然而&#xff0c;对于给定的某个应用函数&#xff0c;由于影响其计费成本的因素并不唯一&#xff0c;使得用户对函数运行期间的总计费进行精确的事先估计变成了一项困难的工作。以传统云…...

编程日记 2023/12/25 11:36:34

电子电器架构（E/E）演化 —— 主流主机厂域集中架构概述

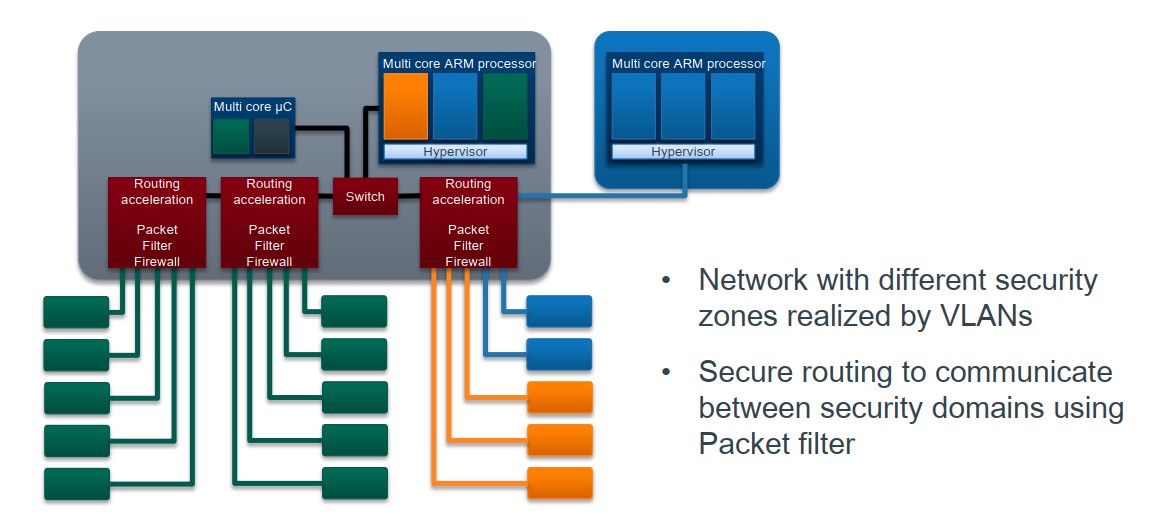
电子电器架构（E/E）演化 —— 主流主机厂域集中架构概述 我是穿拖鞋的汉子，魔都中坚持长期主义的汽车电子工程师。 老规矩，分享一段喜欢的文字，避免自己成为高知识低文化的工程师： 屏蔽力是信息过载时代一个人的特殊竞争力，任何消耗你的人和事，多看一眼都是你的不对。…...

编程日记 2023/12/25 11:33:32

Python常用的几个函数

print()函数&#xff1a;用于打印输出信息到控制台。 input()函数&#xff1a;用于从控制台获取用户输入。 len()函数&#xff1a;用于获取字符串、列表、元组、字典等对象的长度。 range()函数&#xff1a;用于生成一个整数序列&#xff0c;常用于循环中。 type()函数&…...

编程日记 2023/12/25 11:31:28

网络编程（Modbus进阶）

思维导图 Modbus RTU&#xff08;先学一点理论&#xff09; 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议&#xff0c;由 Modicon 公司&#xff08;现施耐德电气&#xff09;于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

编程新知 2026/2/9 2:42:51

PPT|230页| 制造集团企业供应链端到端的数字化解决方案：从需求到结算的全链路业务闭环构建

制造业采购供应链管理是企业运营的核心环节&#xff0c;供应链协同管理在供应链上下游企业之间建立紧密的合作关系&#xff0c;通过信息共享、资源整合、业务协同等方式&#xff0c;实现供应链的全面管理和优化&#xff0c;提高供应链的效率和透明度&#xff0c;降低供应链的成…...

编程新知 2026/1/30 22:07:56

（二）原型模式

原型的功能是将一个已经存在的对象作为源目标，其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现，忽略对象创建过程中的其它细节。 📌 核心特点： 避免重复初…...

编程新知 2026/2/10 15:49:06

基于matlab策略迭代和值迭代法的动态规划

经典的基于策略迭代和值迭代法的动态规划matlab代码&#xff0c;实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

编程新知 2025/12/7 23:28:25

代码随想录刷题day30

1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币&#xff0c;另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额&#xff0c;返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

编程新知 2025/10/4 6:30:56

在树莓派上添加音频输入设备的几种方法

在树莓派上添加音频输入设备可以通过以下步骤完成&#xff0c;具体方法取决于设备类型&#xff08;如USB麦克风、3.5mm接口麦克风或HDMI音频输入&#xff09;。以下是详细指南&#xff1a; 1. 连接音频输入设备 USB麦克风/声卡&#xff1a;直接插入树莓派的USB接口。3.5mm麦克…...

编程新知 2025/11/22 14:54:34

Python爬虫实战：研究Restkit库相关技术

1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代，互联网上存在着海量的有价值数据。如何高效地采集这些数据并将其应用于实际业务中，成为了许多企业和开发者关注的焦点。网络爬虫技术作为一种自动化的数据采集工具，可以帮助我们从网页中提取所需的信息。而 RESTful API …...

编程新知 2025/12/28 16:59:52

深度解析：etcd 在 Milvus 向量数据库中的关键作用

目录 &#x1f680; 深度解析&#xff1a;etcd 在 Milvus 向量数据库中的关键作用 &#x1f4a1; 什么是 etcd&#xff1f; &#x1f9e0; Milvus 架构简介 &#x1f4e6; etcd 在 Milvus 中的核心作用 &#x1f527; 实际工作流程示意 ⚠️ 如果 etcd 出现问题会怎样&am…...

编程新知 2025/10/31 3:16:51

大模型真的像人一样“思考”和“理解”吗？​

Yann LeCun 新研究的核心探讨&#xff1a;大语言模型&#xff08;LLM&#xff09;的“理解”和“思考”方式与人类认知的根本差异。 核心问题&#xff1a;大模型真的像人一样“思考”和“理解”吗&#xff1f; 人类的思考方式&#xff1a; 你的大脑是个超级整理师。面对海量信…...

编程新知 2025/11/28 20:02:50

二叉树-144.二叉树的前序遍历-力扣(LeetCode)

一、题目解析 对于递归方法的前序遍历十分简单&#xff0c;但对于一位合格的程序猿而言&#xff0c;需要掌握将递归转化为非递归的能力&#xff0c;毕竟递归调用的时候会调用大量的栈帧&#xff0c;存在栈溢出风险。 二、算法原理 递归调用本质是系统建立栈帧&#xff0c;而非…...

编程新知 2026/2/5 3:46:26