河南工程学院第六届程序设计竞赛-A组-题解
更好的阅读体验 \color{red}{更好的阅读体验} 更好的阅读体验
远古时期的签到题
原题链接
描述:
远古时期奇妙的事情…
远古时期有一个比赛,里面有这样一道签到题:
- 给定一个正整数 N N N
- 求这个整数转化为二进制后的数有多少位是 0 0 0。
输入格式:
共一行,一个正整数 N N N。
输出格式:
共一行,一个整数,表示 N N N 转化为二进制后数位是 0 0 0 的个数。
数据范围:
0 ≤ N ≤ 1 × 1 0 18 0\le N \le 1\times10^{18} 0≤N≤1×1018。
样例输入:
5
样例输出:
1
提示:
对于样例, 5 5 5 的二进制表示为 101 101 101,只有一个 0 0 0。
思想1:
- 签到题。
- 位运算。
代码:
#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <sstream>
#include <vector>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <unordered_map>
#include <unordered_set>
#include <stdio.h>using namespace std;#define IOS ios::sync_with_stdio(false),cin.tie(nullptr),cout.tie(nullptr)
#define re register
#define fi first
#define se second
#define endl '\n'typedef long long LL;
typedef pair<int, int> PII;
typedef pair<LL, LL> PLL;const int N = 1e6 + 3;
const int M = 1e7 + 10;
const int INF = 0x3f3f3f3f, mod = 1e9 + 7;
const double eps = 1e-6, PI = acos(-1);void solve(){LL n; cin >> n;int cnt = 0;if(n == 0){cout << 1 << endl;return ;}while(n){cnt += (n & 1 == 1 ? 0 : 1);n >>= 1;}cout << cnt << endl;
}int main(){IOS;int _ = 1;// cin >> _;while(_ --){solve();}return 0;}
思想2:
- 进制转换。
代码
#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <sstream>
#include <vector>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <unordered_map>
#include <unordered_set>using namespace std;#define IOS ios::sync_with_stdio(false),cin.tie(nullptr),cout.tie(nullptr)
#define re register
#define fi first
#define se second
#define endl '\n'typedef long long LL;
typedef pair<int, int> PII;
typedef pair<LL, LL> PLL;const int N = 1e6 + 3;
const int INF = 0x3f3f3f3f, mod = 1e9 + 7;
const double eps = 1e-6, PI = acos(-1);//将long long类型的x从10进制转换为p进制,返回值类型为string类型
string to_p(long long x, long long p){ string ans;if(x == 0) return "0";while(x){long long k = x % p; char c;if(k < 10) c = k + '0';else c = k + 'A' - 10;ans = c + ans;x /= p;}return ans;
}//将string类型的x从p进制转换为10进制,返回值为long long类型
long long to_x(string x, long long p){long long ans = 0;for(int i = 0; i < x .size(); i ++){long long k = 0;if(x[i] >= '0' && x[i] <= '9') k = x[i] - '0';else k = x[i] - 'A' + 10;ans = ans * p + k;}return ans;
}//将string类型的x从r进制转为p进制,返回值为string类型
string r_to_p(string x, long long r, long long p){return to_p(to_x(x, r), p);
}void solve(){string s; cin >> s;string p = r_to_p(s, (LL)10, (LL)2);int cnt = 0;for(int i = 0; i < p.size(); i ++){if(p[i] == '0') cnt ++;}cout << cnt << endl;
}int main(){IOS;int _ = 1;// cin >> _;while(_ --){solve();}return 0;}
开根
原题链接
描述:
H F HF HF 告诉 L Y S LYS LYS 说:“我最近学习了二分开根号!!!” L Y S LYS LYS 说:“那我给你出一个开五次方根的题目!” H F HF HF 感觉太简单了,就来找你们解决这个问题。
输入格式;
一行,输入一个整数 n n n
输出格式:
一行,一个浮点数,表示 n n n 开五次方根的结果。(保留六位小数)
数据范围:
1 ≤ n ≤ 1 0 6 1 \le n \le 10^6 1≤n≤106
样例输入:
32
样例输出:
2.000000
思想:
- 作为一个名副其实的签到题,也不必多说
- 直接用pow函数就可以做了
- 不过有实力的人想用二分也不是不行hh!
代码:
#include<bits/stdc++.h>
using namespace std;
int main()
{int n;cin>>n;printf("%.6lf",pow(n,0.2));
}
#include<bits/stdc++.h>
using namespace std;
int main()
{int n;cin>>n;double l=-1000000,r=1000000;while(r-l>=1e-8){double mid=(l+r)/2;if(mid*mid*mid*mid*mid>=n){r=mid;}elsel=mid;}printf("%.6lf",l);
}
乖乖♂站好
原题链接
描述:
现在有人组队要来撅我们的野兽仙贝,可是人实在是太多了,野兽仙贝想要这些人排好队,于是他喊道“乖乖♂站好!”

已知在这 N N N 个人编号为 1 ∼ N 1\sim N 1∼N,编号为 i i i 的人身高为 h i h_i hi,将这些人按照身高由低到高进行排序,若有相同身高的人,其编号小的排在前面。请你按顺序输出当前排好序的队伍里当前位置所站的人的编号。
输入格式:
第一行,一个整数 N N N,代表总人数。
接下来 N N N 个整数 h h h,第 i i i 个整数 h i h_i hi 代表编号为 i i i 的人的身高。
输出格式:
共一行, N N N 个整数,表示当前位置上的人的编号,每个编号之间空一格。
数据范围:
1 ≤ N ≤ 1 × 1 0 6 , 1 ≤ h ≤ 2 1\le N \le 1\times 10^6,1\le h\le 2 1≤N≤1×106,1≤h≤2。
样例输入:
5
1.1 1.8 1.2 1.1 1.3
样例输出:
1 4 3 5 2
思想:
- 签到题。
- 结构体排序。
- 可能会卡时间,建议
scanf()
代码:
#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <sstream>
#include <vector>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <unordered_map>
#include <unordered_set>
#include <stdio.h>using namespace std;#define IOS ios::sync_with_stdio(false),cin.tie(nullptr),cout.tie(nullptr)
#define re register
#define fi first
#define se second
#define endl '\n'typedef long long LL;
typedef pair<int, int> PII;
typedef pair<LL, LL> PLL;const int N = 1e6 + 3;
const int M = 1e7 + 10;
const int INF = 0x3f3f3f3f, mod = 1e9 + 7;
const double eps = 1e-6, PI = acos(-1);struct people{int x;double h;
}p[N];bool cmp(people &p1, people &p2){if(p1.h == p2.h) return p1.x < p2.x;return p1.h < p2.h;
}void solve(){int n; cin >> n;for(int i = 0; i < n; i ++){double l; cin >> l;p[i] = {i + 1, l};}sort(p, p + n, cmp);for(int i = 0; i < n; i ++) cout << p[i].x << ' ';
}int main(){IOS;int _ = 1;// cin >> _;while(_ --){solve();}return 0;}
毒瘤题
原题链接
描述:
H F HF HF 与 L Y S LYS LYS 在交流一些灰常复杂的问题,不是别的,就是组合计数问题。在经历了两年半的历练, L Y S LYS LYS 感觉自己的组合计数已经炉火纯青辣,于是 H F HF HF 打算给他加点难度来考验一下 L Y S LYS LYS。

L Y S LYS LYS 的脑瓜转动速度已经大幅超越计算机,他自言说:“我要更难的!组合数太小了(众所周知,后面的组合数灰常的大),我要你在 n n n 大于 24 24 24 时的组合数结果再乘上 7 7 7 的 17 17 17 次方,这样才符合我的计算能力!!!”我奈何不过 L Y S LYS LYS,只能修改题目!
给定 n , m n,m n,m,代表从 n n n 个物品当中选取 m m m 个物品总共有多少种方案。当 n n n 大于 24 24 24 时答案再乘上 7 7 7 的 17 17 17 次方。(由于数据范围过大,答案请对 40353607 40353607 40353607 取余。)
输入格式:
一行,输入两个数,分别为 n n n, m m m
输出格式:
输出一个数,为取余后最终答案
数据范围:
1 ≤ m ≤ n ≤ 1 0 9 1\le m \le n \le 10^9 1≤m≤n≤109
样例输入:
8 4
样例输出:
70
思想:
- 作为一个毒瘤题,那必须要有毒瘤的样子
- 本题考的不难,就是对数字的敏感程度,毕竟这种题目在比赛当中还是比较常见的。
- 题目的意思就是求组合数,童叟无欺,只不过就是数据很大,但是观察仔细的话,会发现乘的那个数和取余的那个数是有关系的
- 什么算法也不用,杨辉三角,递归,公式法,lucas 定理都可以来做这个题目,因为当 n 大于 24 24 24 的时候全是 0 0 0
代码:
#include <bits/stdc++.h>
using namespace std;
using ll = long long;int C(int n, int m) {if (n < m) return 0;if (!m) return 1;return (C(n - 1, m - 1) + C(n - 1, m)) % 40353607;
}int main(){ios::sync_with_stdio(false);cin.tie(0);int n, m; cin >> n >> m;if (n > 24) cout << 0 << endl;else cout << C(n, m) << endl;return 0;
}
LYS 拿 HF 的U盘
原题链接
描述:
众嗦粥汁, H F HF HF 的 U U U 盘里存着许多宝贵的学习资料, L Y S LYS LYS 的学习资料不够了,于是他去找万能 H F HF HF 大佬,可是 H F HF HF 大佬的 U U U 盘实在太多了,这让 L Y S LYS LYS 很是震惊。为了安全起见,在拿 U U U 盘时规定了他只能拿有保护套的 U U U 盘。
已知 H F HF HF 有 N N N 个 U U U 盘,编号为 1 ∼ N 1\sim N 1∼N, L Y S LYS LYS 可以对这 N N N 个 U U U 盘进行如下操作:
- 若第 i i i 个 U U U 盘有保护套,那么他可以将该 U U U 盘的保护套取下,套给第 i − 1 i-1 i−1 个 U U U 盘。
- 原本无保护套的 U U U 盘接收其他 U U U 盘的保护套后不能再执行上述操作。
- 原本有保护套的 U U U 盘最多执行一次上述操作,执行上述操作一次后仍可以接收其他 U U U 盘的保护套。
现在给定你一个长度为 N N N 且只包含 0 0 0 和 1 1 1 的字符串 S S S,其中 S i S_i Si 为 1 1 1 时表示编号为 i i i 的 U U U 盘有保护套,反之则无,第 i i i 个 U U U 盘的含有空间大小为 G i G_i Gi 的学习资料。由于 L Y S LYS LYS 只能拿走有保护套的 U U U 盘,他想知道对这些 U U U 盘进行如上可行操作之后,可取走的 U U U 盘学习资料的空间之和最大为多少!!!
输入格式:
第一行,一个整数 N N N,表示 U U U 盘数量。
第二行,一个长度为 N N N 的只包含 0 0 0 和 1 1 1 的字符串 S S S。
第三行,共 N N N 个整数 G G G,第 i i i 个整数 G i G_i Gi 表示编号为 i i i 的 U U U 盘所含学习资料的空间大小。
输出格式:
共一行,输出可取走的 U U U 盘学习资料的空间之和的最大值。
数据范围:
1 ≤ N ≤ 1 × 1 0 6 , 1 ≤ G ≤ 1 × 1 0 9 1\le N \le 1\times 10^6,1\le G\le 1\times 10^9 1≤N≤1×106,1≤G≤1×109。
样例输入:
5
10011
1 5 4 3 2
样例输出:
8
提示:
对于样例,我们将编号为 4 4 4 的 U U U 盘的保护套取下,套给编号 3 3 3,然后将编号为 5 5 5 的 U U U 盘保护套取下,套给编号 4 4 4。编号 3 3 3 的 U U U 盘原本无保护套,所以不能执行操作。最终可以拿走编号为 1 , 3 , 4 1,3,4 1,3,4 的 U U U 盘,使得学习资料空间总和最大为 8 8 8。
思想:
- 贪心。
- 对于某个连续的 1 1 1 的区间 ( i , j ) (i,j) (i,j),我们可以移动的保护套范围在 ( i − 1 , j ) (i-1,j) (i−1,j)。
- 那么在区间 ( i − 1 , j ) (i-1,j) (i−1,j) 中必然存在一个 U U U 盘没有保护套。
- 故需要将区间 ( i − 1 , j ) (i-1,j) (i−1,j) 中所含学习资料空间最少的 U U U 盘的保护套移除,提供给没有保护套的 U U U 盘。
代码:
#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <sstream>
#include <vector>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <unordered_map>
#include <unordered_set>using namespace std;#define IOS ios::sync_with_stdio(false),cin.tie(nullptr),cout.tie(nullptr)
#define re register
#define fi first
#define se second
#define endl '\n'typedef long long LL;
typedef pair<int, int> PII;
typedef pair<LL, LL> PLL;const int N = 1e6 + 3;
const int INF = 0x3f3f3f3f, mod = 1e9 + 7;
const double eps = 1e-6, PI = acos(-1);int a[N];void solve(){int n; cin >> n;string s; cin >> s;for(int i = 0; i < n; i ++) cin >> a[i];LL sum = 0;int pos = s.find("1");if(pos == -1){cout << 0 << endl;return ;}for(int i = pos; i < n; i ++){if(s[i] == '1'){int cnt = 1;int t = a[i];sum += t;for(int j = i + 1; j < n; j ++){if(s[j] == '0') break;else cnt ++;t = min(t, a[j]);sum += a[j];}if(i - 1 >= 0){int p = a[i - 1];if(p > t) sum += p - t;}i += cnt - 1;}}cout << sum << endl;
}int main(){IOS;int _ = 1;// cin >> _;while(_ --){solve();}return 0;}
步数
原题链接
描述:
在河工院当中有编号由 1 ∼ n 1 \sim n 1∼n 的 n n n 栋硕大的教学楼,这些教学楼之间有着非常的神奇道路,神奇到这些道路只需要一步就可以走完。
这是因为法力超强的超凡giegie制作的法力场。
河工院在设计这些教学楼之间的道路的时候为了考验学生的数学能力,每个教学楼能到达的教学楼只能是其编号的约数之和(约数之和不包含本身)并且要比其编号小的的教学楼。
即 4 4 4 号教学楼可以到达 3 3 3 号教学楼,因为 4 4 4 的约数之和为 3 3 3,并且 3 < 4 3 \lt 4 3<4。(同样 3 3 3 号也可以到 4 4 4 号教学楼,因为道路是双向的)
今日 L Y S LYS LYS 大佬闲来无事想去领略一下校园的风景,他可以从任何一栋教学楼出发,他想知道他可以走的最多步数。(因为 L Y S LYS LYS 大佬太强了不想自己算,就来考验一下你们啦)
输入格式:
输入一个数 n n n,代表有 n n n 所教学楼。
输出格式:
输出一个数,为最多步数。
数据范围:
1 ≤ n ≤ 1 0 6 1 \le n \le 10^6 1≤n≤106
样例输入:
3
样例输出:
2
提示:

思想:
-
本题比前面的题稍微复杂了那么一点点,一共有两个难点。
-
怎么建图
-
怎么求树的最长链
-
-
在这里不能直接去暴力建图,需要先预处理出来一个数组来存储每个数的约数之和。
for(int i=1;i<=n;i++)
{for(int j=2;j<=n/i;j++){sum[i*j]+=i;}
}
-
这样就可以直接来建图了。
-
第二个难点的话,就是怎么来求树的最长链,很直白的做法就是用树形DP来求,不过可以发现每条路的边权只有1,所以也可以直接用DFS或者BFS来求。
-
任意找一个点u,距离u最远距离的那个点v,再找距离v点最远的点z,v到z的距离就是最长链。
代码:
#include<bits/stdc++.h>
using namespace std;
int he[2000010],ne[2000010],e[2000010],ver[2000010];
int d[2000010],tot=0,st[2000010];
void add(int x,int y,int z)
{ver[++tot]=y;e[tot]=z;ne[tot]=he[x];he[x]=tot;
}
int ans=0,p;
int sum[1000010];
void dfs(int x,int y,int z)
{if(ans<z){ans=z;p=x;}st[x]=1;for(int i=he[x];i;i=ne[i]){if(ver[i]==y)continue;dfs(ver[i],x,z+e[i]);}
}
int main()
{int n;cin>>n;for(int i=1;i<=n;i++){for(int j=2;j<=n/i;j++){sum[i*j]+=i;}}for(int i=2;i<=n;i++){if(i>sum[i]){add(sum[i],i,1);add(i,sum[i],1);}}int anss=0;for(int i=1;i<=n;i++){if(!st[i]){ans=0;dfs(i,0,0);dfs(p,0,0);anss=max(anss,ans);}}cout<<anss;}
到达龙湖最美大学
原题链接
描述:
到达龙湖最美大学——河南工程学院,太美丽啦河南工程学院。哎哟这不 H F HF HF 嘛,再看一下远处的图书馆吧家人们…
H F HF HF 现在想要爬到图书馆楼顶,已知图书馆有 N N N 级台阶,编号为 1 ∼ N 1\sim N 1∼N,他的腿长度为 h h h,第 i i i 级台阶相较第 i − 1 i-1 i−1 级台阶的高度 d i d_i di:
- H F HF HF 最开始所处的高度为 H = 0 H = 0 H=0。
- 当且仅当 h ≥ d i h\ge d_i h≥di 时, H F HF HF 可以爬上第 i i i 级台阶。
- 若 H F HF HF 能够爬上第 i i i 级台阶,他所处的高度 H H H 就会变为 H + d i H+d_i H+di。
- H F HF HF 只能按照台阶顺序来爬,不能跨编号爬台阶。
接下来给出 N N N 个台阶的高度 d d d 以及 M M M 次询问,对于每次询问包含 M M M 个腿长 h h h,求对于每一次询问在遵循上述规则的条件下, H F HF HF 最高能到达的高度 H H H。
输入格式:
第一行,两个整数 N N N 和 M M M,分别表示台阶个数和询问次数。
第二行, N N N 个整数 d d d, d i d_i di 表示第 i i i 级台阶相较第 i − 1 i-1 i−1 级台阶的高度。
第三行, M M M 个整数 h h h, h i h_i hi 表示第 i i i 次询问的腿长。
输出格式:
共一行,每行输出在对应的询问下能到达的最大高度 H H H。
数据范围:
1 ≤ N , M ≤ 1 × 1 0 6 , 0 ≤ d , h ≤ 1 0 9 1\le N,M \le 1\times 10^6,0\le d,h\le 10^9 1≤N,M≤1×106,0≤d,h≤109。
样例输入:
6 4
1 2 1 4 4 3
1 2 3 4
样例输出:
1 4 4 15
提示:
- 对于样例:
- 当 h = 1 h = 1 h=1 时,最高可以上到 1 1 1 号台阶,最后高度 H = 1 H = 1 H=1;
- 当 h = 2 , 3 h = 2,3 h=2,3 时,最高可以上到 1 , 2 , 3 1,2,3 1,2,3 号台阶,最后高度 H = 4 H = 4 H=4;
- 当 h = 4 h = 4 h=4 时,最高可以上到 1 , 2 , 3 , 4 , 5 , 6 1,2,3,4,5,6 1,2,3,4,5,6 号台阶,最后高度 H = 15 H = 15 H=15。
思想:
- 前缀和,二分。
- 查询次数频繁,考虑前缀和存储能够上到前 i i i 级阶梯的高度。
- 预处理出上到第 i i i 个台阶所需的腿长,即对于前 i i i 级台阶,预处理出最大的高度差。
- 在询问时,对于每个腿长,二分即可快速找到最大能达到的台阶编号。
- 综上,利用前缀和处理能够上到第 i i i 个台阶时的高度,同时出预处理到达第 i i i 个台阶之前最高的台阶高度,最后二分处理每一次询问即可,时间复杂度 O ( M log N ) \mathcal{O}(M\log{N}) O(MlogN)。
代码:
#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <sstream>
#include <vector>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <unordered_map>
#include <unordered_set>using namespace std;#define IOS ios::sync_with_stdio(false),cin.tie(nullptr),cout.tie(nullptr)
#define re register
#define fi first
#define se second
#define endl '\n'typedef long long LL;
typedef pair<int, int> PII;
typedef pair<LL, LL> PLL;const int N = 1e6 + 3;
const int INF = 0x3f3f3f3f, mod = 1e9 + 7;
const double eps = 1e-6, PI = acos(-1);LL a[N], b[N];void solve(){int n, m; cin >> n >> m;LL flag = 0;for(int i = 1; i <= n; i ++){cin >> a[i];flag = max(flag, a[i]);a[i] += a[i - 1];b[i] = flag;}while(m --){int x; cin >> x;if(x == 0){cout << 0 << ' ';continue;}int pos = upper_bound(b, b + n, x) - b;if(b[pos] > x) pos --;cout << a[pos] << ' ';}cout << endl;
}int main(){IOS;int _ = 1;// cin >> _;while(_ --){solve();}return 0;}
LYS 的小小游戏
原题链接
描述:
L Y S LYS LYS 给 H F HF HF 突然提到了一个他很久很久之前发明的一个小小游戏,这个游戏需要两个人来配合,于是就和 H F HF HF 开心的玩了起来。
这个游戏就是 H F HF HF 给定一个 n n n,代表矩阵的大小是 n × n n \times n n×n 的蛇形矩阵,这个名字一定不为陌生,就是像蛇一样顺时针盘旋成一个矩阵,每一圈的数字都是顺时针排列的。就像下图一样:

不过 L Y S LYS LYS 这个小小游戏比较像这个,但又不太一样。(我称之为回字拐弯矩阵)蛇形矩阵一个人就可以玩,但是这个小小游戏需要两个人,因为需要另一个人发出指令。指令只有 1 1 1 或者 − 1 -1 −1,如果为 1 1 1,代表当前圈顺时针排列,如果是 − 1 -1 −1,就要变成逆时针排列。(具体可以看样例解释)
输入格式:
一个整数 n n n,代表矩阵的边长
第二行 ( n + 1 ) / 2 (n+1)/2 (n+1)/2 个整数,分别为 1 1 1 或 − 1 -1 −1,代表当前圈顺时针还是逆时针。
输出格式:
输出这个回字拐弯矩阵
数据范围:
1 ≤ n ≤ 1000 1 \le n \le 1000 1≤n≤1000
样例输入:
7
1 -1 -1 1
样例输出:
1 2 3 4 5 6 7
24 25 40 39 38 37 8
23 26 41 48 47 36 9
22 27 42 49 46 35 10
21 28 43 44 45 34 11
20 29 30 31 32 33 12
19 18 17 16 15 14 13
提示:

思想:
- 本题是一个模拟题,作为次签到题也是可以的。
- 直接根据题目的描述直接for循环模拟就行了,问题不大。
代码:
#include<bits/stdc++.h>
using namespace std;
int a[1100][1100],n;
int main()
{cin>>n;int ll=(n+1)/2;int cnt=0,pp=1;int oo=n;for(int i=1;i<=ll;i++){cnt++;int x;cin>>x;if(x==1){for(int j=cnt;j<=n;j++){a[cnt][j]=pp;pp++;}for(int j=cnt+1;j<=n;j++){a[j][n]=pp;pp++;}for(int j=n-1;j>=cnt;j--){a[n][j]=pp;pp++;}for(int j=n-1;j>cnt;j--){a[j][cnt]=pp;pp++;}}if(x==-1){for(int j=cnt;j<=n;j++){a[j][cnt]=pp;pp++;}for(int j=cnt+1;j<=n;j++){a[n][j]=pp;pp++;}for(int j=n-1;j>=cnt;j--){a[j][n]=pp;pp++;}for(int j=n-1;j>cnt;j--){a[cnt][j]=pp;pp++;}}n--;}for(int i=1;i<=oo;i++){for(int j=1;j<=oo;j++)cout<<a[i][j]<<' ';cout<<endl;}
}
欧拉幻树
原题链接
描述:
那一天, L Y S LYS LYS 再次回忆起了被 H F HF HF 出的真·毒瘤题——欧拉幻方支配的恐惧,这使得 L Y S LYS LYS 彻底疯狂。
奕前是奕前,仙在是仙在,奕悟之后的 L Y S LYS LYS 给出了一个长度为 n n n 的排列 p p p,要求 H F HF HF 根据 p p p 构建出他想要的欧拉幻树。
给出欧拉幻树的定义:
- 该树是一颗含有 n n n 个节点的有根树
- 对于排列 p p p,满足所有的 1 ≤ i < j ≤ n 1\le i < j \le n 1≤i<j≤n 中,使得 p i p_i pi 到根的距离小于点 p j p_j pj 到根的距离
H F HF HF 大喜,这一看就肥肠煎蛋,于是很自然地交给了你来解决。
请你对树上的边赋权,使得满足欧拉幻树的定义。若无解,输出 − 1 -1 −1 ;否则输出 n n n 个整数,第 i i i 个整数 v i v_i vi 表示点 i i i 到其父亲的边权为 v i v_i vi,特别地,根到其父亲的边权为 0 0 0 ,其他的边权至少为 1 1 1。
输入格式:
第一行输入数据包含一个整数 t t t 测试中输入数据集的数量。
每个测试用例由三行组成。
第一行包含一个整数 n n n,表示树的顶点数。
第二行包含 n n n 个整数 b 1 , b 2 , . . . , b n ( 1 ≤ b i ≤ n ) b_1,b_2,...,b_n(1\le b_i \le n) b1,b2,...,bn(1≤bi≤n) 表示 i i i 的父亲,保证是一颗有根树。
第三行包含给定的排列 p p p , n n n 个不同的整数 p i ( 1 ≤ p i ≤ n ) p_i(1\le p_i \le n) pi(1≤pi≤n)。
输出格式:
对于每组输入数据,将答案输出在单独的一行上。
如果存在解,则输出 n n n 个整数 v 1 , v 2 , . . . , v n v_1 ,v_2,...,v_n v1,v2,...,vn 表示 b i b_i bi 到 i i i 这条边的权重,特别地,对于根顶点边权为 0 0 0
如果有多个答案,请输出字典序最小的答案序列。
数据范围:
1 ≤ t ≤ 1 0 4 1\le t \le 10^4 1≤t≤104
$1 \le n \le 2\times 10^5 , \sum n \le 5\times 10^5 $
样例输入:
4
5
3 1 3 3 1
3 1 2 5 4
3
1 1 2
3 1 2
7
1 1 2 3 4 5 6
1 2 3 4 5 6 7
6
4 4 4 4 1 1
4 2 1 5 6 3
样例输出:
1 1 0 4 2
-1
0 1 1 1 1 1 1
2 1 5 0 1 2
思想:
- 首先,判断是否存在解:
- 如果一个点的某个儿子到根的距离比自己短那么一定是不合法的,其他情况都是合法的
- 遍历每个节点,对于每个节点 x x x,检查其所有子节点 y y y,如果存在一个子节点 y y y,使得 y y y 到根的距离比 x x x 到根的距离更短,那么该排列没有解,输出 − 1 -1 −1
- 如果存在解:
- 则按照字典序最小的方式给每个节点赋值。
- 将排列 p p p 中的节点按照从小到大的顺序遍历,对于排列中的第 i i i 个节点 p i p_i pi,将其赋值为 i i i
- 赋值完成后,再 DFS 一遍给每条边赋值:
- 从根节点开始,对于每个节点 x x x,遍历其所有子节点 y y y,将边 ( x , y ) (x, y) (x,y) 的权值设为 p y − p x p_y - p_x py−px 即可
代码:
#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <sstream>
#include <vector>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <unordered_map>
#include <unordered_set>using namespace std;#define IOS ios::sync_with_stdio(false),cin.tie(nullptr),cout.tie(nullptr)
#define re register
#define fi first
#define se second
#define endl '\n'typedef long long LL;
typedef unsigned long long ULL;
typedef pair<int, int> PII;
typedef pair<LL, LL> PLL;const int N = 1e6 + 3;
const int INF = 0x3f3f3f3f, mod = 1e9 + 7;
const double eps = 1e-6, PI = acos(-1);vector<vector<int>> tree; // 存储树的邻接表
vector<int> ans; // 存储每个节点到其父节点的边权
vector<int> vis; // 存储每个节点在排列中的位置
vector<int> res; // 存储排列
int n, flag = 1; // n为节点个数,flag用于判断是否满足欧拉幻树的定义// 检查是否满足欧拉幻树的定义
void check(int x, int fa) {for (auto y : tree[x]) {if (y == fa) continue;if (res[y] < res[x]) flag = 0; // 如果存在满足条件的边,则不满足欧拉幻树的定义check(y, x);}
}// 深度优先搜索构建欧拉幻树
void dfs(int x, int fa, int deep) {ans[x] = vis[x] - deep; // 节点x到其父节点的边权为节点在排列中的位置减去当前深度for (auto y : tree[x]) {if (y == fa) continue;dfs(y, x, deep + ans[x]);}
}void solve() {cin >> n;tree = vector<vector<int>>(n);int root = -1;for (int i = 0; i < n; i ++) {int x; cin >> x;x --;if (x == i) {root = x; // 找到根节点continue;}tree[x].push_back(i);tree[i].push_back(x);}res = vector<int>(n);vector<int> st(n);for (int i = 0; i < n; i ++) {cin >> st[i]; st[i]--; res[st[i]] = i; // 将排列中的位置记录在res数组中}flag = 1;check(root, -1); // 检查是否满足欧拉幻树的定义ans = vector<int>(n);if (!flag) {cout << -1 << "\n"; // 如果不满足欧拉幻树的定义,则输出-1return;}vis = vector<int>(n);int cnt = 0;for (int i = 0; i < n; i ++) vis[st[i]] = cnt ++; // 将排列中的位置映射到节点编号dfs(root, -1, 0);for (int i = 0; i < n; i ++) cout << ans[i] << " \n"[i == n - 1]; // 输出每个节点到其父节点的边权
}int main(){IOS;int _ = 1;cin >> _;while(_ --){solve();}return 0;}
相关文章:

河南工程学院第六届程序设计竞赛-A组-题解
更好的阅读体验 \color{red}{更好的阅读体验} 更好的阅读体验 远古时期的签到题 原题链接 描述: 远古时期奇妙的事情… 远古时期有一个比赛,里面有这样一道签到题: 给定一个正整数 N N N求这个整数转化为二进制后的数有多少位是 0 0 0。…...
客户端启动与交互流程)
韩版传奇 2 源码分析与 Unity 重制(二)客户端启动与交互流程
专题介绍 该专题将会分析 LOMCN 基于韩版传奇 2,使用 .NET 重写的传奇源码(服务端 客户端),分析数据交互、状态管理和客户端渲染等技术,此外笔者还会分享将客户端部分移植到 Unity 和服务端用现代编程语言重写的全过…...

JVM面试——运行时数据区
一:JVM的运行时内存区域是怎样的? 根据Java虚拟机规范的定义,JVM的运行时内存区域主要由程序计数器、虚拟机栈、本地方法 栈、Java堆、方法区和以及运行时常量池组成。其中堆、方法区以及运行时常量池是线程之间共享的区域,而栈(…...
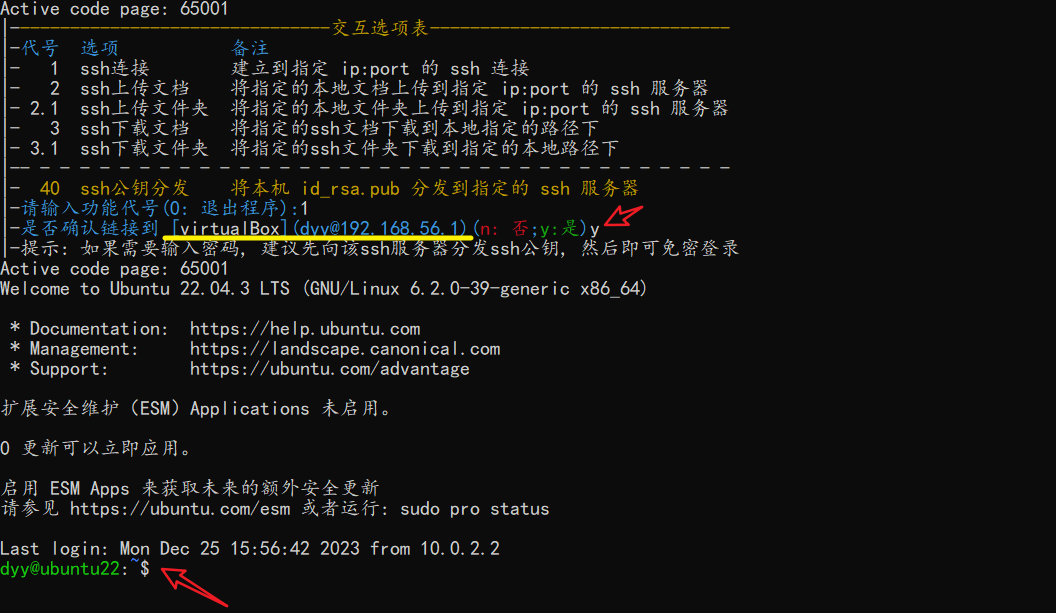
ssh工具 向指定的ssh服务器配置公钥
此文分享一个python脚本,用于向指定的ssh服务器配置公钥,以达到免密登录ssh服务器的目的。 效果演示 🔥完整演示效果 👇第一步,显然,我们需要选择功能 👇第二步,确认 or 选择ssh服务器 👇第三步,输入ssh登录密码,以完成公钥配置 👇验证,我们通过ssh登录…...
uni-app pages.json之globalStyle全局页面样式配置
锋哥原创的uni-app视频教程: 2023版uniapp从入门到上天视频教程(Java后端无废话版),火爆更新中..._哔哩哔哩_bilibili2023版uniapp从入门到上天视频教程(Java后端无废话版),火爆更新中...共计23条视频,包括:第1讲 uni…...
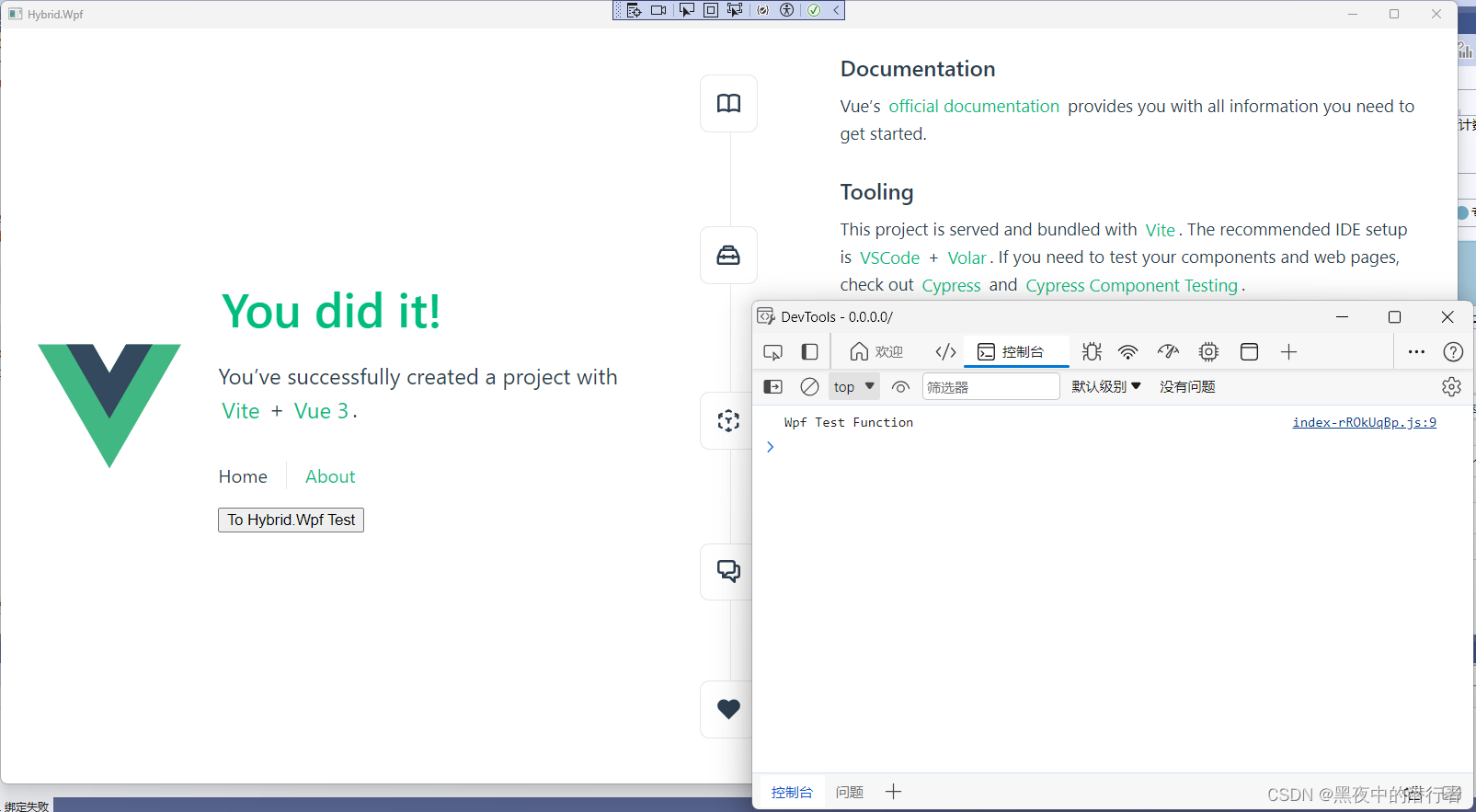
Blazor 混合开发_MAUI+Vue_WPF+Vue
Blazor 混合开发_MAUIVue_WPFVue 背景混合开发的核心为什么必须使用 wwwroot 文件夹放置 Web 项目文件 创建 MAUI 项目创建 wwwroot 文件夹服务注册创建 _import.razor添加 Main.razor 组件修改 MainPage.xaml 文件 创建 WPF 项目创建 wwwroot 文件夹服务注册创建 _import.razo…...

udp异步方式接收消息
C#实现 //定义结构体 public struct UdpState { public UdpClient u; public IPEndPoint e; } private UdpClient _client; //_client的初始化请参考其他资料 IPEndPoint remoteEP null; //TODO //public static bool mess…...
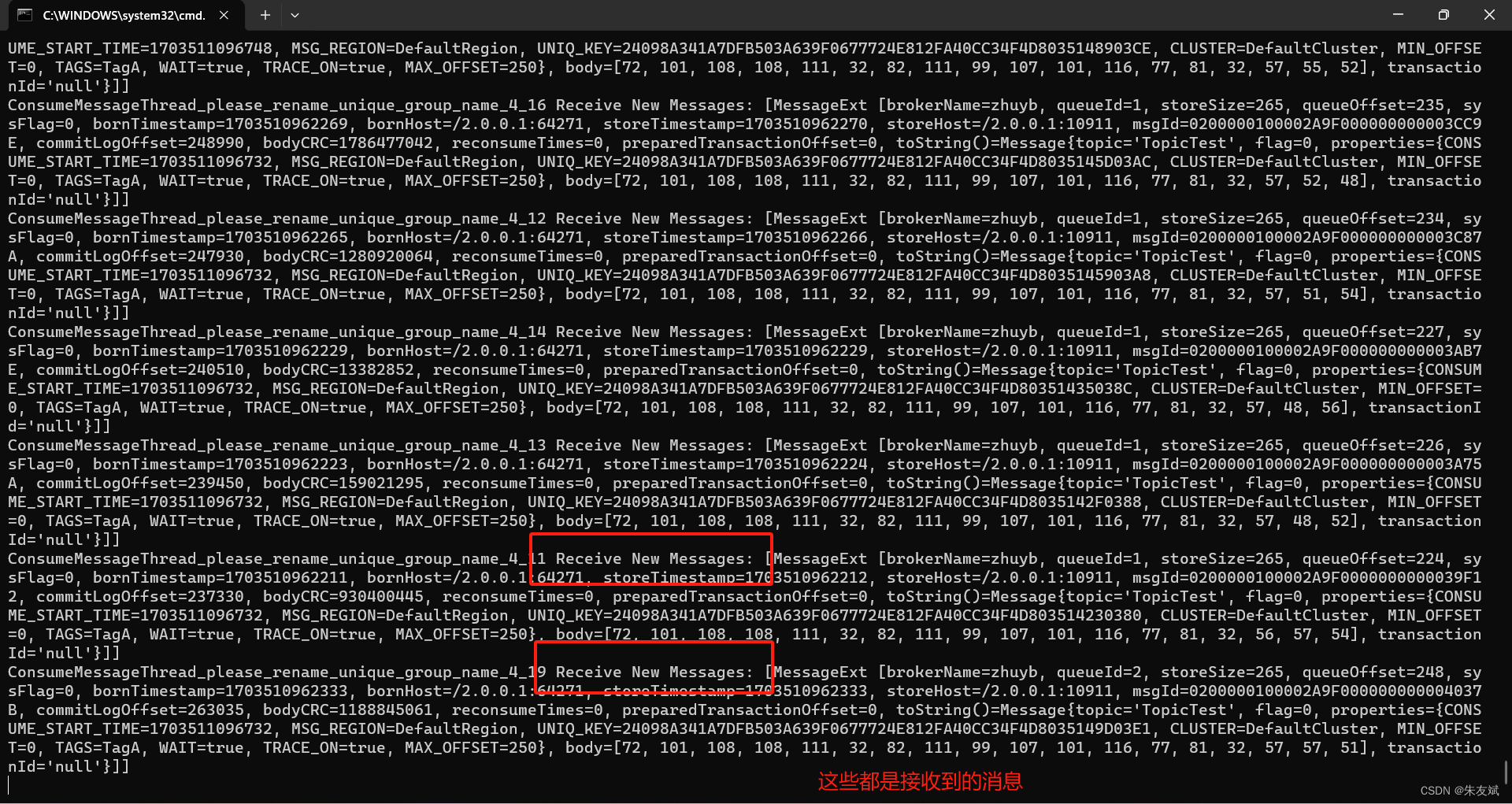
【RocketMQ笔记01】安装RocketMQ消息队列运行环境
这篇文章,主要介绍如何安装RocketMQ消息队列运行环境。 目录 一、RocketMQ消息队列 1.1、下载RocketMQ 1.2、解压安装包 1.3、配置RocketMQ环境变量 1.4、修改启动脚本 1.5、启动RocketMQ (1)启动NameServer (2࿰…...

使用 Privoxy 实现对多域名的定向转发
需求与思路 内网一台主机想要访问公网的两个不同站点, 想要实现访问两个站点时表现出不同的公网 IP 地址. 即在公网的站点服务器端看到的客户端 IP 是不同的. 思路是搭建两台具有不同公网 IP 的服务器, 分别安装配置 Privoxy 后进行串联, 并将其中一台作为主服务器暴露给内网…...

《PySpark大数据分析实战》-19.NumPy介绍ndarray介绍
📋 博主简介 💖 作者简介:大家好,我是wux_labs。😜 热衷于各种主流技术,热爱数据科学、机器学习、云计算、人工智能。 通过了TiDB数据库专员(PCTA)、TiDB数据库专家(PCTP…...
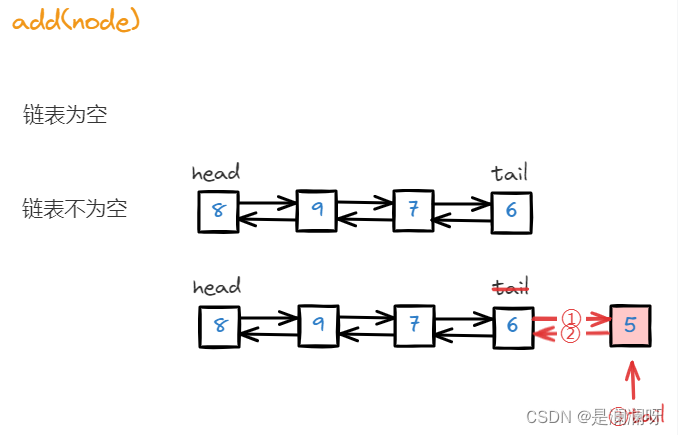
图解LRU缓存
图解LRU缓存 OJ链接 介绍 LRU 缓存机制可以通过哈希表辅以双向链表实现,我们用一个哈希表和一个双向链表维护所有在缓存中的键值对。 双向链表按照被使用的顺序存储了这些键值对,靠近尾部的键值对是最近使用的,而靠近头部的键值对是最久未…...

FFmpeg常见命令行
1、ffmpeg命令行 视频生成图片 ffmpeg -i test.mp4 -r 25 -f image2 data/image%3d.jpg这个命令行使用FFmpeg工具将视频文件(test.mp4)转换为一系列图像文件。 让我们逐个解释每个参数的含义: -i test.mp4: 指定输入文件为test.mp4。-i是F…...
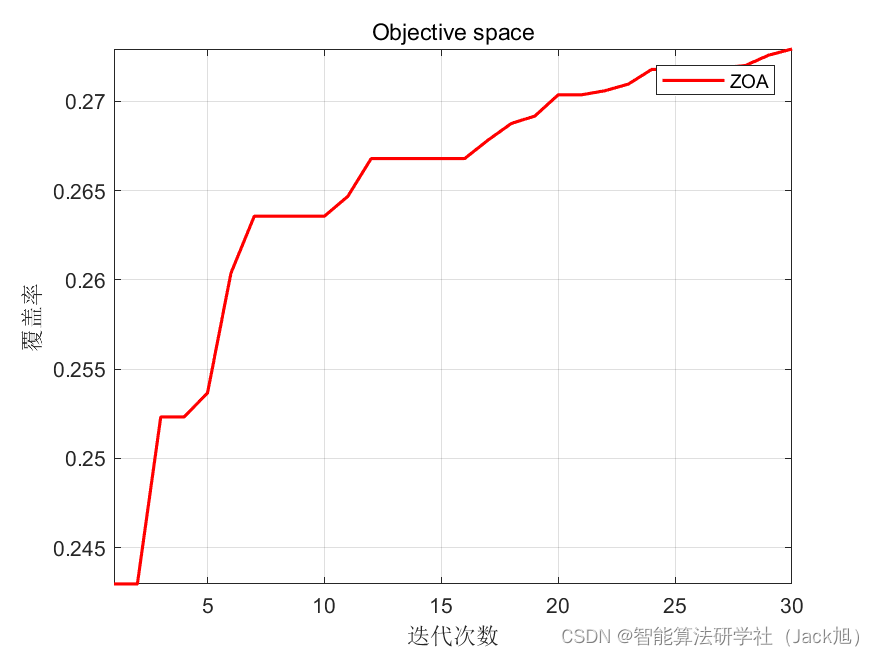
智能优化算法应用:基于斑马算法3D无线传感器网络(WSN)覆盖优化 - 附代码
智能优化算法应用:基于斑马算法3D无线传感器网络(WSN)覆盖优化 - 附代码 文章目录 智能优化算法应用:基于斑马算法3D无线传感器网络(WSN)覆盖优化 - 附代码1.无线传感网络节点模型2.覆盖数学模型及分析3.斑马算法4.实验参数设定5.算法结果6.参考文献7.MA…...

《C++避坑神器·二十五》简单搞懂json文件的读写之遍历json文件读写
json.hpp库放在文章末尾 1、遍历json文件读写 (1)插入新键值对到json之情形1 原来json文件如下所示: {"Connection": {"IpAddress": "192.168.20.1","Rock": 0,"Solt": 1}, "Data…...
使用 fixture 机制重构 appium_helloworld
一、前置说明 在 pytest 基础讲解 章节,介绍了 pytest 的特性和基本用法,现在我们可以使用 pytest 的一些机制,来重构 appium_helloworld 。 appium_helloworld 链接: 编写第一个APP自动化脚本 appium_helloworld ,将脚本跑起来 代码目录结构: pytest.ini 设置: [pyt…...
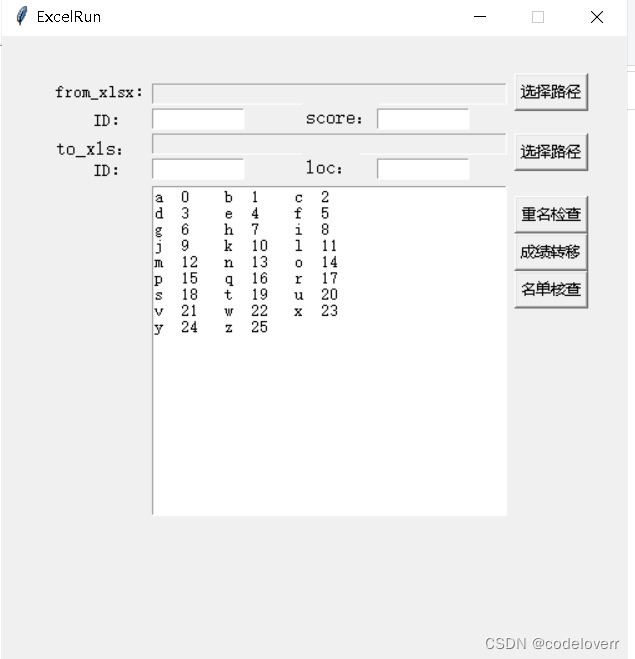
基于python的excel检查和读写软件
软件版本:python3.6 窗口和界面gui代码: class mygui:def _init_(self):passdef run(self):root Tkinter.Tk()root.title(ExcelRun)max_w, max_h root.maxsize()root.geometry(f500x500{int((max_w - 500) / 2)}{int((max_h - 300) / 2)}) # 居中显示…...

Podman配置mongodb
文章目录 查询镜像拉取镜像查看镜像运行容器创建root用户 查询镜像 podman search mongo拉取镜像 podman pull docker.io/library/mongo查看镜像 podman images运行容器 podman run -d -p 27017:27017 --namemongodb-test docker.io/library/mongo创建root用户 podman exe…...
java实现矩阵谱峰搜索算法
矩阵谱峰搜索算法,也称为矩阵谱峰查找算法,是一种用于搜索二维矩阵中谱峰的方法。谱峰是指在矩阵中的一个元素,它比其上下左右四个相邻元素都大或相等。 该算法的基本思想是从矩阵的中间列开始,找到该列中的最大元素,…...
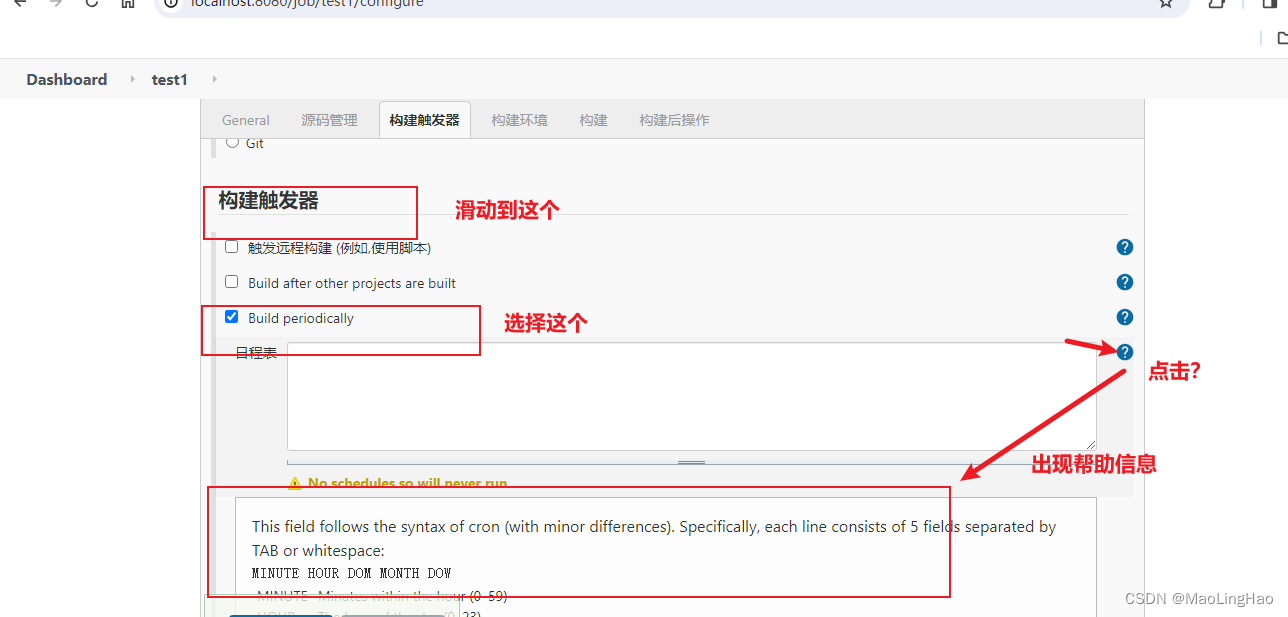
Jenkins的特殊操作定时自动执行任务以及测试报告调优
java -Dhudson.model.DirectoryBrowserSupport.CSP -jar Jenkins.war 测试报告 不美丽 执行上面的代码 重启jenkins 就好了...
【Grafana】Grafana匿名访问以及与LDAP连接
上一篇文章利用Docker快速部署了Grafana用来展示Zabbix得监控数据,但还需要给用户去创建账号允许他们登录后才能看展示得数据,那有什么办法让非管理员更方便得去访问Grafana呢?下面介绍两个比较方便实现的: 在开始设置前ÿ…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...
