力扣题目学习笔记(OC + Swift)21. 合并两个有序链表
21. 合并两个有序链表
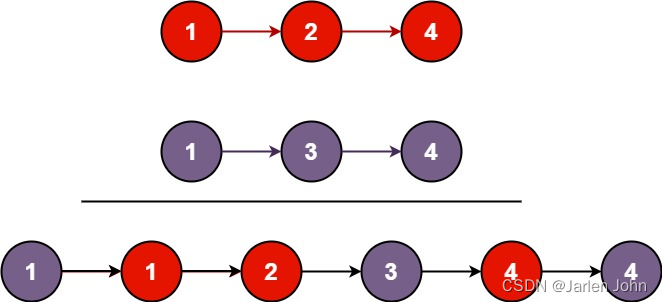
将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。
链表解题经典三把斧:
- 哑巴节点
- 栈
- 快慢指针
此题比较容易想到的解法是迭代法,生成哑巴节点,然后迭代生成后续节点。
方法一、迭代法
Swift
func mergeTwoLists(_ list1: ListNode?, _ list2: ListNode?) -> ListNode? {guard list1 != nil else {return list2}guard list2 != nil else {return list1}var list1 = list1var list2 = list2let dummyNode = ListNode(-1);var prev:ListNode? = dummyNodewhile list1 != nil && list2 != nil {if list1!.val < list2!.val {prev?.next = list1list1 = list1!.next}else {prev?.next = list2list2 = list2!.next}prev = prev?.next}prev?.next = (list1 != nil) ? list1 : list2return dummyNode.next}
OC
//回溯法
- (ListNodeOC *_Nullable)mergeTwoLists:(ListNodeOC * _Nullable)list1list2:(ListNodeOC * _Nullable)list2 {if (!list1) {return list2;}if (!list2) {return list1;}ListNodeOC *dummyNode = [[ListNodeOC alloc] initWithVal:-1];ListNodeOC *pre = dummyNode;while (list1 && list2) {if (list1.val < list2.val) {pre.next = list1;list1 = list1.next;}else {pre.next = list2;list2 = list2.next;}pre = pre.next;}pre.next = list1 ? list1 : list2;return dummyNode.next;
}方法二、递归法
代码简洁、思路清晰、稍占内存的解法。
Swift
func mergeTwoLists(_ list1: ListNode?, _ list2: ListNode?) -> ListNode? {guard let list1 = list1 else { return list2 }guard let list2 = list2 else { return list1 }if list1.val < list2.val {list1.next = mergeTwoLists(list1.next, list2)return list1}else {list2.next = mergeTwoLists(list1, list2.next)return list2}}
OC
//递归法
- (ListNodeOC * _Nullable)mergeTwoLists:(ListNodeOC * _Nullable)list1list2:(ListNodeOC * _Nullable)list2 {//递归终止条件if (!list1) {return list2;}if (!list2) {return list1;}if (list1.val < list2.val) {list1.next = [self mergeTwoLists:list1.next list2:list2];return list1;}else {list2.next = [self mergeTwoLists:list1 list2:list2.next];return list2;}
}相关文章:
力扣题目学习笔记(OC + Swift)21. 合并两个有序链表
21. 合并两个有序链表 将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。 链表解题经典三把斧: 哑巴节点栈快慢指针 此题比较容易想到的解法是迭代法,生成哑巴节点,然后迭代生成后续节点。…...
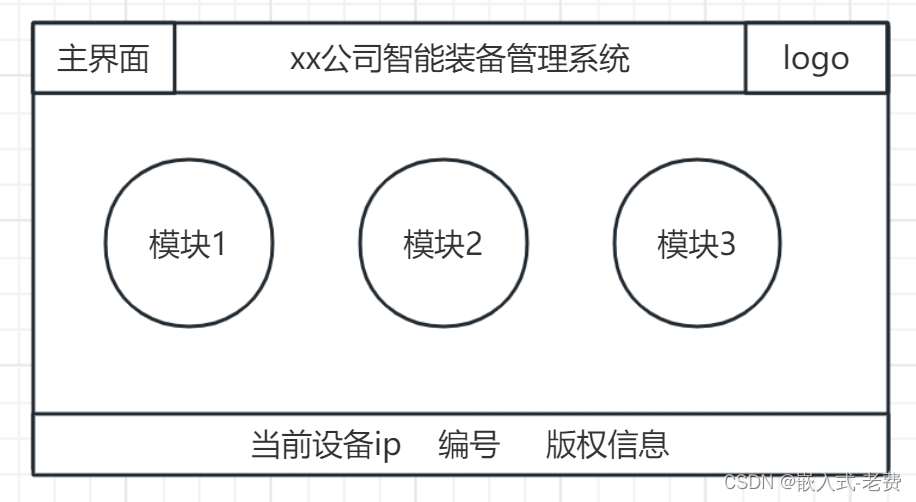
C# WPF上位机开发(windows pad上的应用)
【 声明:版权所有,欢迎转载,请勿用于商业用途。 联系信箱:feixiaoxing 163.com】 大部分同学可能都认为c# wpf只能用在pc端。其实这是一种误解。c# wpf固然暂时只能运行在windows平台上面,但是windows平台不仅仅是电脑…...

Word使用技巧【开题报告】
1、修改目录:选中目录,点击更新域。 2、更改或删除单个页面上的页眉或页脚 3、借助其他软件在Word导入参考文献 利用zetero导入文献:安装zetero 解决参考文献插入问题 在Word中插入文献操作步骤 英文文献出现“等”,如何解决 Zote…...

电子学会C/C++编程等级考试2022年06月(七级)真题解析
C/C++等级考试(1~8级)全部真题・点这里 第1题:有多少种二叉树 输入n(1<n<13),求n个结点的二叉树有多少种形态 时间限制:1000 内存限制:65536输入 整数n输出 答案 样例输入 3样例输出 5 答案: //参考答案 #include<bits/stdc++.h> using namespace std; …...
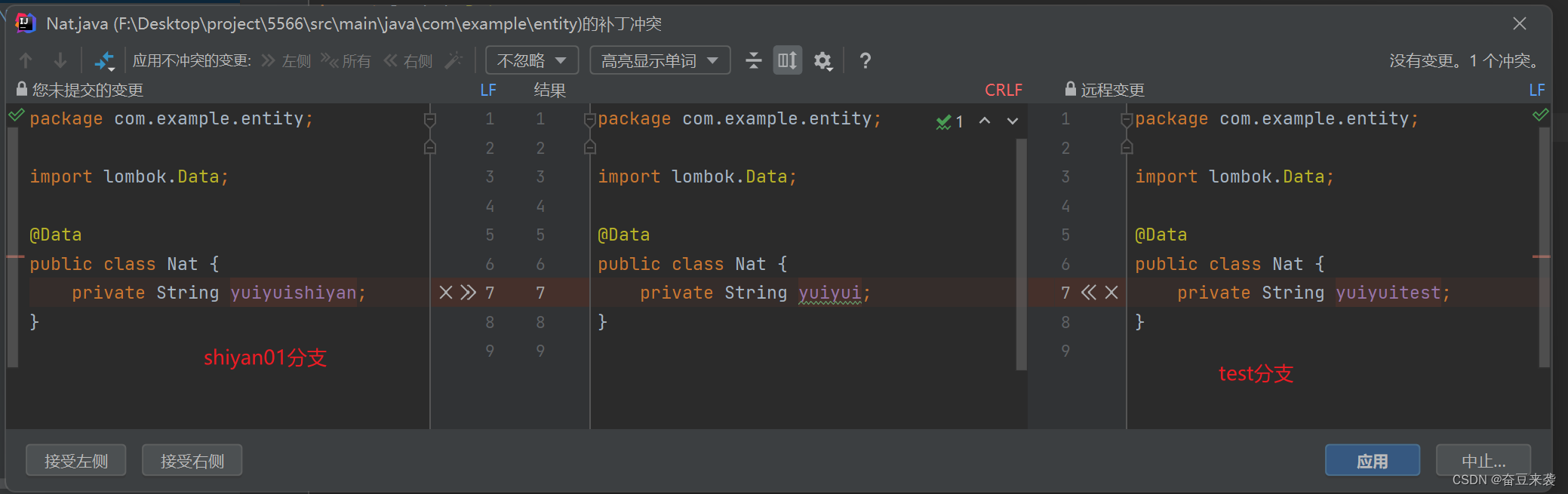
git中的smart checkout和force checkout
切换分支时出现了这个问题: 这是因为shiyan01分支修改了代码,但是没有commit, 所以在切换到test分支的时候弹出这个窗口 一、smart checkout(智能签出) 会把shiyan01分支的改动内容带到test分支。合并处理后的内容就变成了test分支的内容,而shiyan01分支的改动会被…...

vue3整合Element-Plus,极速上手。
条件分页查询: 需求分析: form表单 Button按钮 Table表格 Pagination分页 页面布局: 搜索表单: 如果表单封装的数据较多,建议绑定到一个对象中。 …...

学习Vue2.x
文章目录 一、使用Vue脚手架1.ref和props属性2.mixin混入3.组件化编码流程4.webStorage5.组件自定义事件6.全局事件总线7.消息订阅与发布 二、使用步骤1.引入库 一、使用Vue脚手架 1.ref和props属性 ref属性: (1)被用来给元素或子组件注册应…...
)
新手如何快速熟悉代码,写出东西(持续更新)
目录 第一章、最小编程任务的设想1.1)程序员入门会遇到的问题1.2)最小编程任务的设想1.3)编程逻辑1.4)具体需求 第二章、最小编程单元的练习2.1)代码/需求方面2.1.1)初级练习2.1.2)中级练习2.1.…...
)
11-网络安全框架及模型-软件安全能力成熟度模型(SSCMM)
目录 软件安全能力成熟度模型 1 背景概述 2 主要内容 3 成熟度等级定义 4 关键过程和实践 5 评估方法 6 改进建议 7 持续改进 8 主要价值 9 应用场景 10 优势和局限性 备注 软件安全能力成熟度模型 1 背景概述 SSCMM模型是软件安全能力成熟度模型,它描…...

Linux操作系统基础知识点
Linux是一种计算机操作系统,其内核由林纳斯本纳第克特托瓦兹(Linus Benedict Torvalds)于1991年首次发布。Linux操作系统通常与GNU套件一起使用,因此也被称为GNU/Linux。它是一种类UNIX的操作系统,设计为多用户、多任务…...
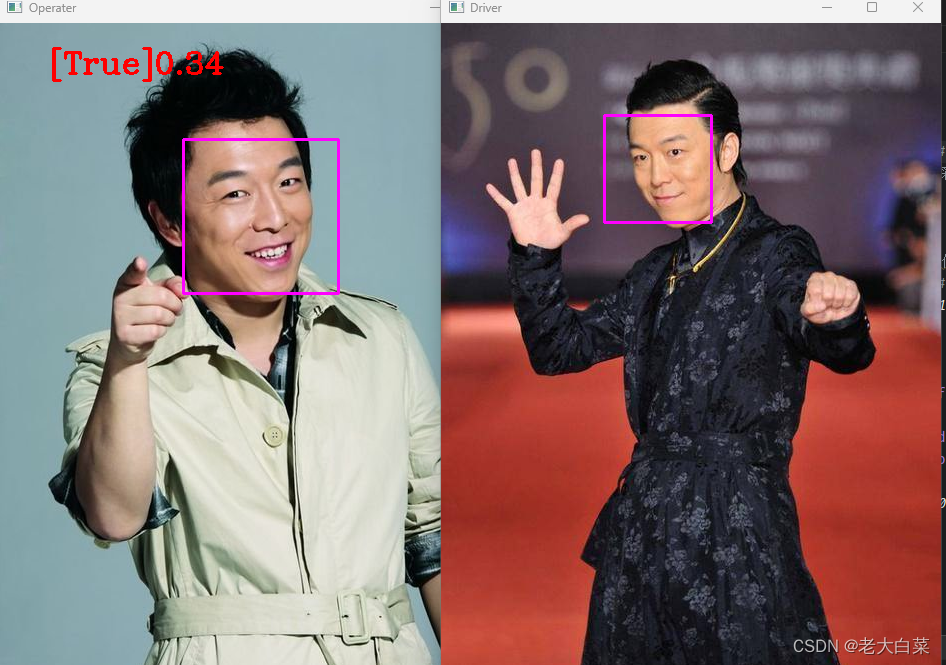
python 通过opencv及face_recognition识别人脸
效果: 使用Python的cv2库和face_recognition库来进行人脸检测和比对的 0是代表一样 认为是同一人。 代码: pip install opencv-python pip install face_recognition# 导入cv2库,用于图像处理 import cv2 # 导入face_recognition库&#…...

Android开发中常见的Hook技术有哪些?
Hook技术介绍 Hook技术是一种在软件开发中常见的技术,它允许开发者在特定的事件发生时插入自定义的代码逻辑。常见的应用场景包括在函数调用前后执行特定的操作,或者在特定的事件发生时触发自定义的处理逻辑。 在Android开发中,Hook通常是通…...

【linux c多线程】线程的创建,线程信息的获取,获取线程返回值
线程创建 专栏内容: 参天引擎内核架构 本专栏一起来聊聊参天引擎内核架构,以及如何实现多机的数据库节点的多读多写,与传统主备,MPP的区别,技术难点的分析,数据元数据同步,多主节点的情况下对…...

MFC或QT中,自绘控件的目的和实现步骤
MFC自绘控件的步骤 自绘控件的目的是为了能够自定义控件的外观、行为和交互方式,以满足特定的需求,同时增强应用程序的用户体验。 实现步骤如下: 1、创建一个继承自MFC控件基类(如CButton、CStatic等)的自定义控件类…...
)
ceph集群搭建详细教程(ceph-deploy)
ceph-deploy比较适合生产环境,不是用cephadm搭建。相对麻烦一些,但是并不难,细节把握好就行,只是命令多一些而已。 实验环境 服务器主机public网段IP(对外服务)cluster网段IP(集群通信&#x…...
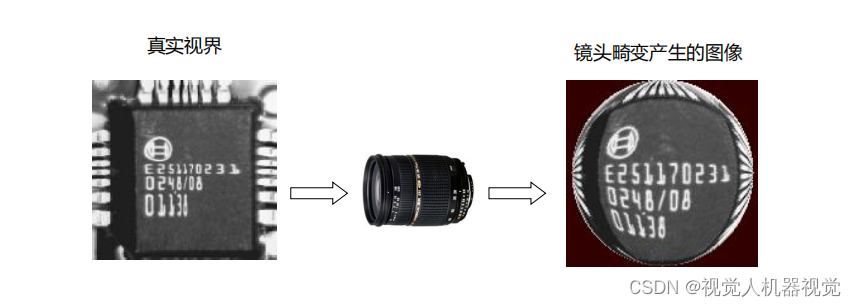
机器视觉系统选型-避免畸变
在定位及高精度测量的系统中,镜头畸变的影响尤其重要 • 使用远心镜头 • 进行系统标定...
的原理和应用)
机器学习笔记 - 线性判别分析(LDA)的原理和应用
一、LDA简述 线性判别分析(LDA)是监督机器学习中用于解决多类分类问题的一种方法。LDA通过数据降维来分离具有多个特征的多个类。这项技术在数据科学中很重要,因为它有助于优化机器学习模型。 线性判别分析,也称为正态判别分析 (NDA) 或判别函数分析 (DFA),遵循生成模型框…...
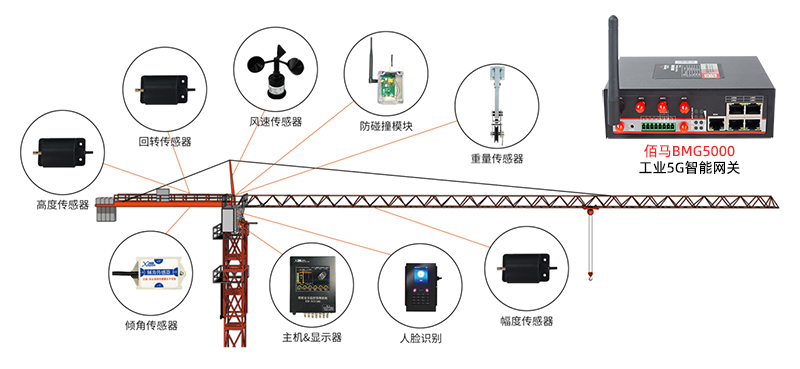
基于5G智能网关的智慧塔吊监测方案
塔吊是建筑施工中必不可少的设施,由于塔吊工作重心高、起重载荷大、人工视距/视角受限等因素,也使得塔吊在工作过程中着较多的危险因素。对此,可以部署基于工业5G智能网关搭建智慧塔吊安全监测系统,实现对塔吊运行的全局精细监测感…...

CountDownLatch详解以及用法示例
一、什么是CountDownLatch CountDownLatch中count down是倒数的意思,latch则是门闩的含义。整体含义可以理解为倒数的门栓。 CountDownLatch的作用也是如此,在构造CountDownLatch(int count):的时候需要传入一个整数count,在这个…...

【http】缓存协议
✨ 专栏介绍 在当今互联网时代,计算机网络已经成为了人们生活和工作中不可或缺的一部分。而要实现计算机之间的通信和数据传输,就需要依靠各种网络协议来进行规范和约束。无论是浏览网页、发送电子邮件还是进行在线交流,都离不开各种各样的网…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...
