纯CSS的华为充电动画,它来了
📢 鸿蒙专栏:想学鸿蒙的,冲
📢 C语言专栏:想学C语言的,冲
📢 VUE专栏:想学VUE的,冲这里
📢 Krpano专栏:想学Krpano的,冲
🔔 上述专栏,都在不定期持续更新中!!!!!!!!!!!!!
文章目录
✨ 关键点
✨ 效果演示
✨ 分析逻辑
✨ 下面附上完整代码
✨ 关键点
拆解一下知识点,最主要的其实是用到了 filter: contrast() 以及 filter: blur() 这两个滤镜,可以很好的实现这种融合效果。
单独将两个滤镜拿出来,它们的作用分别是:
filter: blur(): 给图像设置高斯模糊效果。filter: contrast(): 调整图像的对比度。
但是,当他们“合体”的时候,产生了奇妙的融合现象。
先来看一个简单的例子:

仔细看两圆相交的过程,在边与边接触的时候,会产生一种边界融合的效果,通过对比度滤镜把高斯模糊的模糊边缘给干掉,利用高斯模糊实现融合效果。
✨ 效果演示

✨ 分析逻辑
1、首先我们注意分析,这个效果到底需要怎样的结构去实现
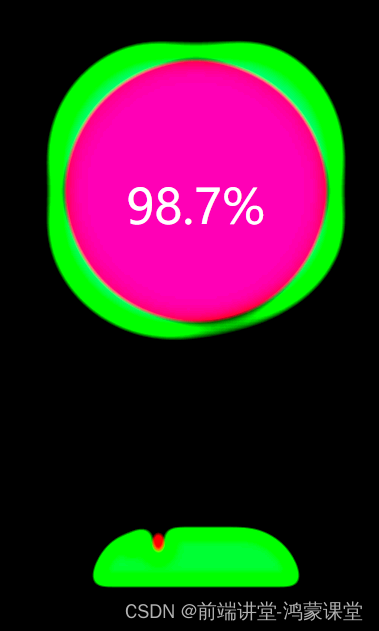
为了更好的看效果 我把所有的元素做了颜色区分,顶部其实就是两个圆利用border-radius去设置了圆角边框的弧度,下面呢?
底部也是一个大圆,其中有很多很多个小圆,因为小圆要向上移动,实现效果,主要的代码如下:
@for $i from 0 through 15 { li:nth-child(#{$i}) {$width: 15 + random(15) + px;left: 15 + random(70) + px;top: 50%;transform: translate(-50%, -50%);width: $width;height: $width;animation: moveToTop #{random(6) + 3}s ease-in-out -#{random(5000)/1000}s infinite;}
}
@keyframes moveToTop {90% {opacity: 1;}100% {opacity: .1;transform: translate(-50%, -180px);}
}注意:
- CSS本身不支持@for循环,这是一种Sass/SCSS的语法
✨ 下面附上完整代码
HTML:
<div class="g-container"><div class="g-number">98.7%</div><div class="g-contrast"><div class="g-circle"></div><ul class="g-bubbles"><li></li><li></li><li></li><li></li><li></li><li></li><li></li><li></li><li></li><li></li><li></li><li></li><li></li><li></li><li></li></ul></div>
</div>SCSS
html,
body {width: 100%;height: 100%;display: flex;background: #000;overflow: hidden;
}
.g-number {position: absolute;width: 300px;top: 27%;text-align: center;font-size: 32px;z-index: 10;color: #fff;
}.g-container {position: relative;width: 300px;height: 400px;margin: auto;
}.g-contrast {filter: contrast(10) hue-rotate(0);width: 300px;height: 400px;background-color: #000;overflow: hidden;animation: hueRotate 10s infinite linear;
}.g-circle {position: relative;width: 300px;height: 300px;box-sizing: border-box;filter: blur(8px);&::after {content: "";position: absolute;top: 40%;left: 50%;transform: translate(-50%, -50%) rotate(0);width: 200px;height: 200px;background-color: #00ff6f;border-radius: 42% 38% 62% 49% / 45%;animation: rotate 10s infinite linear;}&::before {content: "";position: absolute;width: 176px;height: 176px;top: 40%;left: 50%;transform: translate(-50%, -50%);border-radius: 50%;background-color: #000;z-index: 10;}
}.g-bubbles {position: absolute;left: 50%;bottom: 0;width: 100px;height: 40px;transform: translate(-50%, 0);border-radius: 100px 100px 0 0;background-color: #00ff6f;filter: blur(5px);
}li {position: absolute;border-radius: 50%;background: #00ff6f;
}@for $i from 0 through 15 { li:nth-child(#{$i}) {$width: 15 + random(15) + px;left: 15 + random(70) + px;top: 50%;transform: translate(-50%, -50%);width: $width;height: $width;animation: moveToTop #{random(6) + 3}s ease-in-out -#{random(5000)/1000}s infinite;}
}@keyframes rotate {50% {border-radius: 45% / 42% 38% 58% 49%;}100% {transform: translate(-50%, -50%) rotate(720deg);}
}@keyframes moveToTop {90% {opacity: 1;}100% {opacity: .1;transform: translate(-50%, -180px);}
}@keyframes hueRotate {100% {filter: contrast(15) hue-rotate(360deg);}
}注意注意注意:一定要用SCSS!!!!!!!!!!!!
注意注意注意:一定要用SCSS!!!!!!!!!!!!
注意注意注意:一定要用SCSS!!!!!!!!!!!!
我们改日再会
相关文章:

纯CSS的华为充电动画,它来了
📢 鸿蒙专栏:想学鸿蒙的,冲 📢 C语言专栏:想学C语言的,冲 📢 VUE专栏:想学VUE的,冲这里 📢 Krpano专栏:想学Krpano的,冲 🔔…...

在架构设计中,前后端分离有什么好处?
前后端分离是一种架构设计模式,将前端和后端的开发分别独立进行,它带来了多方面的好处: 1、独立开发和维护: 前后端分离允许前端和后端开发团队独立进行工作。这意味着两个团队可以并行开发,提高了整体的开发效率。前…...

C语言中的结构体和联合体:异同及应用
文章目录 C语言中的结构体和联合体:异同及应用1. 结构体(Struct)的概述代码示例: 2. 联合体(Union)的概述代码示例: 3. 结构体与联合体的异同点相同点:不同点:代码说明 结…...

文件夹共享(普通共享和高级共享的区别)防火墙设置(包括了jdk安装和Tomcat)
文章目录 一、共享文件1.1为什么需要配置文件夹共享功能?1.2配置文件共享功能1.3高级共享和普通共享的区别: 二、防火墙设置2.1先要在虚拟机上安装JDK和Tomcat供外部访问。2.2设置防火墙: 一、共享文件 1.1为什么需要配置文件夹共享功能&…...

❀My排序算法学习之冒泡排序❀
目录 冒泡排序(Bubble Sort):) 一、定义 二、算法原理 三、算法分析 时间复杂度 算法稳定性 算法描述 C语言 C++ 算法比较 插入排序 选择排序 快速排序 归并排序 冒泡排序(Bubble Sort):) 一、定义 冒泡排序(Bubble Sort),是一种计算机科学领域的较简单…...

服务器数据恢复-raid6离线磁盘强制上线后分区打不开的数据恢复案例
服务器数据恢复环境: 服务器上有一组由12块硬盘组建的raid6磁盘阵列,raid6阵列上层有一个lun,映射到WINDOWS系统上使用,WINDOWS系统划分了一个GPT分区。 服务器故障&分析: 服务器在运行过程中突然无法访问。对服务…...

Zookeeper在分布式命名服务中的实践
Java学习面试指南:https://javaxiaobear.cn 命名服务是为系统中的资源提供标识能力。ZooKeeper的命名服务主要是利用ZooKeeper节点的树形分层结构和子节点的顺序维护能力,来为分布式系统中的资源命名。 哪些应用场景需要用到分布式命名服务呢࿱…...
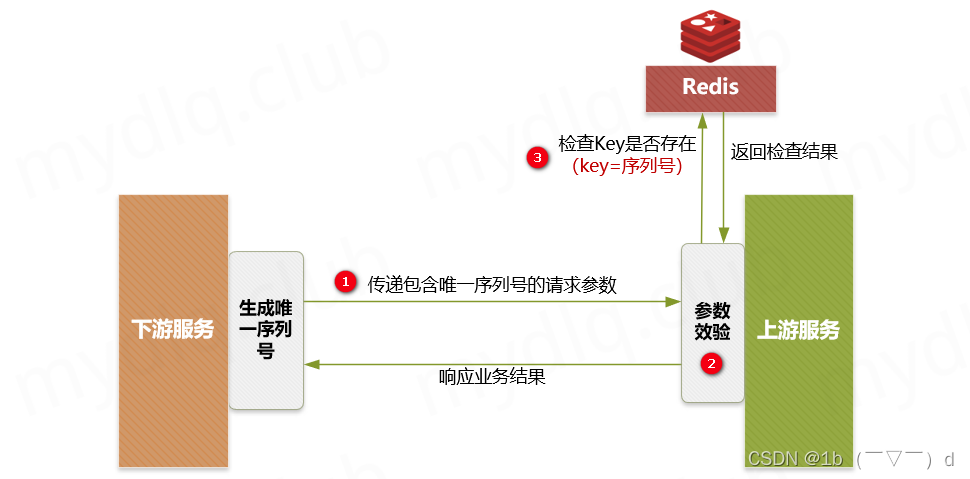
说说 Spring Boot 实现接口幂等性有哪几种方案?
一、什么是幂等性 幂等是一个数学与计算机学概念,在数学中某一元运算为幂等时,其作用在任一元素两次后会和其作用一次的结果相同。 在计算机中编程中,一个幂等操作的特点是其任意多次执行所产生的影响均与一次执行的影响相同。幂等函数或幂等…...
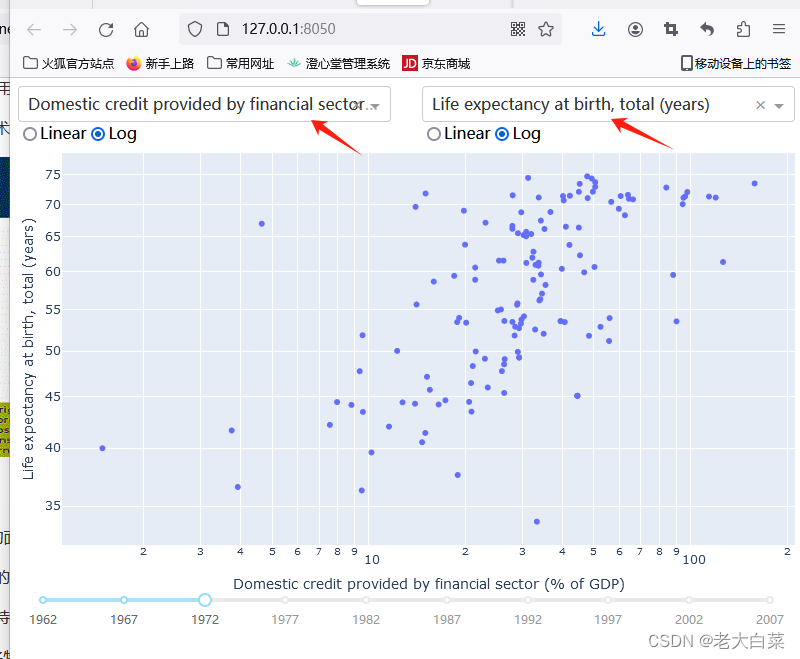
Dash中的callback的使用 多input 6
代码说明 import plotly.express as pxmport plotly.express as px用于导入plotly.express模块并给它起一个别名px。这样在后续的代码中,你可以使用px来代替plotly.express,使代码更加简洁。 plotly.express是Plotly的一个子模块,用于快速创…...
)
平方矩阵()
平方矩阵1 平方矩阵2 曼哈顿距离 #include<iostream> #include<algorithm> #include<cstdio> #include<cstring>using namespace std;const int N 110;int n; int a[N][N];int main() {while(cin >> n, n){for (int i 0; i < n; i )fo…...
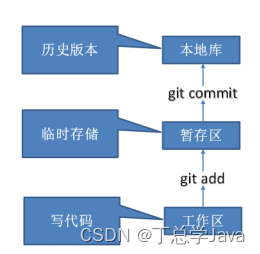
git基本命令
1、安装 介绍 安装 配置 2、git基本命令 2.1 基本操作 #1、查看空目录的git状态 $ git status fatal: not a git repository (or any of the parent directories): .git#2、初始化本地仓库:创建一个git的目录管理当前项目的所有文件版本 $ git init Initializ…...

GPU性能实时监测的实用工具
大家好,我是爱编程的喵喵。双985硕士毕业,现担任全栈工程师一职,热衷于将数据思维应用到工作与生活中。从事机器学习以及相关的前后端开发工作。曾在阿里云、科大讯飞、CCF等比赛获得多次Top名次。现为CSDN博客专家、人工智能领域优质创作者。喜欢通过博客创作的方式对所学的…...
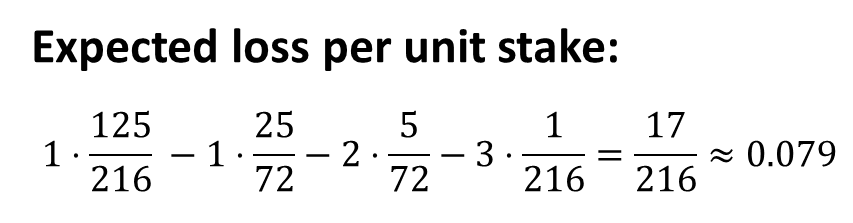
概率论中的 50 个具有挑战性的问题 [第 6 部分]:Chuck-a-Luck
一、说明 我最近对与概率有关的问题产生了兴趣。我偶然读到了弗雷德里克莫斯特勒(Frederick Mosteller)的《概率论中的五十个具有挑战性的问题与解决方案》)一书。我认为创建一个系列来讨论这些可能作为面试问题出现的迷人问题会很有趣。每篇…...

windows搭建MySQL主从补充说明
这3种情况是在HA切换时,由于是异步复制,且sync_binlog0,会造成一小部分binlog没接收完导致同步报错。 第一种:在master上删除一条记录,而slave上找不到。 第二种:主键重复。在slave已经有该记录ÿ…...

Python:GUI Tkinter
GUI编程 GUI编程(Graphical User Interface Programming)指的是用于创建图形用户界面的程序设计。这种界面采用图形方式显示信息,让用户可以通过图形化的方式与程序进行交互,而不是仅仅通过文本命令。GUI编程使得软件更加直观易用…...

制作一个可以离线安装的Visual Studio安装包
须知 前提条件,需要电脑可以正常上网且网速还行,硬盘可以空间容量足够大,怎么判断容量够用?由组件数量的多少来决定。Visual Studio 频道和发布节奏 https://learn.microsoft.com/zh-cn/visualstudio/productinfo/release-rhythm…...
机器学习——决策树(三)
【说明】文章内容来自《机器学习——基于sklearn》,用于学习记录。若有争议联系删除。 1、案例一 决策树用于是否赖床问题。 采用决策树进行分类,要经过数据采集、特征向量化、模型训练和决策树可视化4个步骤。 赖床数据链接:https://pan…...
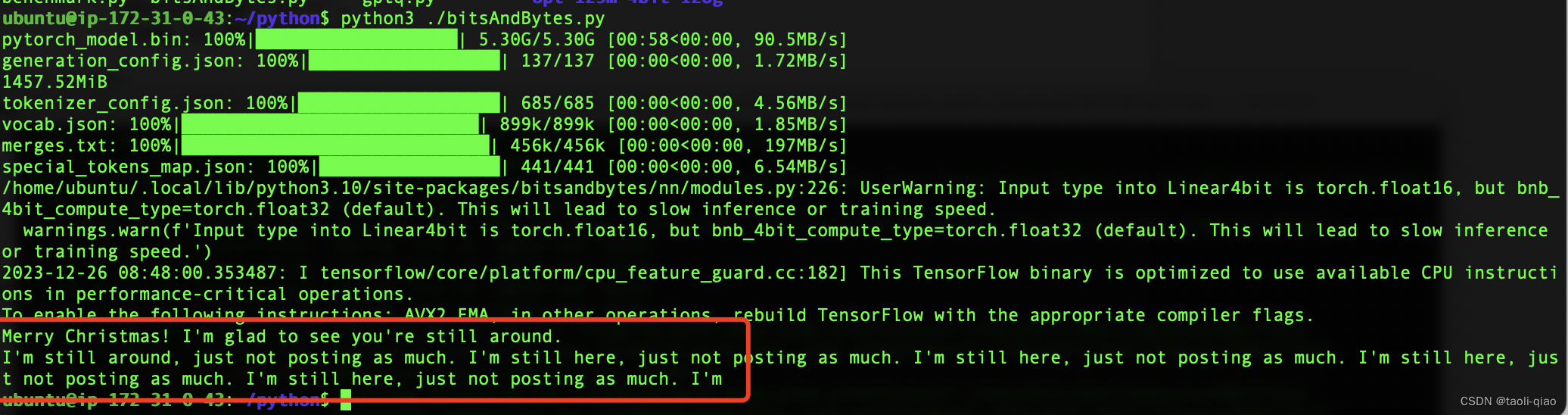
模型量化之AWQ和GPTQ
什么是模型量化 模型量化(Model Quantization)是一种通过减少模型参数表示的位数来降低模型计算和存储开销的技术。一般来说,模型参数在深度学习模型中以浮点数(例如32位浮点数)的形式存储,而模型量化可以…...
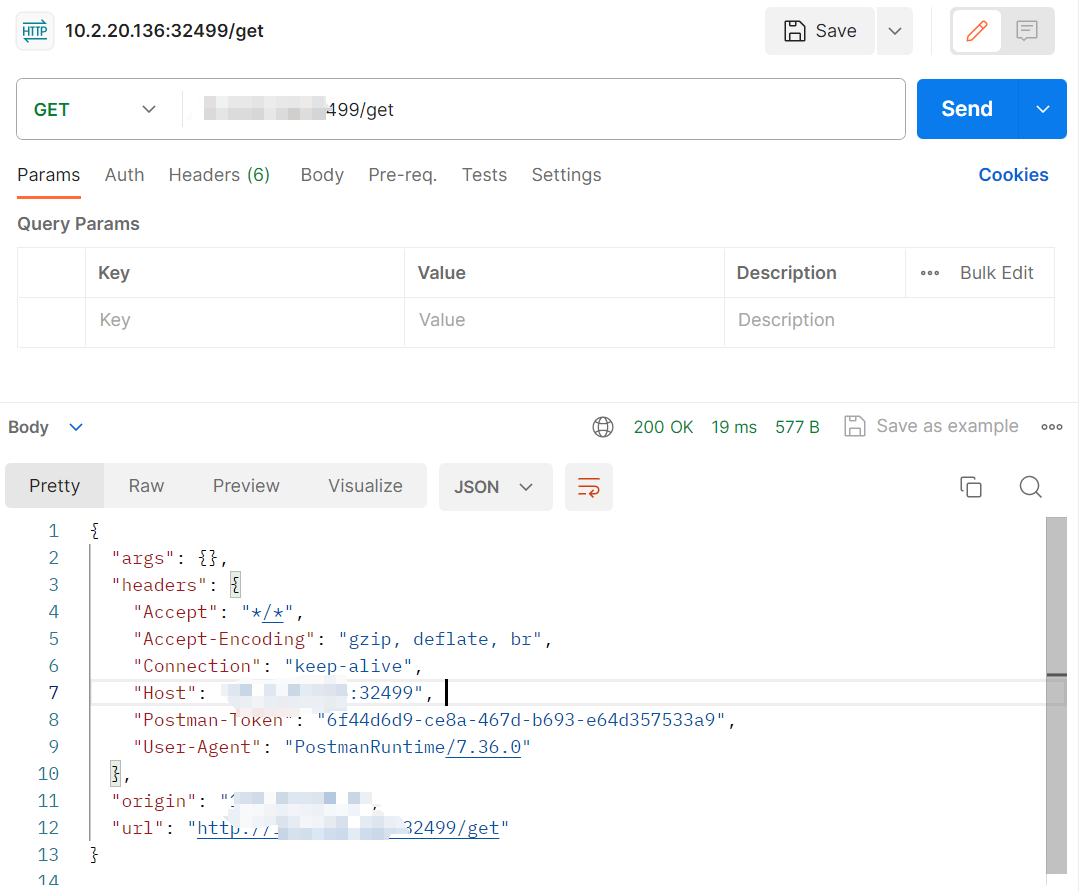
一个简单的 HTTP 请求和响应服务——httpbin
拉取镜像 docker pull kennethreitz/httpbin:latest 查看本地是否存在存在镜像 docker images | grep kennethreitz/httpbin:latest 创建 deployment,指定镜像 apiVersion: apps/v1 kind: Deployment metadata:labels:app: httpbinname: mm-httpbinnamespace: mm-…...
赛题第3套)
2024黑龙江省职业院校技能大赛暨国赛选拔赛应用软件系统开发赛项(高职组)赛题第3套
2024黑龙江省职业院校技能大赛暨国赛选拔赛 应用软件系统开发赛项(高职组) 赛题第3套 目录: 需要竞赛源码资料可以私信博主。 竞赛说明 模块一:系统需求分析 任务1:制造执行MES—质量管理—来料检验(…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...
)
uniapp 集成腾讯云 IM 富媒体消息(地理位置/文件)
UniApp 集成腾讯云 IM 富媒体消息全攻略(地理位置/文件) 一、功能实现原理 腾讯云 IM 通过 消息扩展机制 支持富媒体类型,核心实现方式: 标准消息类型:直接使用 SDK 内置类型(文件、图片等)自…...

