【机器学习】西瓜书第6章支持向量机课后习题6.1参考答案
【机器学习】西瓜书学习心得及课后习题参考答案—第6章支持向量机
1.试证明样本空间中任意点x到超平面(w,b)的距离为式(6.2)。
首先,直观解释二维空间内点到直线的距离:

由平面向量的有关知识,可得:
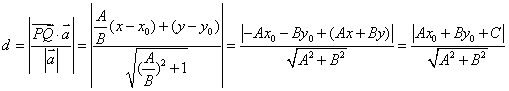
超平面的法向量为 w w w,任取平面上一点 x 0 x_0 x0,则超平面可以表示为 ω T ⋅ x 0 + b = 0 ω^T \cdot x_0 + b = 0 ωT⋅x0+b=0。一个点 x x x到超平面的距离可以用该点到 x 0 x_0 x0 的距离在法向量 (ω) 方向上的投影来表示,即:
距离 = ∣ ω T ( x − x 0 ) ∣ ∣ ∣ ω ∣ ∣ = ∣ ω T x + b ∣ ∣ ∣ ω ∣ ∣ \text{距离} = \frac{|ω^T(x−x_0)|}{||ω||} = \frac{|ω^T x + b|}{||ω||} 距离=∣∣ω∣∣∣ωT(x−x0)∣=∣∣ω∣∣∣ωTx+b∣
其中:
- ω T ω^T ωT 表示向量 w w w 的转置。
- ∣ ∣ ω ∣ ∣ ||ω|| ∣∣ω∣∣ 表示向量 w w w 的范数(模长)。
- x x x 是指向平面上的任意点。
- x 0 x_0 x0 是平面上的某一点。
- b b b 是平面的偏置项。
这个公式表示了点 x x x 到平面的距离,计算方式是将点 x x x 投影到法向量 ω ω ω 上,然后除以 ω ω ω 的模长。
其中 ω = ( ω_1; ω_2; … ; ωd) 为法向量,决定了超平面的方向 ; b b b 为位移项,决定
了超平面与原点之间的距离.
相关文章:
【机器学习】西瓜书第6章支持向量机课后习题6.1参考答案
【机器学习】西瓜书学习心得及课后习题参考答案—第6章支持向量机 1.试证明样本空间中任意点x到超平面(w,b)的距离为式(6.2)。 首先,直观解释二维空间内点到直线的距离: 由平面向量的有关知识,可得: 超平面的法向量为 w w w&am…...

【OpenAI Q* 超越人类的自主系统】DQN :Q-Learning + 深度神经网络
深度 Q 网络:用深度神经网络,来近似Q函数 强化学习介绍离散场景,使用行为价值方法连续场景,使用概率分布方法实时反馈连续场景:使用概率分布 行为价值方法 DQN(深度 Q 网络) 深度神经网络 Q-L…...

Vue axios Post请求 403 解决之道
前言: 刚开始请求的时候报 CORS 错误,通过前端项目配置后算是解决了,然后,又开始了新的报错 403 ERR_BAD_REQUEST。但是 GET 请求是正常的。 后端的 Controller 接口代码如下: PostMapping(value "/login2&qu…...
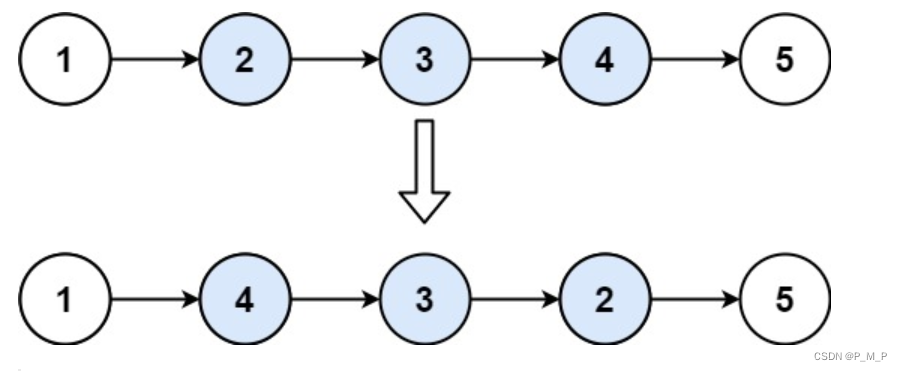
【Leetcode】重排链表、旋转链表、反转链表||
目录 💡重排链表 题目描述 方法一: 方法二: 💡旋转链表 题目描述 方法: 💡反转链表|| 题目描述 方法: 💡总结 💡重排链表 题目描述 给定一个单链表 L 的头节…...
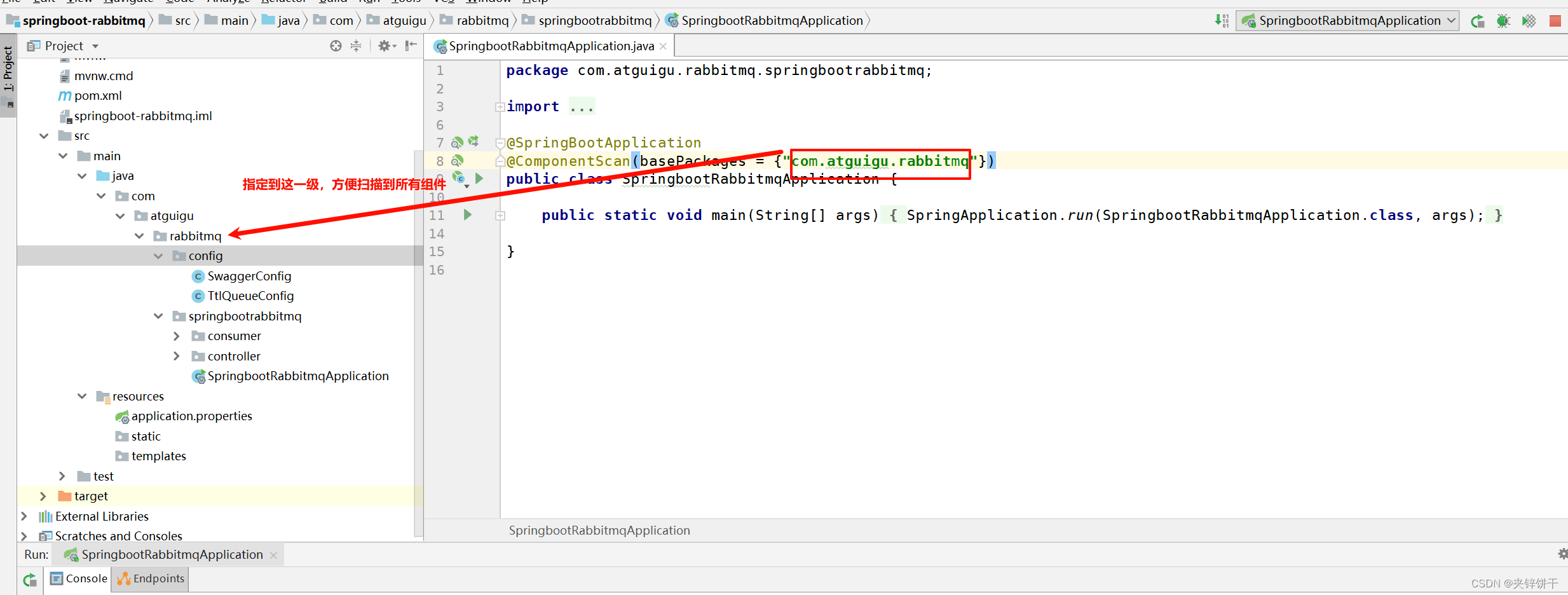
RabbitMQ 报错:Failed to declare queue(s):[QD, QA, QB]
实在没想到会犯这种低级错误。 回顾整理一下吧: 原因:SpringBoot主配置类默认只会扫描自己所在的包及其子包下面的组件。其他位置的配置不会被扫描。 如果非要使用其他位置,就需要在启动类上面指定新的扫描位置。注意新的扫描位置会覆盖默…...
Neo4j 5建库
Neo4j 只有企业版可以运行多个库,社区版无法创建多个库,一个实例只能运行一个库; 如果业务需要使用多个库怎么办呢? 就是在一个机器上部署多个实例,每个实例单独一个库名 这个库的名字我们可以自己定义; …...

鲁棒最小二乘法 拟合圆
圆拟合算法_基于huber加权的拟合圆算法-CSDN博客 首次拟合圆得到采用的上述blog中的 Ksa Fit 方法。 该方法存在干扰点时,拟合得到的结果会被干扰。 首次拟合圆的方法 因此需要针对外点增加权重因子,经过多次迭代后&…...

LeetCode——动态规划
动态规划 一、一维数组:斐波那契数列 爬楼梯70简单 dp定义: dp[i]表示爬到第i阶有多少种不同的方式 状态转移方程: dp[i] dp[i-1] dp[i-1] (每次可以爬1或2个台阶) 边界条件: dp[0] 1; dp[1] 1;&#…...

opencv和gdal的读写图片波段顺序问题
最近处理遥感影像总是不时听到 图片的波段错了,一开始不明就里,都是图片怎么就判断错了。 1、图像RGB波段顺序判断 后面和大家交流,基本上知道了一个判断标准。 一般来说,进入人眼的自然画面在计算机视觉中一般是rgb波段顺序表示…...

PyQt 打包成exe文件
参考链接 Python程序打包成.exe(史上最全面讲解)-CSDN博客 手把手教你将pyqt程序打包成exe(1)_pyqt exe-CSDN博客 PyInstaller 将DLL文件打包进exe_怎么把dll文件加到exe里-CSDN博客 自己的问题 按照教程走的话,会出现找不到“mmdeploy_ort_net.dll”文件的报错…...
)
【Web2D/3D】SVG(第二篇)
1. 前言 SVG(Scalable Vector Graphics,可缩放矢量图形)是一种使用XML描述2D图形的语言,由于SVG是基于XML(HTML也是基于XML的),因为SVG DOM中每个元素都是可以操作的,包含修改元素属…...

leetcode18. 四数之和
题目描述 给你一个由 n 个整数组成的数组 nums ,和一个目标值 target 。请你找出并返回满足下述全部条件且不重复的四元组 [nums[a], nums[b], nums[c], nums[d]] (若两个四元组元素一一对应,则认为两个四元组重复): …...
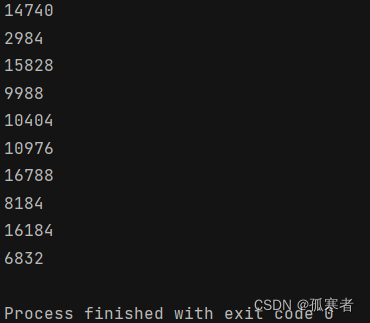
(十八)Flask之threaing.local()对象
0、引子: 如下是一段很基础的多线程代码: from threading import Threaddemo 0def task(arg):global demodemo argprint(demo)for i in range(10):t Thread(targettask, args(i, ))t. start()当程序运行时,可能会看到输出的顺序是混乱的…...
ffmpeg 硬件解码零拷贝unity 播放
ffmpeg硬件解码问题 ffmpeg 在硬件解码,一般来说,我们解码使用cuda方式,当然,最好的方式是不要确定一定是cuda,客户的显卡不一定有cuda,windows 下,和linux 下要做一些适配工作,最麻…...
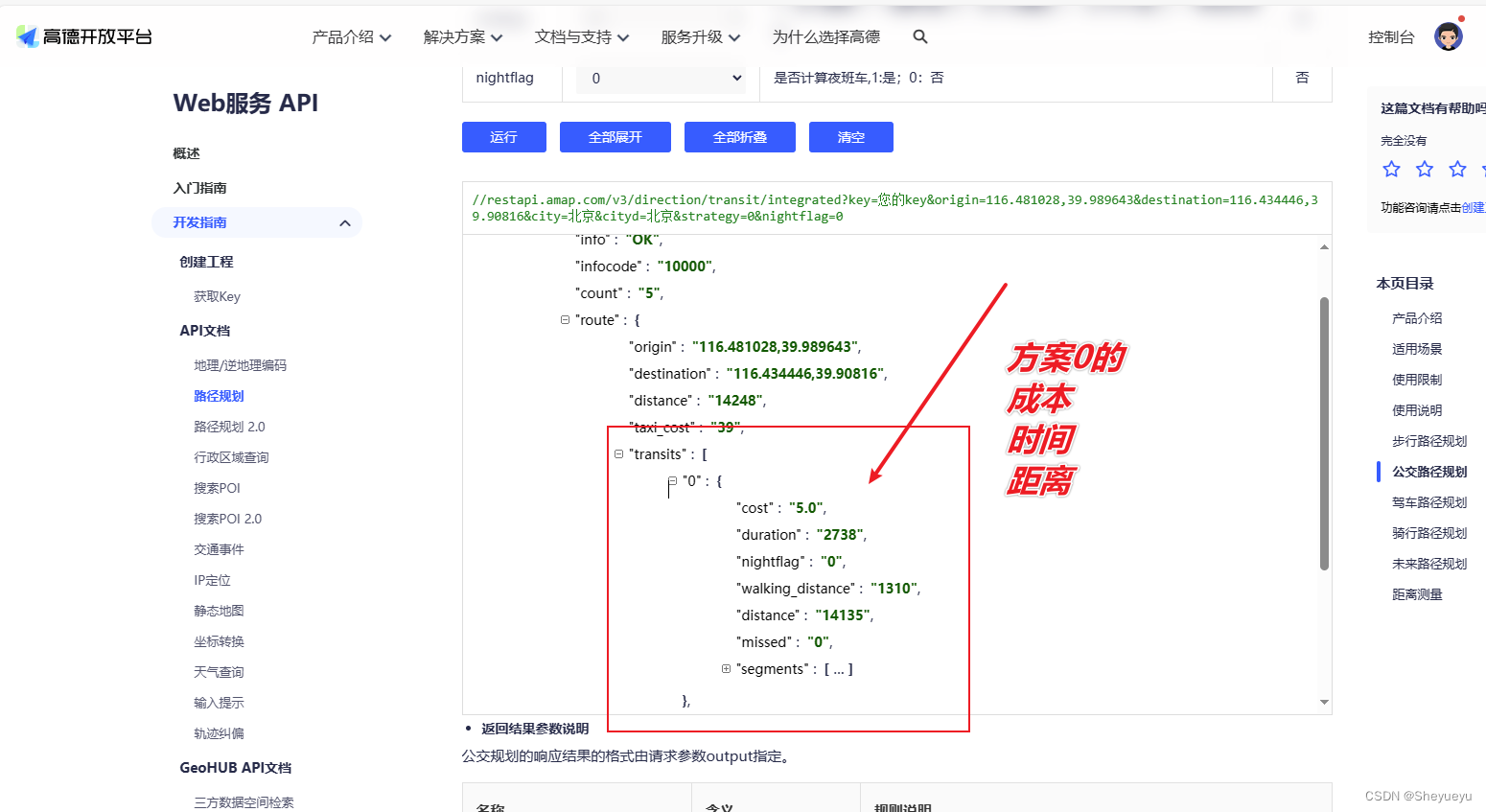
高德地图_公共交通路径规划API,获取两地点之间的驾车里程和时间
import pandas as pd import requests import jsondef get_dis_tm(origin, destination,city,cityd):url https://restapi.amap.com/v3/direction/transit/integrated?key xxx #这里就是需要去高德开放平台去申请key,请在xxxx位置填写,web服务APIlink {}origin{}&desti…...

PyTorch深度学习实战(28)——对抗攻击(Adversarial Attack)
PyTorch深度学习实战(28)——对抗攻击 0. 前言1. 对抗攻击2. 对抗攻击模型分析3. 使用 PyTorch 实现对抗攻击小结系列链接 0. 前言 近年来,深度学习在图像分类、目标检测、图像分割等诸多领域取得了突破性进展,深度学习模型已经能…...
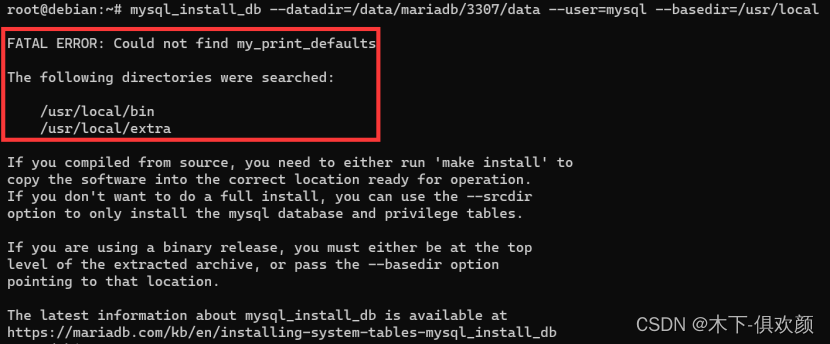
MariaDB单机多实例的配置方法
1、什么是数据库的单机多实例 数据库的单机多实例是指在一台物理服务器上运行多个数据库实例。这种部署方式允许多个数据库实例共享相同的物理资源,如CPU、内存和存储,从而提高硬件利用率并降低成本。每个数据库实例可以独立运行,处理不同的…...
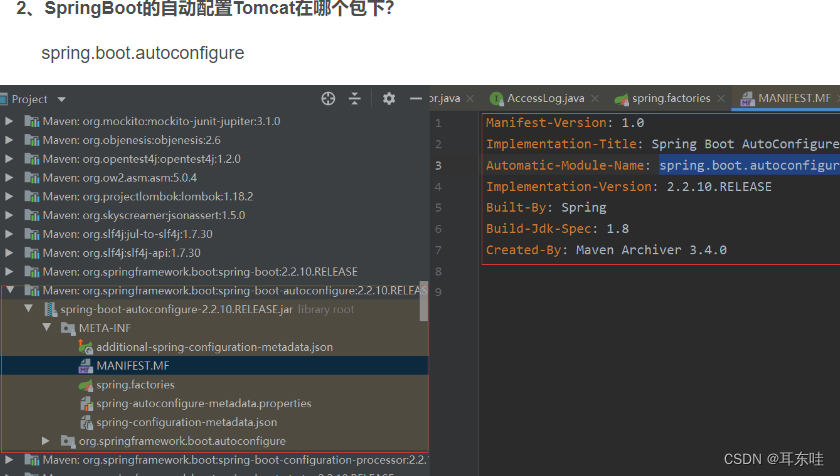
加强->servlet->tomcat
0什么是servlet jsp也是servlet 细细体会 Servlet 是 JavaEE 的规范之一,通俗的来说就是 Java 接口,将来我们可以定义 Java 类来实现这个接口,并由 Web 服务器运行 Servlet ,所以 TomCat 又被称作 Servlet 容器。 Servlet 提供了…...

Python初学者必须吃透的69个内置函数!
所谓内置函数,就是Python提供的, 可以直接拿来直接用的函数,比如大家熟悉的print,range、input等,也有不是很熟,但是很重要的,如enumerate、zip、join等,Python内置的这些函数非常精巧且强大的&…...
Day73力扣打卡
打卡记录 统计移除递增子数组的数目 II(双指针) 链接 class Solution:def incremovableSubarrayCount(self, a: List[int]) -> int:n len(a)i 0while i < n - 1 and a[i] < a[i 1]:i 1if i n - 1: # 每个非空子数组都可以移除return n …...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

【p2p、分布式,区块链笔记 MESH】Bluetooth蓝牙通信 BLE Mesh协议的拓扑结构 定向转发机制
目录 节点的功能承载层(GATT/Adv)局限性: 拓扑关系定向转发机制定向转发意义 CG 节点的功能 节点的功能由节点支持的特性和功能决定。所有节点都能够发送和接收网格消息。节点还可以选择支持一个或多个附加功能,如 Configuration …...

学习一下用鸿蒙DevEco Studio HarmonyOS5实现百度地图
在鸿蒙(HarmonyOS5)中集成百度地图,可以通过以下步骤和技术方案实现。结合鸿蒙的分布式能力和百度地图的API,可以构建跨设备的定位、导航和地图展示功能。 1. 鸿蒙环境准备 开发工具:下载安装 De…...
实现跳一跳小游戏)
鸿蒙(HarmonyOS5)实现跳一跳小游戏
下面我将介绍如何使用鸿蒙的ArkUI框架,实现一个简单的跳一跳小游戏。 1. 项目结构 src/main/ets/ ├── MainAbility │ ├── pages │ │ ├── Index.ets // 主页面 │ │ └── GamePage.ets // 游戏页面 │ └── model │ …...
