【自然语言处理】【大模型】 ΨPO:一个理解人类偏好学习的统一理论框架
论文地址:https://arxiv.org/pdf/2310.12036.pdf
相关博客
【自然语言处理】【大模型】 ΨPO:一个理解人类偏好学习的统一理论框架
【强化学习】PPO:近端策略优化算法
一、简介
通过强化学习来学习人类偏好(RLHF)主要依赖于两个重要的近似。第一个假设是成对的偏好可以被单个奖励值所替代;第二个假设是基于奖励值训练的奖励模型能够泛化到分布外的数据上。近期,DPO方法已经可以从收集的数据中直接学习策略,而不需要奖励建模阶段。然而,这个方法严重依赖于第一个假设。
本文中,试图对这些实际中的算法进行更深入的理论理解。特别地,本文推导了一个新的通用目标函数 Ψ PO \Psi\text{PO} ΨPO来从人类偏好中学习,并且绕过了两个假设。这个新的目标函数可以对RLHF和DPO的行为进行更深入的分析。
二、符号
给定上下文 x ∈ X x\in\mathcal{X} x∈X,其中 X \mathcal{X} X是有限的上下文空间,并假设 Y \mathcal{Y} Y是有限动作空间。策略 π ∈ Δ Y X \pi\in\Delta_{\mathcal{Y}}^{\mathcal{X}} π∈ΔYX会为每个上下文 x ∈ X x\in\mathcal{X} x∈X关联一个离散概率分布 π ( ⋅ ∣ x ) ∈ Δ Y \pi(\cdot|x)\in\Delta_{\mathcal{Y}} π(⋅∣x)∈ΔY,其中 Δ Y \Delta_{\mathcal{Y}} ΔY是 Y \mathcal{Y} Y上的离散分布集合。使用 μ ∈ Δ Y X \mu\in\Delta_{\mathcal{Y}}^{\mathcal{X}} μ∈ΔYX表示行为策略。对于给定的上下文 x x x, y , y ′ ∼ μ ( x ) y,y'\sim\mu(x) y,y′∼μ(x)是由行为策略独立生成的两个动作。这两个动作交由人类进行标注,标注结果表示为 y w ≻ y l y_w\succ y_l yw≻yl,其中 y w y_w yw和 y l y_l yl分别表示 { y , y ′ } \{y,y'\} {y,y′}中的偏好样本和非偏好样本。 p ∗ ( y ≻ y ′ ∣ x ) p^*(y\succ y'|x) p∗(y≻y′∣x)表示给定上下文 x x x的情况下,人类偏好 y y y优先于 y ′ y' y′的概率。之所以将其表示为概率,是因为不确定性来自于偏好产生的人的选择。因此,
p ∗ ( y ≻ y ′ ∣ x ) = E h [ I { h prefers y to y ′ give x } ] (1) p^*(y\succ y'|x)=\mathbb{E}_h[\mathbb{I}\{\text{h prefers y to }y'\text{ give x}\}] \tag{1} \\ p∗(y≻y′∣x)=Eh[I{h prefers y to y′ give x}](1)
其是关于人的期望。此外,这里也引入一个已知 x x x,生成 y y y相较于分布 μ \mu μ的期望偏好,表示为 p ∗ ( y ≻ u ∣ x ) p^*(y\succ\,u|x) p∗(y≻u∣x):
p ∗ ( y ≻ μ ∣ x ) = E y ′ ∼ μ ( ⋅ ∣ x ) [ p ∗ ( y ≻ y ′ ∣ x ) ] (2) p^*(y\succ\mu|x)=\mathbb{E}_{y'\sim\mu(\cdot|x)}[p^*(y\succ y'|x)] \tag{2} \\ p∗(y≻μ∣x)=Ey′∼μ(⋅∣x)[p∗(y≻y′∣x)](2)
对于任意的两个策略 π , μ ∈ Δ Y X \pi,\mu\in\Delta_{\mathcal{Y}}^{\mathcal{X}} π,μ∈ΔYX以及上下文分布 ρ \rho ρ,那么策略 π \pi π对于 μ \mu μ的总偏好为
p ρ ∗ ( π ≻ μ ) = E x ∼ ρ , y ∼ π ( ⋅ ∣ x ) [ p ∗ ( y ≻ μ ∣ x ) ] (3) p^*_{\rho}(\pi\succ\mu)=\mathop{\mathbb{E}}_{x\sim\rho,y\sim\pi(\cdot|x)}[p^*(y\succ\mu|x)] \tag{3}\\ pρ∗(π≻μ)=Ex∼ρ,y∼π(⋅∣x)[p∗(y≻μ∣x)](3)
实际中,无法直接观测到 p ∗ p^* p∗,仅能从具有均值 p ∗ ( y ≻ y ′ ∣ x ) p^*(y\succ y'|x) p∗(y≻y′∣x)的伯努利分布从采样 I ( y , y ′ ∣ x ) I(y,y'|x) I(y,y′∣x)。特别地,假设可以通过数据集 D = ( x i , y i , y i ′ ) i = 1 N = ( x i , y w , i ≻ y l , i ) i = 1 N \mathcal{D}=(x_i,y_i,y_i')_{i=1}^N=(x_i,y_{w,i}\succ y_{l,i})_{i=1}^N D=(xi,yi,yi′)i=1N=(xi,yw,i≻yl,i)i=1N来访问偏好,其中 N N N是数据集的尺寸。此外,对于一个一般性的有限集合 S \mathcal{S} S,一个离散概率分布 η ∈ Δ S \eta\in\Delta_{\mathcal{S}} η∈ΔS和一个实值函数 f ∈ R S f\in\mathbb{R}^{\mathcal{S}} f∈RS,那么 f f f在 η \eta η下的期望表示为 E s ∼ η [ f ( s ) ] = ∑ s ∈ S f ( s ) η ( s ) \mathbb{E}_{s\sim\eta}[f(s)]=\sum_{s\in\mathcal{S}}f(s)\eta(s) Es∼η[f(s)]=∑s∈Sf(s)η(s)。对于一个有限数据集 D = ( s i ) i = 1 N \mathcal{D}=(s_i)_{i=1}^N D=(si)i=1N,每个 s i ∈ S s_i\in\mathcal{S} si∈S且有一个实值函数 f ∈ R S f\in\mathbb{R}^{\mathcal{S}} f∈RS,那么 f f f在 D \mathcal{D} D下的经验期望为 E s ∼ D [ f ( s ) ] = 1 N ∑ i = 1 N f ( s i ) \mathbb{E}_{s\sim\mathcal{D}}[f(s)]=\frac{1}{N}\sum_{i=1}^N f(s_i) Es∼D[f(s)]=N1∑i=1Nf(si)。
三、背景知识
1. RLHF
标准RLHF范式有两个阶段:(1) 学习奖励模型;(2) 基于学习到的奖励来优化策略。
学习奖励模型。奖励模型的学习是通过训练一个区分偏好和非偏好的二分类模型,通常使用Bradley-Terry模型来构建分类模型。给定上下文 x x x,动作 y y y的奖励表示为 r ( x , y ) r(x,y) r(x,y)。Bradley-Terry模型通过对两个奖励进行sigmoid变换来表示偏好函数 p ( y ≻ y ′ ∣ x ) p(y\succ y'|x) p(y≻y′∣x):
p ( y ≻ y ′ ∣ x ) = σ ( r ( x , y ) − r ( x , y ′ ) ) (4) p(y\succ y'|x)=\sigma(r(x,y)-r(x,y')) \tag{4}\\ p(y≻y′∣x)=σ(r(x,y)−r(x,y′))(4)
其中 σ ( ⋅ ) \sigma(\cdot) σ(⋅)是sigmoid函数。给定数据集 D = ( x i , y w , i ≻ y l , i ) i = 1 N \mathcal{D}=(x_i,y_{w,i}\succ y_{l,i})_{i=1}^N D=(xi,yw,i≻yl,i)i=1N,可以通过优化下面的损失函数来学习奖励函数
L ( r ) = − E ( x , y w , y l ) ∼ D [ log ( p ( y w ≻ y l ∣ x ) ) ] (5) \mathcal{L}(r)=-\mathbb{E}_{(x,y_w,y_l)\sim\mathcal{D}}\Big[\log(p(y_w\succ y_l|x))\Big] \tag{5}\\ L(r)=−E(x,yw,yl)∼D[log(p(yw≻yl∣x))](5)
优化策略。基于奖励函数 r ( x , y ) r(x,y) r(x,y),RLHF的目标就是通过优化策略 π ∈ Δ Y X \pi\in\Delta_{\mathcal{Y}}^{\mathcal{X}} π∈ΔYX来最大化期望奖励,同时通过KL散度来最小化 π \pi π和reference策略 π ref ∈ Δ Y X \pi_{\text{ref}}\in\Delta_{\mathcal{Y}}^{\mathcal{X}} πref∈ΔYX:
J ( π ) = E π [ r ( x , y ) ] − τ D KL ( π ∥ π ref ) (6) J(\pi)=\mathbb{E}_{\pi}[r(x,y)]-\tau D_{\text{KL}}(\pi\parallel\pi_{\text{ref}}) \tag{6}\\ J(π)=Eπ[r(x,y)]−τDKL(π∥πref)(6)
其中上下文 x x x是从 ρ \rho ρ中采样的,动作 y y y是从策略 π ( ⋅ ∣ x ) \pi(\cdot|x) π(⋅∣x)采样的。散度 D KL ( π ∥ π ref ) D_{\text{KL}}(\pi\parallel\pi_{\text{ref}}) DKL(π∥πref)定义为
D KL ( π ∥ π ref ) = E x ∼ ρ [ KL ( π ( ⋅ ∣ x ) ∥ π ref ( ⋅ ∣ x ) ) ] (7) D_{\text{KL}}(\pi\parallel\pi_{\text{ref}})=\mathbb{E}_{x\sim\rho}[\text{KL}(\pi(\cdot|x)\parallel\pi_{\text{ref}}(\cdot|x))] \tag{7}\\ DKL(π∥πref)=Ex∼ρ[KL(π(⋅∣x)∥πref(⋅∣x))](7)
其中
KL ( π ( ⋅ ∣ x ) ∥ π ref ( ⋅ ∣ x ) ) = E y ∼ π ( ⋅ ∣ x ) [ log ( π ( y ∣ x ) π ref ( y ∣ x ) ) ] (8) \text{KL}(\pi(\cdot|x)\parallel\pi_{\text{ref}}(\cdot|x))=\mathbb{E}_{y\sim\pi(\cdot|x)}\Big[\log\Big(\frac{\pi(y|x)}{\pi_{\text{ref}}(y|x)}\Big)\Big] \tag{8}\\ KL(π(⋅∣x)∥πref(⋅∣x))=Ey∼π(⋅∣x)[log(πref(y∣x)π(y∣x))](8)
公式(6)的目标函数可以通过PPO来优化。RLHF+PPO在实际中取得了很好的效果。
2. DPO
一个可以替代上述RL范式的方法是直接偏好优化(DPO),其能避免训练reward模型。DPO的损失函数为
min π E ( x , y w , y l ) ∼ D [ − log σ ( τ log ( π ( y w ∣ x ) π ( y l ∣ x ) ) − τ log ( π ref ( y w ∣ x ) π ref ( y l ∣ x ) ) ) ] (9) \min_{\pi}\mathbb{E}_{(x,y_w,y_l)\sim\mathcal{D}}\Big[-\log\sigma\Big(\tau\log(\frac{\pi(y_w|x)}{\pi(y_l|x)})-\tau\log(\frac{\pi_{\text{ref}}(y_w|x)}{\pi_{\text{ref}}(y_l|x)})\Big)\Big] \tag{9}\\ πminE(x,yw,yl)∼D[−logσ(τlog(π(yl∣x)π(yw∣x))−τlog(πref(yl∣x)πref(yw∣x)))](9)
上述损失函数也可以写作
min π E x ∼ ρ ; y , y ′ ∼ μ [ − p ∗ ( y ≻ y ′ ∣ x ) log σ ( τ log ( π ( y ∣ x ) π ( y ′ ∣ x ) ) − τ log ( π ref ( y ∣ x ) π ref ( y ′ ∣ x ) ) ) ] (10) \min_{\pi}\mathop{\mathbb{E}}_{x\sim\rho;y,y'\sim\mu}\Big[-p^*(y\succ y'|x)\log\sigma\Big(\tau\log(\frac{\pi(y|x)}{\pi(y'|x)})-\tau\log(\frac{\pi_{\text{ref}}(y|x)}{\pi_{\text{ref}}(y'|x)})\Big)\Big] \tag{10}\\ πminEx∼ρ;y,y′∼μ[−p∗(y≻y′∣x)logσ(τlog(π(y′∣x)π(y∣x))−τlog(πref(y′∣x)πref(y∣x)))](10)
四、偏好优化的统一目标
本文基于最大化偏好的非线性函数构建了一个RLHF的统一目标函数。设 Ψ : [ 0 , 1 ] → R \Psi:[0,1]\rightarrow\mathbb{R} Ψ:[0,1]→R是一个非递减函数,reference策略为 π ref ∈ Δ Y X \pi_{\text{ref}}\in\Delta_{\mathcal{Y}}^{\mathcal{X}} πref∈ΔYX, τ ∈ R + ∗ \tau\in\mathbb{R}_+^* τ∈R+∗是用于正则化的正实数,那么定义 Ψ \Psi Ψ偏好优化目标函数( Ψ -preference optimisation objective , Ψ PO \Psi\text{-preference optimisation objective},\Psi\text{PO} Ψ-preference optimisation objective,ΨPO)为
max π E x ∼ ρ y ∼ π ( ⋅ ∣ x ) y ′ ∼ μ ( ⋅ ∣ x ) [ Ψ ( p ∗ ( y ≻ y ′ ∣ x ) ) ] − τ D KL ( π ∥ π ref ) (11) \max_{\pi}\mathop{\mathbb{E}}_{\substack{x\sim\rho\\y\sim\pi(\cdot|x)\\y'\sim\mu(\cdot|x)}}[\Psi(p^*(y\succ y'|x))]-\tau D_{\text{KL}}(\pi\parallel\pi_{\text{ref}}) \tag{11} \\ πmaxEx∼ρy∼π(⋅∣x)y′∼μ(⋅∣x)[Ψ(p∗(y≻y′∣x))]−τDKL(π∥πref)(11)
该目标函数在最大化偏好概率的非线性函数的同时,使用KL散度来鼓励策略接近 π ref \pi_{\text{ref}} πref。该目标函数受公式(6)启发,下面的章节会展示其能够推广至RLHF和DPO。
1. DPO和RLHF的深入分析
为了符号简单,忽略依赖 x x x。使用公式(11)的 Ψ \Psi Ψ偏好目标函数来链接DPO和RLHF。下述命题建立了这种联系
命题1。假设 Ψ ( q ) = log ( q / ( 1 − q ) ) \Psi(q)=\log(q/(1-q)) Ψ(q)=log(q/(1−q))。当Bradley-Terry模型对 p ∗ p^* p∗成立,那么就存在 r : Y → R r:\mathcal{Y}\rightarrow\mathbb{R} r:Y→R使得
p ∗ ( y ≻ y ′ ) = σ ( r ( y ) − r ( y ′ ) ) (12) p^*(y\succ y')=\sigma(r(y)-r(y'))\tag{12}\\ p∗(y≻y′)=σ(r(y)−r(y′))(12)
那么公式(11)的最优策略,公式(6)中RLHF目标函数的最优策略以及公式(10)中DPO目标函数的最优策略是相同的。
证明。在Bradley-Terry模型成立的假设下,有
E y ′ ∼ μ [ Ψ ( p ∗ ( y ≻ y ′ ) ) ] = E y ′ ∼ μ [ Ψ ( e r ( y ) e r ( y ) + e r ( y ′ ) ) ] = E y ′ ∼ μ [ log ( e r ( y ) / e r ( y ′ ) ) ] = E y ′ ∼ μ [ r ( y ) − r ( y ′ ) ] = r ( y ) − E y ′ ∼ μ [ r ( y ′ ) ] (13) \begin{align} \mathop{\mathbb{E}}_{y'\sim\mu}[\Psi(p^*(y\succ y'))]&=\mathop{\mathbb{E}}_{y'\sim\mu}\Big[\Psi\Big(\frac{e^{r(y)}}{e^{r(y)}+e^{r(y')}}\Big)\Big] \\ &=\mathop{\mathbb{E}}_{y'\sim\mu}[\log(e^{r(y)}/e^{r(y')})] \\ &=\mathop{\mathbb{E}}_{y'\sim\mu}[r(y)-r(y')] \\ &=r(y)-\mathop{\mathbb{E}}_{y'\sim\mu}[r(y')] \\ \end{align} \tag{13}\\ Ey′∼μ[Ψ(p∗(y≻y′))]=Ey′∼μ[Ψ(er(y)+er(y′)er(y))]=Ey′∼μ[log(er(y)/er(y′))]=Ey′∼μ[r(y)−r(y′)]=r(y)−Ey′∼μ[r(y′)](13)
这相当于(6)的奖励上添加一个常数。因此,公式(6)的最优策略和公式(11)的最优策略相同 。此外,在DPO的论文中已经证明了公式(6)和公式(10)具有相同的最优策略。
将该命题应用在公式(11)的目标函数,在BT假设下DPO和RLHF的封闭解可以写作
π ∗ ( y ) ∝ π ref ( y ) exp ( τ − 1 E y ′ ∼ μ [ Ψ ( p ∗ ( y ≻ y ′ ) ) ] ) (14) \pi^*(y)\propto\pi_{\text{ref}}(y)\exp\Big(\tau^{-1}\mathbb{E}_{y'\sim\mu}[\Psi(p^*(y\succ y'))]\Big) \tag{14}\\ π∗(y)∝πref(y)exp(τ−1Ey′∼μ[Ψ(p∗(y≻y′))])(14)
2. 弱正则和过拟合
偏好概率的高度非线性变换意味着偏好概率接近于1的小改进和偏好概率接近50%的大改进具有相同的激励作用。
考虑一个简单的例子,两个动作 y y y和 y ′ y' y′满足 p ∗ ( y ≻ y ′ ) = 1 p^*(y\succ y')=1 p∗(y≻y′)=1,即相比 y ′ y' y′总是偏好 y y y。Bradley-Terry模型需要 ( r ( y ) − r ( y ′ ) ) → ∞ (r(y)-r(y'))\rightarrow\infty (r(y)−r(y′))→∞来满足公式(4)。若将其插入至最优策略(14)中,无论 τ \tau τ取值为何都有
π ∗ ( y ′ ) π ∗ ( y ) = π ref ( y ′ ) π ref ( y ) exp ( τ − 1 E y ′ ∼ μ [ Ψ ( p ∗ ( y ′ ≻ y ′ ) ) − Ψ ( p ∗ ( y ≻ y ′ ) ) ] ) = π ref ( y ′ ) π ref ( y ) exp ( τ − 1 E y ′ ∼ μ [ r ( y ′ ) − r ( y ) ] ) = 0 (15) \begin{align} \frac{\pi^*(y')}{\pi^*(y)}&=\frac{\pi_{\text{ref}}(y')}{\pi_{\text{ref}}(y)}\exp\Big(\tau^{-1}\mathbb{E}_{y'\sim\mu}[\Psi(p^*(y'\succ y'))-\Psi(p^*(y\succ y'))]\Big) \\ &=\frac{\pi_{\text{ref}}(y')}{\pi_{\text{ref}}(y)}\exp(\tau^{-1}\mathbb{E}_{y'\sim\mu}[r(y')-r(y)])=0 \end{align}\tag{15} \\ π∗(y)π∗(y′)=πref(y)πref(y′)exp(τ−1Ey′∼μ[Ψ(p∗(y′≻y′))−Ψ(p∗(y≻y′))])=πref(y)πref(y′)exp(τ−1Ey′∼μ[r(y′)−r(y)])=0(15)
即 π ref ( y ′ ) = 0 \pi_{\text{ref}}(y')=0 πref(y′)=0。因此,当偏好越确定则KL正则化的效果也就越弱。
KL正则化的这种弱点在有效数据中会更加明显,因为仅能够获得偏好的样本估计 p ^ ( y ≻ y ′ ) \hat{p}(y\succ y') p^(y≻y′)。例如,即使真实的偏好时 p ∗ ( y ≻ y ′ ) = 0.8 p^*(y\succ y')=0.8 p∗(y≻y′)=0.8,但仅通过少量数据估计则很可能有 p ^ ( y ≻ y ′ ) = 1 \hat{p}(y\succ y')=1 p^(y≻y′)=1。这种情况下,对于任意的 τ \tau τ,经验最优策略将会有 π ( y ′ ) = 0 \pi(y')=0 π(y′)=0。这也意味着模型很可能会过拟合。
*为什么标准的RLHF对这个问题更加鲁棒呢?*DPO虽然能够避免拟合奖励函数,但是在真实实践中,当经验偏好的概率位于集合 { 0 , 1 } \{0,1\} {0,1}中,奖励函数通常是欠拟合的。位于 { 0 , 1 } \{0,1\} {0,1}的偏好概率的最优奖励是无限的,但是可以避免取到这些值。奖励函数的欠拟合对于获得最终策略至关重要,DPO虽然避免了奖励函数的训练,但也损失了欠拟合奖励函数带来的策略正则化。
五、IPO:基于恒等映射的 Ψ PO \Psi\text{PO} ΨPO
DPO虽然能够避免奖励函数的训练,但是容易过拟合。基于对DPO的分析,需要确保公式(11)中的KL正则化在偏好为 { 0 , 1 } \{0,1\} {0,1}的情况下仍然有效。因此,考虑公式(11)中的 Ψ \Psi Ψ为恒等映射,那么就能直接正则化总偏好:
max π p ρ ∗ ( π ≻ μ ) − τ D KL ( π ∥ π ref ) (16) \max_{\pi}p^*_{\rho}(\pi\succ\mu)-\tau D_{\text{KL}}(\pi\parallel\pi_{\text{ref}}) \tag{16}\\ πmaxpρ∗(π≻μ)−τDKL(π∥πref)(16)
优化公式(14)的标准方法是RLFH,但是使用强化学习并估计奖励模型的成本高昂。受DPO启发,能够为公式(16)求解一个经验解来避免强化学习和奖励模型。
1. 推导
寻根问题。令 g ( y ) = E y ′ ∼ μ [ Ψ ( p ∗ ( y ≻ y ′ ) ) ] g(y)=\mathbb{E}_{y'\sim\mu}[\Psi(p^*(y\succ y'))] g(y)=Ey′∼μ[Ψ(p∗(y≻y′))],然后有
π ∗ ( y ) ∝ π ref ( y ) exp ( τ − 1 g ( y ) ) (17) \pi^*(y)\propto\pi_{\text{ref}}(y)\exp(\tau^{-1}g(y)) \tag{17}\\ π∗(y)∝πref(y)exp(τ−1g(y))(17)
对于任意 y , y ′ ∈ Supp ( π ref ) y,y'\in\text{Supp}(\pi_{\text{ref}}) y,y′∈Supp(πref),我们有
π ∗ ( y ) π ∗ ( y ′ ) = π ref ( y ) π ref ( y ′ ) exp ( τ − 1 ( g ( y ) − g ( y ′ ) ) ) (18) \frac{\pi^*(y)}{\pi^*(y')}=\frac{\pi_{\text{ref}}(y)}{\pi_{\text{ref}}(y')}\exp\Big(\tau^{-1}(g(y)-g(y'))\Big) \tag{18}\\ π∗(y′)π∗(y)=πref(y′)πref(y)exp(τ−1(g(y)−g(y′)))(18)
令
h ∗ ( y , y ′ ) = log ( π ∗ ( y ) π ref ( y ′ ) π ∗ ( y ′ ) π ref ( y ) ) (19) h^*(y,y')=\log\Big(\frac{\pi^*(y)\pi_{\text{ref}}(y')}{\pi^*(y')\pi_{\text{ref}}(y)}\Big)\tag{19} \\ h∗(y,y′)=log(π∗(y′)πref(y)π∗(y)πref(y′))(19)
那么公式(18)可以重排为
h ∗ ( y , y ′ ) = τ − 1 ( g ( y ) − g ( y ′ ) ) (20) h^*(y,y')=\tau^{-1}(g(y)-g(y'))\tag{20} \\ h∗(y,y′)=τ−1(g(y)−g(y′))(20)
那么对于策略 π \pi π,定义有
h π ( y , y ′ ) = log ( π ( y ) π ref ( y ′ ) π ( y ′ ) π ref ( y ) ) (21) h_{\pi}(y,y')=\log\Big(\frac{\pi(y)\pi_{\text{ref}}(y')}{\pi(y')\pi_{\text{ref}}(y)}\Big)\tag{21} \\ hπ(y,y′)=log(π(y′)πref(y)π(y)πref(y′))(21)
而目标是求解等式
h π ( y , y ′ ) = τ − 1 ( g ( y ) − g ( y ′ ) ) (22) h_{\pi}(y,y')=\tau^{-1}(g(y)-g(y'))\tag{22} \\ hπ(y,y′)=τ−1(g(y)−g(y′))(22)
若 Ψ \Psi Ψ为恒等函数,公式(22)为
h π ( y , y ′ ) = τ − 1 ( p ∗ ( y ≻ μ ) − p ∗ ( y ′ ≻ μ ) ) (23) h_{\pi}(y,y')=\tau^{-1}\Big(p^*(y\succ\mu)-p^*(y'\succ\mu)\Big)\tag{23}\\ hπ(y,y′)=τ−1(p∗(y≻μ)−p∗(y′≻μ))(23)
寻找问题可以表达为单个最优化问题 L ( π ) L(\pi) L(π)
L ( π ) = E y , y ′ ∼ μ [ ( h π ( y , y ′ ) − p ∗ ( y ≻ μ ) − p ∗ ( y ′ ≻ μ ) τ ) 2 ] (24) L(\pi)=\mathop{\mathbb{E}}_{y,y'\sim\mu}\Big[\Big(h_{\pi}(y,y')-\frac{p^*(y\succ\mu)-p^*(y'\succ\mu)}{\tau}\Big)^2\Big]\tag{24} \\ L(π)=Ey,y′∼μ[(hπ(y,y′)−τp∗(y≻μ)−p∗(y′≻μ))2](24)
显然, L ( π ∗ ) = 0 L(\pi^*)=0 L(π∗)=0,即 π ∗ \pi^* π∗是 L ( π ) L(\pi) L(π)的全局最小值。
定理2. 假设 Supp ( μ ) = Supp ( π ref ) \text{Supp}(\mu)=\text{Supp}(\pi_{\text{ref}}) Supp(μ)=Supp(πref),并定义 Π \Pi Π为满足 Supp ( π ) = Supp ( μ ) \text{Supp}(\pi)=\text{Supp}(\mu) Supp(π)=Supp(μ)的策略 π \pi π的集合。那么 π → L ( π ) \pi\rightarrow L(\pi) π→L(π)在集合 Π \Pi Π上有唯一的局部/全局最小值 π ∗ \pi^* π∗。
证明。根据假设 π ∗ ∈ Π \pi^*\in\Pi π∗∈Π以及定义 ∀ π ∈ Π \forall\pi\in\Pi ∀π∈Π,以及由于 L ( π ) L(\pi) L(π)是平方项的期望,所以 L ( π ) ≥ 0 L(\pi)\geq 0 L(π)≥0。根据公式(20)可知 L ( π ∗ ) = 0 L(\pi^*)=0 L(π∗)=0,因此可以推断出 π ∗ \pi^* π∗是 L L L的全局最优值。下面将展示 L L L在 Π \Pi Π中没有其他局部/全局最小值。
记 J = Supp ( μ ) J=\text{Supp}(\mu) J=Supp(μ)。通过logits 向量 s ∈ R J s\in\mathbb{R}^{J} s∈RJ来参数化集合 Π \Pi Π,对于 y ∈ J y\in J y∈J令 π s ( y ) = exp ( s ( y ) ) / ∑ y ′ ∈ J exp ( s ( y ′ ) ) \pi_s(y)=\exp(s(y))/\sum_{y'\in J}\exp(s(y')) πs(y)=exp(s(y))/∑y′∈Jexp(s(y′)),否则 π s ( y ) = 0 \pi_s(y)=0 πs(y)=0。令 L ( s ) = L ( π s ) \mathcal{L}(s)=L(\pi_s) L(s)=L(πs)是logits s s s的目标函数。
L ( s ) = E y , y ′ ∼ μ [ [ p ∗ ( y ≻ μ ) − p ∗ ( y ′ ≻ μ ) τ − ( s ( y ) − s ( y ′ ) ) − log ( π ref ( y ′ ) π ref ( y ) ) ] 2 ] (25) \mathcal{L}(s)=\mathbb{E}_{y,y'\sim\mu}\Big[\Big[ \frac{p^*(y\succ\mu)-p^*(y'\succ\mu)}{\tau}-(s(y)-s(y'))-\log\Big(\frac{\pi_{\text{ref}}(y')}{\pi_{\text{ref}}(y)}\Big) \Big]^2\Big]\tag{25} \\ L(s)=Ey,y′∼μ[[τp∗(y≻μ)−p∗(y′≻μ)−(s(y)−s(y′))−log(πref(y)πref(y′))]2](25)
目标函数是logits s s s的二次函数。此外,通过展开上面的二次函数,损失值可以表达为平方项之和
∑ y , y ′ ∈ J μ ( y ) μ ( y ′ ) ( s ( y ) − s ( y ′ ) ) 2 (26) \sum_{y,y'\in J}\mu(y)\mu(y')(s(y)-s(y'))^2\tag{26} \\ y,y′∈J∑μ(y)μ(y′)(s(y)−s(y′))2(26)
因此这是一个半正定二次函数,因此是凸的。因此可以推断出损失函数 L ( s ) \mathcal{L}(s) L(s)的所有局部最小值即为全局最小值。 π s \pi_s πs是从 s s s到 π \pi π的满连续映射,可以很容易的证明 L L L的每个局部最小值 π \pi π都对于于 L \mathcal{L} L的局部最小值 S π \mathcal{S}_{\pi} Sπ。因此, L L L的所有局部最小值都是全局最小值。
2. IPO的采样损失
为了能够获得IPO的采样损失值,需要对公式(24)右侧进行无偏估计。为了这个目标,考虑Population IPO Loss
E y , y ′ ∼ μ [ ( h π ( y , y ′ ) − τ − 1 I ( y , y ′ ) ) 2 ] (27) \mathbb{E}_{y,y'\sim\mu}\Big[(h_{\pi}(y,y')-\tau^{-1}I(y,y'))^2\Big]\tag{27} \\ Ey,y′∼μ[(hπ(y,y′)−τ−1I(y,y′))2](27)
其中 I ( y , y ′ ) I(y,y') I(y,y′)是从均值为 p ∗ ( y ≻ y ′ ) p^*(y\succ y') p∗(y≻y′)的伯努利分布中采样的,即相比于 y ′ y' y′更偏好 y y y时 I ( y , y ′ ) I(y,y') I(y,y′)为1,否则为0。这样就能直接获得一个可用的基于采样的损失值,通过从偏好数据集中采样 ( y , y ′ ) (y,y') (y,y′)并查询记录来获得 I ( y , y ′ ) I(y,y') I(y,y′)。下面的命题将证明公式(24)到公式(27)的变换是等价的。
命题3。公式(24)与公式(27)是等价的。
证明。这个等价并不是很显然的,因为通常情况下的条件期望为
E [ h π ( Y , Y ′ ) − τ − 1 I ( Y , Y ′ ) ∣ Y = y , Y ′ = y ′ ] \mathbb{E}[h_{\pi}(Y,Y')-\tau^{-1}I(Y,Y')|Y=y,Y'=y'] \\ E[hπ(Y,Y′)−τ−1I(Y,Y′)∣Y=y,Y′=y′]
并不等于公式(24)对应的值,即
h π ( y , y ′ ) − τ − 1 ( p ∗ ( y ≻ μ ) − p ∗ ( y ′ ≻ μ ) ) h_{\pi}(y,y')-\tau^{-1}(p^*(y\succ\mu)-p^*(y'\succ\mu)) \\ hπ(y,y′)−τ−1(p∗(y≻μ)−p∗(y′≻μ))
相反,我们需要利用分布 y y y和 y ′ y' y′的一些对称性,并使用 h π ( y , y ′ ) h_{\pi}(y,y') hπ(y,y′)能够分解为 y y y和 y ′ y' y′的加性函数的事实。为了说明损失值的相等性,仅关注公式(24)和(27)中交叉项就足够了,也就是满足
E y , y ′ ∼ μ [ h π ( y , y ′ ) I ( y , y ′ ) ] = E y , y ′ ∼ μ [ h π ( y , y ′ ) ( p ∗ ( y ≻ μ ) − p ∗ ( y ′ ≻ μ ) ) ] \begin{align} \mathbb{E}_{y,y'\sim\mu}\Big[h_{\pi}(y,y')I(y,y')\Big] =\mathbb{E}_{y,y'\sim\mu}\Big[h_{\pi}(y,y')(p^*(y\succ\mu)-p^*(y'\succ\mu))\Big] \end{align} \\ Ey,y′∼μ[hπ(y,y′)I(y,y′)]=Ey,y′∼μ[hπ(y,y′)(p∗(y≻μ)−p∗(y′≻μ))]
为了简洁使用 π y = log ( π ( y ) ) , π y R = log ( π ref ( y ) ) , p y = p ∗ ( y ≻ μ ) \pi_y=\log(\pi(y)),\pi_y^R=\log(\pi_{\text{ref}}(y)),p_y=p^*(y\succ\mu) πy=log(π(y)),πyR=log(πref(y)),py=p∗(y≻μ),右侧有
E y , y ′ ∼ μ [ h π ( y , y ′ ) ( p ∗ ( y ≻ μ ) − p ∗ ( y ′ ≻ μ ) ) ] = E y , y ′ ∼ μ [ ( π y − π y ′ + π y ′ R − π y R ) ( p y − p y ′ ) ] = E y , y ′ ∼ μ [ π y p y − π y p y ′ − π y ′ p y + π y ′ + p y ′ + π y ′ R p y − π y ′ R p y ′ − π y R p y + π y R p y ′ ] = E y , y ′ ∼ μ [ ( 2 p y − 1 ) π y − ( 2 p y − 1 ) π y R ] \begin{align} &\mathbb{E}_{y,y'\sim\mu}\Big[h_{\pi}(y,y')(p^*(y\succ\mu)-p^*(y'\succ\mu))\Big] \\ =&\mathbb{E}_{y,y'\sim\mu}\Big[(\pi_y-\pi_{y'}+\pi_{y'}^R-\pi_{y}^R)(p_y-p_{y'})\Big] \\ =&\mathbb{E}_{y,y'\sim\mu}\Big[\pi_y p_y-\pi_y p_{y'}-\pi_{y'} p_y+\pi_{y'}+p_{y'}+\pi_{y'}^R p_y-\pi_{y'}^R p_{y'}-\pi_{y}^R p_y+\pi_{y}^R p_{y'}\Big] \\ =&\mathbb{E}_{y,y'\sim\mu}\Big[(2p_y-1)\pi_{y}-(2p_y-1)\pi_{y}^R\Big] \end{align} \\ ===Ey,y′∼μ[hπ(y,y′)(p∗(y≻μ)−p∗(y′≻μ))]Ey,y′∼μ[(πy−πy′+πy′R−πyR)(py−py′)]Ey,y′∼μ[πypy−πypy′−πy′py+πy′+py′+πy′Rpy−πy′Rpy′−πyRpy+πyRpy′]Ey,y′∼μ[(2py−1)πy−(2py−1)πyR]
其中使用了 y y y和 y ′ y' y′的独立同分布且 E y ∼ μ [ p y ] = 1 / 2 E_{y\sim\mu}[p_y]=1/2 Ey∼μ[py]=1/2。左侧有
E y , y ′ ∼ μ [ h π ( y , y ′ ) I ( y , y ′ ) ] = E y , y ′ ∼ μ [ ( π y − π y ′ + π y ′ R − π y R ) I ( y , y ′ ) ] = E y ∼ μ [ ( π y − π y R ) E y ′ ∼ μ [ I ( y , y ′ ) ∣ y ] ] + E y ′ ∼ μ [ ( − π y ′ + π y ′ R E y ∼ μ [ I ( y , y ′ ) ∣ y ′ ] ) ] = E y , y ′ ∼ μ [ π y p y − π y ′ ( 1 − p y ′ ) + π y ′ R ( 1 − p y ′ ) − π y R p y ] = E y , y ′ ∼ μ [ ( 2 p y − 1 ) π y − ( 2 p y − 1 ) π y R ] \begin{align} &\mathbb{E}_{y,y'\sim\mu}\Big[h_{\pi}(y,y')I(y,y')\Big]\\ =&\mathbb{E}_{y,y'\sim\mu}\Big[(\pi_y-\pi_{y'}+\pi_{y'}^R-\pi_y^R)I(y,y')\Big] \\ =&\mathbb{E}_{y\sim\mu}\Big[(\pi_y-\pi_y^R)\mathbb{E}_{y'\sim\mu}[I(y,y')|y]\Big]+\mathbb{E}_{y'\sim\mu}\Big[(-\pi_{y'}+\pi_{y'}^R\mathbb{E}_{y\sim\mu}[I(y,y')|y'])\Big] \\ =&\mathbb{E}_{y,y'\sim\mu}\Big[\pi_y p_y-\pi_{y'}(1-p_{y'})+\pi_{y'}^R(1-p_{y'})-\pi_y^R p_y\Big] \\ =&\mathbb{E}_{y,y'\sim\mu}\Big[(2p_y-1)\pi_y-(2p_y-1)\pi_{y}^R\Big] \end{align} \\ ====Ey,y′∼μ[hπ(y,y′)I(y,y′)]Ey,y′∼μ[(πy−πy′+πy′R−πyR)I(y,y′)]Ey∼μ[(πy−πyR)Ey′∼μ[I(y,y′)∣y]]+Ey′∼μ[(−πy′+πy′REy∼μ[I(y,y′)∣y′])]Ey,y′∼μ[πypy−πy′(1−py′)+πy′R(1−py′)−πyRpy]Ey,y′∼μ[(2py−1)πy−(2py−1)πyR]
其中使用了 E y ′ ∼ μ I ( y , y ′ ) = p y \mathbb{E}_{y'\sim\mu}I(y,y')=p_y Ey′∼μI(y,y′)=py和 E y ∼ μ I ( y , y ′ ) = 1 − p y ′ \mathbb{E}_{y\sim\mu}I(y,y')=1-p_{y'} Ey∼μI(y,y′)=1−py′。这样就证明了两个损失值的相等性。
接下来讨论如何使用数据集来近似等式(27)的损失值。数据集 D \mathcal{D} D的形式为 ( y w , i , y l , i ) i = 1 N (y_{w,i},y_{l,i})_{i=1}^N (yw,i,yl,i)i=1N。每个数据点 ( y w , i , y l , i ) (y_{w,i},y_{l,i}) (yw,i,yl,i)都能为等式(27)贡献两项经验近似,即 ( y , y ′ , I ( y , y ′ ) ) = ( y w , i , y l , i , 1 ) (y,y',I(y,y'))=(y_{w,i},y_{l,i},1) (y,y′,I(y,y′))=(yw,i,yl,i,1)和 ( y , y ′ , I ( y , y ′ ) ) = ( y l , i , y w , i , 0 ) (y,y',I(y,y'))=(y_{l,i},y_{w,i},0) (y,y′,I(y,y′))=(yl,i,yw,i,0)。利用这种对称性是很重要的,因为其可以降低损失值的方差。总体的经验损失为
1 2 E y w , y l ∼ D [ ( h π ( y w , y l ) − τ − 1 ) 2 + h π ( y l , y w ) 2 ] = 1 2 E y w , y l ∼ D [ ( h π ( y w , y l ) − τ − 1 ) 2 + h π ( y w , y l ) 2 ] \begin{align} &\frac{1}{2}\mathbb{E}_{y_w,y_l\sim D}\Big[(h_{\pi}(y_w,y_l)-\tau^{-1})^2+h_{\pi}(y_l,y_w)^2\Big] \\ =&\frac{1}{2}\mathbb{E}_{y_w,y_l\sim D}\Big[(h_{\pi}(y_w,y_l)-\tau^{-1})^2+h_{\pi}(y_w,y_l)^2\Big] \end{align} \\ =21Eyw,yl∼D[(hπ(yw,yl)−τ−1)2+hπ(yl,yw)2]21Eyw,yl∼D[(hπ(yw,yl)−τ−1)2+hπ(yw,yl)2]
其等于
E y w , y l ∼ D [ ( h π ( y w , y l ) − τ − 1 2 ) 2 ] (28) \mathbb{E}_{y_w,y_l\sim D}\Big[\Big(h_{\pi}(y_w,y_l)-\frac{\tau^{-1}}{2}\Big)^2\Big] \tag{28}\\ Eyw,yl∼D[(hπ(yw,yl)−2τ−1)2](28)
这种损失函数的简化形式能够为IPO优化策略 π \pi π提供一些有价值的洞见:IPO通过回归对数似然 log ( π ( y w ) / π ( y l ) ) \log(\pi(y_w)/\pi(y_l)) log(π(yw)/π(yl))和 log ( π ref ( y w ) / π ref ( y l ) ) \log(\pi_{\text{ref}}(y_w)/\pi_{\text{ref}}(y_l)) log(πref(yw)/πref(yl))之间的差距至 τ − 1 2 \frac{\tau^{-1}}{2} 2τ−1来从偏好数据集中学习。所以当正则化越弱,则 y w y_w yw对 y l y_l yl的对数似然率也越高。不同于DPO,IPO通过控制 log ( π ( y w ) / π ( y l ) ) \log(\pi(y_w)/\pi(y_l)) log(π(yw)/π(yl))和 log ( π ref ( y w ) / π ref ( y l ) ) \log(\pi_{\text{ref}}(y_w)/\pi_{\text{ref}}(y_l)) log(πref(yw)/πref(yl))之间的差距来正则化,从而避免了偏好数据集的过拟合。
完整的IPO算法为
数据集 D = ( y w , i , y l , i ) i = 1 N \mathcal{D}=(y_{w,i},y_{l,i})_{i=1}^N D=(yw,i,yl,i)i=1N;reference策略 π ref \pi_{\text{ref}} πref;
定义
h π ( y , y ′ , x ) = log ( π ( y ∣ x ) π ref ( y ′ ∣ x ) π ( y ′ ∣ x ) π ref ( y ∣ x ) ) h_{\pi}(y,y',x)=\log\Big(\frac{\pi(y|x)\pi_{\text{ref}}(y'|x)}{\pi(y'|x)\pi_{\text{ref}}(y|x)}\Big) \\ hπ(y,y′,x)=log(π(y′∣x)πref(y∣x)π(y∣x)πref(y′∣x))开始于 π = π ref \pi=\pi_{\text{ref}} π=πref,最小化
E y w , y l , x ∼ D ( h π ( y w , y l , x ) − τ − 1 2 ) 2 \mathbb{E}_{y_w,y_l,x\sim D}\Big(h_{\pi}(y_w,y_l,x)-\frac{\tau^{-1}}{2}\Big)^2 \\ Eyw,yl,x∼D(hπ(yw,yl,x)−2τ−1)2
3. 样例分析
考虑最简单的情况,仅有两个动作 y 1 y_1 y1和 y 2 y_2 y2,且二者偏好明确 p ∗ ( y 1 ≻ y 2 ) = 1 p^*(y_1\succ y_2)=1 p∗(y1≻y2)=1。假设 π ref \pi_{\text{ref}} πref和 μ \mu μ是相同。对于DPO来说,无论 τ \tau τ取何值都有 π ∗ ( y 1 ) = 1 , π ∗ ( y 2 ) = 0 \pi^*(y_1)=1,\pi^*(y_2)=0 π∗(y1)=1,π∗(y2)=0。即使正则化系数 τ \tau τ非常大,仍然会导致于 π ref \pi_{\text{ref}} πref非常不同。
对于IPO来说,有 p ∗ ( y 1 ≻ μ ) = 3 / 4 p^*(y_1\succ\mu)=3/4 p∗(y1≻μ)=3/4且 p ∗ ( y 2 ≻ μ ) = 1 / 4 p^*(y_2\succ\mu)=1/4 p∗(y2≻μ)=1/4。将其插入至公式(17)且 Ψ = I \Psi=I Ψ=I,那么有 π ∗ ( y 1 ) = σ ( 0.5 τ − 1 ) \pi^*(y_1)=\sigma(0.5\tau^{-1}) π∗(y1)=σ(0.5τ−1)且 π ∗ ( y 2 ) = σ ( − 0.5 τ − 1 ) \pi^*(y_2)=\sigma(-0.5\tau^{-1}) π∗(y2)=σ(−0.5τ−1)。因此,正则化系数 τ → + ∞ \tau\rightarrow+\infty τ→+∞,则 π ∗ \pi^* π∗则收敛至 π ref \pi_{\text{ref}} πref。当 τ → + 0 \tau\rightarrow+0 τ→+0,那么有 π ∗ ( y 1 ) → 1 \pi^*(y_1)\rightarrow 1 π∗(y1)→1且 π ∗ ( y 2 ) → 0 \pi^*(y_2)\rightarrow 0 π∗(y2)→0。正则化系数 τ \tau τ可以用来控制与 π ref \pi_{\text{ref}} πref的接近程度。
相关文章:

【自然语言处理】【大模型】 ΨPO:一个理解人类偏好学习的统一理论框架
一个理解人类偏好学习的统一理论框架 《A General Theoretical Paradiam to Understand Learning from Human Preferences》 论文地址:https://arxiv.org/pdf/2310.12036.pdf 相关博客 【自然语言处理】【大模型】 ΨPO:一个理解人类偏好学习的统一理论框…...
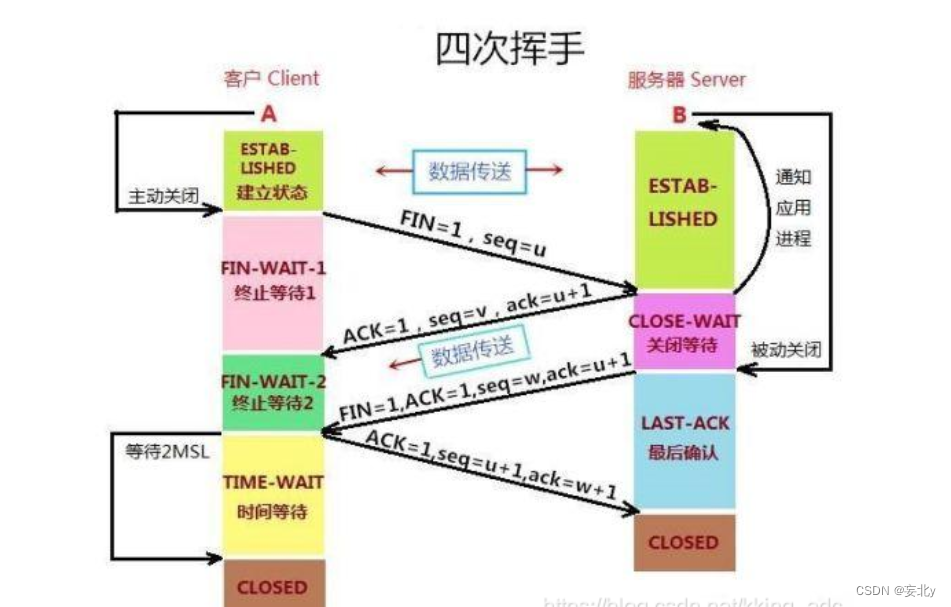
计算机网络——传输层(五)
前言: 最重要的网络层我们已经学习完了,下面让我们再往上一层,对网络层的上一层传输层进行一个学习与了解,学习网络层的基本概念和网络层中的TCP协议和UDP协议 目录 编辑一、传输层的概述: 1.传输层: …...
python3处理docx并flask显示
前言: 最近有需求处理docx文件,并讲内容显示到页面,对world进行在线的阅读,这样我这里就使用flaskDocument对docx文件进行处理并显示,下面直接上代码: Document处理: 首先下载Document的库文…...
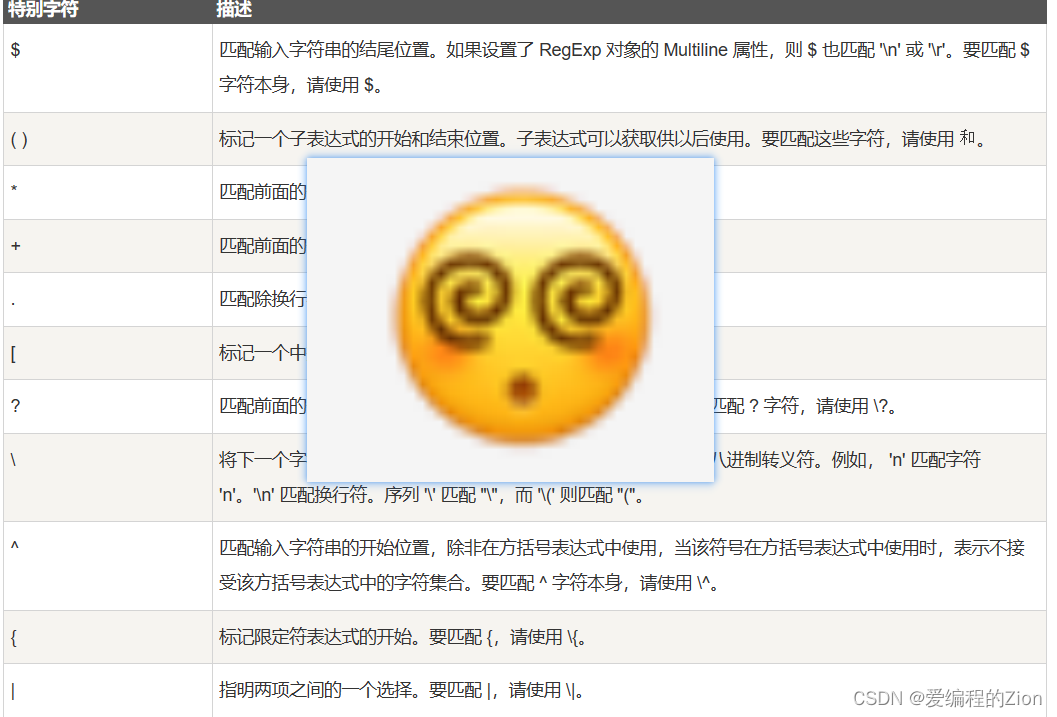
Python:正则表达式速通,码上上手!
1前言 正则表达式(Regular Expression)是一种用来描述字符串模式的表达式。它是一种强大的文本匹配工具,可以用来搜索、替换和提取符合特定模式的文本。 正则表达式由普通字符(例如字母、数字、符号等)和元字符&#…...
centos7安装nginx并安装部署前端
目录: 一、安装nginx第一种方式(外网)第二种方式(内网) 二、配置前端项目三、Nginx相关命令 好久不用再次使用生疏,这次记录一下 一、安装nginx 第一种方式(外网) 1、下载nginx ng…...
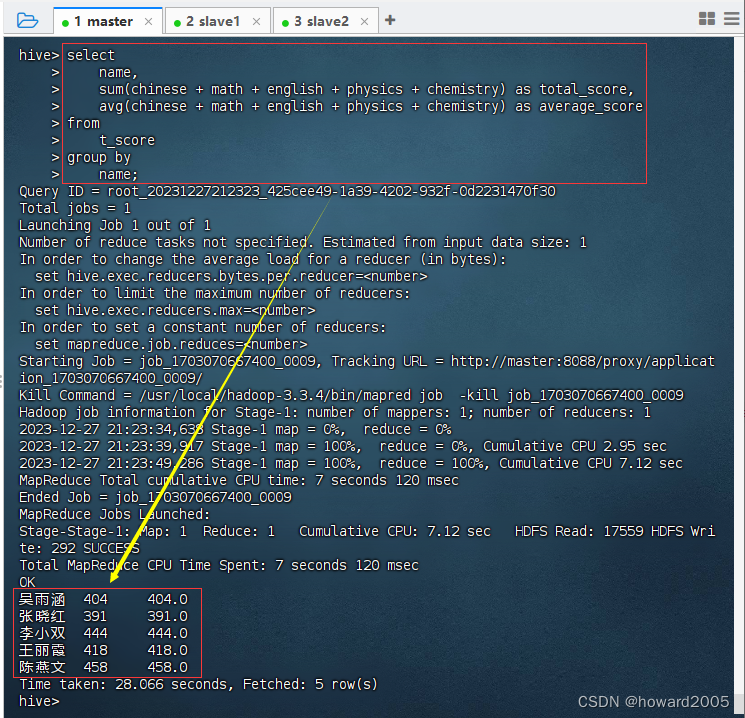
Hive实战:统计总分与平均分
文章目录 一、实战概述二、提出任务三、完成任务(一)准备数据文件1、在虚拟机上创建文本文件2、将文本文件上传到HDFS指定目录 (二)实现步骤1、启动Hive Metastore服务2、启动Hive客户端3、创建Hive表,加载HDFS数据文件…...

Linux:不同计算机使用NFS共享资源
一,安装NFS文件系统 NFS即网络文件系统(network file system),它允许网络中的计算机之间通过网络共享资源。目前,NFS只用于在Linux和UNIX主机间共享文件系统。 #使用mount命令可以将远程主机的文件系统 安装到 本地: #将远程主机…...
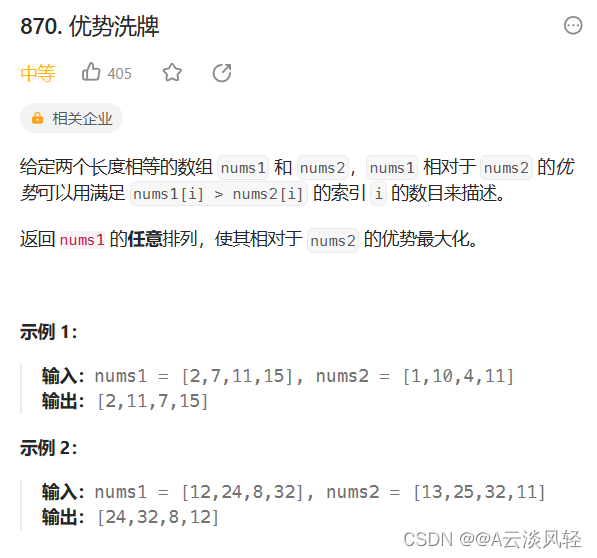
leetcode贪心算法题总结(一)
此系列分三章来记录leetcode的有关贪心算法题解,题目我都会给出具体实现代码,如果看不懂的可以后台私信我。 本章目录 1.柠檬水找零2.将数组和减半的最少操作次数3.最大数4.摆动序列5.最长递增子序列6.递增的三元子序列7.最长连续递增序列8.买卖股票的最…...

SQL高级:窗口函数
窗口函数,顾名思义,它的操作对象是窗口,即一个小的数据范围,而不是整个结果集。并且它是一个函数,在SQL中使用,所以一定有返回值。 窗口函数是SQL中非常有趣的部分,这一节我们就来学习一下它。 辅助表 方便我们后边的讲解,这里我们要建一张学生成绩表,建表语句如下…...
)
Excel formulas 使用总结(更新中)
最近在写task assigment的时候学习到的,记录下。 首先它所有需要写赋值formuls都要用 开头 相等赋值 a1 这个就代表这格的数据和a1是一样的。如果希望其他格和它相同的逻辑,可以直接复制该cell或者直接拖动该cell右下角,他会自动进行匹配…...

华为OD机试 - 两个字符串间的最短路径问题(Java JS Python C)
题目描述 给定两个字符串,分别为字符串 A 与字符串 B。 例如 A字符串为 "ABCABBA",B字符串为 "CBABAC" 可以得到下图 m * n 的二维数组,定义原点为(0,0),终点为(m,n),水平与垂直的每一条边距离为1,映射成坐标系如下图。 从原点 (0,0) 到 (0,A) 为水…...

强敌环伺:金融业信息安全威胁分析——钓鱼和恶意软件
门口的敌人:分析对金融服务的攻击 Akamai会定期针对不同行业发布互联网状态报告(SOTI),介绍相关领域最新的安全趋势和见解。最新的第8卷第3期报告主要以金融服务业为主,分析了该行业所面临的威胁和Akamai的见解。我们发…...

1月1日起,贵阳市退役军人可以免费乘坐公交地铁
广大退役军人是党和国家的宝贵财富,是新时代中国特色社会主义现代化建设的重要力量。为切实增强退役军人的幸福感与获得感,贵阳市信捷科技有限公司以“心系老兵情怀,热忱服务人民”为服务宗旨,积极响应贵阳市政府号召,…...

网络隔离后,怎样建立高效安全的数据安全交换通道?
数据安全对企业生存发展有着举足轻重的影响,数据资产的外泄、破坏都会导致企业无可挽回的经济损失和核心竞争力缺失。数据流动才能让其释放价值,想要保护企业核心资产,就要实现数据安全交换。 很多企业为了防止知识产权、商业机密数据泄露&am…...

Python:PyTorch
简介 PyTorch是一个开源的机器学习库,由Facebook的人工智能研究团队(FAIR)开发,用于应用于机器学习和深度学习的Python程序。PyTorch基于Torch,使用Python语言重新编写,使得它更容易使用和扩展。它支持强大…...
CentOS 5/6/7 基于开源项目制作openssh 9.6p1 rpm包—— 筑梦之路
背景介绍 开源项目地址:https://github.com/boypt/openssh-rpms.git 该项目主要支持了centos 5 、6、7版本,针对使用了比较老的操作系统进行openssh安全加固,还是不错的项目,使用简单、一件制作,欢迎大家去支持作者。…...

python的pandas数据分析处理基础学习
pandas学习 一、 pandas基础 1. 什么是pandas? 一个开源的python类库:用于数据分析、数据处理、数据可视化 高性能容易使用的数据结构容易使用的数据分析工具 很方便和其他类库一起使用: numpy:用于数学计算 scikit-learn&a…...

【Qt-容器类】
Qt编程指南 ■ 顺序容器类■ QList■ QVector■ QLinkedList■ QStack■ QQueue ■ 关联容器类■ QSet■ QMap■ QMultiMap■ QHash■ QMultiHash ■ 顺序容器类 ■ QList QList 比较常用的容器类,以数组列表的形式实现,在前、后添加数据非常快。以下为…...

2023-12-27 语音转文字的whisper应用部署
点击 <C 语言编程核心突破> 快速C语言入门 语音转文字的whisper应用部署 前言一、部署whisper二、部署whisper.cpp总结 前言 要解决问题: 需要一款开源的语音转文字应用, 用于视频自动转换字幕. 想到的思路: openai的whisper以及根据这个模型开发的whisper.cppC应用. …...
MAVLINK生成自定义消息
git clone https://github.com/mavlink/mavlink.gitcd mavlinkgit submodule update --init --recursivepython -m mavgenerate出现以下界面 XML填写自定义xml路径,内容可以参考mavlink/message_definitions/v1.0 Out为输出路径 <?xml version"1.0"…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...

Oracle11g安装包
Oracle 11g安装包 适用于windows系统,64位 下载路径 oracle 11g 安装包...

LCTF液晶可调谐滤波器在多光谱相机捕捉无人机目标检测中的作用
中达瑞和自2005年成立以来,一直在光谱成像领域深度钻研和发展,始终致力于研发高性能、高可靠性的光谱成像相机,为科研院校提供更优的产品和服务。在《低空背景下无人机目标的光谱特征研究及目标检测应用》这篇论文中提到中达瑞和 LCTF 作为多…...
