当前位置： 首页 > news >正文

Observer观察者模式（组件协作）

news 2026/2/10 8:41:44

观察者模式（组件协作）

链接：观察者模式实例代码 + 解析

目的

  • 在软件构建过程中，我们需要为某些对象建立一种“通知依赖关系” ——一个对象（目标对象）的状态发生改变，所有的依赖对象（观察者对象）都将得到通知。如果这样的依赖关系过于紧密，将使软件不能很好地抵御变化。

  • 使用面向对象技术，可以将这种依赖关系弱化，并形成一种稳定的依赖关系。从而实现软件体系结构的松耦合。

Ps.
虽然根据设计模式的思想我们应该去找该子模块的抽象类（父类），在使用时再具体去实例化对应的所需的子类.但是由于该模块扮演的角色是通知，所以完全可以将其完全脱离出去，并用一个抽象的通知机制替代，
而不是采用组合其抽象类的强耦合的方法。

模式定义

定义对象间的一种一对多（变化）的依赖关系，以便当一个对象(Subject)的状态发生改变时，所有依赖于它的对象都得到通知并自动更新。 ——《 设计模式》 GoF

要点总结

使用面向对象的抽象，Observer模式使得我们可以独立地改变目标与观察者，从而使二者之间的依赖关系达致松耦合。

  • 目标发送通知时，无需指定观察者，通知（可以携带通知信息作为参数）会自动传播。

  • 观察者自己决定是否需要订阅通知，目标对象对此一无所知。

  • Observer模式是基于事件的UI框架中非常常用的设计模式，也是MVC模式的一个重要组成部分。

    Eg.
    在这里插入图片描述

相关文章：

Observer观察者模式（组件协作）

观察者模式（组件协作） 链接：观察者模式实例代码 解析 目的 在软件构建过程中，我们需要为某些对象建立一种“通知依赖关系” ——一个对象（目标对象）的状态发生改变，所有的依赖对象&#xff0…...

编程日记 2023/12/31 5:47:00

数据挖掘 聚类度量

格式化之前的代码： import numpy as np#计算 import pandas as pd#处理结构化表格 import matplotlib.pyplot as plt#绘制图表和可视化数据的函数，通常与numpy和pandas一起使用。 from sklearn import metrics#聚类算法的评估指标。 from sklearn.clust…...

编程日记 2023/12/31 5:42:56

[Angular] 笔记 24：ngContainer vs. ngTemplate vs. ngContent

请说明 Angular 中 ngContainer， ngTemplate 和 ngContent 这三者之间的区别。 chatgpt 回答： 这三个在 Angular 中的概念是关于处理和组织视图的。 1. ngContainer： ngContainer 是一个虚拟的 HTML 容器，它本身不会在最终渲染…...

编程日记 2023/12/31 5:41:56

❀My排序算法学习之插入排序❀

目录 插入排序（Insertion Sort）:) 一、定义 二、基本思想 三、示例 时间复杂度 空间复杂度 bash C++ 四、稳定性分析...

编程日记 2023/12/31 5:40:55

【算法题】30. 串联所有单词的子串

题目 给定一个字符串 s 和一个字符串数组 words。 words 中所有字符串 长度相同。 s 中的 串联子串 是指一个包含 words 中所有字符串以任意顺序排列连接起来的子串。 例如，如果 words ["ab","cd","ef"]， 那么 "…...

编程日记 2023/12/31 5:39:53

SAP-FI模块 处理自动生成会计凭证增强

ENHANCEMENT 2 ZEHENC_SAPMF05A. "active version * FI 20221215：固定资产业务过渡科目摘要增强功能 WAIT UP TO 1 SECONDS.READ TABLE xbseg WITH KEY hkont 1601990001. IF sy-subrc 0.DATA: lt_bkdf TYPE TABLE OF bkdf,lt_bkpf TYPE TABLE OF bkpf,…...

编程日记 2023/12/31 5:36:51

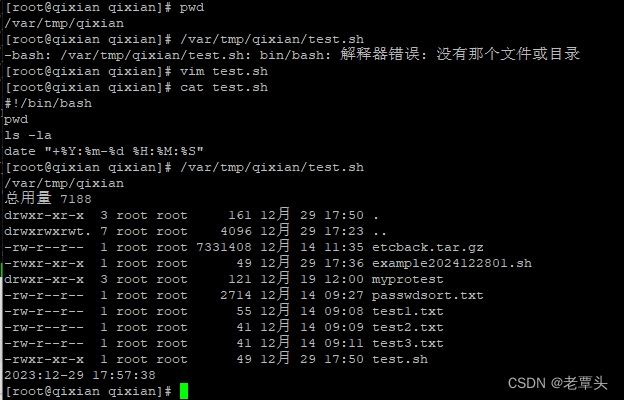
Shell脚本-bin/bash: 解释器错误: 没有那个文件或目录-完整路径执行-“/”引发的脑裂

引起该不适的一种可能以及解决方案，网上较多，比如： 但按以上方式操作，并经过查看，发现仍然未能解决问题。 因为两种方式执行，有一种能成功，有一种不能，刚开始未怀疑是文件问题&…...

编程日记 2023/12/31 5:33:48

React MUI（版本v5.15.2）详细使用

使用React MUI（版本v5.15.2）的详细示例。请注意，由于版本可能会有所不同，因此建议您查阅官方文档以获取最新的信息和示例。但是，我将根据我的知识库为您提供一些基本示例。 首先，确保您已经按照之前的说明…...

编程日记 2023/12/31 5:32:47

用CSS中的动画效果做一个转动的表

<!DOCTYPE html> <html lang"en"><head><meta charset"utf-8"><title></title><style>*{margin:0;padding:0;} /*制作表的样式*/.clock{width: 500px;height: 500px;margin:0 auto;margin-top:100px;border-rad…...

编程日记 2023/12/31 5:30:46

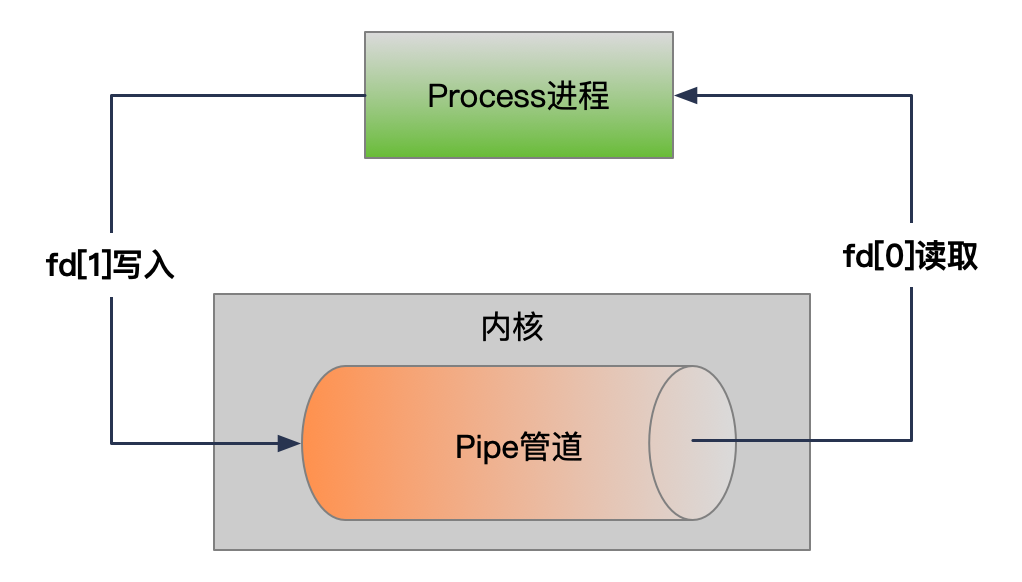
【linux】Linux管道的原理与使用场景

Linux管道是Linux命令行界面中一种强大的工具&#xff0c;它允许用户将多个命令链接起来&#xff0c;使得一个命令的输出可以作为另一个命令的输入。这种机制使得我们可以创建复杂的命令链&#xff0c;并在处理数据时提供了极大的灵活性。在本文中&#xff0c;我们将详细介绍Li…...

编程日记 2023/12/31 5:29:45

nvidia jetson xavier nx developer kit version emmc版重装系统

一、将开发板上的外置硬盘取下来格式化 二、在双系统ubuntu安装SDK Manager&#xff08;.deb文件&#xff09; SDK Manager | NVIDIA Developer sudo apt install ./sdkmanager_1.9.2-10884_amd64.deb 报错直接百度错误&#xff0c;执行相应命令即可 三、 运行SDK Manager …...

编程日记 2023/12/31 5:25:42

命令模式-实例使用

未使用命令模式的UML 使用命令模式后的UML public abstract class Command {public abstract void execute(); }public class Invoker {private Command command;/*** 为功能键注入命令* param command*/public void setCommand(Command command) {this.command command;}/***…...

编程日记 2023/12/31 5:23:40

将网页变身移动应用：网址封装成App的完全指南

什么是网址封装&#xff1f; 网址封装是一个将你的网站或网页直接嵌入到一个原生应用容器中的过程。用户可以通过下载你的App来访问网站&#xff0c;而无需通过浏览器。这种方式不仅提升了用户体验&#xff0c;还可利用移动设备的功能&#xff0c;如推送通知和硬件集成。 小猪…...

编程日记 2023/12/31 5:19:37

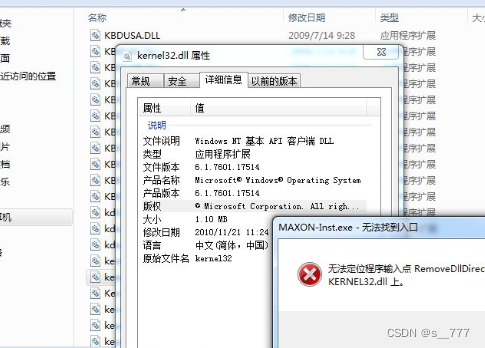
探讨kernel32.dll文件是什么，有效解决kernel32.dll丢失

在使用电脑时&#xff0c;你是否遇到过kernel32.dll丢失的困扰&#xff1f;面对这个问题&#xff0c;我们需要及时去解决kernel32.dll丢失的问题。接下来&#xff0c;我们将深入探讨kernel32.dll的功能以及其在操作系统和应用程序中的具体应用领域&#xff0c;相信这将对你解决…...

编程日记 2023/12/31 5:17:35

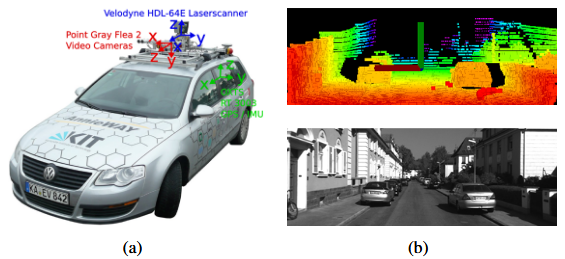
LOAM: Lidar Odometry and Mapping in Real-time 论文阅读

论文链接 LOAM: Lidar Odometry and Mapping in Real-time 0. Abstract 提出了一种使用二维激光雷达在6自由度运动中的距离测量进行即时测距和建图的方法 距离测量是在不同的时间接收到的&#xff0c;并且运动估计中的误差可能导致生成的点云的错误配准 本文的方法在不需要高…...

编程日记 2023/12/31 5:16:34

如何使用Docker将.Net6项目部署到Linux服务器（三）

目录 四 安装nginx 4.1 官网下载nginx 4.2 下载解压安装nginx 4.3 进行configure 4.4 执行make 4.5 查看nginx是否安装成功 4.6 nginx的一些常用命令 4.6.1 启动nginx 4.6.2 通过命令查看nginx是否启动成功 4.6.3 关闭Nginx 4.6.5 重启Nginx 4.6.6 杀掉所有Nginx进程 4.…...

编程日记 2023/12/31 5:10:29

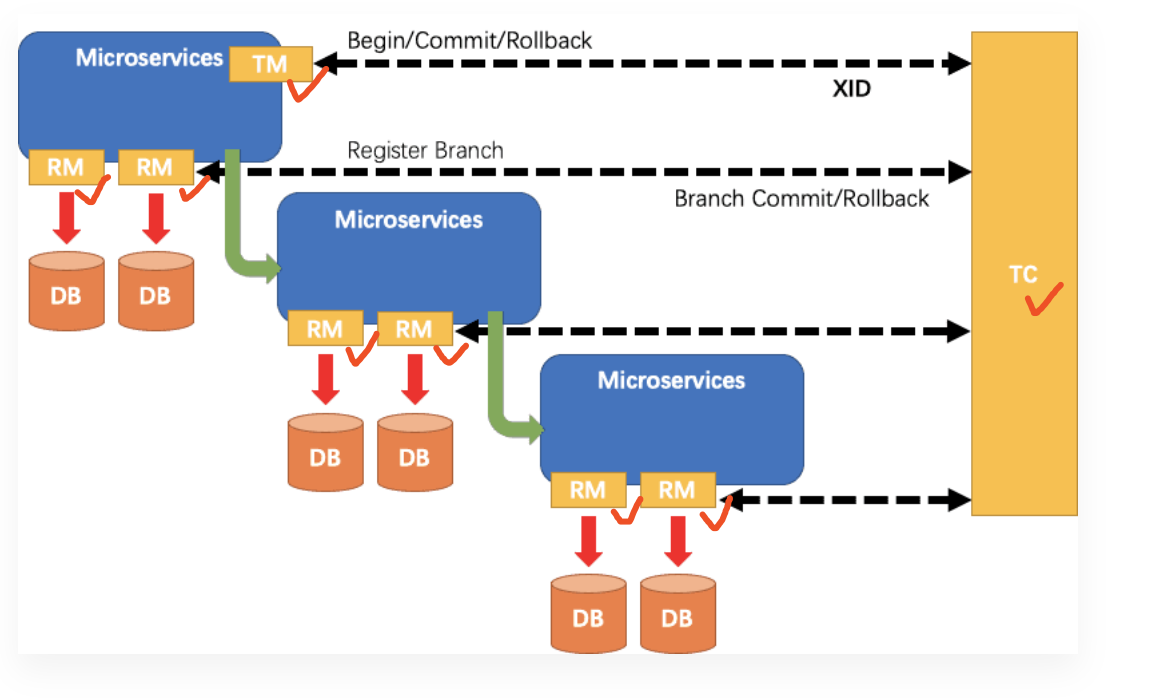
《Spring Cloud学习笔记：分布式事务Seata》

解决分布式事务的方案有很多&#xff0c;但实现起来都比较复杂&#xff0c;因此我们一般会使用开源的框架来解决分布式事务问题。 在众多的开源分布式事务框架中&#xff0c;功能最完善、使用最多的就是阿里巴巴在2019年开源的Seata了。 1. 初识Seata Seata是 2019 年 1 月…...

编程日记 2023/12/31 5:09:27

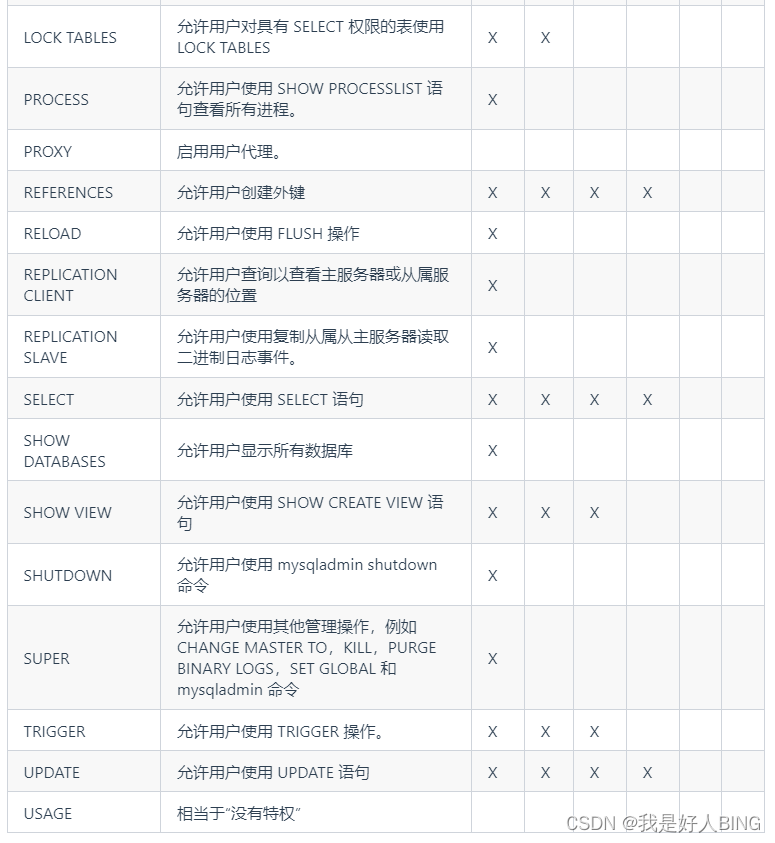
MySQL：权限控制

要授予用户帐户权限&#xff0c;可以用GRANT命令。有撤销用户的权限&#xff0c;可以用REVOKE命令。这里以 MySQl 为例&#xff0c;介绍权限控制实际应用。 GRANT授予权限语法&#xff1a; GRANT privilege,[privilege],.. ON privilege_level TO user [IDENTIFIED BY passwo…...

编程日记 2023/12/31 5:08:27

安全生产知识竞赛活动方案

为进一步普及安全生产法律法规知识&#xff0c;增强安全意识&#xff0c;提高安全技能&#xff0c;经研究&#xff0c;决定举办以“加强安全法治、保障安全生产”为主题的新修订《安全生产法》知识竞赛活动&#xff0c;现将有关事项通知如下&#xff1a; 一、活动时间&#xf…...

编程日记 2023/12/31 5:07:26

2023 IoTDB Summit：天谋科技 CTO 乔嘉林《IoTDB 企业版 V1.3： 时序数据管理一站式解决方案》...

12 月 3 日&#xff0c;2023 IoTDB 用户大会在北京成功举行&#xff0c;收获强烈反响。本次峰会汇集了超 20 位大咖嘉宾带来工业互联网行业、技术、应用方向的精彩议题&#xff0c;多位学术泰斗、企业代表、开发者&#xff0c;深度分享了工业物联网时序数据库 IoTDB 的技术创新…...

编程日记 2023/12/31 5:00:19

DockerHub与私有镜像仓库在容器化中的应用与管理

哈喽&#xff0c;大家好&#xff0c;我是左手python&#xff01; Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库&#xff0c;用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

编程新知 2025/10/8 10:56:25

反射获取方法和属性

Java反射获取方法 在Java中&#xff0c;反射&#xff08;Reflection&#xff09;是一种强大的机制&#xff0c;允许程序在运行时访问和操作类的内部属性和方法。通过反射&#xff0c;可以动态地创建对象、调用方法、改变属性值&#xff0c;这在很多Java框架中如Spring和Hiberna…...

编程新知 2025/11/9 2:57:17

是否存在路径（FIFOBB算法）

题目描述 一个具有 n 个顶点e条边的无向图&#xff0c;该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序&#xff0c;确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数&#xff0c;分别表示n 和 e 的值&#xff08;1…...

编程新知 2025/10/1 6:09:21

【无标题】路径问题的革命性重构：基于二维拓扑收缩色动力学模型的零点隧穿理论

路径问题的革命性重构&#xff1a;基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中&#xff08;图1&#xff09;&#xff1a; mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

编程新知 2025/10/21 1:07:59

Linux nano命令的基本使用

参考资料 GNU nanoを使いこなすnano基础 目录 一. 简介二. 文件打开2.1 普通方式打开文件2.2 只读方式打开文件 三. 文件查看3.1 打开文件时&#xff0c;显示行号3.2 翻页查看 四. 文件编辑4.1 Ctrl K 复制 和 Ctrl U 粘贴4.2 Alt/Esc U 撤回 五. 文件保存与退出5.1 Ctrl …...

编程新知 2026/1/31 2:17:41

恶补电源：1.电桥

一、元器件的选择 搜索并选择电桥&#xff0c;再multisim中选择FWB&#xff0c;就有各种型号的电桥: 电桥是用来干嘛的呢&#xff1f; 它是一个由四个二极管搭成的“桥梁”形状的电路&#xff0c;用来把交流电&#xff08;AC&#xff09;变成直流电&#xff08;DC&#xff09;。…...

编程新知 2026/2/9 5:44:35

算术操作符与类型转换：从基础到精通

目录 前言&#xff1a;从基础到实践——探索运算符与类型转换的奥秘 算术操作符超级详解 算术操作符&#xff1a;、-、*、/、% 赋值操作符&#xff1a;和复合赋值 单⽬操作符&#xff1a;、--、、- 前言&#xff1a;从基础到实践——探索运算符与类型转换的奥秘 在先前的文…...

编程新知 2026/2/5 4:00:38

WEB3全栈开发——面试专业技能点P4数据库

一、mysql2 原生驱动及其连接机制 概念介绍 mysql2 是 Node.js 环境中广泛使用的 MySQL 客户端库&#xff0c;基于 mysql 库改进而来&#xff0c;具有更好的性能、Promise 支持、流式查询、二进制数据处理能力等。 主要特点&#xff1a; 支持 Promise / async-await&#xf…...

编程新知 2025/8/17 13:47:50

C++--string的模拟实现

一,引言 string的模拟实现是只对string对象中给的主要功能经行模拟实现&#xff0c;其目的是加强对string的底层了解&#xff0c;以便于在以后的学习或者工作中更加熟练的使用string。本文中的代码仅供参考并不唯一。 二,默认成员函数 string主要有三个成员变量&#xff0c;…...

编程新知 2026/1/26 19:02:17

用 Rust 重写 Linux 内核模块实战：迈向安全内核的新篇章

用 Rust 重写 Linux 内核模块实战&#xff1a;迈向安全内核的新篇章 ​​摘要&#xff1a;​​ 操作系统内核的安全性、稳定性至关重要。传统 Linux 内核模块开发长期依赖于 C 语言&#xff0c;受限于 C 语言本身的内存安全和并发安全问题&#xff0c;开发复杂模块极易引入难以…...

编程新知 2025/10/25 19:31:21