力扣:509. 斐波那契数(动态规划,附带递归版本) 详细讲解动态规划的思路
题目:
斐波那契数 (通常用 F(n) 表示)形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是:
F(0) = 0,F(1) = 1
F(n) = F(n - 1) + F(n - 2),其中 n > 1
给定 n ,请计算 F(n) 。
示例 1:
输入:n = 2
输出:1
解释:F(2) = F(1) + F(0) = 1 + 0 = 1
示例 2:
输入:n = 3
输出:2
解释:F(3) = F(2) + F(1) = 1 + 1 = 2
示例 3:
输入:n = 4
输出:3
解释:F(4) = F(3) + F(2) = 2 + 1 = 3
提示:
0 <= n <= 30
思路:
本题很简单,但很适合用来做动态规划(和递归)的入门题,本篇文章主要讲解一下动态规划的思路。
动态规划
动规五部曲:
这里我们要用一个一维dp数组来保存递归的结果
- 确定dp数组以及下标的含义
dp[i]的定义为:第i个数的斐波那契数值是dp[i]
- 确定递推公式
为什么这是一道非常简单的入门题目呢?
因为题目已经把递推公式直接给我们了:状态转移方程 dp[i] = dp[i - 1] + dp[i - 2];
- dp数组如何初始化
题目中把如何初始化也直接给我们了,如下:
dp[0] = 0dp[1] = 1
- 确定遍历顺序
从递归公式dp[i] = dp[i - 1] + dp[i - 2];中可以看出,dp[i]是依赖 dp[i - 1] 和 dp[i - 2],那么遍历的顺序一定是从前到后遍历的
- 举例推导dp数组
按照这个递推公式dp[i] = dp[i - 1] + dp[i - 2],我们来推导一下,当N为10的时候,dp数组应该是如下的数列:
0 1 1 2 3 5 8 13 21 34 55
如果代码写出来,发现结果不对,就把dp数组打印出来看看和我们推导的数列是不是一致的。
以上就是动态规划五部曲 这在之后将贯穿所有动态规划类的题目
完整代码和复杂度分析:
动态规划版本1(定义dp数组):
class Solution:def fib(self, n: int) -> int:# 排除 Corner Caseif n == 0:return 0# 创建 dp table dp = [0] * (n + 1)# 初始化 dp 数组dp[0] = 0dp[1] = 1# 遍历顺序: 由前向后。因为后面要用到前面的状态for i in range(2, n + 1):# 确定递归公式/状态转移公式dp[i] = dp[i - 1] + dp[i - 2]# 返回答案return dp[n]
- 时间复杂度:O(n)
- 空间复杂度:O(n)
动态规划版本2(不自定义dp数组,仅使用3个变量来维护dp数组):
class Solution:def fib(self, n: int) -> int:if n <= 1:return ndp = [0, 1]for i in range(2, n + 1):total = dp[0] + dp[1]dp[0] = dp[1]dp[1] = totalreturn dp[1]
- 时间复杂度:O(n)
- 空间复杂度:O(1)
递归版本:
class Solution:def fib(self, n: int) -> int:if n < 2:return nreturn self.fib(n - 1) + self.fib(n - 2)
- 时间复杂度:O(2^n)
- 空间复杂度:O(n)
相关文章:
 详细讲解动态规划的思路)
力扣:509. 斐波那契数(动态规划,附带递归版本) 详细讲解动态规划的思路
题目: 斐波那契数 (通常用 F(n) 表示)形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是: F(0) 0,F(1) 1 F(n) F(n - 1) F(n - 2),其中…...

Python3,压箱底的代码片段,提升工作效率稳稳的。
压箱底代码存活 1、引言2、代码实例2.1 操作存储服务2.1.1 Redis操作2.1.2 MongoDB操作2.1.3 MySQL操作 2.2 异步操作2.3 多线程 3、总结 1、引言 小屌丝:鱼哥,这年底了,得不得分享一点压箱底的东西啊 小鱼:… 压箱底的东西&…...

Flowable-升级为7.0.0.M2-第三节
目录 启动项目添加虚拟机参数启动成功 启动项目 添加虚拟机参数 java.base/java.langALL-UNNAMED --add-opens java.base/java.mathALL-UNNAMED --add-opens java.base/java.util.concurrentALL-UNNAMED --add-opens java.base/java.netALL-UNNAMED --add-opens java.base/ja…...

JavaWeb——前端之AjaxVue
6. 前后端交互 6.1 Ajax(原生的) 概念: Asynchronous JavaScript And XML(异步的JavaScript和XML) 作用: 数据交互:通过Ajax可以给服务器发送请求,并获取服务器响应的数据异步交…...
在 Android 手机上从SD 卡恢复数据的 6 个有效应用程序
如果您有 Android 设备,您可能会将个人和专业的重要文件保存在设备的 SD 卡上。这些文件包括照片、视频、文档和各种其他类型的文件。您绝对不想丢失这些文件,但当您的 SD 卡损坏时,数据丢失是不可避免的。 幸运的是,您不需要这样…...

uni-app/vue封装etc车牌照输入,获取键盘按键键值
先看下效果如下: 动态图如下 uniapp的keyup获取不到keyCode和compositionstart,compositionend,所以需要监听input节点的keyup事件, 思路以及代码如下: 1.将每一个字符用文本框输入,代码如下 <view …...

iostat获取IO延迟单位从ms调整us的方案
iostat命令统计的磁盘I/O延迟通常是以毫秒(ms)为单位,例如在输出中的await字段表示的是平均服务时间,包括等待时间和处理时间,这个值就是以毫秒为单位。 然而,要获取更精确到微秒级别(us&#x…...

K8s 源码剖析及debug实战之 Kube-Scheduler(四):预选算法详解
文章目录 0. 引言1. 回顾2. podFitsOnNode 为什么执行两次预选3. 预选算法有哪些4. 参考 0. 引言 欢迎关注本专栏,本专栏主要从 K8s 源码出发,深入理解 K8s 一些组件底层的代码逻辑,同时借助 debug Minikube 来进一步了解 K8s 底层的代码运行…...
ES6之解构赋值详解
✨ 专栏介绍 在现代Web开发中,JavaScript已经成为了不可或缺的一部分。它不仅可以为网页增加交互性和动态性,还可以在后端开发中使用Node.js构建高效的服务器端应用程序。作为一种灵活且易学的脚本语言,JavaScript具有广泛的应用场景&#x…...
UntiyShader(五)属性、内置文件和变量
目录 一、如何使用属性 例子 ShaderLab中的属性的类型和Cg中的变量的类型之间的匹配关系 二、Unity提供的内置文件和变量 内置的包含文件 内置的变量 一、如何使用属性 在一开始我们提到过,材质和UnityShader之间有着密切的练习,我们可以通过材质面…...

Pytorch简介
1.1 Pytorch的历史 PyTorch是一个由Facebook的人工智能研究团队开发的开源深度学习框架。在2016年发布后,PyTorch很快就因其易用性、灵活性和强大的功能而在科研社区中广受欢迎。下面我们将详细介绍PyTorch的发展历程。 在2016年,Facebook的AI研究团队…...
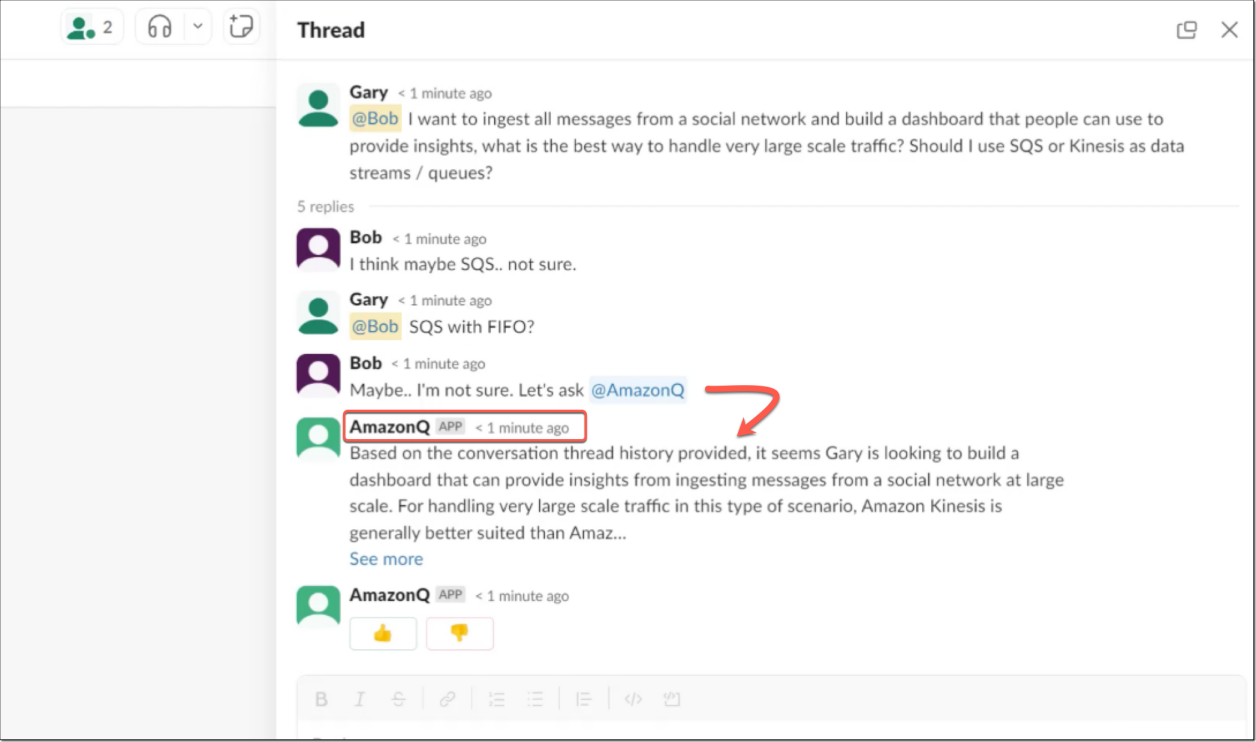
亚马逊云科技Amazon Q,一款基于生成式人工智能的新型助手
近日,亚马逊云科技宣布推出Amazon Q,这是一款基于生成式人工智能(AI)的新型助手,专为辅助工作而设计,可以根据您的业务量身定制。通过连接到公司的信息存储库、代码、数据和企业系统,可以使用Am…...
骑砍战团MOD开发(29)-module_scenes.py游戏场景
骑砍1战团mod开发-场景制作方法_哔哩哔哩_bilibilihttps://www.bilibili.com/video/BV1Cw411N7G4/ 一.骑砍游戏场景 骑砍战团中进入城堡,乡村,战斗地图都被定义为场景,由module_scenes.py进行管理。 scene(游戏场景) 天空盒(Skyboxes.py) 地形(terrain code) 场景物(scene_…...
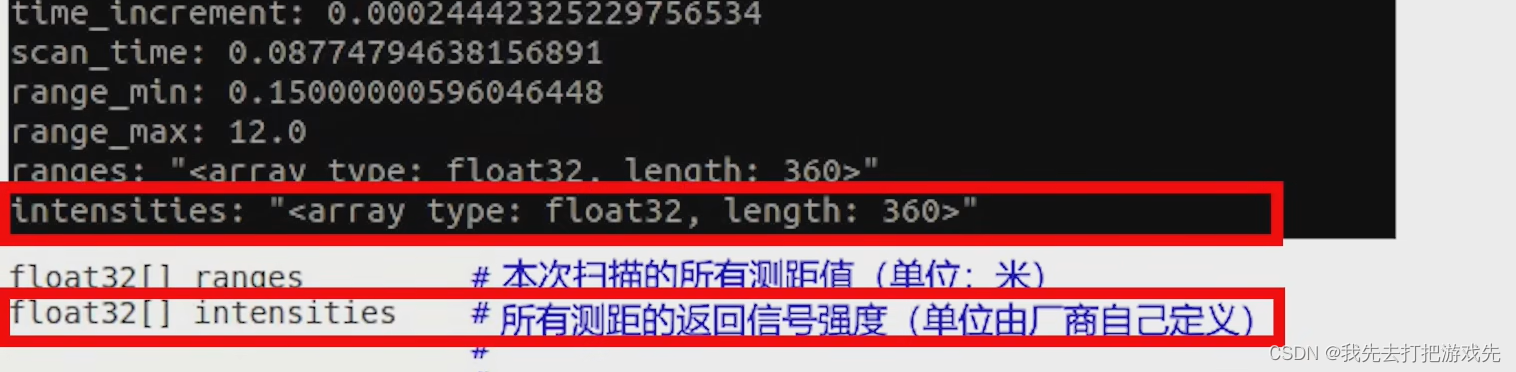
ROS学习记录:ROS系统中的激光雷达消息包的数据格式
一、在工作空间中输入source ./devel/setup.bash 二、输入roslaunch wpr_simulation wpb_simple.launch打开机器人仿真环境 三、机器人仿真环境打开成功 四、给机器人围上一圈障碍物 五、再打开一个工作空间终端 六、输入roslaunch wpr_simulation wpb_rviz.launch打开RViz 七、…...
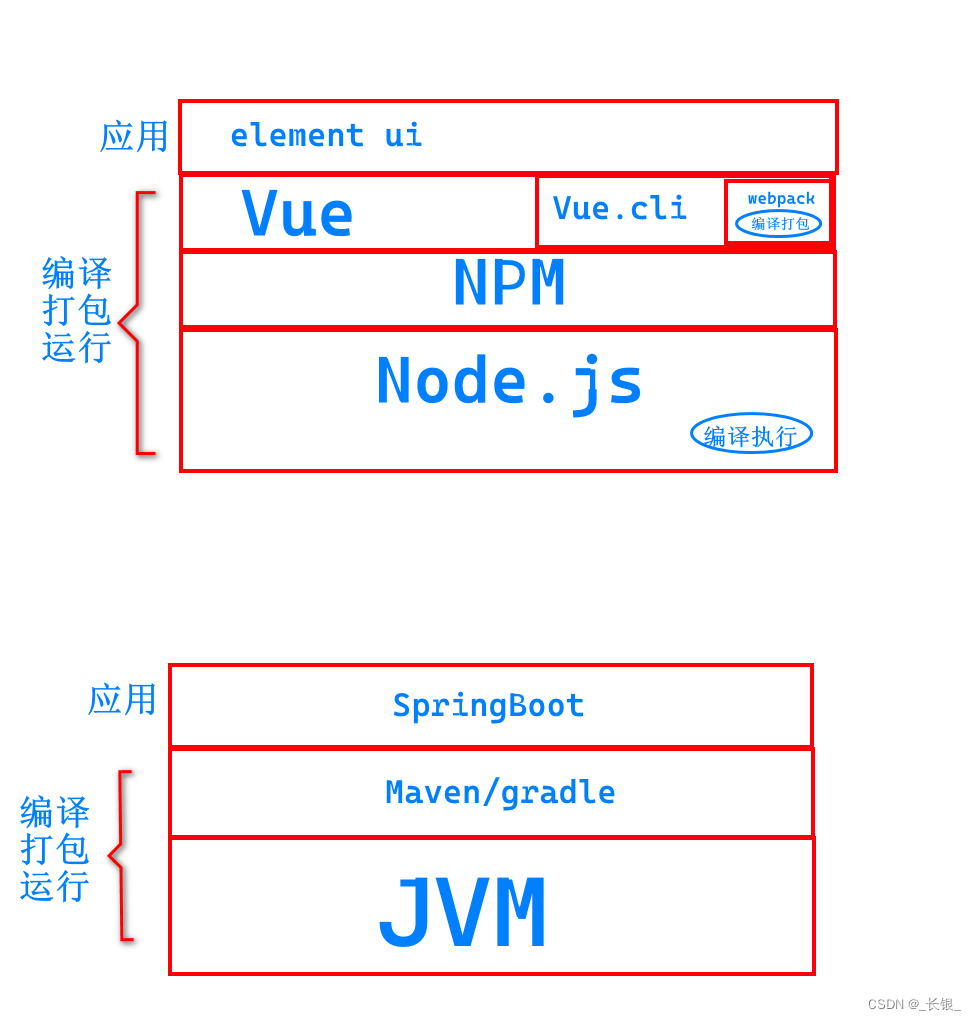
Vue.js和Node.js的关系--类比Java系列
首先我们看一张图 这里我们类比了Java的jvm和JavaScript的node.js。 可以看到,node.js是基础,提供了基础的编译执行的能力。vue,js是实际上定义了一种他自己的代码格式,以加速开发。...

我的笔记本电脑死机问题折腾记录
两年前,买了一台笔记本电脑。直到今年4月份,不到两年的时间,便出现了花屏的情况,然后就到官方售后去维修,换屏。然后在6月份,屏幕问题再次出现,又去售后维修。 经过两次维修,笔记本…...

uniApp中uView组件库的丰富布局方法
目录 基本使用 #分栏间隔 #混合布局 #分栏偏移 #对齐方式 API #Row Props #Col Props #Row Events #Col Events UniApp的uView组件库是一个丰富的UI组件库,提供了各种常用的UI组件和布局方法,帮助开发者快速构建美观、灵活的界面。下面给你写一…...
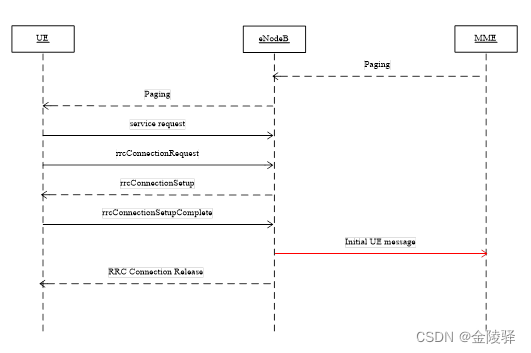
TDD-LTE 寻呼流程
目录 1. 寻呼成功流程 1.1 空闲态寻呼 1.2 连接态寻呼 2. 寻呼失败流程 2.1 Paging消息不可达 2.2 RRC建立失败 2.3 eNodeB未上发Initial UE message或达到超时 1. 寻呼成功流程 1.1 空闲态寻呼 寻呼成功:MME发起寻呼(S1 接口发送Paing 消息&…...
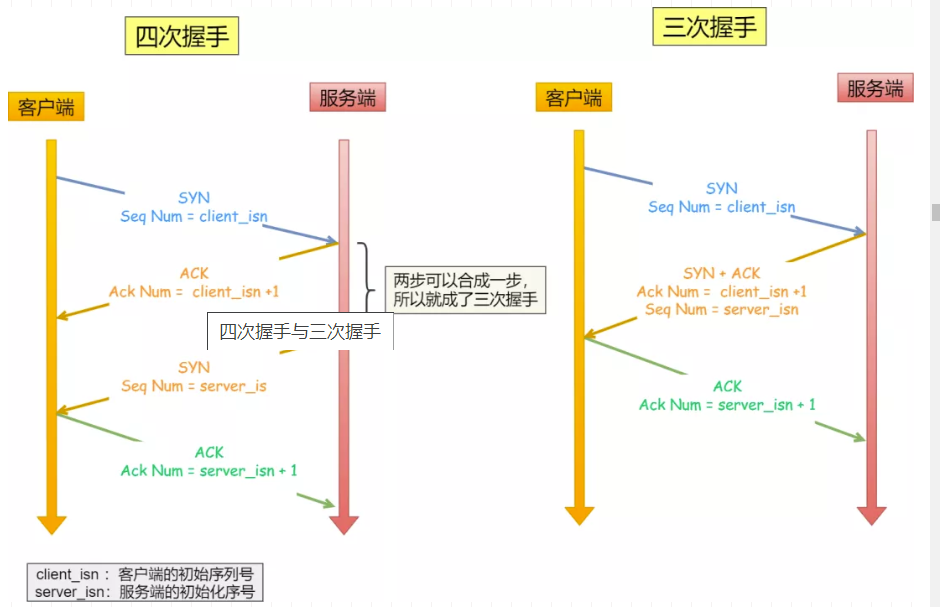
TCP中的三次握手和四次挥手
TCP中的连接和断开可以说是在面试中经常被问到的问题之一,正好有空就总结一下,首先回顾一下TCP的相关知识点 1. TCP的基础知识 1.1 TCP的基本概念 我们知道TCP是运输层的面向连接的可靠的传输协议。面向连接的,指的就是在两个进程发送数据…...
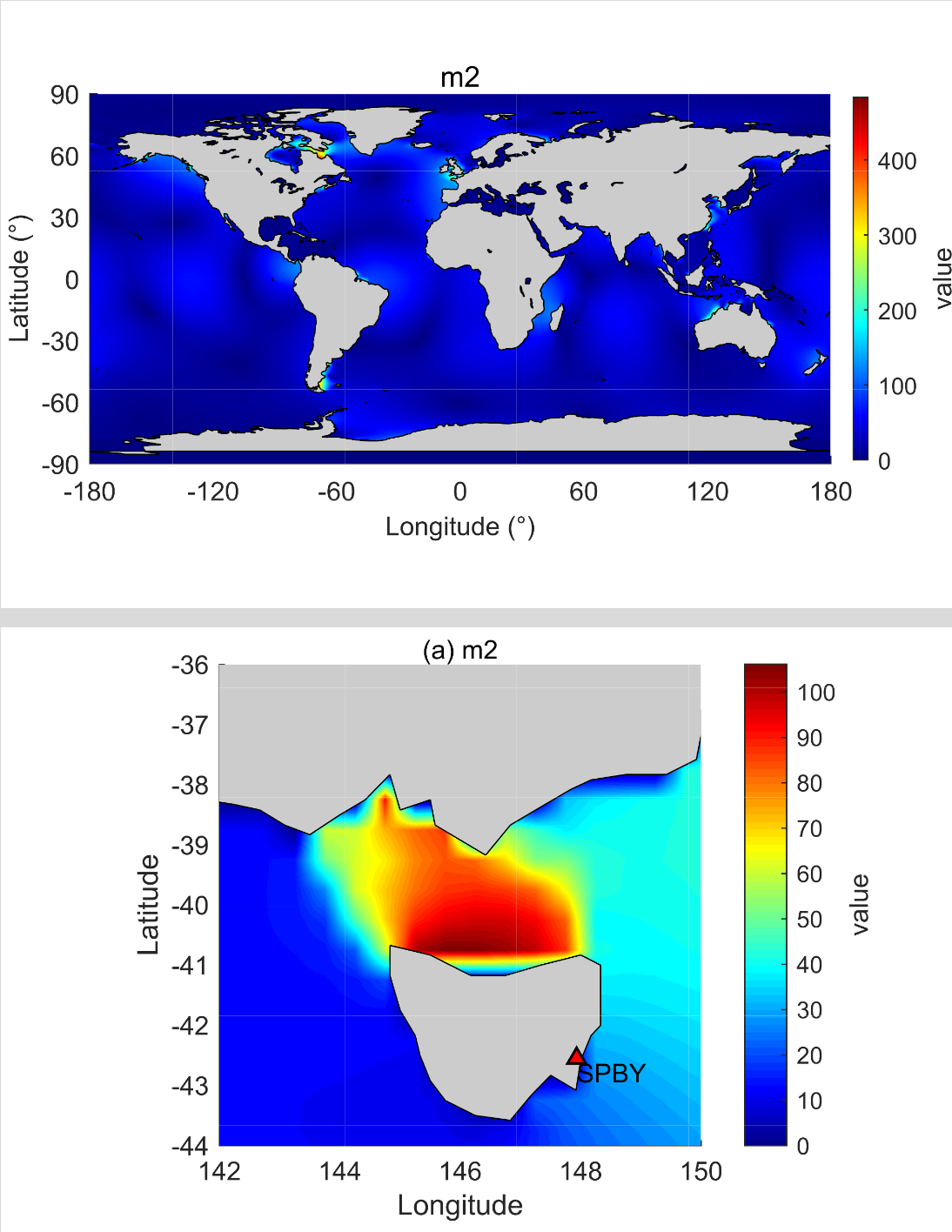
NAO.99b海潮模型的详解教程
NAO.99b模型是由日本国家天文台开发的全球潮汐模式,基于二维非线性浅水方程。该模型具有较高的分辨率,网格间距为0.50.5,网格数为720360,覆盖的经度范围为0.25~359.75E,纬度范围为89.75S~89.75N…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

Python 高效图像帧提取与视频编码:实战指南
Python 高效图像帧提取与视频编码:实战指南 在音视频处理领域,图像帧提取与视频编码是基础但极具挑战性的任务。Python 结合强大的第三方库(如 OpenCV、FFmpeg、PyAV),可以高效处理视频流,实现快速帧提取、压缩编码等关键功能。本文将深入介绍如何优化这些流程,提高处理…...

Spring AOP代理对象生成原理
代理对象生成的关键类是【AnnotationAwareAspectJAutoProxyCreator】,这个类继承了【BeanPostProcessor】是一个后置处理器 在bean对象生命周期中初始化时执行【org.springframework.beans.factory.config.BeanPostProcessor#postProcessAfterInitialization】方法时…...

Python的__call__ 方法
在 Python 中,__call__ 是一个特殊的魔术方法(magic method),它允许一个类的实例像函数一样被调用。当你在一个对象后面加上 () 并执行时(例如 obj()),Python 会自动调用该对象的 __call__ 方法…...
