当前位置：首页 > news >正文

Unity | Shader基础知识番外（向量数学知识速成）

news 2026/2/9 15:14:20

一、向量定义

二、计算向量

三、向量的加法（连续行走）

四、向量的长度

五、单位向量

六、向量的点积

1 计算

2 作用

七、向量的叉乘

1 承上启下

2 叉乘结论

3 叉乘的计算（这里看不懂就百度叉乘计算）

八、欢迎收看Shader专栏

一、向量定义

向量：从一个点到另一个点的箭头。

例：假如现在有两个点，A（0,0）和B点（4,5）。

假如从A走向B（如图1），箭头为：

假如从B走向A（如图2），箭头为：

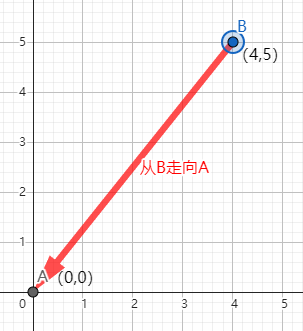
我们会用A（0,0）表示点A，

我们会用B（4,5）表示点B，

问题，我们用什么表示和区分这两个箭头？

答：如果从A走向B，我们就写成 $\vec{AB}$ ，如果从B走向A，就写成 $\vec{BA}$ （是不是很形象）。

字母确定了，可数字怎么办？

答：因为横坐标x是向左为正，纵坐标y是向上为正。

我们从A（0,0）走向B（4,5）等于向右走4格，向上走5格，所以是 $\vec{AB}$ （4，5），

反之，如果从B（4,5）走向A（0,0）等于向左走4格，向下走5格，所以是 $\vec{BA}$ （-4，-5），

所以在表达向量时，写的是箭头起点到箭头终点是如何走过去。

二、计算向量

（如图3）如果我们随意画出两个点A（1,3），B（4,5）

通过数格子，我们可以得出 $\vec{AB}$ （3，2），但这个数字，我们也可以算出来，通过终点的B（4,5）中的x减去A（1,3）的x：4-1=3，通过终点的B（4,5）中的y减去A（1,3）的y：5-3=2

也可以得出： $\vec{AB}$ （3，2）

所以：终点的坐标，减去起点的坐标，就是向量的数值

三、向量的加法（连续行走）

（如图4）我们画两个连着的向量 $\vec{AB}$ （1，3）和 $\vec{BC}$ （3，2）：

从图中（如图5）我们可以看出，我们从A走到B，又从B走到C，这种连着走的向量我们可以相加，实际上两个向量就是从A走到了C，横着向右走了4格，向上走了5格。

$\vec{AB}$ （1，3）+ $\vec{BC}$ （3，2）= $\vec{AC}$ （1+3，3+2）= $\vec{AC}$ （4，5）

四、向量的长度

（如图6）假如我希望计算 $\vec{AC}$ （4，5）的长度，通过我们学过的勾股定理就得出

AC = $\sqrt{4^{2}+5^{2}}$

所以：向量的长度为 $\sqrt{x^{2}+y^{2}}$

五、单位向量

单位向量：向量长度是1

把任何一个向量变成单位向量，只需要除以向量的长度。

例：向量（3,4），长度是5，希望长度变为1，就直接集体除以5。

所以，向量（3,4）的单位向量就是（3/5,4/5）。

六、向量的点积

1 计算

设向量a(1,2)和向量b（3,4）点乘

算法1：

$\vec{a}\cdot \vec{b}=(x_{1}\times x_{2})+(y_{1}\times y_{2})=(1\times 3)+(2\times 4)=3+8=11$

算法2：

$\vec{a}\cdot \vec{b}=|\vec{a}||\vec{b}|cos\theta=\sqrt{1^{2}+2^{2}}\sqrt{3^{2}+4^{2}}cos\theta$

算法2算到这一步就停了，因为不知道cosθ，

可是算法1和算法2的结果是相同的。

$\sqrt{1^{2}+2^{2}}\sqrt{3^{2}+4^{2}}cos\theta=11$

所以，可以算出 $cos\theta=\frac{11}{\sqrt{1^{2}+2^{2}}\sqrt{3^{2}+4^{2}}}=0.98$

最后θ≈11.5°

2 作用

为啥要算点积？（我们把上面的向量a和向量b画出来）（如图7）

我原本面向A（向量a）,现在我想面向B，我应该旋转多少度？

答：刚才算过了：11.5°

备注（以下结论的推导过程自己百度）：

$\vec{a}\cdot \vec{b}$ >0 a和b的夹角0-90度之间

$\vec{a}\cdot \vec{b}$ =0 a和b的夹角为90度

$\vec{a}\cdot \vec{b}$ <0 a和b的夹角大于90度

七、向量的叉乘

1 承上启下

第六部分我们知道了旋转角度，不知道聪明的你有没有发现，其实，你只知道了角度，不知道是顺时针旋转还是逆时针旋转。叉乘就事帮助我们判断是哪个方向的旋转的。

2 叉乘结论

当叉乘结果<0 顺时针旋转

当叉乘结果>0 逆时针旋转

叉乘结果=0 不用旋转

3 叉乘的计算（这里看不懂就百度叉乘计算）

我们还是计算向量a(1,2)和向量b（3,4）叉乘，因为叉乘需要x,y,z才能计算，此时相当于我们的z是0，所以我们的向量为a(1,2,0)和向量b（3,4,0）。

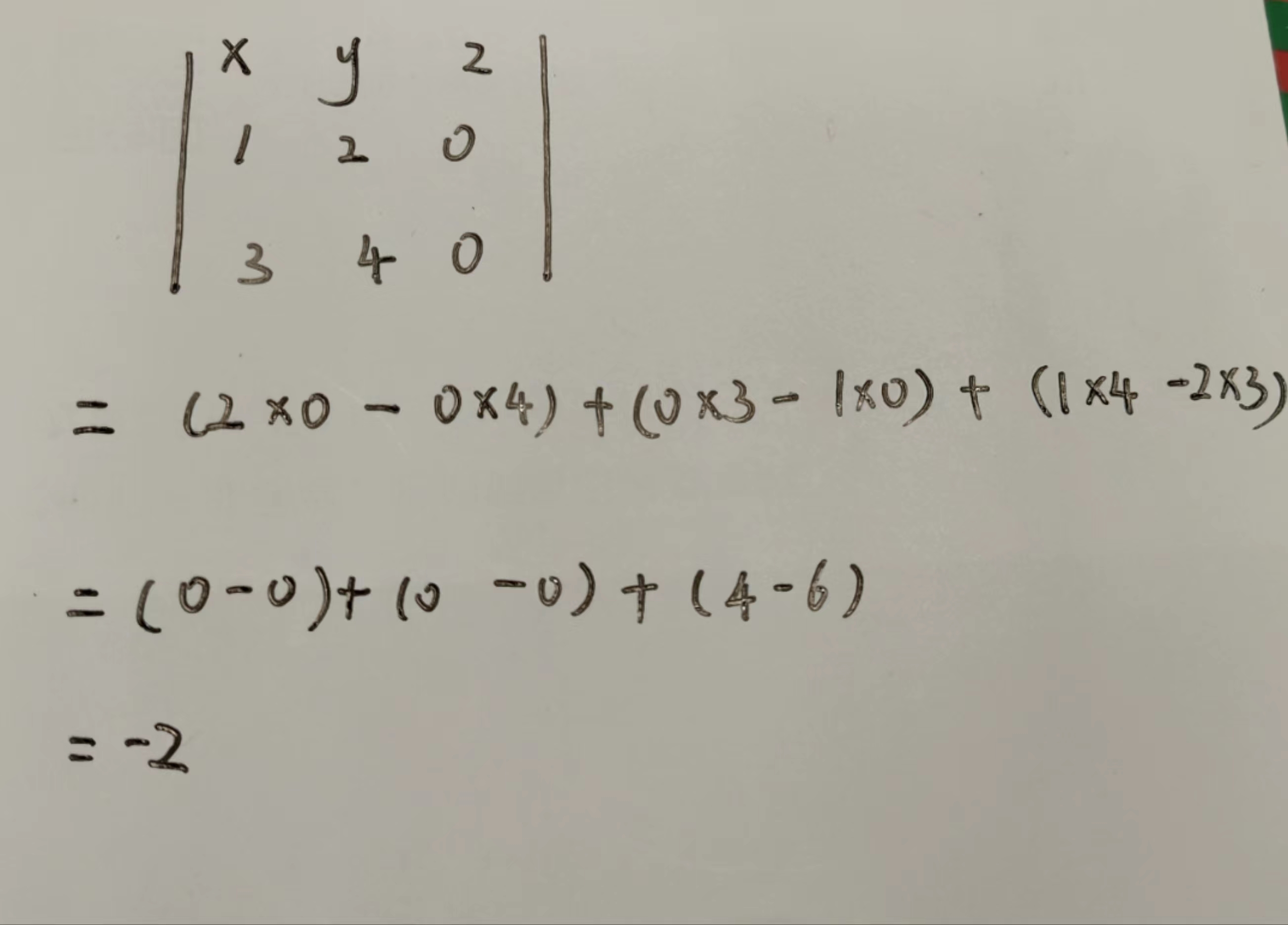
此时是-2<0所以，我们只需要逆时针旋转11.5°，就可以从向量a的方向变成向量b的方向。

八、欢迎收看Shader专栏

https://blog.csdn.net/weixin_49427945/category_12525804.html

Unity | Shader基础知识番外（向量数学知识速成）

目录一、向量定义二、计算向量三、向量的加法（连续行走） 四、向量的长度五、单位向量六、向量的点积 1 计算 2 作用七、向量的叉乘 1 承上启下 2 叉乘结论 3 叉乘的计算（这里看不懂就百度叉乘计算） 八、欢迎收…...

编程日记 2024/1/4 18:16:39

一个小白的微不足道的见解关于未来

随着科技的不断发展，IT行业日益壮大，运维工程师在其中扮演着至关重要的角色。他们负责维护和管理企业的技术基础设施，确保系统的正常运行。然而，随着技术的进步和行业的变化，运维工程师的未来将面临着一系列挑战和机遇…...

编程日记 2024/1/4 18:15:38

图的遍历（搜索）算法（深度优先算法DFS和广度优先算法BFS）

一、图的遍历的定义： 从图的某个顶点出发访问遍图中所有顶点，且每个顶点仅被访问一次。（连通图与非连通图） 二、深度优先遍历（DFS）； 1、访问指定的起始顶点； 2、若当前访问的顶点…...

编程日记 2024/1/4 18:14:36

抖店做不起来？新手常见起店失败问题总结，看下你中了几条？

我是王路飞。能看到这篇文章的，肯定是处境符合标题内容了。抖店的门槛很低，运营思路其实也不算难，但就是很多新手做不起来。这中间，可能跟平台、项目没什么关系，而是跟你自己有关系，走错了方向&#…...

编程日记 2024/1/4 18:13:36

【每日面试题】精选java面试题之redis

Redis是什么？为什么要使用Redis？ Redis是一个开源的高性能键值对存储数据库。它提供了多种数据结构，包括字符串、列表、集合、有序集合、哈希表等。Redis具有快速、可扩展、持久化、支持多种数据结构等特点，适用于缓存、消息队列…...

编程日记 2024/1/4 18:11:34

端口扫描 nmap nmap -O 192.168.162.172 smb枚举 smbmap(kali自带) //枚举GUEST用户可以使用的目录 smbmap -u GUEST -H 192.168.162.172 NTLMrelay—smbrelay 1.制作钓鱼文件使用GitHub - xct/hashgrab: generate payloads that force authentication against an attacker…...

编程日记 2024/1/4 18:09:31

uniapp子组件向父组件传值

目录子组件向父组件传值子组件1子组件2 父组件最后子组件向父组件传值子组件1 <template><view class"content"><view v-for"(item,index) in list" :key"index">{{item}}</view></view> </template>&…...

编程日记 2024/1/4 18:08:30

过滤特殊微信昵称

$nickName preg_replace(/[\xf0-\xf7].{3}/, , $userData[nickName]);...

编程日记 2024/1/4 18:06:28

LLM、AGI、多模态AI 篇一：开源大语言模型简记

文章目录系列开源大模型LlamaChinese-LLaMA-AlpacaLlama2-ChineseLinlyYaYiChatGLMtransformersGPT-3（未完全开源）BERTT5QwenBELLEMossBaichuan...

编程日记 2024/1/4 18:04:27

微信小程序中获取用户当前位置的解决方案

微信小程序中获取用户当前位置的解决方案 1 概述微信小程序有时需要获取用户当前位置，以便为用户提供基于位置信息的服务（附近美食、出行方案等）。获取用户当前位置的前提是用户手机需要打开 GPS 定位开关；其次，微…...

编程日记 2024/1/4 18:03:26

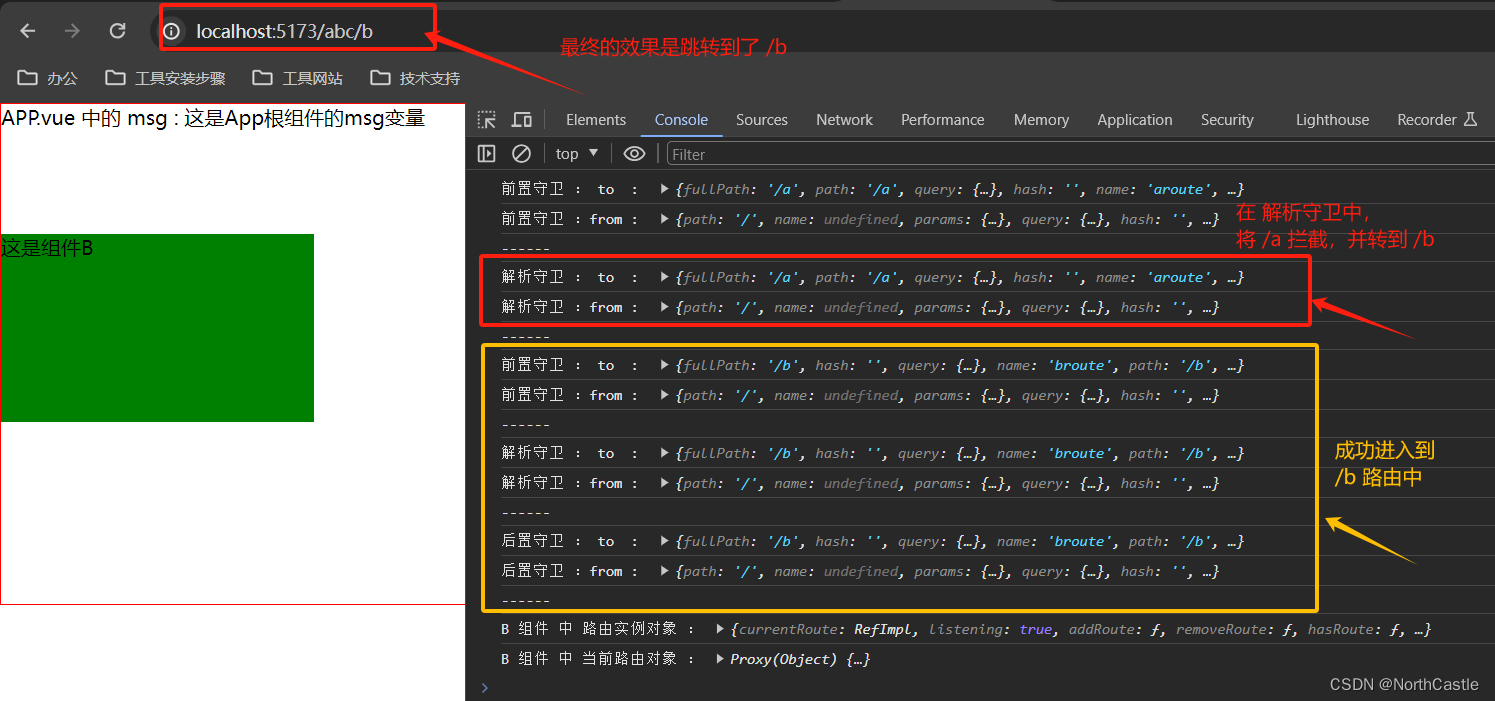
Vue3-35-路由-路由守卫的简单认识

什么是路由守卫路由守卫，就是在路由跳转的过程中， 可以进行一些拦截，做一些逻辑判断， 控制该路由是否可以正常跳转的函数。常用的路由守卫有三个 ： beforeEach() : 前置守卫，在路由跳转前就会被拦截&…...

编程日记 2024/1/4 18:02:25

制药企业符合CSV验证需要注意什么？

在制药行业中，计算机化系统验证（CSV）是确保生产过程的合规性和数据完整性的关键要素。通过CSV验证，制药企业可以保证其计算机化系统的可靠性和合规性，从而确保产品质量和患者安全。然而，符合CSV验证并不是一…...

编程日记 2024/1/4 18:00:23

再谈动态SQL

专栏精选引入Mybatis Mybatis的快速入门 Mybatis的增删改查扩展功能说明 mapper映射的参数和结果 Mybatis复杂类型的结果映射 Mybatis基于注解的结果映射 Mybatis枚举类型处理和类型处理器再谈动态SQL Mybatis配置入门 Mybatis行为配置之Ⅰ—缓存 Mybatis行为配置…...

编程日记 2024/1/4 17:58:21

【数据结构】树

一.二叉树的基本概念和性质： 1.二叉树的递归定义： 二叉树或为空树，或是由一个根结点加上两棵分别称为左子树和右子树的、互不相交的二叉树组成 2.二叉树的特点： （1）每个结点最多只有两棵子树&#xff0…...

编程日记 2024/1/4 17:57:21

【Midjourney】AI绘画新手教程（一）登录和创建服务器，生成第一幅画作

一、登录Discord 1、访问Discord官网使用柯學尚网（亲测非必须，可加快响应速度）访问Discord官方网址：https://discord.com 选择“在您的浏览器中打开Discord” 然后，注册帐号、购买套餐等，在此不做缀述。…...

编程日记 2024/1/4 17:56:20

对比 PyTorch 和 TensorFlow：选择适合你的深度学习框架

目录引言深度学习在各行业中的应用 PyTorch 和 TensorFlow 简介 PyTorch：简介与设计理念发展历史和背景主要特点和设计理念 TensorFlow：简介与设计理念发展历史和背景主要特点和设计理念 PyTorch 和 TensorFlow 的重要性 Pytorch对比Te…...

编程日记 2024/1/4 17:53:17

Oracle笔记-查看表已使用空间最大空间

目前以Oracle18c为例，主要是查这个表USER_SEGMENTS。在 Oracle 18c 数据库中，USER_SEGMENTS 是一个系统表，用于存储当前用户（当前会话）拥有的所有段的信息。段是 Oracle 中分配存储空间的逻辑单位，用于存…...

编程日记 2024/1/4 17:52:16

大数据HCIE成神之路之特征工程——特征选择

特征选择 1.1 特征选择 - Filter方法1.1.1 实验任务1.1.1.1 实验背景1.1.1.2 实验目标1.1.1.3 实验数据解析1.1.1.4 实验思路 1.1.2 实验操作步骤 1.2 特征选择 - Wrapper方法1.2.1 实验任务1.2.1.1 实验背景1.2.1.2 实验目标1.2.1.3 实验数据解析1.2.1.4 实验思路 1.2.2 实验操…...

编程日记 2024/1/4 17:51:15

python 正则-常见题目

1、邮箱 print(re.findall(r[\w-][\w-]\.[\w-], weidianqq.com))2、身份证号 xxxxxx yyyy MM dd 375 0 十八位 print(re.findall(r(?:18|19|(?:[23]\d))\d{2}, 2010)) # 年print(re.findall(r(?:0[1-9])|10|11|12, 11)) # 月print(re.findall(r(?:[0-2][1-9])|10|20|30|3…...

编程日记 2024/1/4 17:50:13

解析：Eureka的工作原理

Eureka是Netflix开源的一个基于REST的的服务发现注册框架，它遵循了REST协议，提供了一套简单的API来完成服务的注册和发现。Eureka能够帮助分布式系统中的服务提供者自动将自身注册到注册中心，同时也能够让服务消费者从注册中心发现服务提供者…...

编程日记 2024/1/4 17:46:09

Python｜GIF 解析与构建（5）：手搓截屏和帧率控制

目录 Python｜GIF 解析与构建（5）：手搓截屏和帧率控制一、引言二、技术实现：手搓截屏模块 2.1 核心原理 2.2 代码解析：ScreenshotData类 2.2.1 截图函数：capture_screen 三、技术实现&…...

编程新知 2025/11/14 3:06:30

多云管理“拦路虎”：深入解析网络互联、身份同步与成本可视化的技术复杂度

一、引言：多云环境的技术复杂性本质企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时，基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套：跨云网络构建数据…...

编程新知 2026/2/8 16:53:48

如何在看板中体现优先级变化

在看板中有效体现优先级变化的关键措施包括：采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中，设置任务排序规则尤其重要，因为它让看板视觉上直观地体…...

编程新知 2026/1/23 12:42:28

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

编程新知 2026/1/26 21:57:45

[10-3]软件I2C读写MPU6050 江协科技学习笔记（16个知识点）

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

编程新知 2026/1/28 8:34:48

Module Federation 和 Native Federation 的比较

前言 Module Federation 是 Webpack 5 引入的微前端架构方案，允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。概念解析 Module Federation (模块联邦) Modul…...

编程新知 2026/1/31 13:48:37

【无标题】路径问题的革命性重构：基于二维拓扑收缩色动力学模型的零点隧穿理论

路径问题的革命性重构：基于二维拓扑收缩色动力学模型的零点隧穿理论一、传统路径模型的根本缺陷在经典正方形路径问题中（图1）： mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

编程新知 2025/10/21 1:07:59