洛谷——P1347 排序(图论-拓扑排序)
文章目录
- 一、题目
- 排序
- 题目描述
- 输入格式
- 输出格式
- 样例 #1
- 样例输入 #1
- 样例输出 #1
- 样例 #2
- 样例输入 #2
- 样例输出 #2
- 样例 #3
- 样例输入 #3
- 样例输出 #3
- 提示
- 二、题解
- 基本思路:
- 代码
一、题目
排序
题目描述
一个不同的值的升序排序数列指的是一个从左到右元素依次增大的序列,例如,一个有序的数列 A , B , C , D A,B,C,D A,B,C,D 表示 A < B , B < C , C < D A<B,B<C,C<D A<B,B<C,C<D。在这道题中,我们将给你一系列形如 A < B A<B A<B 的关系,并要求你判断是否能够根据这些关系确定这个数列的顺序。
输入格式
第一行有两个正整数 n , m n,m n,m, n n n 表示需要排序的元素数量, 2 ≤ n ≤ 26 2\leq n\leq 26 2≤n≤26,第 1 1 1 到 n n n 个元素将用大写的 A , B , C , D , … A,B,C,D,\dots A,B,C,D,… 表示。 m m m 表示将给出的形如 A < B A<B A<B 的关系的数量。
接下来有 m m m 行,每行有 3 3 3 个字符,分别为一个大写字母,一个 < 符号,一个大写字母,表示两个元素之间的关系。
输出格式
若根据前 x x x 个关系即可确定这 n n n 个元素的顺序 yyy..y(如 ABC),输出
Sorted sequence determined after xxx relations: yyy...y.
若根据前 x x x 个关系即发现存在矛盾(如 A < B , B < C , C < A A<B,B<C,C<A A<B,B<C,C<A),输出
Inconsistency found after x relations.
若根据这 m m m 个关系无法确定这 n n n 个元素的顺序,输出
Sorted sequence cannot be determined.
(提示:确定 n n n 个元素的顺序后即可结束程序,可以不用考虑确定顺序之后出现矛盾的情况)
样例 #1
样例输入 #1
4 6
A<B
A<C
B<C
C<D
B<D
A<B
样例输出 #1
Sorted sequence determined after 4 relations: ABCD.
样例 #2
样例输入 #2
3 2
A<B
B<A
样例输出 #2
Inconsistency found after 2 relations.
样例 #3
样例输入 #3
26 1
A<Z
样例输出 #3
Sorted sequence cannot be determined.
提示
2 ≤ n ≤ 26 , 1 ≤ m ≤ 600 2 \leq n \leq 26,1 \leq m \leq 600 2≤n≤26,1≤m≤600。
二、题解
基本思路:
- 很明显这是一道拓扑排序的题,基本是是个模板题,考察的是对拓扑排序得理解。
- 输出结果有三种,再每次输入一对关系后进行拓扑排序判断
- 一:拓扑序列结果为n个元素且最长链也得是n
- 二:图中不能有环,有环即存在矛盾。而拓扑排序可以判断一个图中有没有环,当拓扑序列的长度不是已读入元素的个数时,说明有环。
- 三:在输入m个关系后,前俩个都不是,说明还没确定关系
代码
#include<bits/stdc++.h>
using namespace std;#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define endl "\n"
#define int long long
#define fi first
#define se second
#define repn(i,o,n) for(int i=o;i<=n;i++)
#define rep(i,o,n) for(int i=o;i<n;i++)
const int N = 30;
int n,m,d[N],rd[N];
vector<int> edge[N];
set<char> b;//存放当前读入的元素,用count函数来判断有没有读入
bool flag=false;//还没找到答案
//1.拓扑序列结果为n个元素且最长链也得是n
//2.图中不能有环,有环即存在矛盾
//3.在输入m个关系后,拓扑序列的结果!=n inline void TopoSort(int num){queue<pair<int,int>> q;//第一个参数存得是点,第二个是以该节点为结尾得链得长度 vector<int> ans;//存放拓扑序列 int maxn=0;//找最长链 repn(i,1,n)//入度为0的点且已经读入了该点的点入队 if(!rd[i]&&b.count((char)(i+'A'-1))) q.push({i,1});while(!q.empty()){auto x=q.front();q.pop();ans.push_back(x.fi);//拓扑序列每个节点出队一次 for(auto y:edge[x.fi])if(--rd[y]==0){q.push({y,x.se+1});maxn=max(maxn,x.se+1); //找到最长链 }}if(maxn==n){//最长链为n个元素说明已经确定了n个元素的顺序 cout<<"Sorted sequence determined after "<<num<<" ";cout<<"relations: ";rep(i,0,ans.size()){cout<<(char)(ans[i]+'A'-1);//输出拓扑序列 }cout<<'.'<<endl;//!!!注意还得输出个'.' flag=true; return ;}//cout<<ans.size()<<endl;if(ans.size()!=b.size()){cout<<"Inconsistency found after "; cout<<num<<" relations."<<endl;flag=true;return ;}
}void solve() {cin>>n>>m;repn(i,1,m) {string s;cin>>s;b.insert(s[0]),b.insert(s[2]);edge[s[0]-'A'+1].push_back(s[2]-'A'+1);++d[s[2]-'A'+1];repn(i,1,n)rd[i]=d[i];TopoSort(i);if(flag) return ;if(i==m){//i==m时,前两个都不是,说明还没确定关系 cout<<"Sorted sequence cannot be determined."<<endl;}}}signed main() {//IOS;int T=1;//cin>>T;while(T--) {solve();}return 0;
}相关文章:
)
洛谷——P1347 排序(图论-拓扑排序)
文章目录 一、题目排序题目描述输入格式输出格式样例 #1样例输入 #1样例输出 #1 样例 #2样例输入 #2样例输出 #2 样例 #3样例输入 #3样例输出 #3 提示 二、题解基本思路:代码 一、题目 排序 题目描述 一个不同的值的升序排序数列指的是一个从左到右元素依次增大的…...

JVM内存管理
一.java程序运行过程 JDK,JRE,JVM JVM把我们的字节码翻译成机械能执行的机械码。 JRE除了包含JVM之外,还包含很多java的原生依赖库。 JDK除了包含JRE之外,还包含很多工具,比如javac工具。 .java文件是怎么被执行的 我们的.java文件会被…...

将 Python 和 Rust 融合在一起,为 pyQuil® 4.0 带来和谐
文章目录 前言设定方向从 Rust 库构建 Python 软件包改装 pyQuil异步困境回报:功能和性能结论 前言 pyQuil 一直是在 Rigetti 量子处理单元(QPUs)上构建和运行量子程序的基石,通过我们的 Quantum Cloud Services(QCS™…...

Spring Boot应用程序中VO的理解及使用
在Spring Boot应用程序中,VO(View Object)通常用于表示视图层所需的数据,这些数据来自于业务逻辑层或数据访问层。VO的主要目的是将业务逻辑层的数据结构转换为视图层可以使用的数据结构,使得视图层可以直接使用VO中的…...
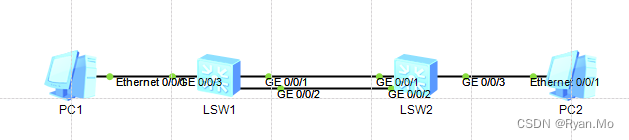
华为交换机ETH-TRUNK链路聚合lacp模式与手工模式
SW1配置如下 vlan batch 10interface Eth-Trunk1port link-type trunkport trunk allow-pass vlan 10mode lacp-static #手工模式删除改行max active-linknumber 2 #手工模式删除改行trunkport GigabitEthernet 0/0/1 to 0/0/2#配置为主设备(修改优先级&…...
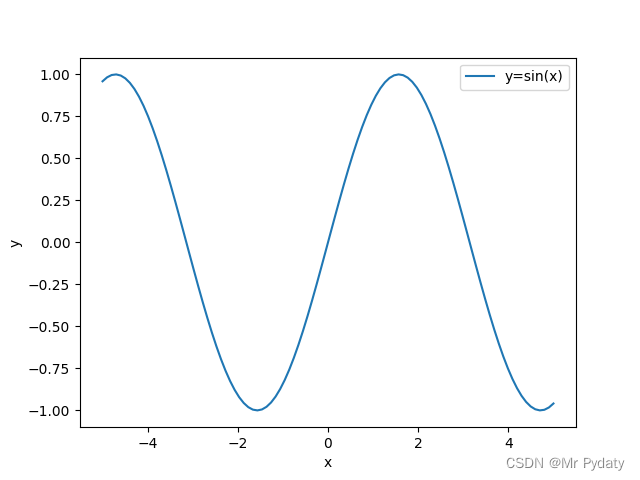
函数图像化
函数图像化 在进行模型提取时,往往会需要选择拟合的函数,因此,了解函数的图像对于模型拟合提取有益,以下是常见的一些函数的曲线 1 二次函数 常见的耳二次函数曲线,转换x与y数量级差异仅一个数量级, 2 三…...
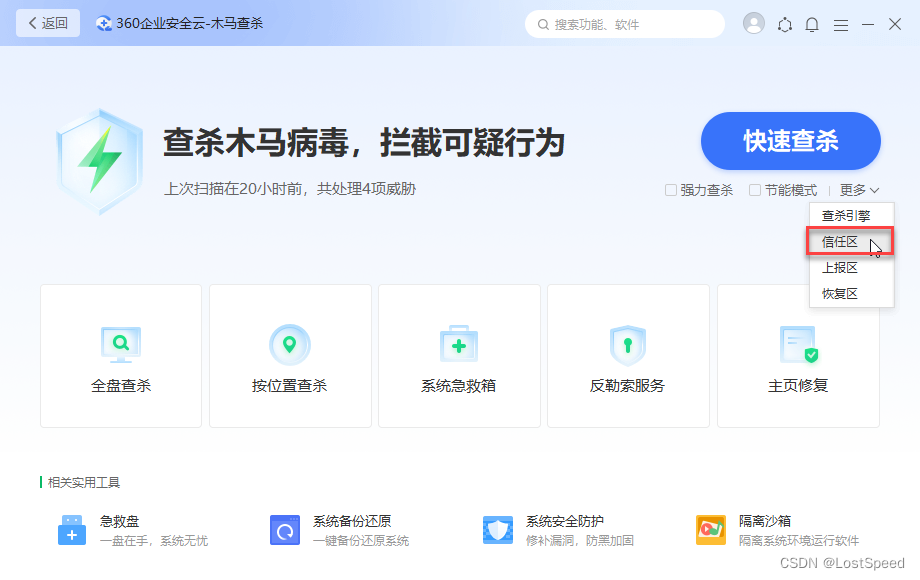
gnu工程的编译 - 以libiconv为例
文章目录 gnu工程的编译 - 以libiconv为例概述gnu官方源码包的发布版从官方的代码库直接迁出的git版源码如果安装了360, 需要添加开发相关的目录到信任区生成 configrue 的方法备注END gnu工程的编译 - 以libiconv为例 概述 gnu工程的下载分2种: gnu官方源码包的发布版 这种…...

在 CentOS 7.8 上安装 Node.js
1.安装 NVM(Node Version Manager): curl -o- https://raw.githubusercontent.com/nvm-sh/nvm/v0.39.1/install.sh | bash这将从 NVM 的 GitHub 仓库下载安装脚本并执行。请注意,您需要重新启动终端或者执行 source ~/.bashrc 以…...

【数据分析实战】冰雪大世界携程景区评价信息情感分析采集词云
文章目录 引言数据采集数据集展示数据预处理 数据分析评价总体情况分析本人浅薄分析 各游客人群占比分析本人浅薄分析 各评分雷达图本人浅薄分析 差评词云-可视化本人浅薄分析 好评词云-可视化本人浅薄分析 综合分析写在最后 今年冬天,哈尔滨冰雪旅游"杀疯了&q…...
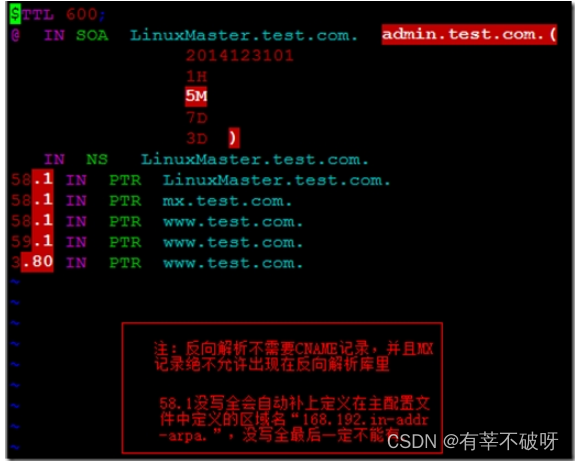
BIND-DNS配置介绍
一、主要配置文件 /etc/named.conf options { //Option 段全部配置 listen-on port 53 { 127.0.0.1; };//表示BIND将在53端口监听,若需要对所有IP进行监听,则修改为// listen-on port 53 { any; }; directory "/var/named"…...

Python技巧
Python,现如今非常热门的一种编程语言,在人工智能中大放异彩。做任何事都需要技巧,这可以大大提高效率,学习Python,同样如此! 第一个就是assret语句,让我们看下面一个关于折扣的例子: def dic…...
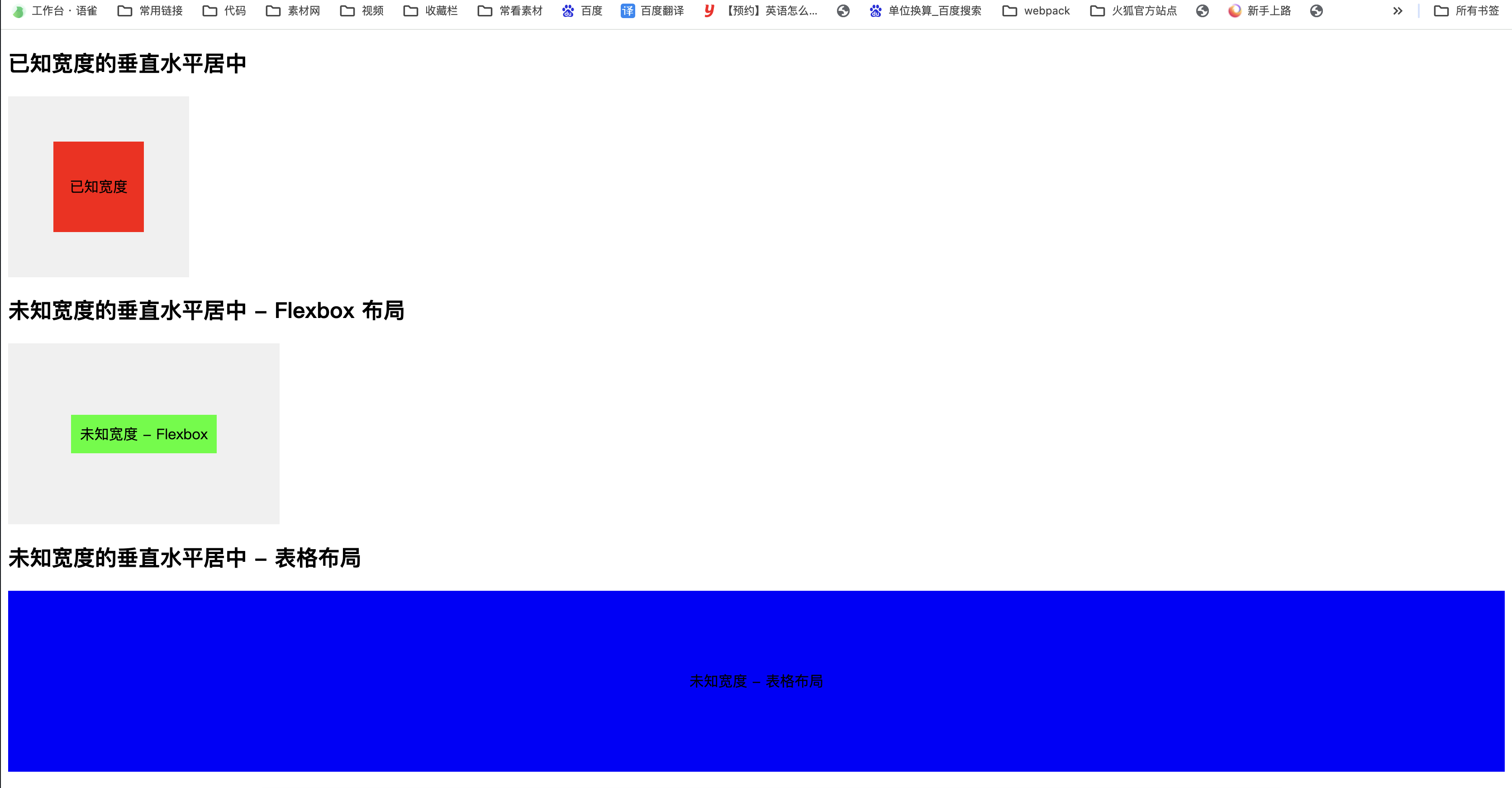
几种常见的CSS三栏布局?介绍下粘性布局(sticky)?自适应布局?左边宽度固定,右边自适应?两种以上方式实现已知或者未知宽度的垂直水平居中?
几种常见的CSS三栏布局 流体布局 效果: 参考代码: <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1…...

箭头函数 - JavaScript的新宠儿
📢 鸿蒙专栏:想学鸿蒙的,冲 📢 C语言专栏:想学C语言的,冲 📢 VUE专栏:想学VUE的,冲这里 📢 CSS专栏:想学CSS的,冲这里 Ǵ…...
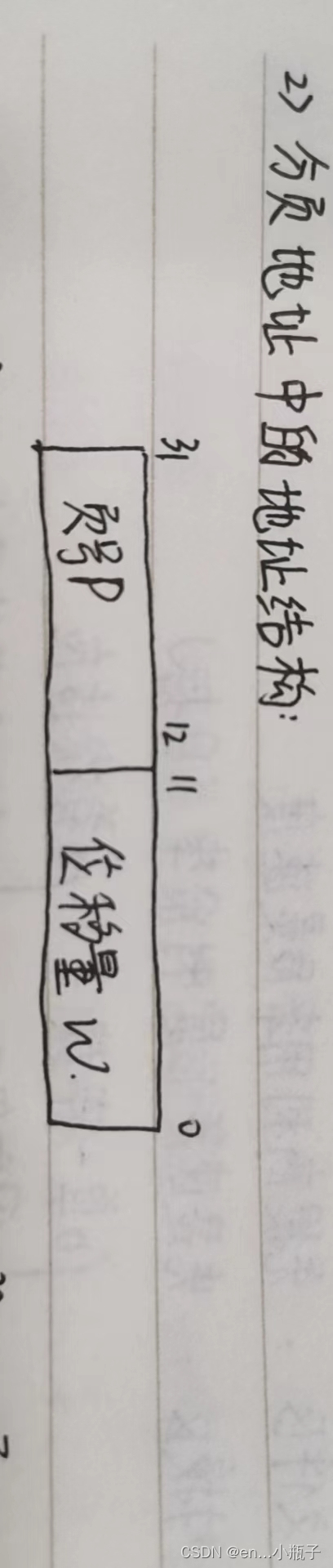
操作系统期末复习知识点
目录 一.概论 1.操作系统的介绍 2.特性 3.主要功能 4.作用 二.进程的描述与控制 1.进程的定义 2.特性 3.进程的创建步骤 4.基本状态转化 5.PCB的作用 6.进程与线程的比较 三.进程同步 1.同步的概念(挺重要的) 2.临界区 3.管程和进程的区…...

[英语学习][23][Word Power Made Easy]的精读与翻译优化
[序言] 译者的这次翻译, 完全直译, 生硬无比. [英文学习的目标] 提升自身的英语水平, 对日后编程技能的提升有很大帮助. 希望大家这次能学到东西, 同时加入我的社区讨论与交流英语相关的内容. [原著英文与翻译版对照][第22页] Knowledge is chiefly in the form of words…...

吉林大学19、21级计算机学院《计算机网络》期末真题试题
一、21级(考后回忆) 一、不定项选择(一共10个选择题,一个两分,选全得满分) 不定项:可以选择1~4个 考点有: ①协议、服务 ②码分多路复用通过接受码片序列,求哪个站点发送…...

python练习3【题解///考点列出///错题改正】
一、单选题 1.【单选题】 ——可迭代对象 下列哪个选项是可迭代对象( D)? A.(1,2,3,4,5) B.[2,3,4,5,6] C.{a:3,b:5} D.以上全部 知识点补充——【可迭代对象】 可迭代对象(iterable)是指可以通过迭代ÿ…...

LINUX服务器防火墙nf_conntrack问题一例
一、故障现象 业务反馈服务异常,无法响应请求,从系统日志 dmesg 或 /var/log/messages 看到大量以下记录:kernel: nf_conntrack: table full, dropping packet. 二、问题分析 业务高峰期服务器访问量大,内核 netfilter 模块 conntrack 相关参…...
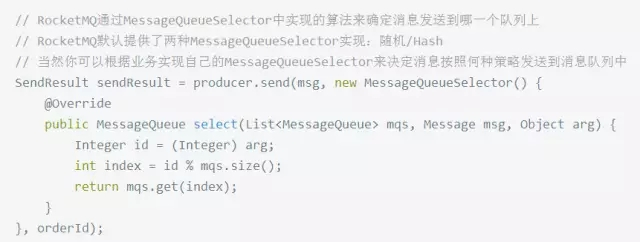
经典八股文之RocketMQ
核心概念 NameServer nameserver是整个rocketmq的大脑,是rocketmq的注册中心。broker在启动时向所有nameserver注册。生产者在发送消息之前先从 NameServer 获取 Broker 服务器地址列表(消费者一 样),然后根据负载均衡算法从列表中选择一台服务器进行消…...

Pandas之从sql库中导入数据的几种方法分析
1.使用mysql-connector-python库将SQL文件导入到Python中,并查询数据库中的表 确保已经安装mysql-connector-python库 #导入模块 import mysql.connector# 建立与MySQL数据库的连接 conn mysql.connector.connect(host"localhost",user"username&…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...
