KNN 回归
K 近邻回归(K-Nearest Neighbors Regression)是一种基于实例的回归算法,用于预测连续数值型的输出变量。它的基本思想是通过找到与给定测试样本最近的 K 个训练样本,并使用它们的输出值来预测测试样本的输出。它与 K 最近邻分类类似,但是用于解决回归问题而不是分类问题。
K 近邻回归算法的基本步骤:
- 数据准备:首先,我们需要准备训练集和测试集的特征数据和对应的目标变量。特征数据可以包括数值型、分类型或二元型的特征。目标变量是我们要预测的连续数值。
- 选择 K 值和距离度量方法:K 值是指选择的最近邻居的数量,通常通过交叉验证等方法来选择最优的 K 值。距离度量方法用于计算样本之间的距离,常见的方法有欧氏距离、曼哈顿距离等。
- 计算距离:对于给定的测试样本,我们计算它与训练集中所有样本的距离。距离的计算方法取决于选择的距离度量方法。
- 选择最近的 K 个邻居:根据距离的计算结果,选择与测试样本最近的 K 个训练样本作为邻居。可以使用排序算法(如快速排序)来加快寻找最近邻居的过程。
- 预测输出:对于回归问题,根据这 K 个邻居的输出值,可以采用平均值或加权平均值作为预测输出。通常,距离较近的邻居会被赋予更高的权重。
- 模型评估:使用回归评估指标(如均方误差、平均绝对误差等)来评估模型的性能。可以使用交叉验证等方法来获取更准确的模型评估结果。
需要注意的是,K 值的选择对算法的性能有重要影响。较小的 K 值会导致模型过拟合,而较大的 K 值可能会导致模型欠拟合。因此,通常需要通过交叉验证等方法来选择最优的 K 值。
K 近邻回归算法的基本思想就是,在给定一个新的数据点,它的输出值由其 K 个最近邻数据点的输出值的平均值(或加权平均值)来预测。
简单地说,KNN 回归使用多个近邻(即 k > 1)时,预测结果为这些邻居的对应目标值的平均值。
KNN 回归也可以用 score 方法进行模型评估,返回的是 R 2 R^2 R2 分数。 R 2 R^2 R2(R-squared)分数也叫做决定系数,是用来评估模型拟合优度的指标,它表示因变量的方差能够被自变量解释的比例。 R 2 R^2 R2 的取值范围在 0 到 1 之间,越接近 1 表示模型对数据的拟合越好,即模型能够解释更多的因变量的方差。当 R 2 R^2 R2 接近 0 时,说明模型无法解释因变量的方差,拟合效果较差。简单地说, R 2 = 1 R^2 = 1 R2=1 对应完美预测, R 2 = 0 R^2 = 0 R2=0 对应常数模型,即总是预测训练集响应(y_train)的平均值。
R 2 = 1 − ( S S R / S S T ) = 1 − ∑ i = 1 n ( y i − y i ′ ) 2 ∑ i = 1 n ( y i − y m e a n ) 2 R^2 = 1 - (SSR / SST) = 1 - \frac{\displaystyle\sum_{i=1}^{n}(y_i - y'_i)^2}{\displaystyle\sum_{i=1}^{n}(y_i - y_{mean})^2} R2=1−(SSR/SST)=1−i=1∑n(yi−ymean)2i=1∑n(yi−yi′)2
其中, y y y 为实际观测值, y ′ y' y′ 为预测值, y m e a n y_{mean} ymean 为实际观测值的均值。
SSR 与 SST:
- SSR(Sum of Squares Residual)为残差平方和,表示模型预测值与实际观测值之间的差异。
- SST(Total Sum of Squares)为总平方和,表示实际观测值的方差。
一般来说,KNN 分类器有 2 个重要参数:邻居个数以及数据点之间距离的度量方法。在实践中,使用较小的邻居个数(比如 3 个或 5 个)往往可以得到较好的结果,但在不同问题中应根据具体情况调节这个参数。数据点之间的距离度量方法默认使用欧式距离,它在许多情况下的效果都很好。
如果训练集很大(特征数很多或样本数很大),KNN 模型的预测速度可能会比较慢。
使用 KNN 算法时,对数据进行预处理是很重要的。
这一算法对于有很多特征(几百或更多)的数据集往往效果不好,对于大多数特征的大多数取值都为 0 的数据集(所谓的稀疏数据集)来说,这一算法的效果尤其不好。
在 sklearn 中调用 KNN 回归模型:
from sklearn.neighbors import KNeighborsRegressorreg = KNeighborsRegressor(n_neighbors=3)
reg.fit(X_train, y_train)
y_pred = reg.predict(X_new)
相关文章:

KNN 回归
K 近邻回归(K-Nearest Neighbors Regression)是一种基于实例的回归算法,用于预测连续数值型的输出变量。它的基本思想是通过找到与给定测试样本最近的 K 个训练样本,并使用它们的输出值来预测测试样本的输出。它与 K 最近邻分类类…...
Kali Linux——获取root权限
目录 一、设置root密码 【操作命令】 【操作实例】 二、临时获取root权限 【操作命令】 【操作实例】 三、提升用户到root 1、获取root权限 2、进入/etc/passwd 3、查看root账号ID 4、找到需要修改的用户 5、输入i,进入编辑模式 6、把用户的ID改成跟r…...

听GPT 讲Rust源代码--compiler(28)
File: rust/compiler/rustc_codegen_llvm/src/llvm/mod.rs 文件rust/compiler/rustc_codegen_llvm/src/llvm/mod.rs是Rust编译器的LLVM代码生成模块的一个文件。该文件定义了一些用于与LLVM交互的结构体、枚举和常量。 此文件的主要作用是: 定义编译器和LLVM之间的接…...

Debezium日常分享系列之:Debezium2.5版本之connector for JDBC
Debezium日常分享系列之:Debezium2.5版本之connector for JDBC 一、概述二、JDBC 连接器的工作原理三、使用复杂的 Debezium 变更事件四、至少一次交付五、多项任务六、数据和列类型映射七、主键处理八、删除模式九、幂等写入十、Schema evolution十一、引用和区分大…...
爬虫网易易盾滑块案例:某乎
声明: 该文章为学习使用,严禁用于商业用途和非法用途,违者后果自负,由此产生的一切后果均与作者无关 一、滑块初步分析 js运行 atob(‘aHR0cHM6Ly93d3cuemhpaHUuY29tL3NpZ25pbg’) 拿到网址,浏览器打开网站࿰…...
机器学习笔记 - 偏最小二乘回归 (PLSR)
一、偏最小二乘回归:简介 PLS 方法构成了一个非常大的方法族。虽然回归方法可能是最流行的 PLS 技术,但它绝不是唯一的一种。即使在 PLSR 中,也有多种不同的算法可以获得解决方案。PLS 回归主要由斯堪的纳维亚化学计量学家 Svante Wold 和 Harald Martens 在 20 世纪 80 年代…...
【HTML5】第1章 HTML5入门
学习目标 了解网页基本概念,能够说出网页的构成以及网页相关名词的含义 熟悉Web标准,能够归纳Web标准的构成。 了解浏览器,能够说出各主流浏览器的特点。 了解HTML5技术,能够知道HTML5发展历程、优势以及浏览器对HTML5的支持情…...

dyld: Library not loaded: /usr/lib/swift/libswiftCoreGraphics.dylib
更新Xcode14后低版本iPhone调试报错 dyld: Library not loaded: /usr/lib/swift/libswiftCoreGraphics.dylib Referenced from: /var/containers/Bundle/Application/…/….app/… Reason: image not found 这是缺少libswiftCoreGraphics库 直接导入libswiftCoreGraphics库即…...

React Hooks中useState的介绍,并封装为useSetState函数的使用
useState 允许我们定义状态变量,并确保当这些状态变量的值发生变化时,页面会重新渲染。 useState 返回值 const [state, setState] useState(initialState);useState 返回一个长度为 2 的数组。通常,我们这样定义状态变量: co…...
)
5 个最适合SEI 网络空投交易等操作的钱包(Bitget Wallet,Coin98等)
大家好!Sei 网络比 SOL 快 5 倍,手续费低,还能防止前台交易。好了,我不会占用大家太多时间,让我们直奔主题吧。 Sei 官方:推特(twitter.com/SeiNetwork) 如上图所示,目前…...
.net8 AOT编绎-跨平台调用C#类库的新方法-函数导出
VB.NET AOT无法编绎DLL,微软的无能,正是你的机会 .net8 AOT编绎-跨平台调用C#类库的新方法-函数导出 1,C#命令行创建工程:dotnet new classlib -o CSharpDllExport 2,编写一个静态方法,并且为它打上UnmanagedCallersO…...

第三十八周周报:文献阅读 +BILSTM+GRU+Seq2seq
目录 摘要 Abstract 文献阅读:耦合时间和非时间序列模型模拟城市洪涝区洪水深度 现有问题 提出方法 创新点 XGBoost和LSTM耦合模型 XGBoost算法 编辑 LSTM(长短期记忆网络) 耦合模型 研究实验 数据集 评估指标 研究目的 洪…...

天津最新web前端培训班 如何提升web技能?
随着互联网的迅猛发展,web前端成为了一个热门的职业方向。越来越多的人希望能够通过学习web前端技术来提升自己的就业竞争力。为了满足市场的需求,许多培训机构纷纷推出了web前端培训课程。 什么是WEB前端 web前端就是web给用户展示的东西,…...

Linux下QT生成的(.o)、(.a)、(.so)、(.so.1)、(.so.1.0)、(.so.1.0.0)之间的区别
记录一下遇到的问题:Linux系统下Qt编译第三方动态库会生成多个.so文件,不了解的小伙伴可能很疑惑: (1)Linux 下 QT 生成的(.o)、(.a)和(.so)三个文…...

线性代数 --- 为什么LU分解中L矩阵的行列式一定等于正负1?
以下是关于下三角矩阵L的行列式一定等于-1的一些说明 笔者的一些话(写在最前面): 这是一篇小文,是我写的关于求解矩阵行列式的一篇文章中的一部分。之所以把这一段专门提溜出来,是因为这一段相对于原文是可以完全独立的,也是因为我…...
Redisson 源码解析 - 分布式锁实现过程
一、Redisson 分布式锁源码解析 Redisson是架设在Redis基础上的一个Java驻内存数据网格。在基于NIO的Netty框架上,充分的利用了Redis键值数据库提供的一系列优势,在Java实用工具包中常用接口的基础上,为使用者提供了一系列具有分布式特性的常…...
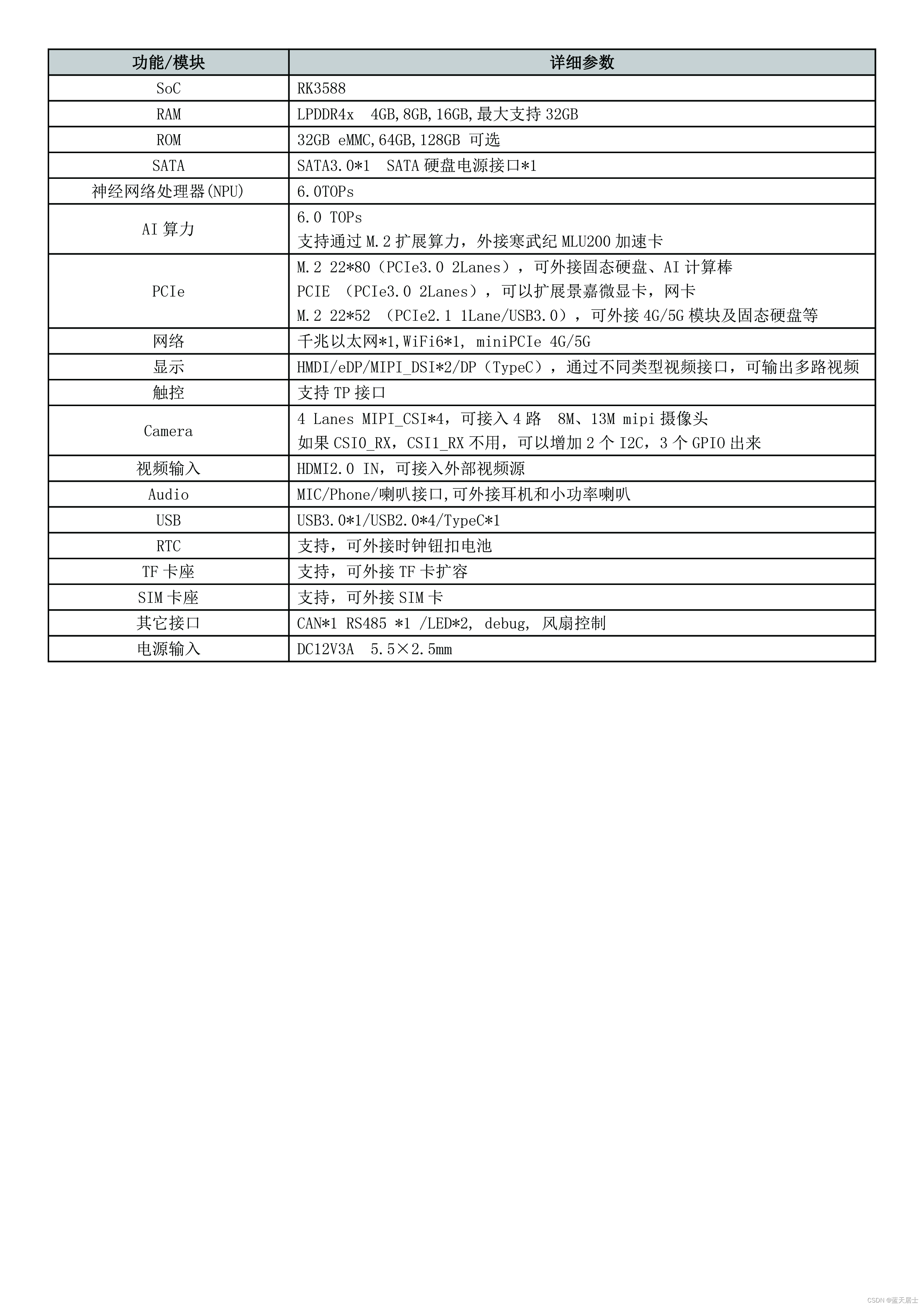
玩转贝启科技BQ3588C开源鸿蒙系统开发板 —— 开发板详情与规格
本文主要参考: BQ3588C_开发板详情-开源鸿蒙技术交流-Bearkey-开源社区 BQ3588C_开发板规格-开源鸿蒙技术交流-Bearkey-开源社区 厦门贝启科技有限公司-Bearkey-官网 1. 开发板详情 RK3588 核心板是一款由贝启科技自主研发的基于瑞芯微 RK3588 AI 芯片的智能核心…...
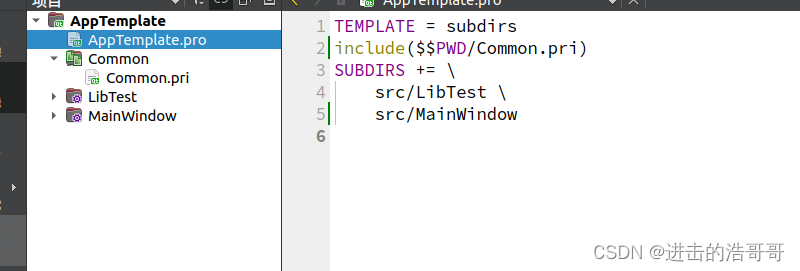
Qt pro文件
1. 项目通常结构 2.pri文件 pri文件可定义通用的宏,例如创建一个COMMON.pri文件内容为 COMMON_PATH D:\MyData 然后其它pri或者pro文件如APPTemplate.pro文件中通过添加include(Common.pri) ,QtCreator就会自动在项目结构树里面创建对应的节点 3.变量…...
实验笔记之——服务器链接
最近需要做NeRF相关的开发,需要用到GPU,本博文记录本人配置服务器远程链接的过程,本博文仅供本人学习记录用~ 连上服务器 首先先确保环境是HKU的网络环境(HKU AnyConnect也可)。伙伴已经帮忙创建好用户(第一次登录会提示重新设置密码)。用cmd ssh链接ssh -p 60001 <u…...
微服务-java spi 与 dubbo spi
Java SPI 通过一个案例来看SPI public interface DemoSPI {void echo(); } public class FirstImpl implements DemoSPI{Overridepublic void echo() {System.out.println("first echo");} } public class SecondImpl implements DemoSPI{Overridepublic void ech…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...
