C++力扣题目111--二叉树的最小深度
力扣题目链接(opens new window)
给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
说明: 叶子节点是指没有子节点的节点。
示例:
给定二叉树 [3,9,20,null,null,15,7],

返回它的最小深度 2
思路
看完了这篇104.二叉树的最大深度 (opens new window),再来看看如何求最小深度。
直觉上好像和求最大深度差不多,其实还是差不少的。
本题依然是前序遍历和后序遍历都可以,前序求的是深度,后序求的是高度。
- 二叉树节点的深度:指从根节点到该节点的最长简单路径边的条数或者节点数(取决于深度从0开始还是从1开始)
- 二叉树节点的高度:指从该节点到叶子节点的最长简单路径边的条数后者节点数(取决于高度从0开始还是从1开始)
那么使用后序遍历,其实求的是根节点到叶子节点的最小距离,就是求高度的过程,不过这个最小距离 也同样是最小深度。
以下讲解中遍历顺序上依然采用后序遍历(因为要比较递归返回之后的结果,本文我也给出前序遍历的写法)。
本题还有一个误区,在处理节点的过程中,最大深度很容易理解,最小深度就不那么好理解,如图:

这就重新审题了,题目中说的是:最小深度是从根节点到最近叶子节点的最短路径上的节点数量。,注意是叶子节点。
什么是叶子节点,左右孩子都为空的节点才是叶子节点!
#递归法
来来来,一起递归三部曲:
- 确定递归函数的参数和返回值
参数为要传入的二叉树根节点,返回的是int类型的深度。
代码如下:
int getDepth(TreeNode* node)
- 确定终止条件
终止条件也是遇到空节点返回0,表示当前节点的高度为0。
代码如下:
if (node == NULL) return 0;
- 确定单层递归的逻辑
这块和求最大深度可就不一样了,一些同学可能会写如下代码:
int leftDepth = getDepth(node->left);
int rightDepth = getDepth(node->right);
int result = 1 + min(leftDepth, rightDepth);
return result;
这个代码就犯了此图中的误区:
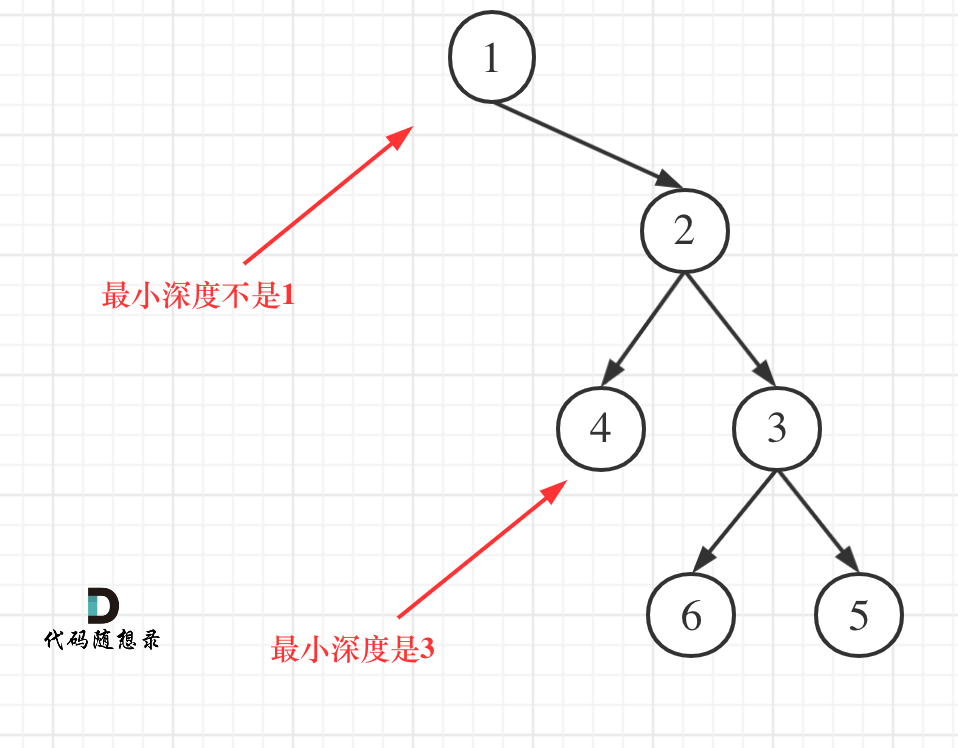
如果这么求的话,没有左孩子的分支会算为最短深度。
所以,如果左子树为空,右子树不为空,说明最小深度是 1 + 右子树的深度。
反之,右子树为空,左子树不为空,最小深度是 1 + 左子树的深度。 最后如果左右子树都不为空,返回左右子树深度最小值 + 1 。
代码如下:
int leftDepth = getDepth(node->left); // 左
int rightDepth = getDepth(node->right); // 右// 中
// 当一个左子树为空,右不为空,这时并不是最低点
if (node->left == NULL && node->right != NULL) { return 1 + rightDepth;
}
// 当一个右子树为空,左不为空,这时并不是最低点
if (node->left != NULL && node->right == NULL) { return 1 + leftDepth;
}
int result = 1 + min(leftDepth, rightDepth);
return result;
遍历的顺序为后序(左右中),可以看出:求二叉树的最小深度和求二叉树的最大深度的差别主要在于处理左右孩子不为空的逻辑。
整体递归代码如下:
class Solution {
public:int getDepth(TreeNode* node) {if (node == NULL) return 0;int leftDepth = getDepth(node->left); // 左int rightDepth = getDepth(node->right); // 右// 中// 当一个左子树为空,右不为空,这时并不是最低点if (node->left == NULL && node->right != NULL) { return 1 + rightDepth;} // 当一个右子树为空,左不为空,这时并不是最低点if (node->left != NULL && node->right == NULL) { return 1 + leftDepth;}int result = 1 + min(leftDepth, rightDepth);return result;}int minDepth(TreeNode* root) {return getDepth(root);}
};
精简之后代码如下:
class Solution {
public:int minDepth(TreeNode* root) {if (root == NULL) return 0;if (root->left == NULL && root->right != NULL) {return 1 + minDepth(root->right);}if (root->left != NULL && root->right == NULL) {return 1 + minDepth(root->left);}return 1 + min(minDepth(root->left), minDepth(root->right));}
};
精简之后的代码根本看不出是哪种遍历方式,所以依然还要强调一波:如果对二叉树的操作还不熟练,尽量不要直接照着精简代码来学。
前序遍历的方式:
class Solution {
private:int result;void getdepth(TreeNode* node, int depth) {// 函数递归终止条件if (node == nullptr) {return;}// 中,处理逻辑:判断是不是叶子结点if (node -> left == nullptr && node->right == nullptr) {result = min(result, depth);}if (node->left) { // 左getdepth(node->left, depth + 1);}if (node->right) { // 右getdepth(node->right, depth + 1);}return ;}public:int minDepth(TreeNode* root) {if (root == nullptr) {return 0;}result = INT_MAX;getdepth(root, 1);return result;}
};
#迭代法
相对于104.二叉树的最大深度 (opens new window),本题还可以使用层序遍历的方式来解决,思路是一样的。
如果对层序遍历还不清楚的话,可以看这篇:二叉树:层序遍历登场!(opens new window)
需要注意的是,只有当左右孩子都为空的时候,才说明遍历到最低点了。如果其中一个孩子不为空则不是最低点
代码如下:(详细注释)
class Solution {
public:int minDepth(TreeNode* root) {if (root == NULL) return 0;int depth = 0;queue<TreeNode*> que;que.push(root);while(!que.empty()) {int size = que.size();depth++; // 记录最小深度for (int i = 0; i < size; i++) {TreeNode* node = que.front();que.pop();if (node->left) que.push(node->left);if (node->right) que.push(node->right);if (!node->left && !node->right) { // 当左右孩子都为空的时候,说明是最低点的一层了,退出return depth;}}}return depth;}
};相关文章:

C++力扣题目111--二叉树的最小深度
力扣题目链接(opens new window) 给定一个二叉树,找出其最小深度。 最小深度是从根节点到最近叶子节点的最短路径上的节点数量。 说明: 叶子节点是指没有子节点的节点。 示例: 给定二叉树 [3,9,20,null,null,15,7], 返回它的最小深度 2 思路 看完了这篇104.二…...
)
【图像拼接】源码精读:Adaptive As-Natural-As-Possible Image Stitching(AANAP/ANAP)
第一次来请先看这篇文章:【图像拼接(Image Stitching)】关于【图像拼接论文源码精读】专栏的相关说明,包含专栏内文章结构说明、源码阅读顺序、培养代码能力、如何创新等(不定期更新) 【图像拼接论文源码精读】专栏文章目录 【源码精读】As-Projective-As-Possible Imag…...
解决docker run报错:Error response from daemon: No command specified.
将docker镜像export/import之后,对新的镜像执行docker run时报错: docker: Error response from daemon: No command specified. 解决方法: 方案1: 查看容器的command: docker ps --no-trunc 在docker run命令上增加…...

算法第十二天-最大整除子集
最大整除子集 题目要求 解题思路 来自[宫水三叶] 根据题意:对于符合要求的[整除子集]中的任意两个值,必然满足[较大数]是[较小数]的倍数 数据范围是 1 0 3 10^3 103,我们不可能采取获取所有子集,再检查子集是否合法的暴力搜解法…...

简单易懂的PyTorch 损失函数:优化机器学习模型的关键
目录 torch.nn子模块Loss Functions详解 nn.L1Loss 用途 用法 使用技巧 注意事项 代码示例 nn.MSELoss 用途 用法 使用技巧 注意事项 代码示例 nn.CrossEntropyLoss 用途 用法 使用技巧 注意事项 代码示例 使用类别索引 使用类别概率 nn.CTCLoss 用途 …...

Kubernetes/k8s的存储卷/数据卷
k8s的存储卷/数据卷 容器内的目录和宿主机的目录挂载 容器在系统上的生命周期是短暂的,delete,k8s用控制创建的pod,delete相当于重启,容器的状态也会回复到初始状态 一旦回到初始状态,所有的后天编辑的文件都会消失…...
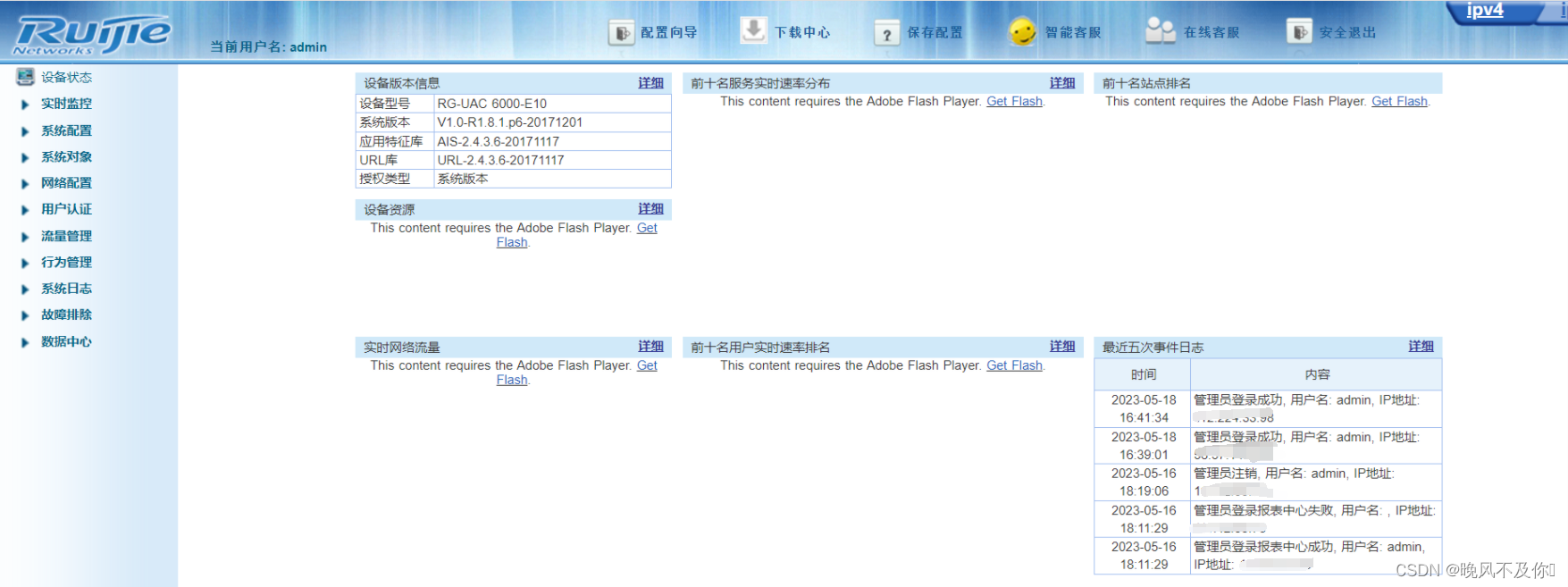
【漏洞复现】锐捷RG-UAC统一上网行为管理系统信息泄露漏洞
Nx01 产品简介 锐捷网络成立于2000年1月,原名实达网络,2003年更名,自成立以来,一直扎根行业,深入场景进行解决方案设计和创新,并利用云计算、SDN、移动互联、大数据、物联网、AI等新技术为各行业用户提供场…...
)
Android - 串口通讯(SerialPort)
最早的博客Android 模拟串口通信过程_launch virtual serial port driver pro-CSDN博客里就是用过 Google 提供的 demo,最近想再写个其他的demo发现用起来有点麻烦,还需要导入其他 module,因此在网上找到了Android-SerialPort-API: https://g…...

如何使用設置靜態住宅IP
靜態住宅IP就是一種靜態的、分配給住宅用戶的IP地址。與動態IP地址不同,靜態住宅IP一旦分配給用戶,就會一直保持不變,除非ISP(Internet Service Provider,互聯網服務提供商)進行手動更改。那麼,…...
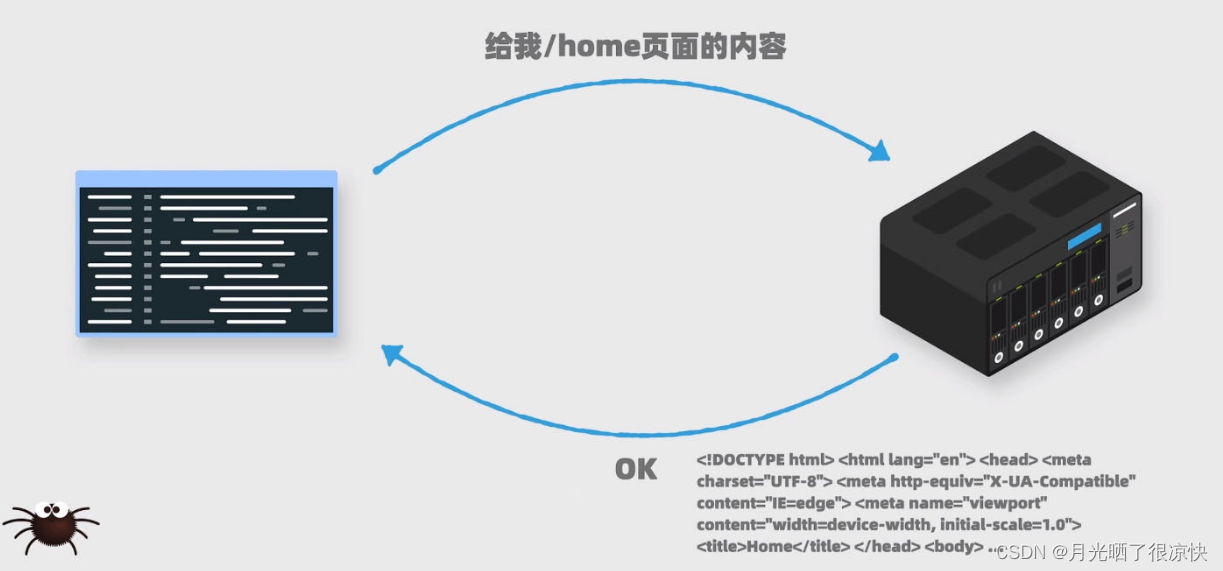
在学习爬虫前的准备
1. 写一个爬虫程序需要分几步 获取网页内容。 我们会通过代码给一个网站服务器发送请求,它会返回给我们网页上的内容。 在我们平时使用浏览器访问服务器内容是,本质上也是向服务器发送一个请求,然后服务器返回网页上的内容。只不过浏览器还会…...
windows下安装oracle-win-64-11g超详细图文步骤
官方下载地址:点这里 1.根据自己电脑情况,解压64或者32位客户端,以及database压缩包 2.解压后双击执行database文件夹下的setup.exe 3.详细的安装步骤 (1)数据库安装 一、配置安全更新 电子邮件可写可不写…...

Go模板后端渲染时vue单页面冲突处理
go后端模版语法是通过 {{}} ,vue也是通过双花括号来渲染的,如果使用go渲染vue的html页面的时候就会报错,因为分别不出来哪个是vue的,哪个是go的,既可以修改go的模板语法 template.New("output").Delims(&qu…...

笔记本摄像头模拟监控推送RTSP流
使用笔记本摄像头模拟监控推送RTSP流 一、基础安装软件准备 本文使用软件下载链接:下载地址 FFmpeg软件: Download ffmpeg 选择Windows builds by BtbN 一个完整的跨平台解决方案,用于录制、转换和流式传输音频和视频。 EasyDarwin软件:Download Easy…...

鸿蒙开发已解决-ArkTS编译时遇到arkts-no-obj-literals-as-types错误
文章目录 项目场景:问题描述原因分析:解决方案:解决方案1解决方案2此Bug解决方案总结项目场景: 在开发鸿蒙项目过程中,遇到了arkts-no-obj-literals-as-types,总结了自己和网上人的解决方案,故写下这篇文章。 遇到问题: rkTS编译时遇到arkts-no-obj-literals-as-type…...
实现目标检测中的数据格式自由(labelme json、voc、coco、yolo格式的相互转换)
在进行目标检测任务中,存在labelme json、voc、coco、yolo等格式。labelme json是由anylabeling、labelme等软件生成的标注格式、voc是通用目标检测框(mmdetection、paddledetection)所支持的格式,coco是通用目标检测框࿰…...

一文读懂JVS逻辑引擎如何调用规则引擎:含详细步骤与场景示例
在当今的数字化时代,业务逻辑和规则的复杂性不断增加,这使得逻辑引擎和规则引擎在处理业务需求时显得尤为重要。逻辑引擎和规则引擎通过定义、解析和管理业务逻辑和规则,能够帮助企业提高工作效率、降低运营成本,并增强决策的科学…...

苹果应用上架是否需要软件著作权?
苹果应用上架是否需要软件著作权? 摘要 随着移动互联网的发展,苹果应用在市场上占据了很大份额。但是,很多开发者在上传苹果应用到App Store时,都会遇到一个问题,即是否需要进行软著申请?本文将深入探讨这…...
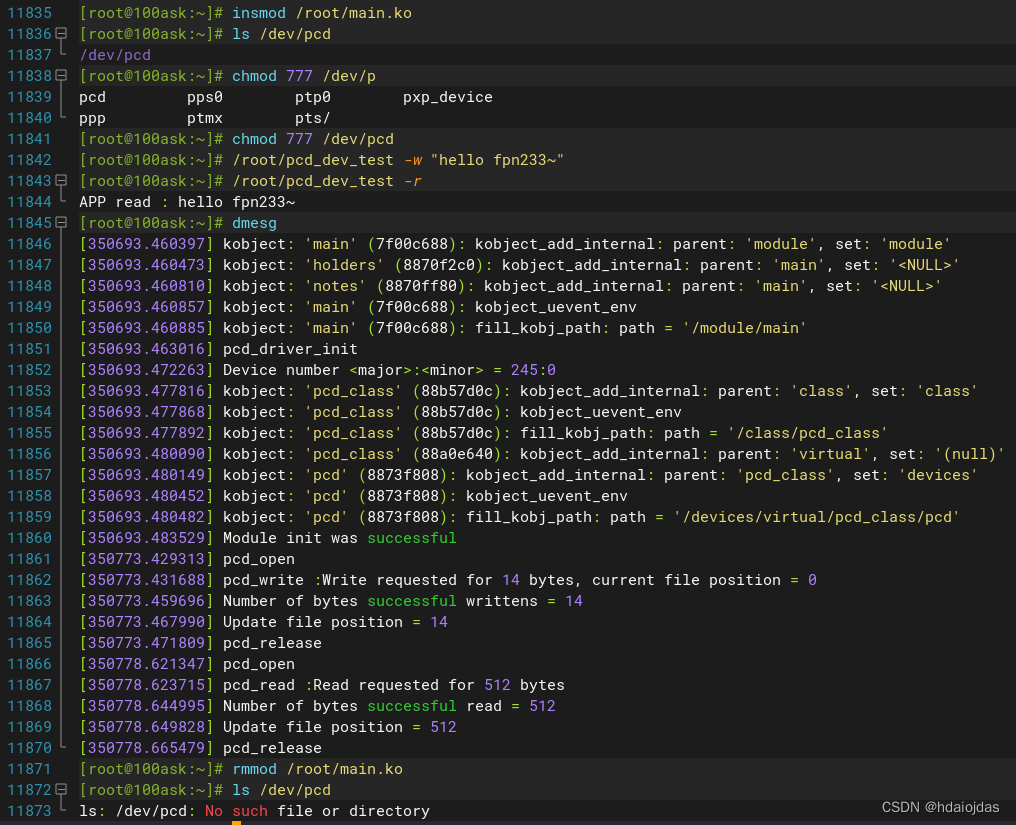
LDD学习笔记 -- Linux字符设备驱动
LDD学习笔记 -- Linux字符设备驱动 虚拟文件系统 VFS设备号相关Kernel APIs动态申请设备号动态创建设备文件内核空间和用户空间的数据交换系统调用方法readwritelseek 写一个伪字符设备驱动在主机上测试pcd(HOST)在目标板上测试pcd(TARGET) 字符驱动程序用于与Linux内核中的设备…...

杰理AC63串口收发实例
在event.h文件中预定义串口消息 #define DEVICE_EVENT_FROM_MY_UART ((M << 24) | (Y << 16) | (U << 8) | \0)在app_spp_and_le.c文件里对SYS_DEVICE_EVENT做处理,添加收到DEVICE_EVENT_FROM_MY_UART消息时的处理函数my_rx_handler(); cas…...
麦芯(MachCore)开发教程1 --- 设备软件中间件
黄国强 2024/1/10 acloud163.com 对任何公司来说,在短时间内开发一款高质量设备专用软件,是一件不太容易做到的事情。麦芯是笔者发明的一款设备软件中间件产品。麦芯致力于给设备厂商提供一个开发工具和平台,让客户快速高效的开发自己的设备专…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...
